Добавлен: 23.11.2023
Просмотров: 125
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
преобразователя расхода аммиака и расчет передаточной функции
САПФИР-22ДД-2440 предназначен для преобразования в унифицированный токовый сигнал разности расхода газа (аммиака).
Основные технические характеристики САПФИР-22ДД-2440:
Верхние пределы измерения, МПА 0,63.
Пределы допускаемого рабочего избыточного давления, кгс/см2 10.
Выходные сигналы, мА от 0 до 5.
Пределы допускаемой основной погрешности, % 0,5.
Входной сигнал датчика расхода газа - расход Q:
- изменяется в переделах ∆Q, м3/ч 0 ÷ 19.
Выходной сигнал – ток:
- изменяется в приделах, мА 0 ÷ 5.
Вывод передаточной функции:
Зависимость между выходным и измеряемым параметром определяется выражением:
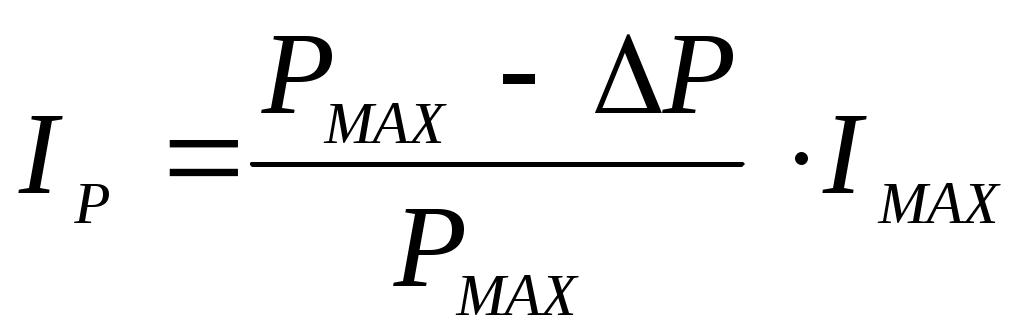 ,
,
где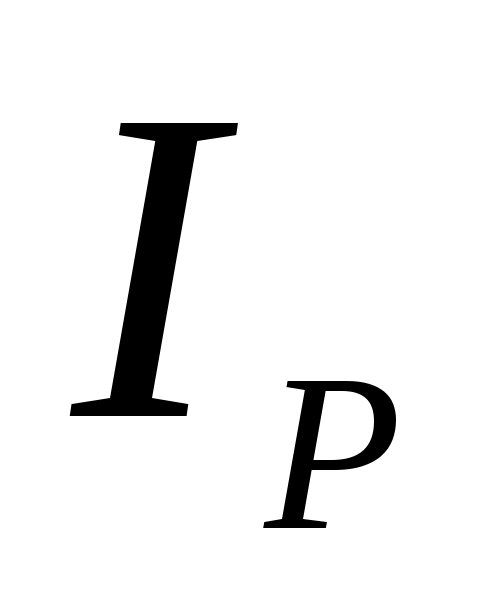 - расчетное значение выходного сигнала, соответствующее измеряемому давлению или разности давлений
- расчетное значение выходного сигнала, соответствующее измеряемому давлению или разности давлений 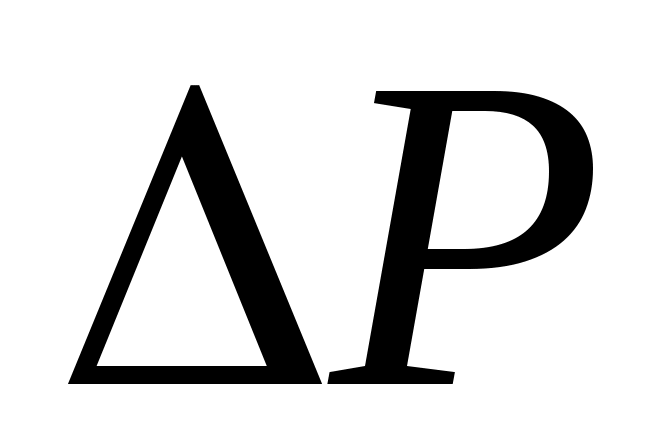 , мА;
, мА;
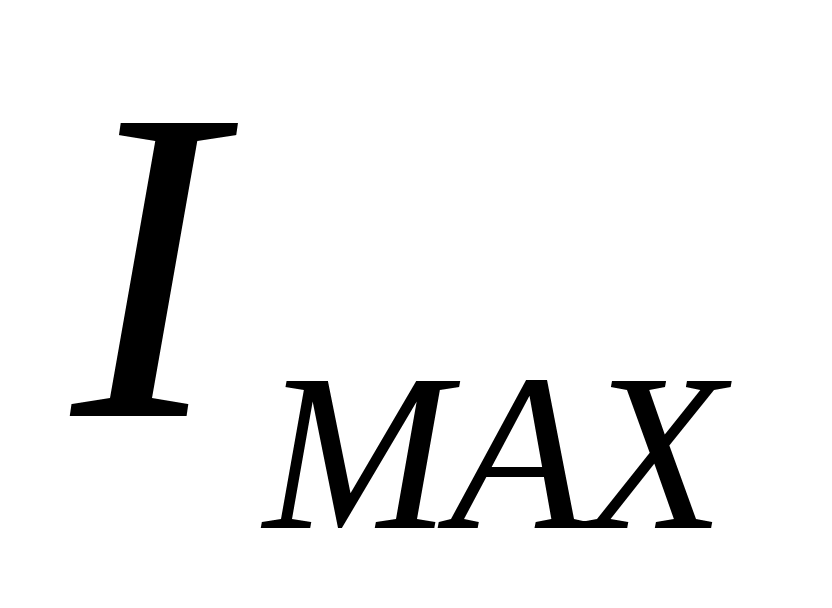 - наибольшее выходное значение выходного сигнала, (5 мА);
- наибольшее выходное значение выходного сигнала, (5 мА);
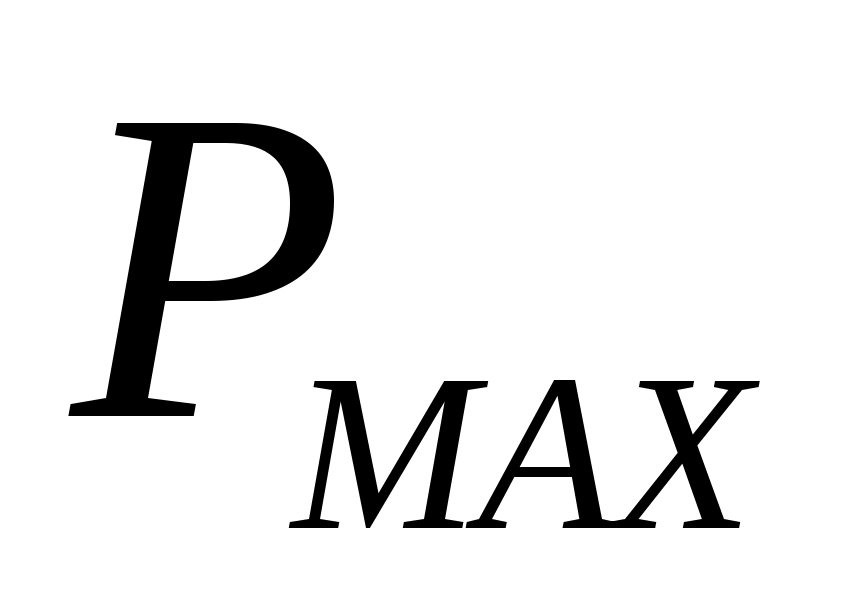 - верхний предел измерений измеряемого давления (разности давлений), МПа;
- верхний предел измерений измеряемого давления (разности давлений), МПа;
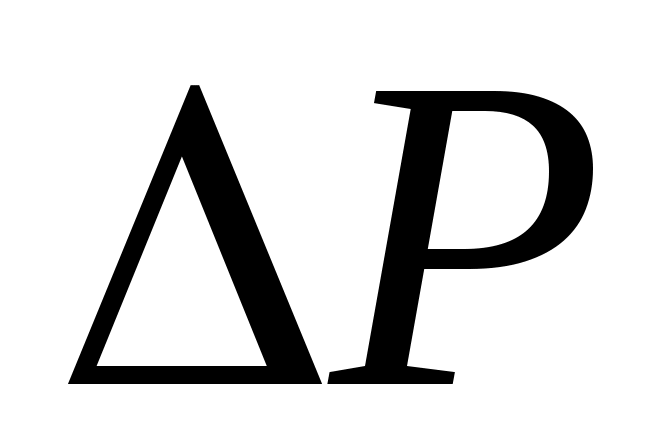 - значение измеряемого давления (разности давлений), (0,063 МПа).
- значение измеряемого давления (разности давлений), (0,063 МПа).
Зависимость между расходом Q и перепадом давления ΔP на диафрагме описывается выражением:
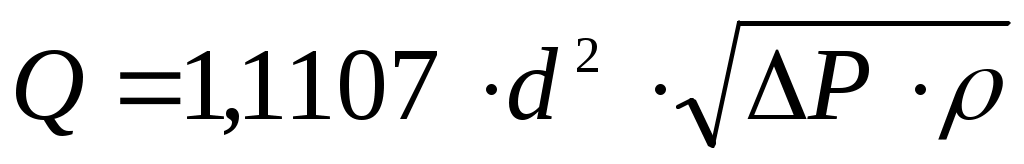 ,
,
где d – диаметр диафрагмы, м;
ρ – плотность рабочей среды (для аммиака ρ=7710), кг/м3.
Для диафрагмы диафрагмы камерной ДКС-6-200 условный проход составляет Ду 200 мм, внутренний диаметр составляет d=0,05 м. Таким образом при измеряемом расходе Q=19м3/ч=40,69кг/с перепад давления рассчитывается следующим образом
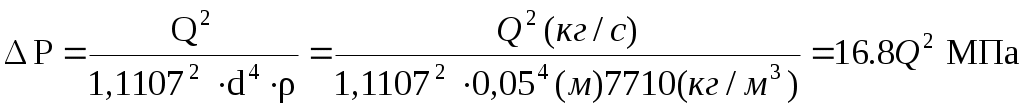
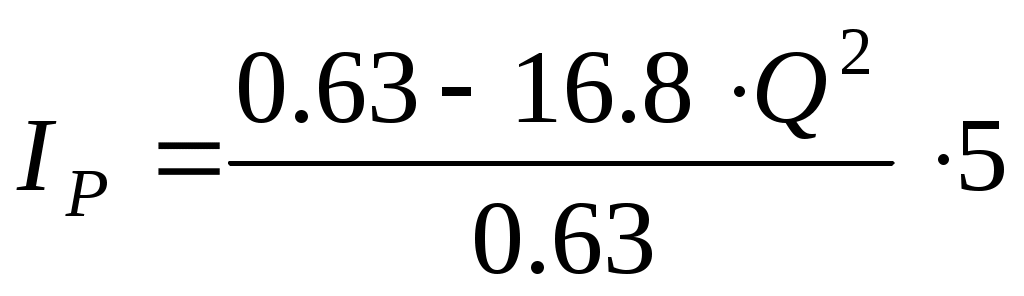
Построим по данному выражению характеристику
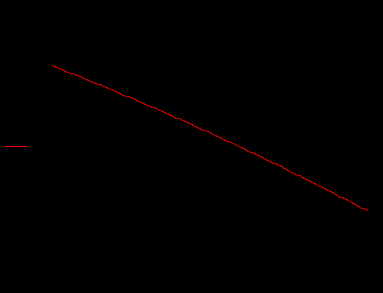
I(Q)
Q

Рисунок 19– Характеристика преобразователя расхода в рабочем диапазоне
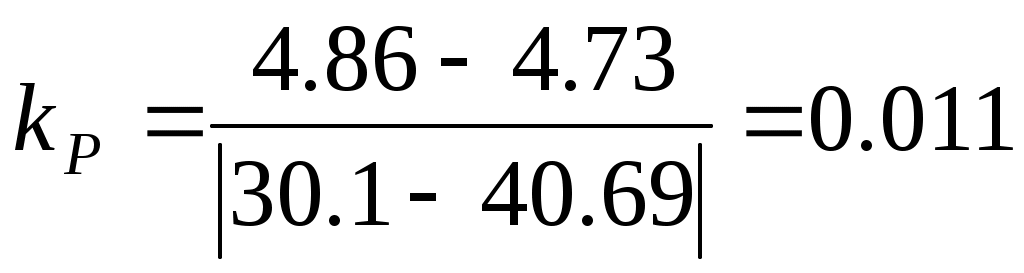 мА/(кг/с).
мА/(кг/с).
Или в системе СИ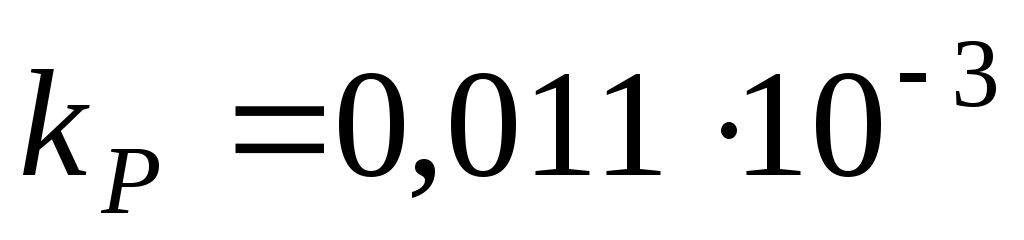 А/(кг/с).
А/(кг/с).
Таким образом, передаточную функцию датчика расхода можно представить в виде усилительного звена с рассчитанным выше коэффициентом пропорциональности.
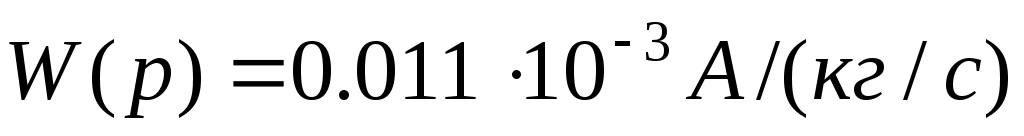 (19)
(19)
4.8 Выбор датчика рН пульпы и расчет передаточной функции
pH-метр — прибор для измерения концентрации ионов водорода (pH) в растворах и сырье, объектах окружающей среды и производственных систем непрерывного контроля технологических процессов.
Промышленный двухканальный рН-метр рН-4122 предназначен для автоматического измерения активности ионов водорода.

Рисунок 19 – Промышленный двухканальный рН-метр рН-4122
Прибор представляет собой двухканальное средство измерений и состоит из двух первичных преобразователей (ПП) рН-41211 и двухканального измерительного прибора (ИП).рН-4122 обеспечивает цифровую индикацию значений рН, преобразование их в пропорциональные значения унифицированных выходных сигналов постоянного тока, обмен данными по цифровому интерфейсу RS485, сигнализацию о выходе измеряемых параметров за пределы заданных значений.
Технические характеристики рН-метра рН-4122:
Время запаздывания, сек 60.
Количество измерительных каналов 2.
Диапазон измерений рН, ед. pH от 0 до 14.
Диапазон измерений ЭДС, мВ от минус 750 до плюс 750.
Температура анализируемой среды, ºС от 0 до плюс 100.
Предел допускаемого значения основной абсолютной погрешности:
- при измерении рН в комплекте с ЗС плюс минус 0,05.
- при измерении температуры плюс минус 0,5.
Тип индикатора жидкокристаллический графический.
Параметры сетевого питания, В, Гц 50.
Потребляемая мощность, Вт не более 15.
Входной сигнал рН-метра - ед. рН:
- изменяется в переделах, ед.рН 4 ÷ 5.
Выходной сигнал – ток:
- изменяется в приделах, мА 0 ÷ 5.
Передаточная функция:
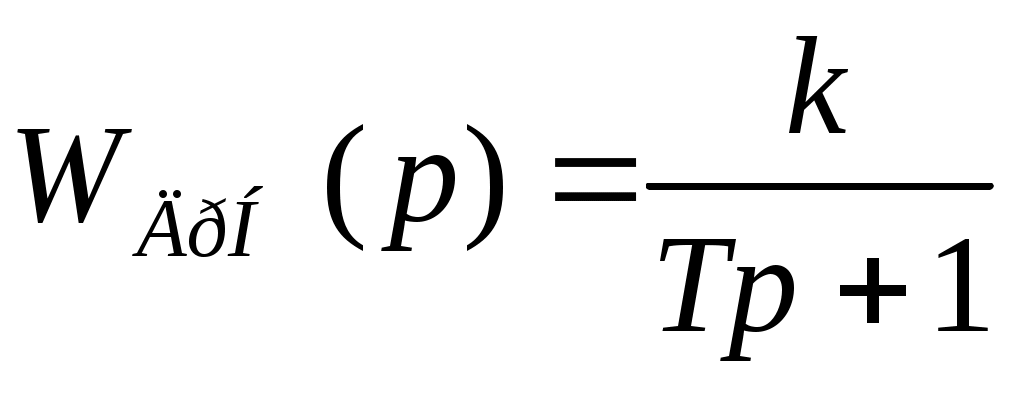 ,
,
где T – постоянная времени;
k – коэффициент преобразования.
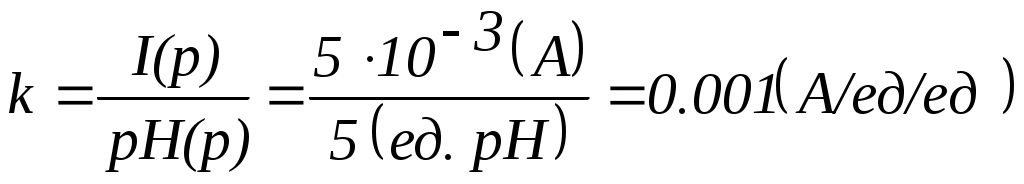
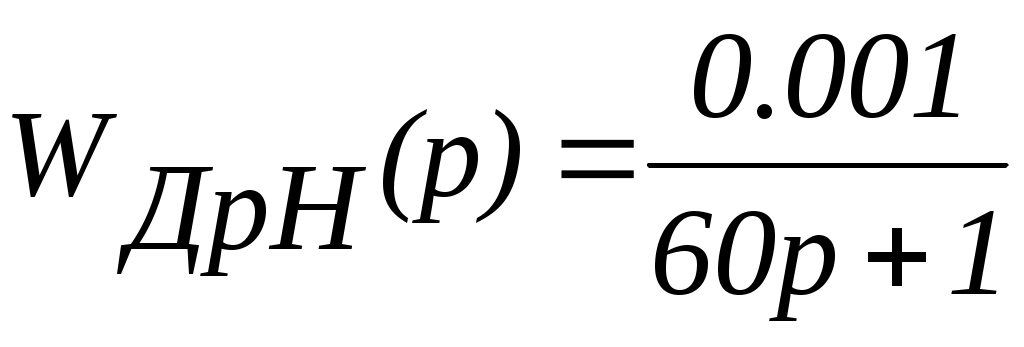 (20)
(20)
4.9 Выбор скоростного аммонизатора-испарителя и расчет передаточной функции
САИ представляет собой «участок смешения» и «перемешивания» представленный на рисунке.
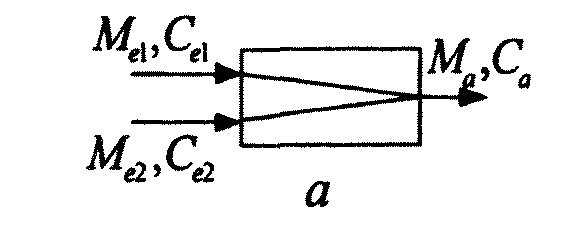

Me1- расход первого потока; Me2 – расход второго потока; Ma – поток полученный результате смешения
Рисунок 20 - Параметрическая схема двухкомпонентной системы
Технические характеристики САИ:
pH пульпы 4 ÷ 5.
Расход аммиака, кг/с 40,96.
Расход кислоты в САИ, кг/с 11,2.
Масса пульпы, кг, 10,1.
Диаметр САИ, мм 4020.
Высота, мм 9700.
Диаметр контура, мм 920.
Диаметр корпуса Dр , мм 200.
Диаметр патрубка ввода кислоты dк, мм 100.
Диаметр патрубка ввода аммиака dам, мм 125.
Диаметр сопла аммиака dсам, мм 100.
Диаметр сопла пульпы (на конце транспортной трубы) dп, мм 125.
Работа аммонизатора-испарителя основана на циркуляции потока кислоты и взаимодействии его с газообразным аммиаком и достаточно точно описываются дифференциальными уравнениями 1-го порядка с запаздыванием.
С учетом этого запаздывания, величина рН на выходе из аппарата связана с расходом аммиака и кислоты (F,кг/с)
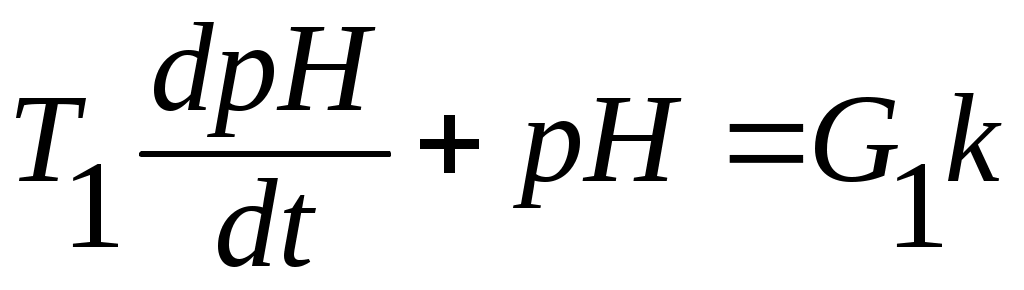
Таким образом, передаточная функция будет иметь вид
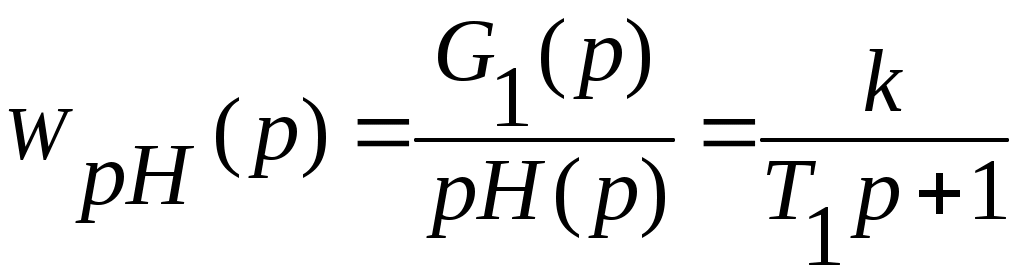 ,
,
где G1– суммарный расход реагентов;
k – коэффициент преобразования;
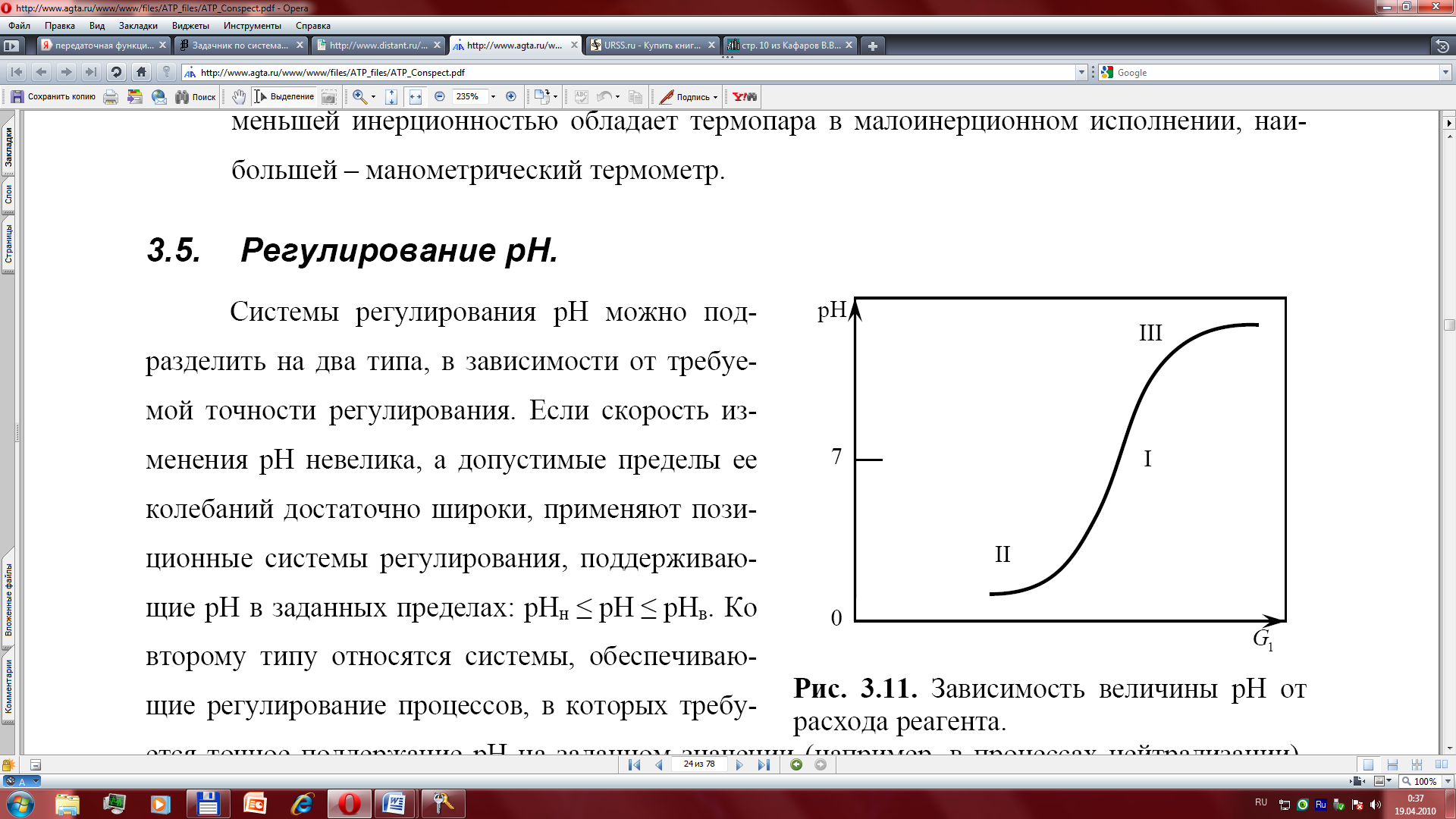
Рисунок 21 - Зависимость величины pH от суммарного расхода реагента
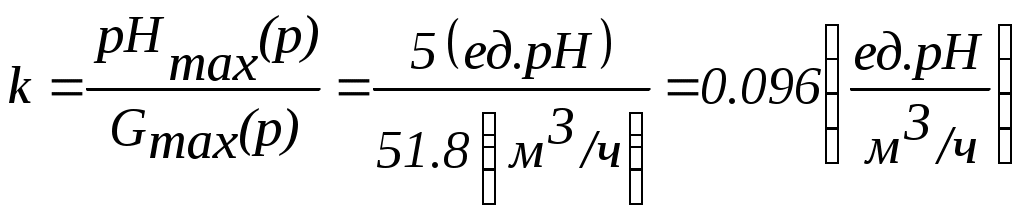
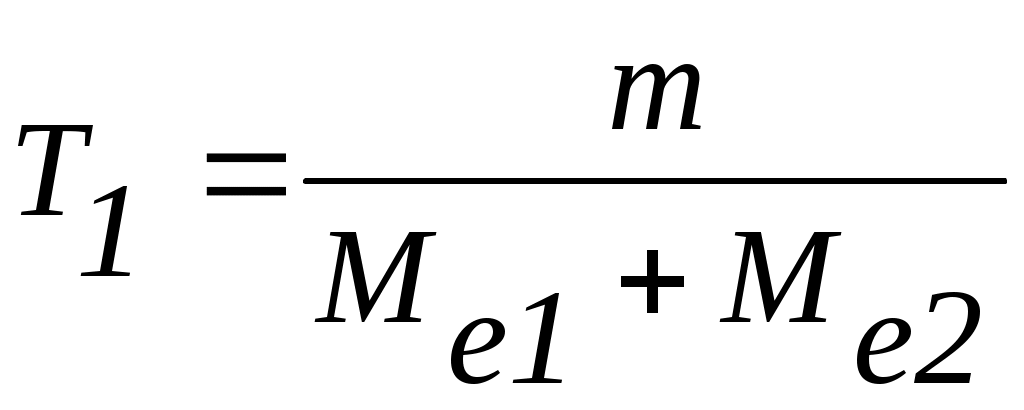 ,
,
где m – масса полученной пульпы, кг;
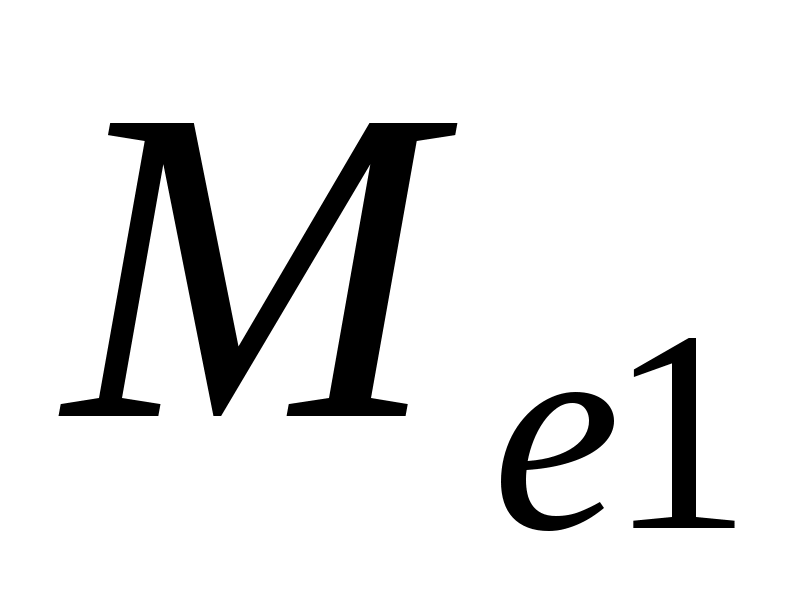 - расход кислоты, кг/ч;
- расход кислоты, кг/ч;
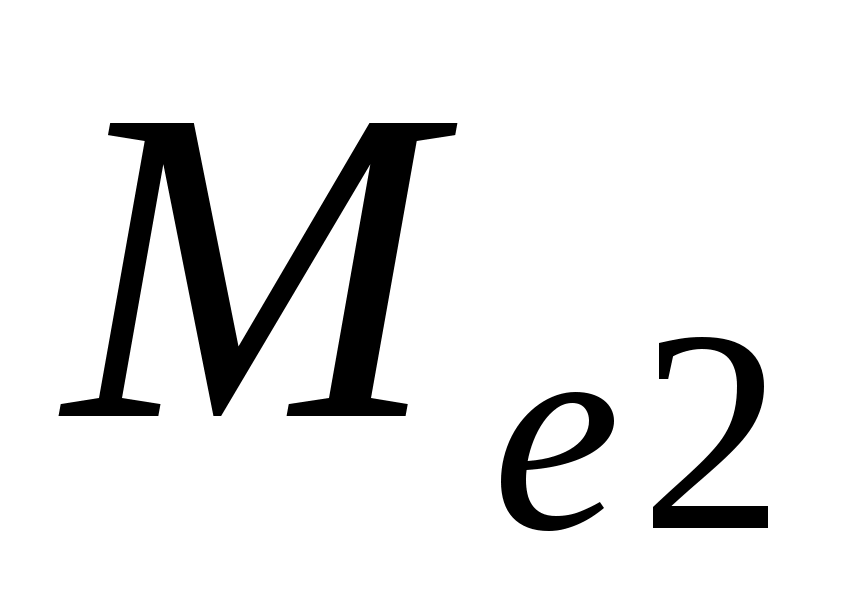
- расход аммиака, кг/ч.
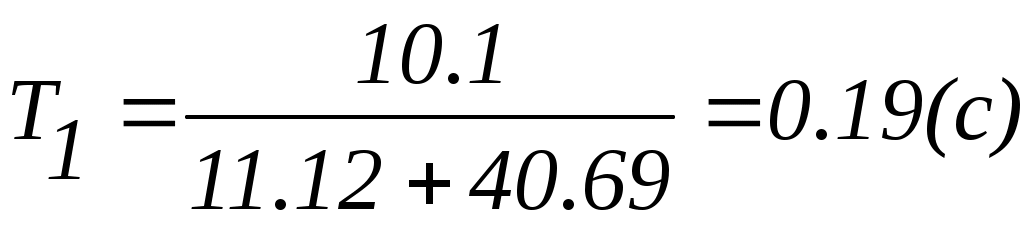
Подставив Т и k в передаточную функцию получим:
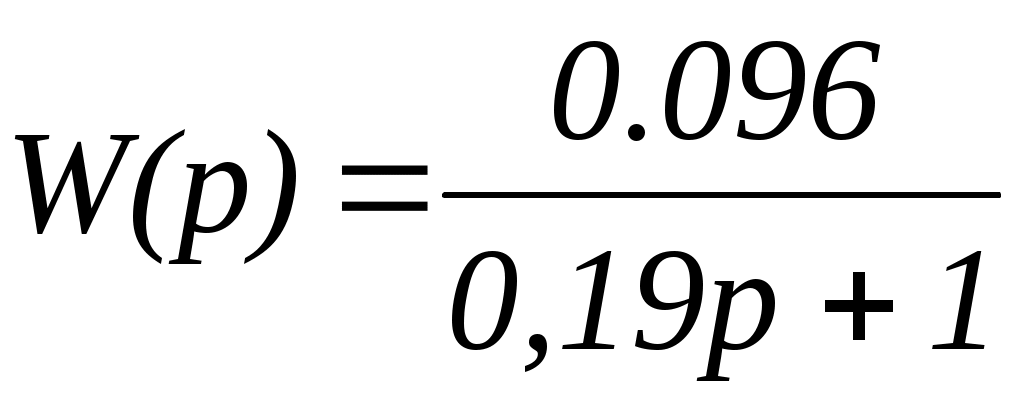 . (21)
. (21)
5 РАСЧЁТ УСТОЙЧИВОСТИ СИСТЕМЫ
5.1 Расчёт передаточной функции системы автоматического регулирования
Для расчетов передаточных функций и построения характеристик системы воспользуемся программой MATLAB и MathCad.
Структурная схема на основе передаточных функций полученных ранее.

Рисунок 21 – Функциональная схема
Передаточная функция замкнутой и разомкнутой системы имеет вид
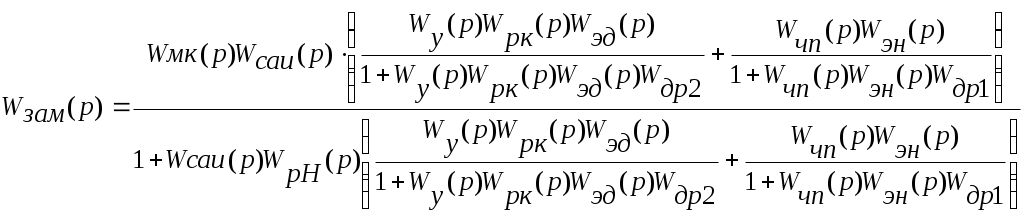
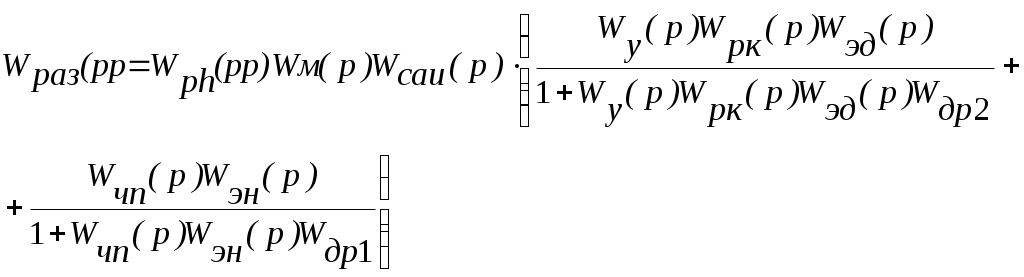
Определим передаточную функцию замкнутой и разомкнутой системы
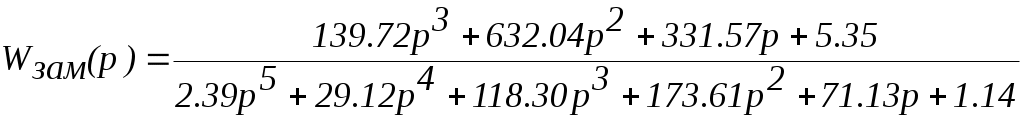
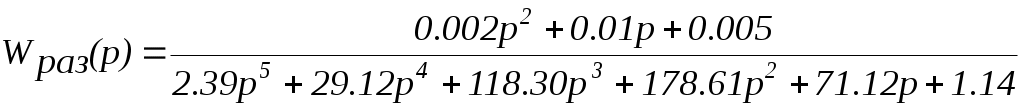
Так как в данной системе установлен цифровой микропроцессор, который осуществляет вычисление сигнала и посылает управляющие сигналы на устройства системы, то расчет следует провести для дискретной системы. При этом необходимо задать период дискретизации (интервал опроса датчиков) системы.
Чем меньше период дискретизации Т0, тем более дискретная система приближается по своим свойствам к непрерывной. Однако при слишком малых значениях Т0процессор в реальной системе может не успевать выполнять все необходимые вычисления. Кроме того, при уменьшении Т0 увеличивается число шагов переходного процесса. В силу сказанного, Т0 не должно быть слишком мало. Выберем период дискретизации равный постоянной времени ph-метра и деленным на 10. Т/10=6 с (опрос датчиков происходит примерно 6 раз в минуту).
5.2 Проверка устойчивости дискретной системы по частотному критерию
Частотный критерий устойчивости импульсных систем аналогичен критерию устойчивости Найквиста для непрерывных систем, и формулируется следующим образом: если разомкнутая импульсная система устойчива, то замкнутая импульсная система регулирования устойчива, если амплитудно-фазовая частотная характеристика (АФЧХ) разомкнутой системы не охватывает точку (-1; j0).
Проверим предварительно на устойчивость по критерию Ляпунова разомкнутую систему вида
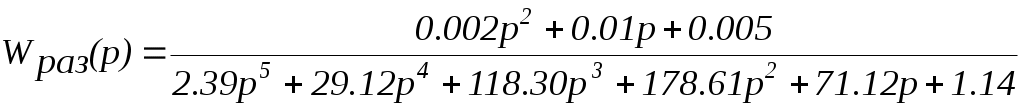
Для этого найдем корни характеристического уравнения.
p1=-3,92; p2=-0,59.
Поскольку все корни отрицательны и являются «левыми», то разомкнутая система устойчива.
Оценим устойчивость системы по критерию Найквиста.
Заменим в передаточной функции разомкнутой системы р на jω.
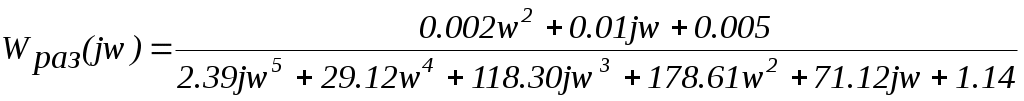
Построим АФЧХ разомкнутой системы предварительно выделив мнимую и действительную части.

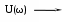
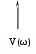
Рисунок 22 - АФЧХ разомкнутой дискретной системы
Так как АФЧХ разомкнутой системы, построенная на рисунке, не охватывает точку (-1; j0), то замкнутая импульсная система регулирования устойчива.
5.3 Построение логарифмических частотных характеристик системы и их анализ
Линейные типовые звенья можно разделить на два типа – непрерывные и дискретные. Частотные характеристики линейных непрерывных типовых звеньев находятся из передаточных функций после подстановки в них p = jω и выделения действительной и мнимой частей
W0 (jω) = U0 (ω) + jV0 (ω), (23)
где U0 (ω) и V0 (ω) – соответственно действительная и мнимая частотные характеристики.
Пользуясь выражением (23), в декартовой системе координат построим амплитудно-фазовые частотные характеристики W0 (jω). Если перейти к полярной системе координат, то выражение (23) можно переписать в виде
W0(jω) = H(ω) e jφ(ω), (24)
где H (ω) и φ(ω) – соответственно амплитудная и фазовая частотные характеристики.
Формулы для вычисления амплитудной и фазовой частотных характеристик:
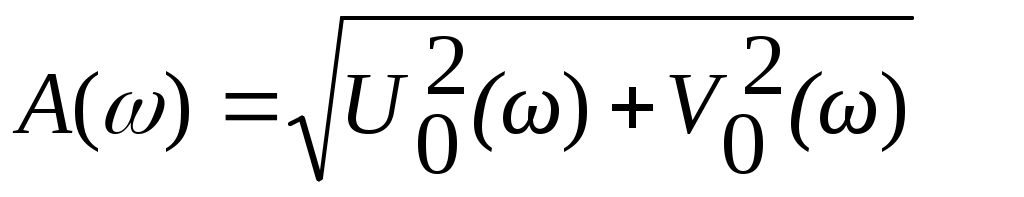 (25)
(25)
 (26)
(26)
Частотные характеристики линейных дискретных типовых звеньев находятся путем приведения к комплексной переменной jω которая связана с переменными
САПФИР-22ДД-2440 предназначен для преобразования в унифицированный токовый сигнал разности расхода газа (аммиака).
Основные технические характеристики САПФИР-22ДД-2440:
Верхние пределы измерения, МПА 0,63.
Пределы допускаемого рабочего избыточного давления, кгс/см2 10.
Выходные сигналы, мА от 0 до 5.
Пределы допускаемой основной погрешности, % 0,5.
Входной сигнал датчика расхода газа - расход Q:
- изменяется в переделах ∆Q, м3/ч 0 ÷ 19.
Выходной сигнал – ток:
- изменяется в приделах, мА 0 ÷ 5.
Вывод передаточной функции:
Зависимость между выходным и измеряемым параметром определяется выражением:
где
Зависимость между расходом Q и перепадом давления ΔP на диафрагме описывается выражением:
где d – диаметр диафрагмы, м;
ρ – плотность рабочей среды (для аммиака ρ=7710), кг/м3.
Для диафрагмы диафрагмы камерной ДКС-6-200 условный проход составляет Ду 200 мм, внутренний диаметр составляет d=0,05 м. Таким образом при измеряемом расходе Q=19м3/ч=40,69кг/с перепад давления рассчитывается следующим образом
Построим по данному выражению характеристику

I(Q)
Q
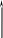

Рисунок 19– Характеристика преобразователя расхода в рабочем диапазоне
Или в системе СИ
Таким образом, передаточную функцию датчика расхода можно представить в виде усилительного звена с рассчитанным выше коэффициентом пропорциональности.
4.8 Выбор датчика рН пульпы и расчет передаточной функции
pH-метр — прибор для измерения концентрации ионов водорода (pH) в растворах и сырье, объектах окружающей среды и производственных систем непрерывного контроля технологических процессов.
Промышленный двухканальный рН-метр рН-4122 предназначен для автоматического измерения активности ионов водорода.

Рисунок 19 – Промышленный двухканальный рН-метр рН-4122
Прибор представляет собой двухканальное средство измерений и состоит из двух первичных преобразователей (ПП) рН-41211 и двухканального измерительного прибора (ИП).рН-4122 обеспечивает цифровую индикацию значений рН, преобразование их в пропорциональные значения унифицированных выходных сигналов постоянного тока, обмен данными по цифровому интерфейсу RS485, сигнализацию о выходе измеряемых параметров за пределы заданных значений.
Технические характеристики рН-метра рН-4122:
Время запаздывания, сек 60.
Количество измерительных каналов 2.
Диапазон измерений рН, ед. pH от 0 до 14.
Диапазон измерений ЭДС, мВ от минус 750 до плюс 750.
Температура анализируемой среды, ºС от 0 до плюс 100.
Предел допускаемого значения основной абсолютной погрешности:
- при измерении рН в комплекте с ЗС плюс минус 0,05.
- при измерении температуры плюс минус 0,5.
Тип индикатора жидкокристаллический графический.
Параметры сетевого питания, В, Гц 50.
Потребляемая мощность, Вт не более 15.
Входной сигнал рН-метра - ед. рН:
- изменяется в переделах, ед.рН 4 ÷ 5.
Выходной сигнал – ток:
- изменяется в приделах, мА 0 ÷ 5.
Передаточная функция:
где T – постоянная времени;
k – коэффициент преобразования.
4.9 Выбор скоростного аммонизатора-испарителя и расчет передаточной функции
САИ представляет собой «участок смешения» и «перемешивания» представленный на рисунке.


Me1- расход первого потока; Me2 – расход второго потока; Ma – поток полученный результате смешения
Рисунок 20 - Параметрическая схема двухкомпонентной системы
Технические характеристики САИ:
pH пульпы 4 ÷ 5.
Расход аммиака, кг/с 40,96.
Расход кислоты в САИ, кг/с 11,2.
Масса пульпы, кг, 10,1.
Диаметр САИ, мм 4020.
Высота, мм 9700.
Диаметр контура, мм 920.
Диаметр корпуса Dр , мм 200.
Диаметр патрубка ввода кислоты dк, мм 100.
Диаметр патрубка ввода аммиака dам, мм 125.
Диаметр сопла аммиака dсам, мм 100.
Диаметр сопла пульпы (на конце транспортной трубы) dп, мм 125.
Работа аммонизатора-испарителя основана на циркуляции потока кислоты и взаимодействии его с газообразным аммиаком и достаточно точно описываются дифференциальными уравнениями 1-го порядка с запаздыванием.
С учетом этого запаздывания, величина рН на выходе из аппарата связана с расходом аммиака и кислоты (F,кг/с)
Таким образом, передаточная функция будет иметь вид
где G1– суммарный расход реагентов;
k – коэффициент преобразования;

Рисунок 21 - Зависимость величины pH от суммарного расхода реагента
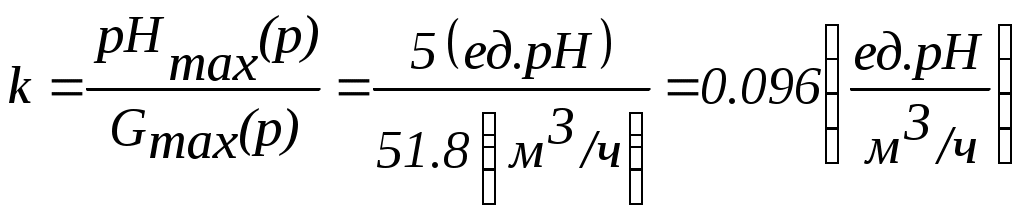
где m – масса полученной пульпы, кг;
- расход аммиака, кг/ч.
Подставив Т и k в передаточную функцию получим:
5 РАСЧЁТ УСТОЙЧИВОСТИ СИСТЕМЫ
5.1 Расчёт передаточной функции системы автоматического регулирования
Для расчетов передаточных функций и построения характеристик системы воспользуемся программой MATLAB и MathCad.
Структурная схема на основе передаточных функций полученных ранее.

Рисунок 21 – Функциональная схема
Передаточная функция замкнутой и разомкнутой системы имеет вид
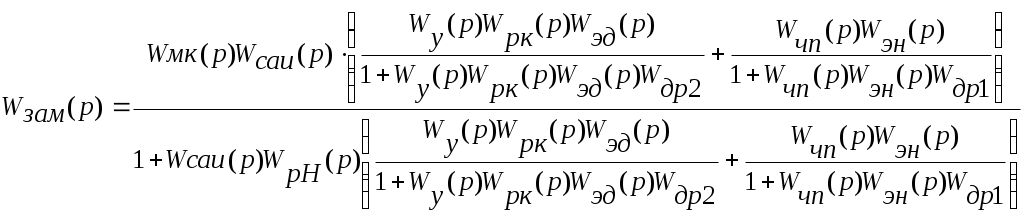
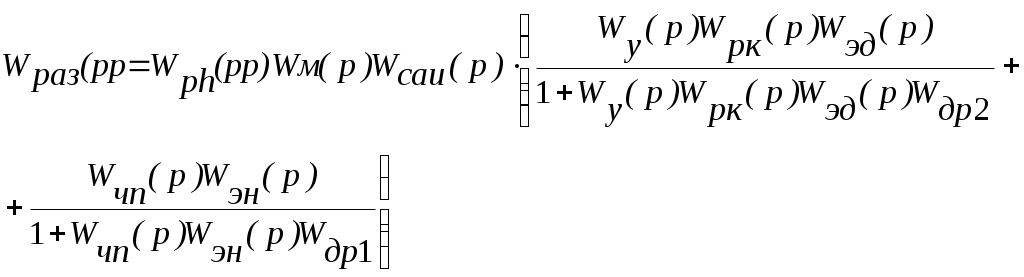
Определим передаточную функцию замкнутой и разомкнутой системы
Так как в данной системе установлен цифровой микропроцессор, который осуществляет вычисление сигнала и посылает управляющие сигналы на устройства системы, то расчет следует провести для дискретной системы. При этом необходимо задать период дискретизации (интервал опроса датчиков) системы.
Чем меньше период дискретизации Т0, тем более дискретная система приближается по своим свойствам к непрерывной. Однако при слишком малых значениях Т0процессор в реальной системе может не успевать выполнять все необходимые вычисления. Кроме того, при уменьшении Т0 увеличивается число шагов переходного процесса. В силу сказанного, Т0 не должно быть слишком мало. Выберем период дискретизации равный постоянной времени ph-метра и деленным на 10. Т/10=6 с (опрос датчиков происходит примерно 6 раз в минуту).
5.2 Проверка устойчивости дискретной системы по частотному критерию
Частотный критерий устойчивости импульсных систем аналогичен критерию устойчивости Найквиста для непрерывных систем, и формулируется следующим образом: если разомкнутая импульсная система устойчива, то замкнутая импульсная система регулирования устойчива, если амплитудно-фазовая частотная характеристика (АФЧХ) разомкнутой системы не охватывает точку (-1; j0).
Проверим предварительно на устойчивость по критерию Ляпунова разомкнутую систему вида
Для этого найдем корни характеристического уравнения.
p1=-3,92; p2=-0,59.
Поскольку все корни отрицательны и являются «левыми», то разомкнутая система устойчива.
Оценим устойчивость системы по критерию Найквиста.
Заменим в передаточной функции разомкнутой системы р на jω.
Построим АФЧХ разомкнутой системы предварительно выделив мнимую и действительную части.

Рисунок 22 - АФЧХ разомкнутой дискретной системы
Так как АФЧХ разомкнутой системы, построенная на рисунке, не охватывает точку (-1; j0), то замкнутая импульсная система регулирования устойчива.
5.3 Построение логарифмических частотных характеристик системы и их анализ
Линейные типовые звенья можно разделить на два типа – непрерывные и дискретные. Частотные характеристики линейных непрерывных типовых звеньев находятся из передаточных функций после подстановки в них p = jω и выделения действительной и мнимой частей
W0 (jω) = U0 (ω) + jV0 (ω), (23)
где U0 (ω) и V0 (ω) – соответственно действительная и мнимая частотные характеристики.
Пользуясь выражением (23), в декартовой системе координат построим амплитудно-фазовые частотные характеристики W0 (jω). Если перейти к полярной системе координат, то выражение (23) можно переписать в виде
W0(jω) = H(ω) e jφ(ω), (24)
где H (ω) и φ(ω) – соответственно амплитудная и фазовая частотные характеристики.
Формулы для вычисления амплитудной и фазовой частотных характеристик:
 (26)
(26)Частотные характеристики линейных дискретных типовых звеньев находятся путем приведения к комплексной переменной jω которая связана с переменными