Файл: Г. В. Савицкая Анализ хозяйственной деятельности предприятия.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 1259
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
R)
R =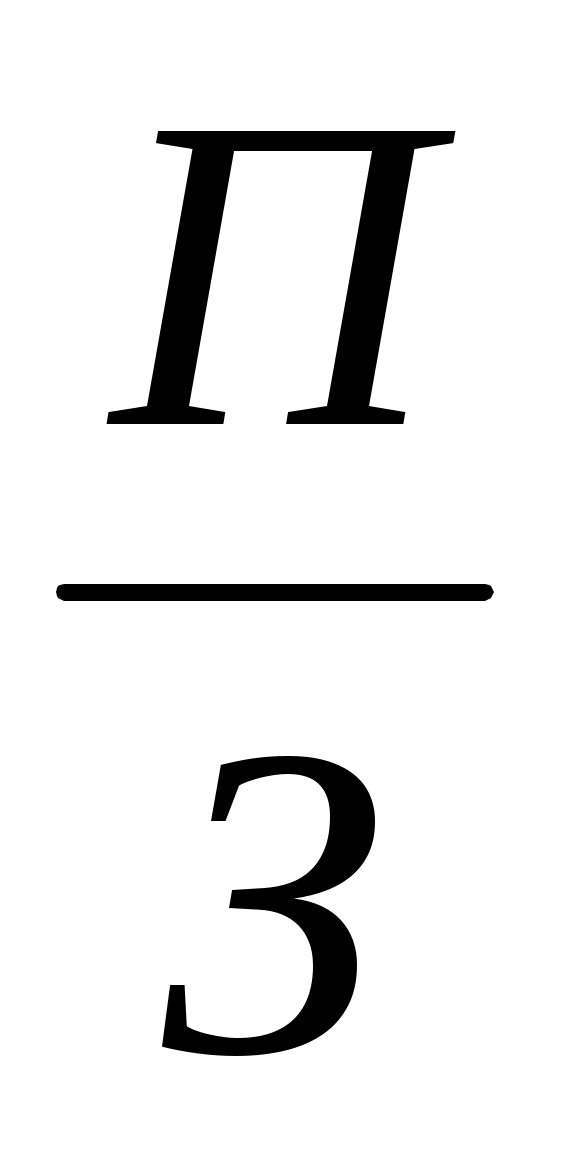
где П — сумма прибыли от реализации продукции;
З — сумма затрат на производство и реализацию продукции.
Если сумму затрат заменить на отдельные ее элементы, конечная модель в результате преобразования приобретет следующий вид:
R =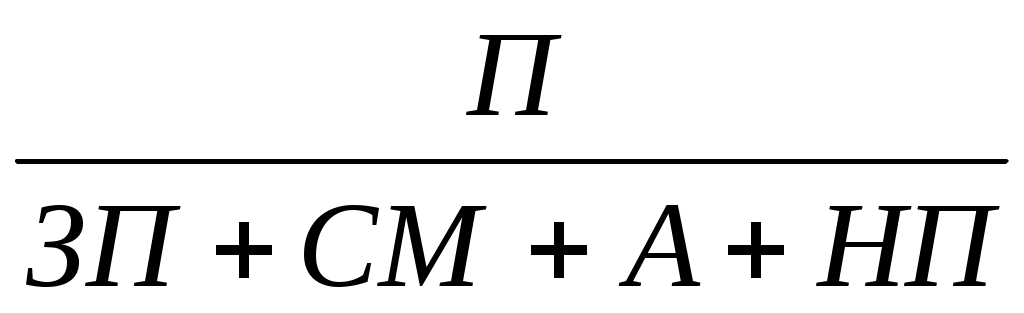
Себестоимость одного тонно-километра зависит от суммы затрат на содержание и эксплуатацию автомобиля (З) и от его среднегодовой выработки (ГВ). Исходная модель этой системы будет иметь вид: Сткм = З / ГВ. Учитывая, что среднегодовая выработка машины в свою очередь зависит от количества отработанных дней одним автомобилем за год (Д) продолжительности смены (Я) и среднечасовой выработки (ЧВ) мы можем значительно удлинить эту модель и разложить прирост себестоимости на большее количество факторов:
Сткм =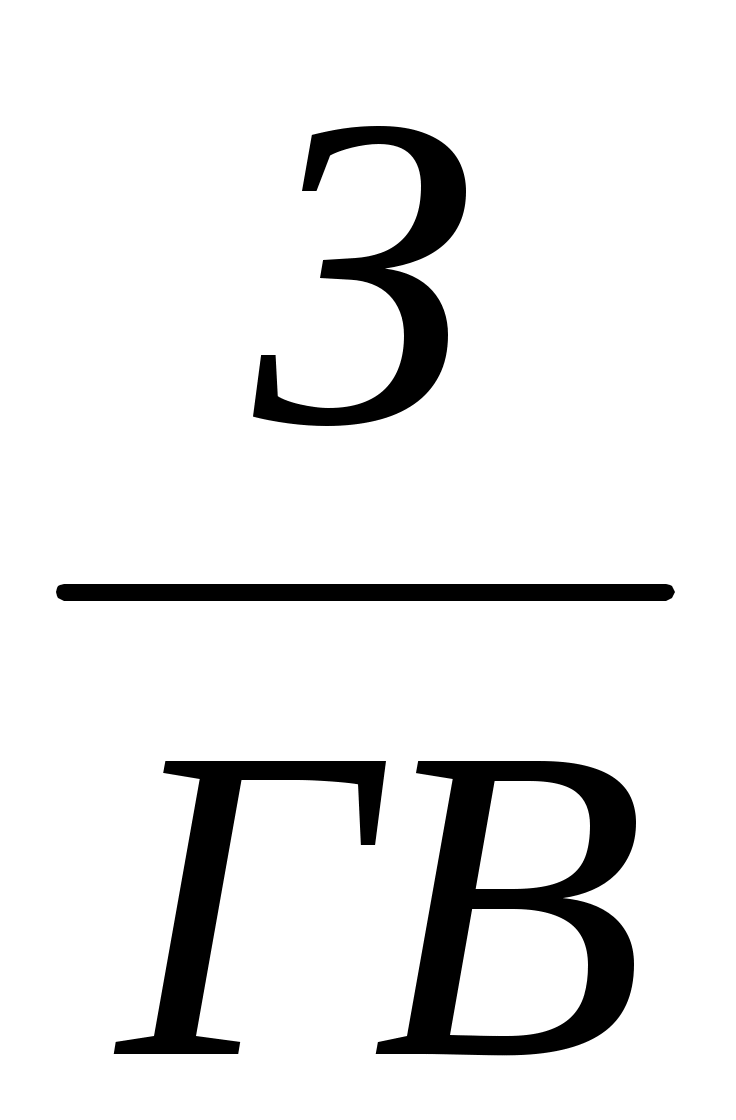
=
.
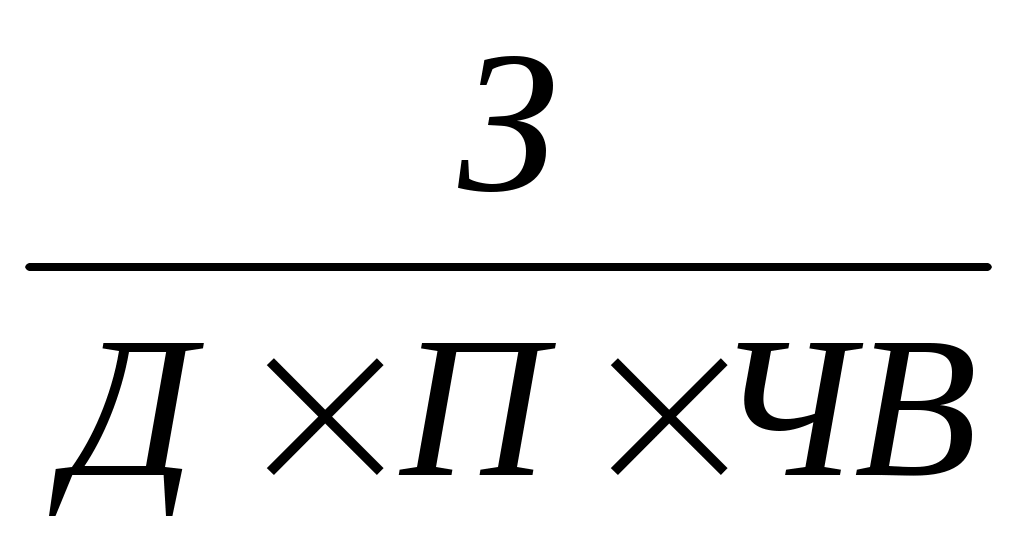Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель
Y = A / B
ввести новый показатель С, то модель примет вид
Y =
= 
= 
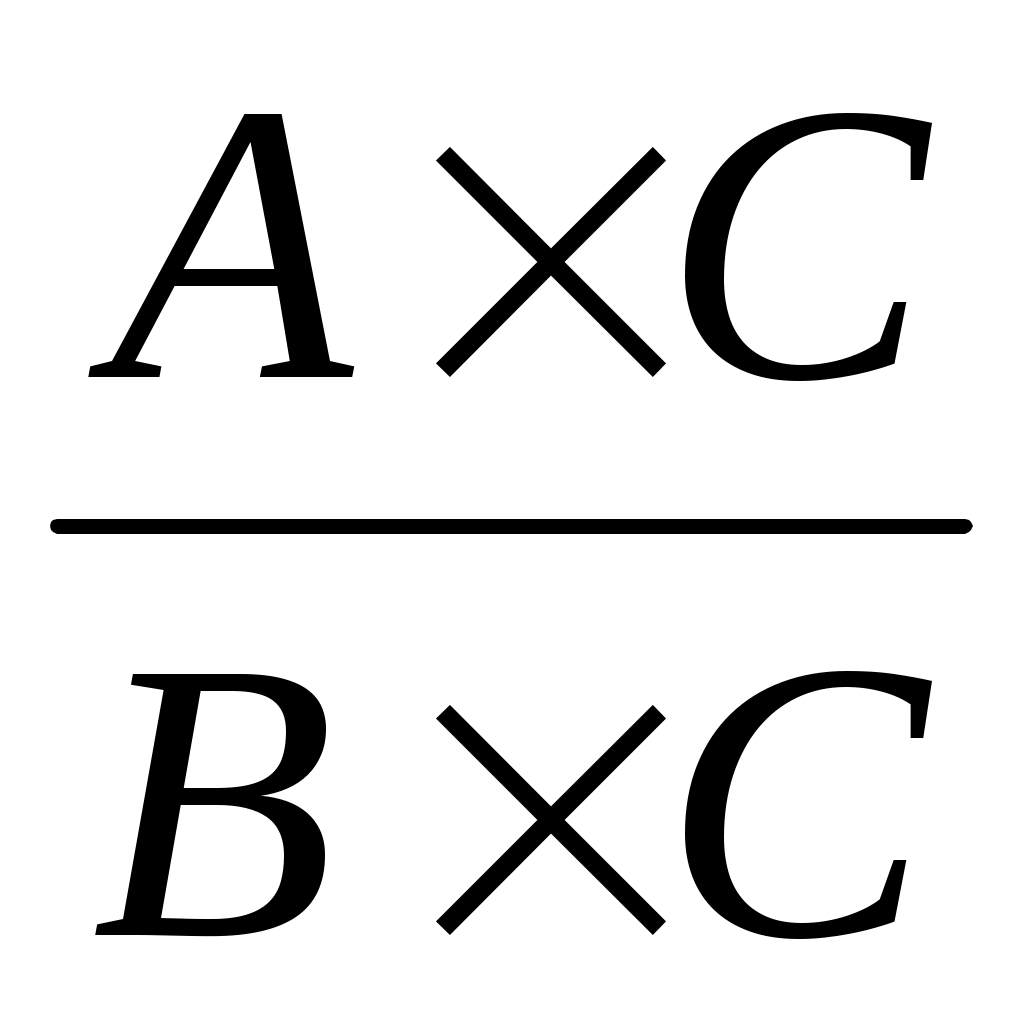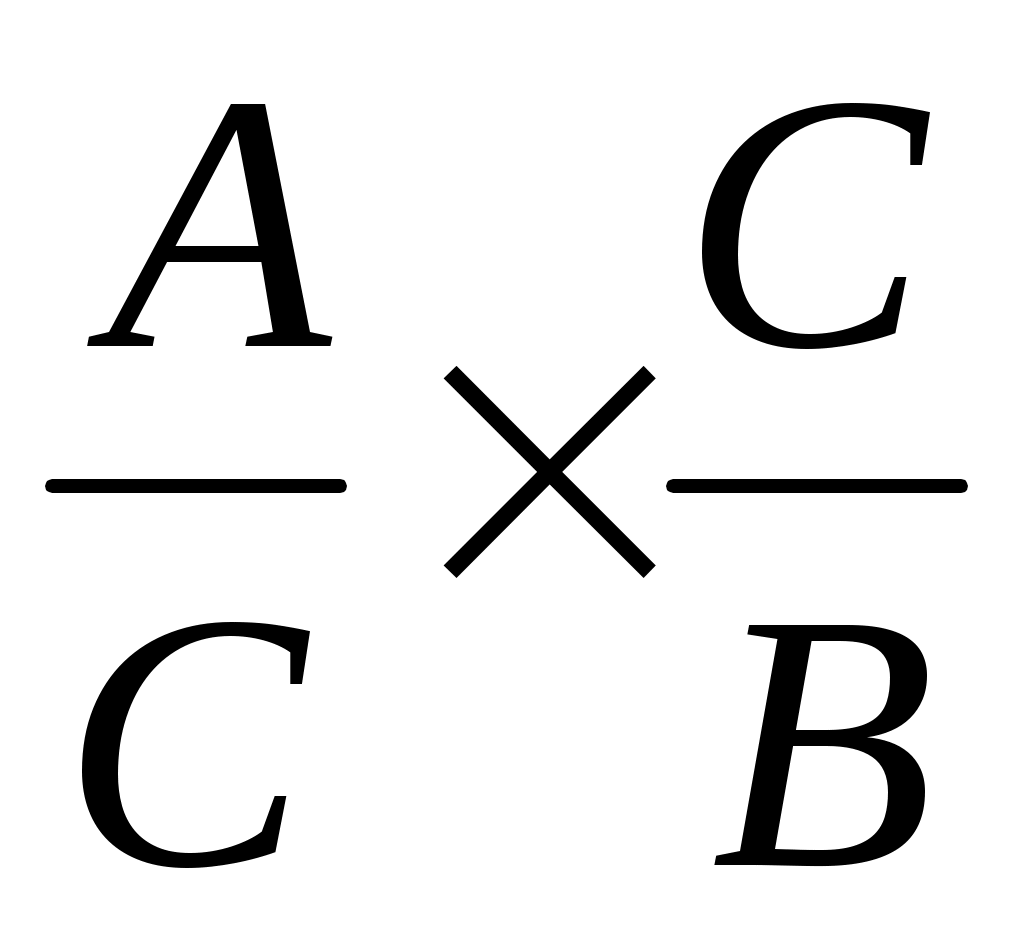= X1 × X2.
В результате получилась конечная мультипликативная модель в виде произведения нового набора факторов.
Этот способ моделирования очень широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ = ВП / ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками (D), то получим следующую модель годовой выработки:
ГВ =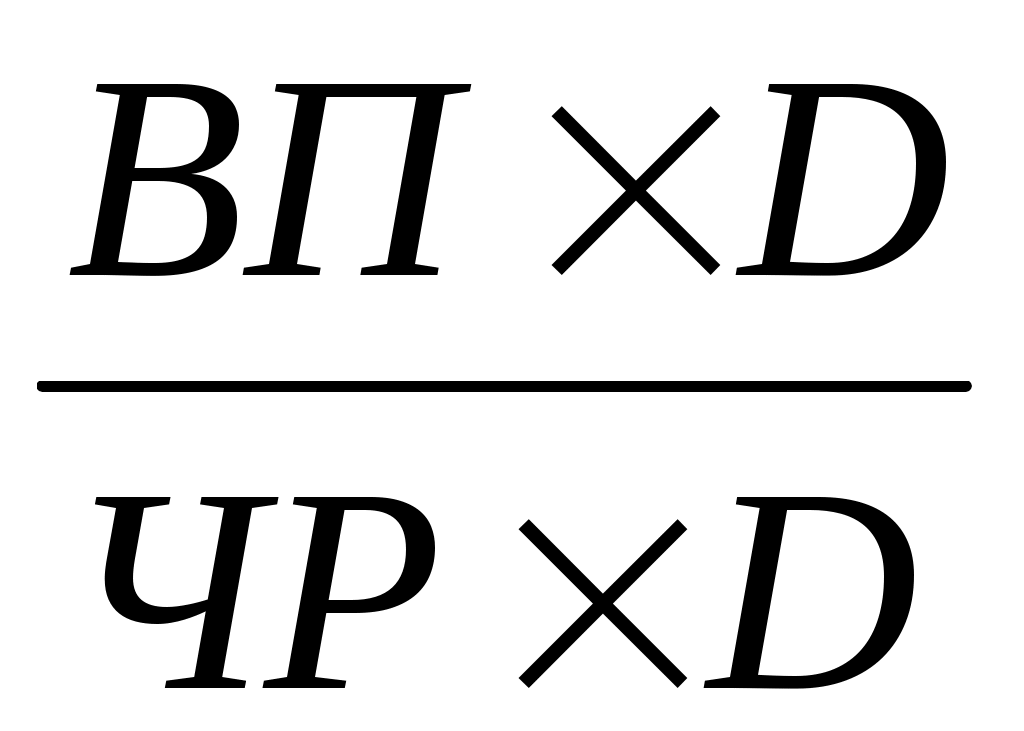
= 
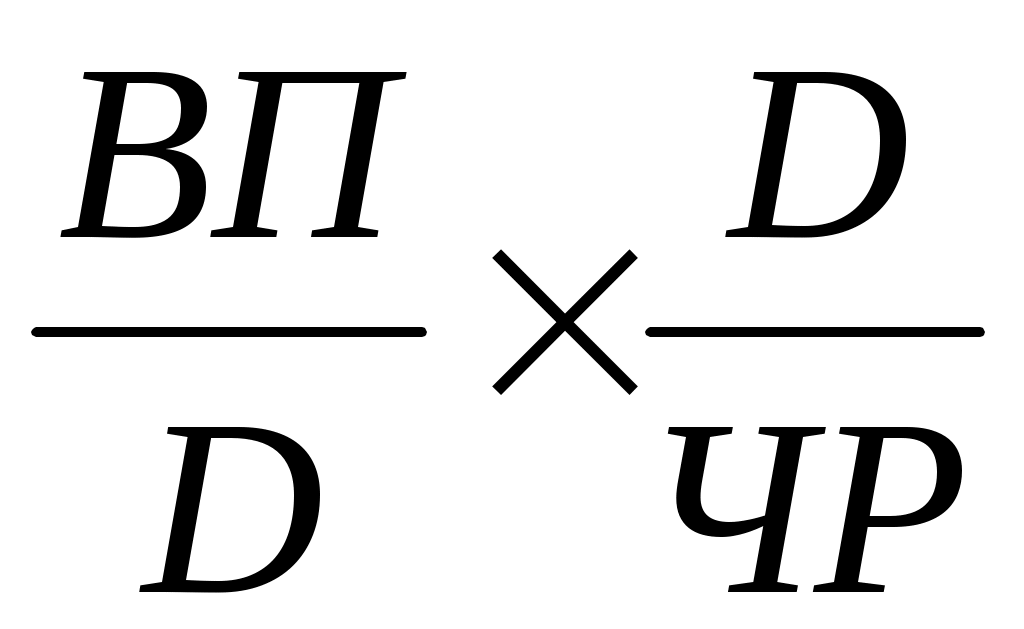= ДВ × Д,
где ДВ — среднедневная выработка;
Д — количество отработанных дней одним работником.
После введения показателя количества отработанных часов всеми работниками (Т) получим модель с новым набором факторов: среднечасовой выработки (ЧВ), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (П).
ГВ =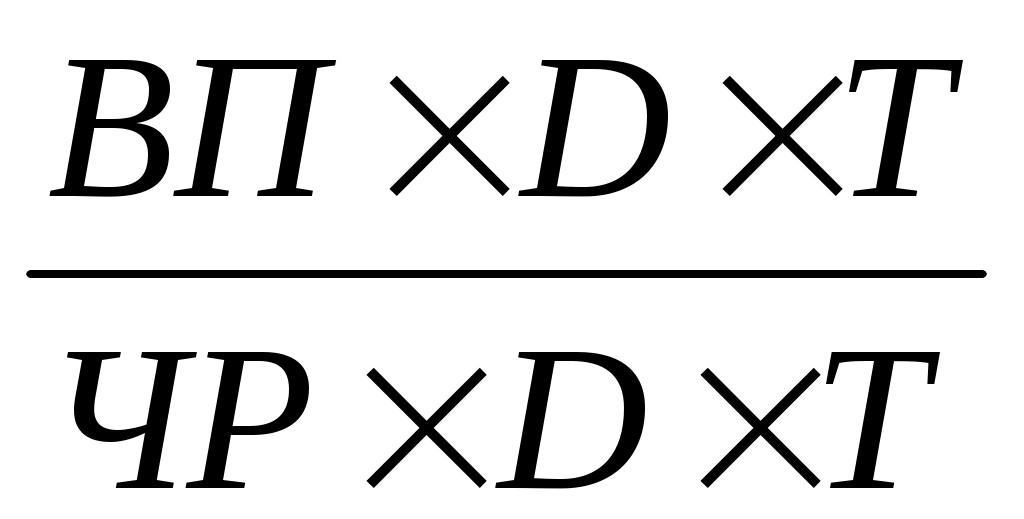
= 
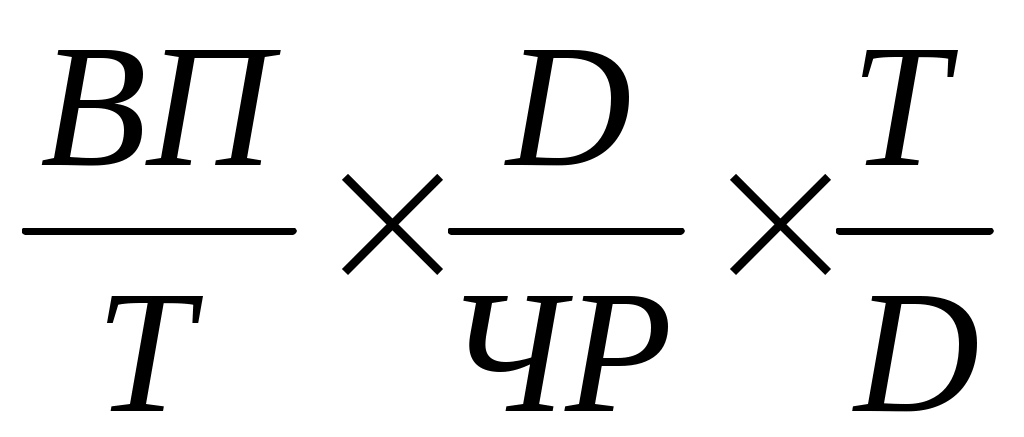= ЧВ × Д × П.
Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель:
Y = = 
=
.
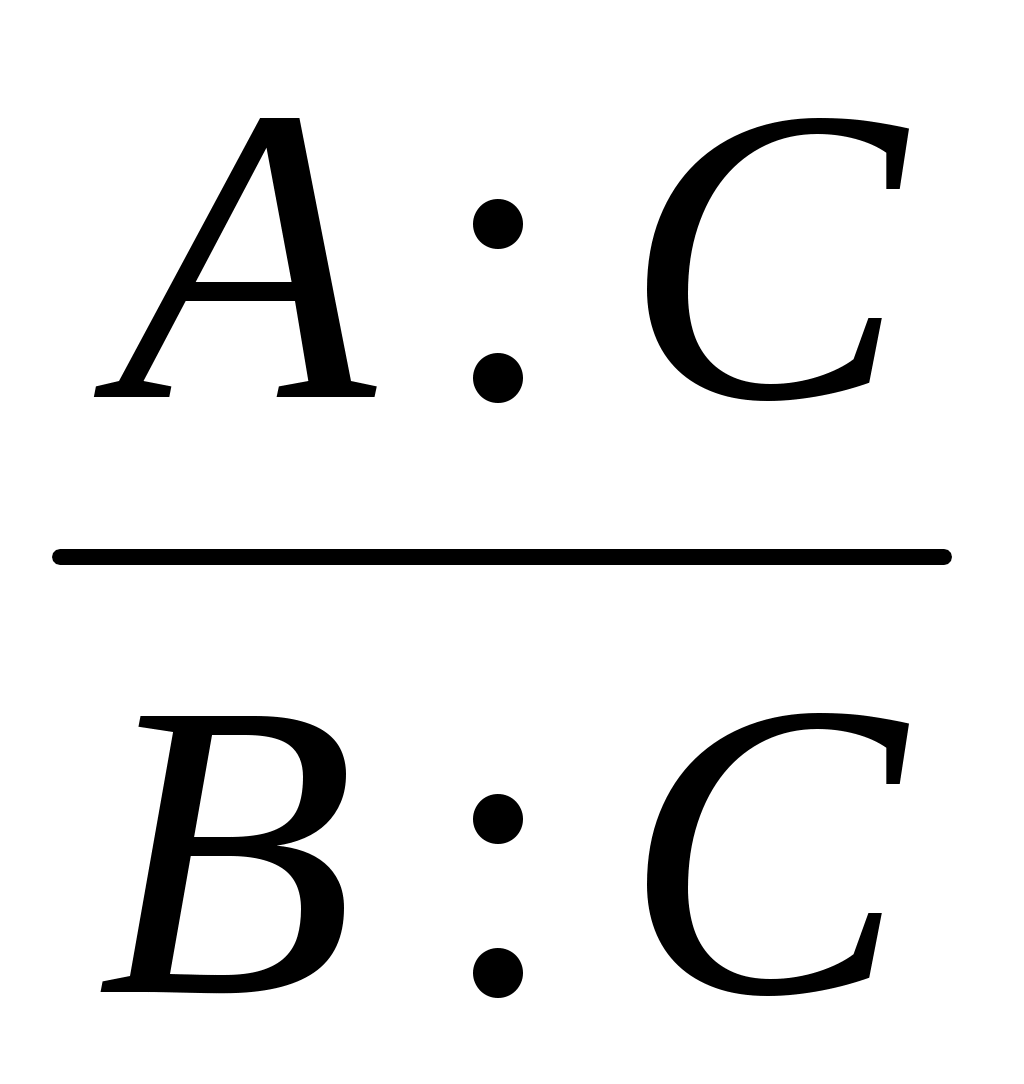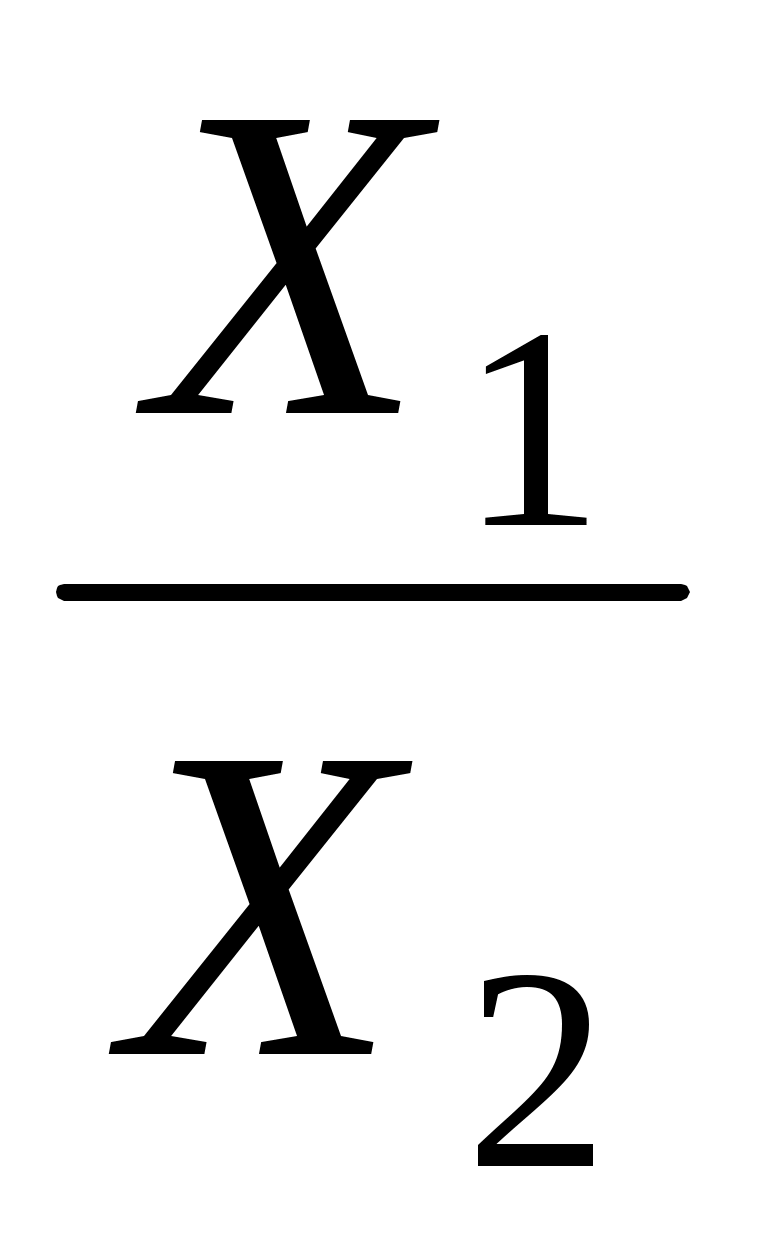В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.
И снова практический пример. Как известно, рентабельность операционного капитала рассчитывается делением суммы прибыли от реализации продукции (П) на среднегодовую стоимость основного и оборотного капитала предприятия (KL):
R = П / KL.
Если числитель и знаменатель разделим на объем реализации продукции (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:
R =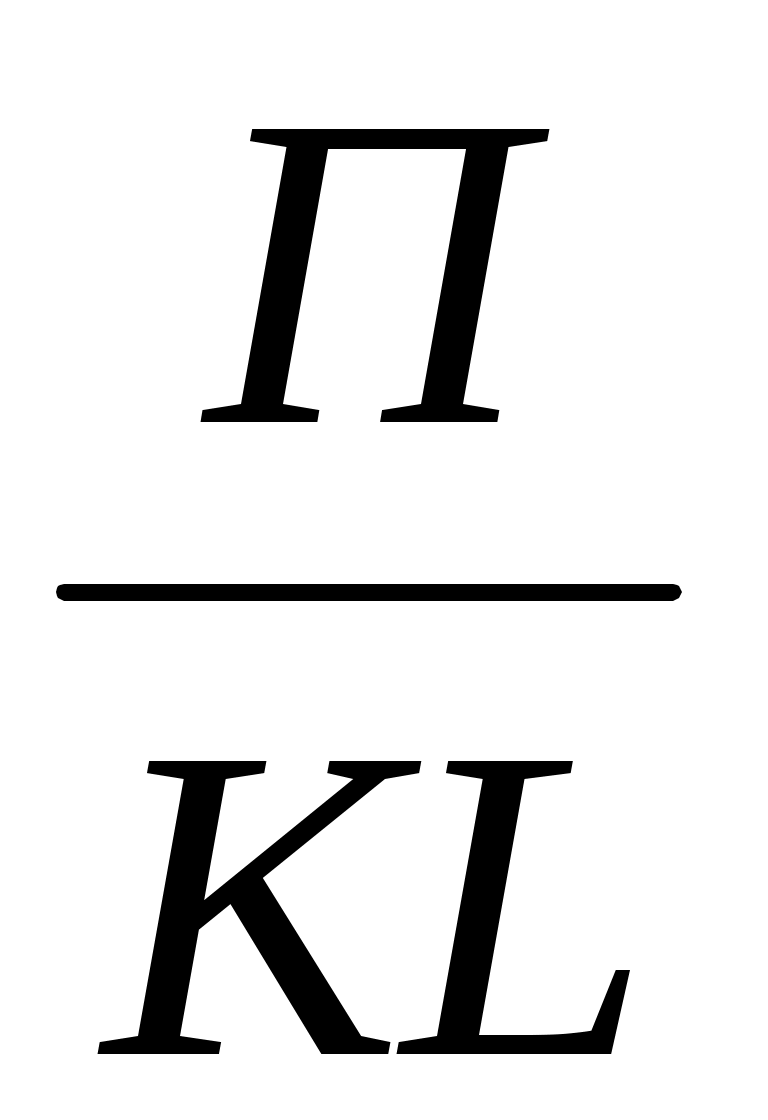
= 
= 
.
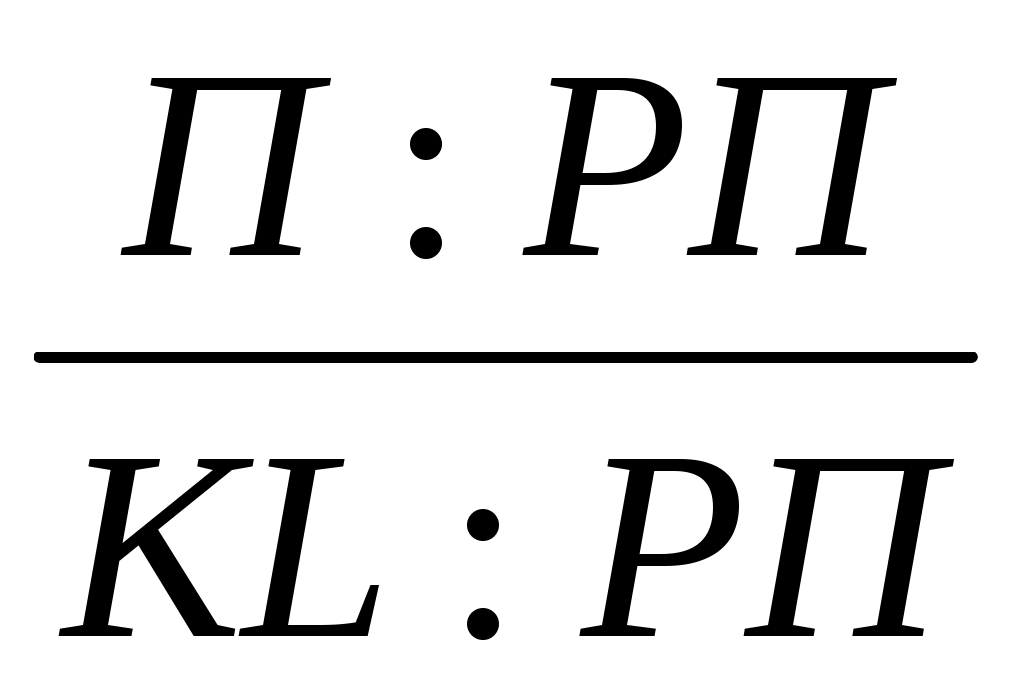И еще один пример. Фондоотдача (ФО)определяется отношением валовой (ВП)или товарной продукции (ТП) к среднегодовой стоимости основных производственных фондов (ОПФ):
ФО =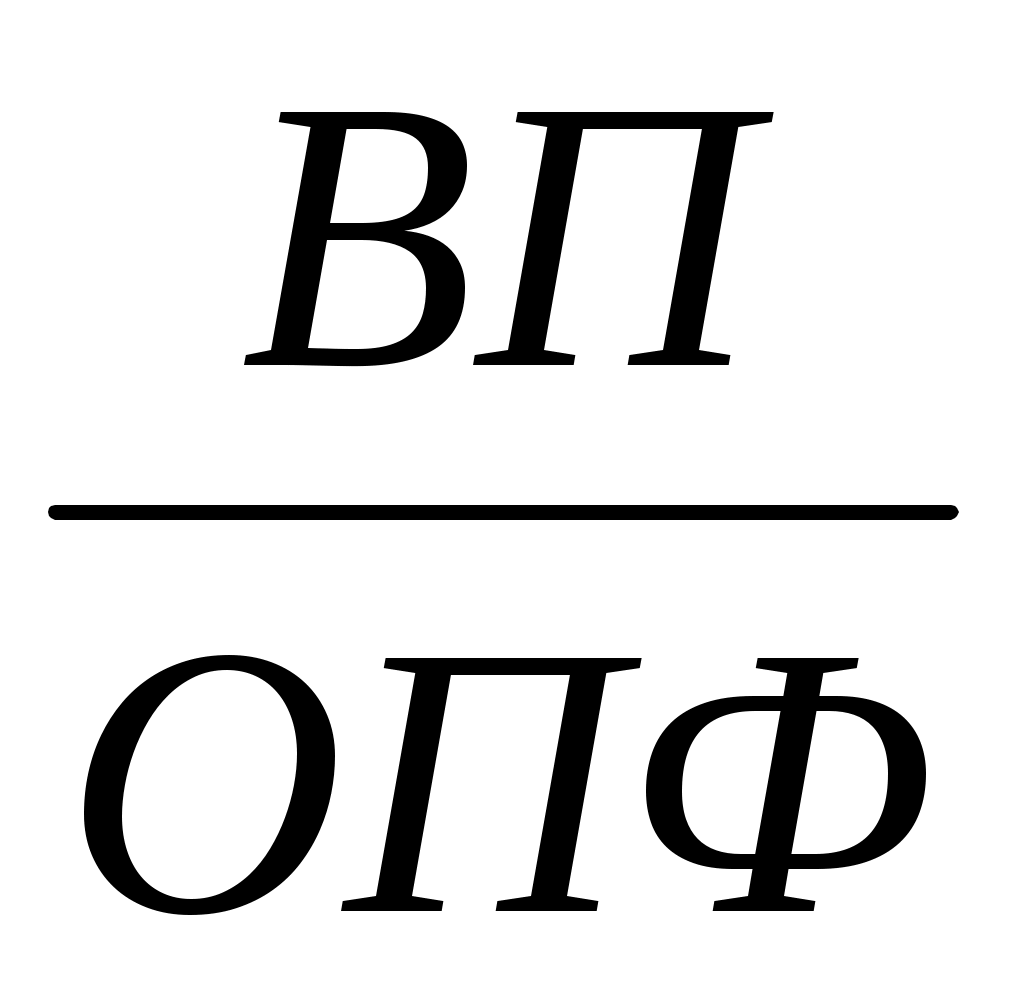
.
Разделив числитель и знаменатель на среднегодовое количество рабочих (ЧР), получим более содержательную кратную модель с другими факторными показателями: среднегодовой выработки продукции одним рабочим (ГВ), характеризующей уровень производительности труда, и фондовооруженности труда (Фв)
ФО =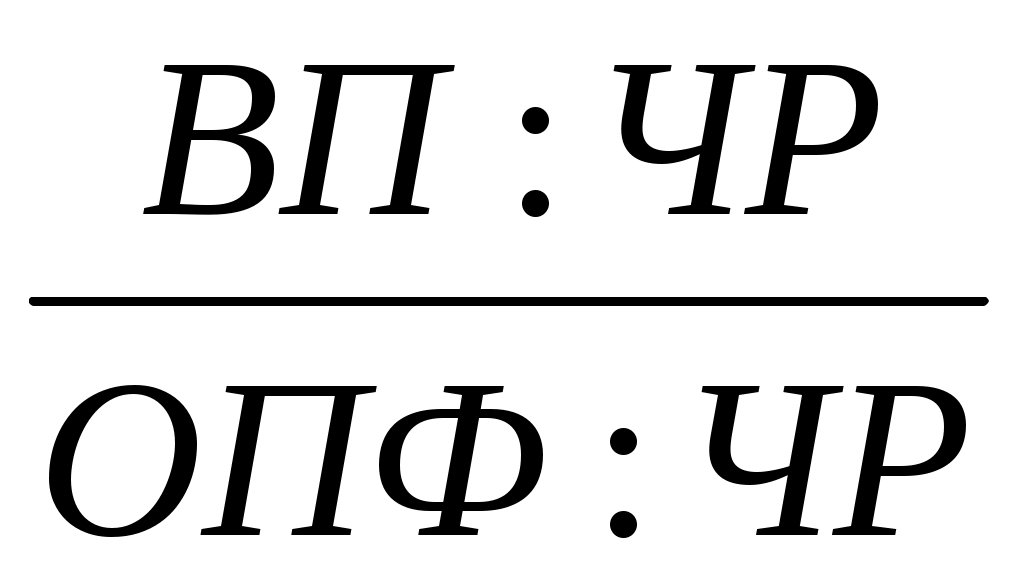
= 
.
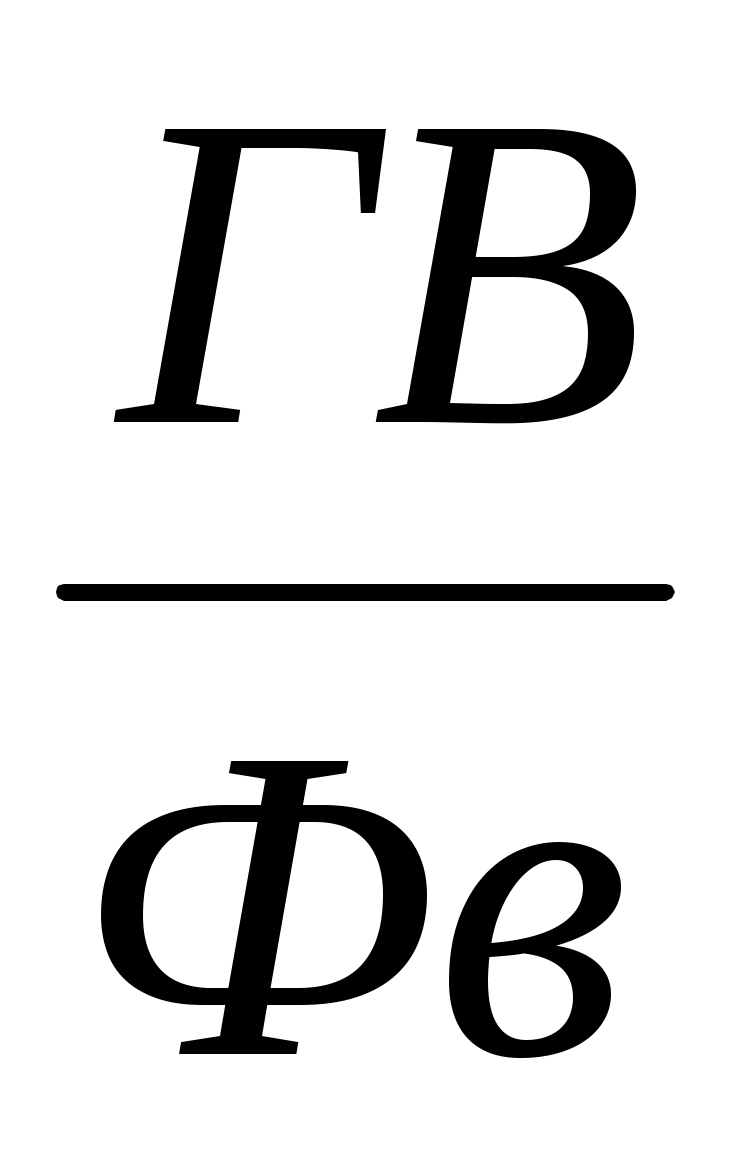
Необходимо заметить, что на практике для преобразования одной и той же модели может быть последовательно использовано несколько методов. Например, процесс создания факторной модели рентабельности совокупного капитала (RKL)можно представить следующим образом:
RKL =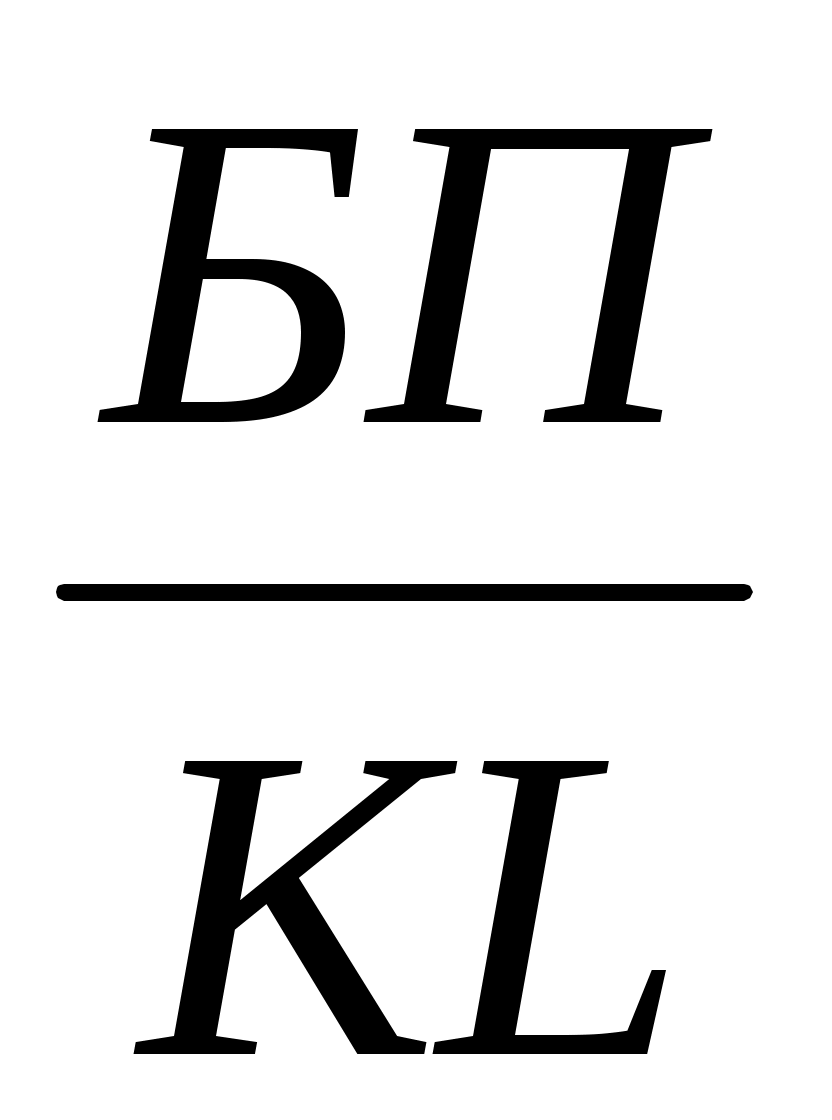
= 
= 
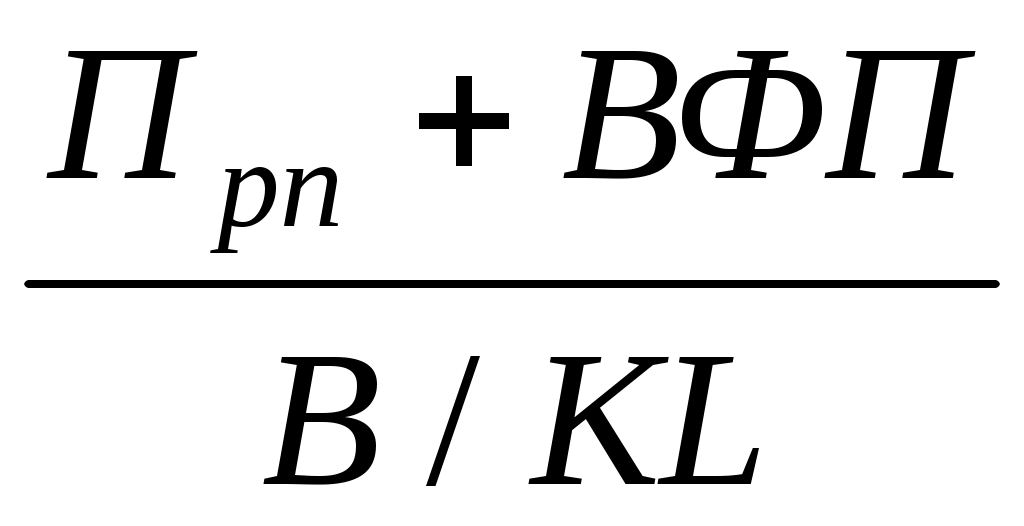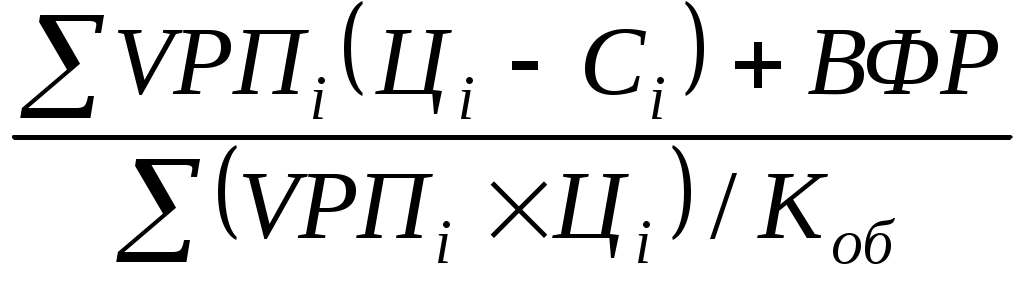
где БП — сумма балансовой (валовой) прибыли за отчетный период;
KL — среднегодовая сумма совокупного капитала;
Прп — прибыль от реализации продукции (услуг);
ВФР — внереализационные финансовые результаты;
В — выручка от реализации продукции (услуг);
VРПi — объем реализации продукции вида в натуральном выражении;
Цi— отпускные цены на i-йвид продукции;
Ci— себестоимость единицы i-го вида продукции;
Коб — коэффициент оборачиваемости совокупного капитала за отчетный период (отношение выручки к среднегодовой сумме капитала).
В данном случае для преобразования исходной факторной модели, построенной на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель мультипликативно-аддитивно-кратного вида, которая имеет большую познавательную ценность, поскольку учитывает причинно-следственные связи между показателями. Данная модель позволяет исследовать, как влияют на доходность капитала объем продаж, отпускные цены, себестоимость реализованной продукции, внереализационные финансовые результаты, а также скорость обращения капитала.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, от поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем — очень сложный и ответственный момент в АХД. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Глава 6. СПОСОБЫ ИЗМЕРЕНИЯ ВЛИЯНИЯ ФАКТОРОВ В ДЕТЕРМИНИРОВАННОМ АНАЛИЗЕ
6.1. Способ цепной подстановки
Типы детерминированных моделей, в которых применяется способ цепной подстановки. Сущность и правила его применения. Алгоритмы расчета влияния факторов этим способом в различных типах моделей.
Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном факторном анализе (ДФА) для этого используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.
Первые четыре способа основываются на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня определенного фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
Порядок применения этого способа рассмотрим на следующем примере (табл. 6.1).
Т а б л и ц а 6.1
Данные для факторного анализа объема валовой продукции
R =
где П — сумма прибыли от реализации продукции;
З — сумма затрат на производство и реализацию продукции.
Если сумму затрат заменить на отдельные ее элементы, конечная модель в результате преобразования приобретет следующий вид:
R =
Себестоимость одного тонно-километра зависит от суммы затрат на содержание и эксплуатацию автомобиля (З) и от его среднегодовой выработки (ГВ). Исходная модель этой системы будет иметь вид: Сткм = З / ГВ. Учитывая, что среднегодовая выработка машины в свою очередь зависит от количества отработанных дней одним автомобилем за год (Д) продолжительности смены (Я) и среднечасовой выработки (ЧВ) мы можем значительно удлинить эту модель и разложить прирост себестоимости на большее количество факторов:
Сткм =
= .Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель
Y = A / B
ввести новый показатель С, то модель примет вид
Y =
= = = X1 × X2.В результате получилась конечная мультипликативная модель в виде произведения нового набора факторов.
Этот способ моделирования очень широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ = ВП / ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками (D), то получим следующую модель годовой выработки:
ГВ =
= = ДВ × Д,где ДВ — среднедневная выработка;
Д — количество отработанных дней одним работником.
После введения показателя количества отработанных часов всеми работниками (Т) получим модель с новым набором факторов: среднечасовой выработки (ЧВ), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (П).
ГВ =
= = ЧВ × Д × П.Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель:
Y =
= = .В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.
И снова практический пример. Как известно, рентабельность операционного капитала рассчитывается делением суммы прибыли от реализации продукции (П) на среднегодовую стоимость основного и оборотного капитала предприятия (KL):
R = П / KL.
Если числитель и знаменатель разделим на объем реализации продукции (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:
R =
= = .И еще один пример. Фондоотдача (ФО)определяется отношением валовой (ВП)или товарной продукции (ТП) к среднегодовой стоимости основных производственных фондов (ОПФ):
ФО =
.Разделив числитель и знаменатель на среднегодовое количество рабочих (ЧР), получим более содержательную кратную модель с другими факторными показателями: среднегодовой выработки продукции одним рабочим (ГВ), характеризующей уровень производительности труда, и фондовооруженности труда (Фв)
ФО =
=
.
Необходимо заметить, что на практике для преобразования одной и той же модели может быть последовательно использовано несколько методов. Например, процесс создания факторной модели рентабельности совокупного капитала (RKL)можно представить следующим образом:
RKL =
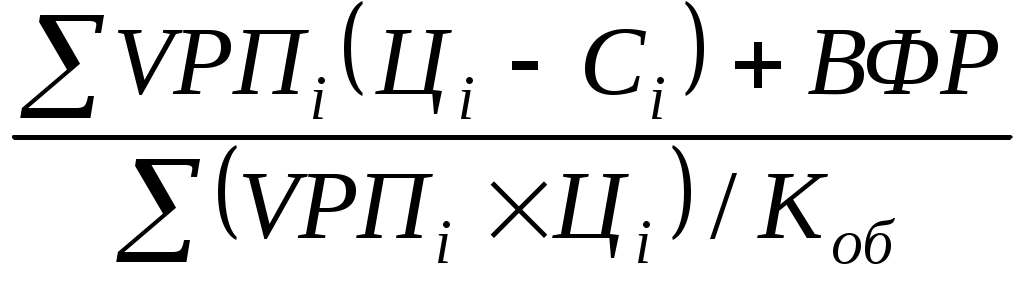
= = где БП — сумма балансовой (валовой) прибыли за отчетный период;
KL — среднегодовая сумма совокупного капитала;
Прп — прибыль от реализации продукции (услуг);
ВФР — внереализационные финансовые результаты;
В — выручка от реализации продукции (услуг);
VРПi — объем реализации продукции вида в натуральном выражении;
Цi— отпускные цены на i-йвид продукции;
Ci— себестоимость единицы i-го вида продукции;
Коб — коэффициент оборачиваемости совокупного капитала за отчетный период (отношение выручки к среднегодовой сумме капитала).
В данном случае для преобразования исходной факторной модели, построенной на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель мультипликативно-аддитивно-кратного вида, которая имеет большую познавательную ценность, поскольку учитывает причинно-следственные связи между показателями. Данная модель позволяет исследовать, как влияют на доходность капитала объем продаж, отпускные цены, себестоимость реализованной продукции, внереализационные финансовые результаты, а также скорость обращения капитала.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, от поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем — очень сложный и ответственный момент в АХД. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Глава 6. СПОСОБЫ ИЗМЕРЕНИЯ ВЛИЯНИЯ ФАКТОРОВ В ДЕТЕРМИНИРОВАННОМ АНАЛИЗЕ
6.1. Способ цепной подстановки
Типы детерминированных моделей, в которых применяется способ цепной подстановки. Сущность и правила его применения. Алгоритмы расчета влияния факторов этим способом в различных типах моделей.
Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном факторном анализе (ДФА) для этого используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.
Первые четыре способа основываются на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня определенного фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
Порядок применения этого способа рассмотрим на следующем примере (табл. 6.1).
Т а б л и ц а 6.1
Данные для факторного анализа объема валовой продукции
| Показатель | Условное обозначение | План | Факт | + ,- | Выполнение плана, % |
| Выпуск продукции, тыс. руб. | ВП | 160 000 | 240 000 | +80 000 | 150 |
| Среднегодовая численность рабочих, чел. | ЧР | 1000 | 1200 | +200 | 120 |
| Отработано всеми рабочими за год: | | | | | |
| дней | D | 250 000 | 307 200 | +57 200 | 122,88 |
| часов | t | 2 000 000 | 2 334 720 | +334 720 | 116,736 |
| Среднегодовая выработка одного рабочего, тыс. руб. | ГВ | 160 | 200 | +40 | 125 |
| Количество отработанных дней одним рабочим за год | Д | 250 | 256 | +6 | 102,4 |
| Среднедневная выработка продукции одним рабочим, руб. | ДВ | 640 | -781,25 | + 141,25 | 122,1 |
| Средняя продолжительность рабочего дня, ч. | П | 8 | 7.6 | -0.4 | 95 |
| Среднечасовая выработка, руб. | ЧВ | 80 | 102,796 | +22,796 | 128,5 |