Добавлен: 23.11.2023
Просмотров: 322
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
По величине упругая сила Fупр равна внешней силе F, приложенной вдоль верхнего основания цилиндра, площадь которого S. Поэтому напряжение сдвига (касательное напряжение):
По закону Гука (справедливому при малых напряжениях) относительный сдвиг φ пропорционален касательному напряжению:
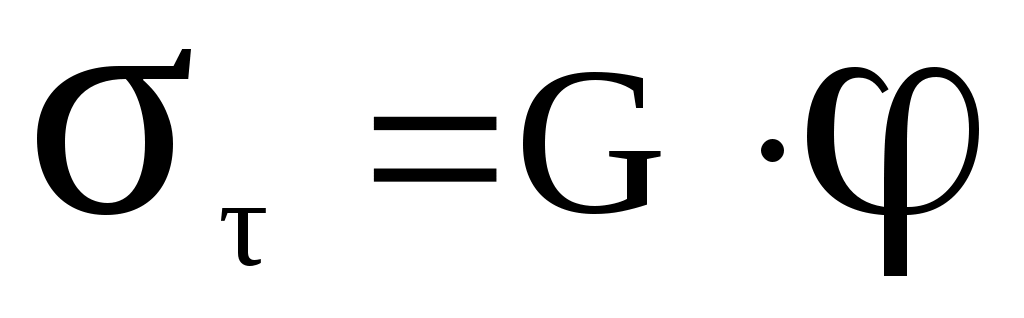 , (3)
, (3)где модуль сдвига для чугуна равен
Поскольку размеры чугунного и свинцового цилиндров, и силы, приложенные к ним, одинаковы то из (2) следует равенство касательных напряжений для этих цилиндров, поэтому, используя (3):

Для абсолютного сдвига из (1) получаем соотношение:
Таким образом, как относительный сдвиг φ так и абсолютный сдвиг
Задача 3*
Плоская продольная упругая волна распространяется в положительном направлении оси x в среде с плотностью
.
Анализ и решение
Колебание смещений частиц в плоской произвольной упругой волне, распространяющейся в положительном направлении оси x, можно записать:
где ω – частота звука, k – волновое число, а
Скорость смещения частиц в среде вдоль оси xнайдется дифференцированием функции S(x,t) по времени:
Относительная деформация среды будет:
Связь между
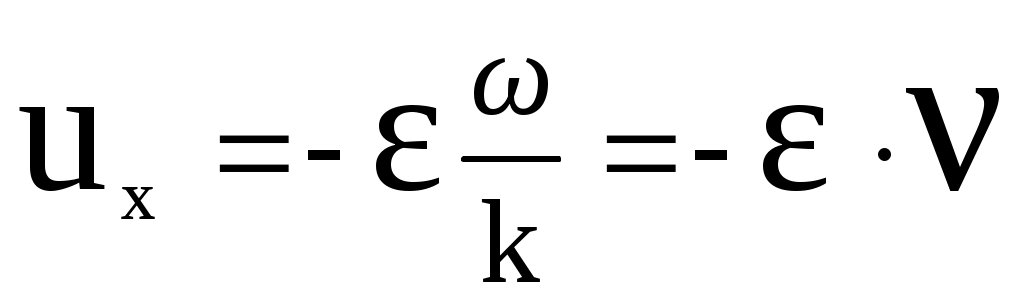 .
.Т.к. фазовая скорость произвольных волн в упругой среде равна:
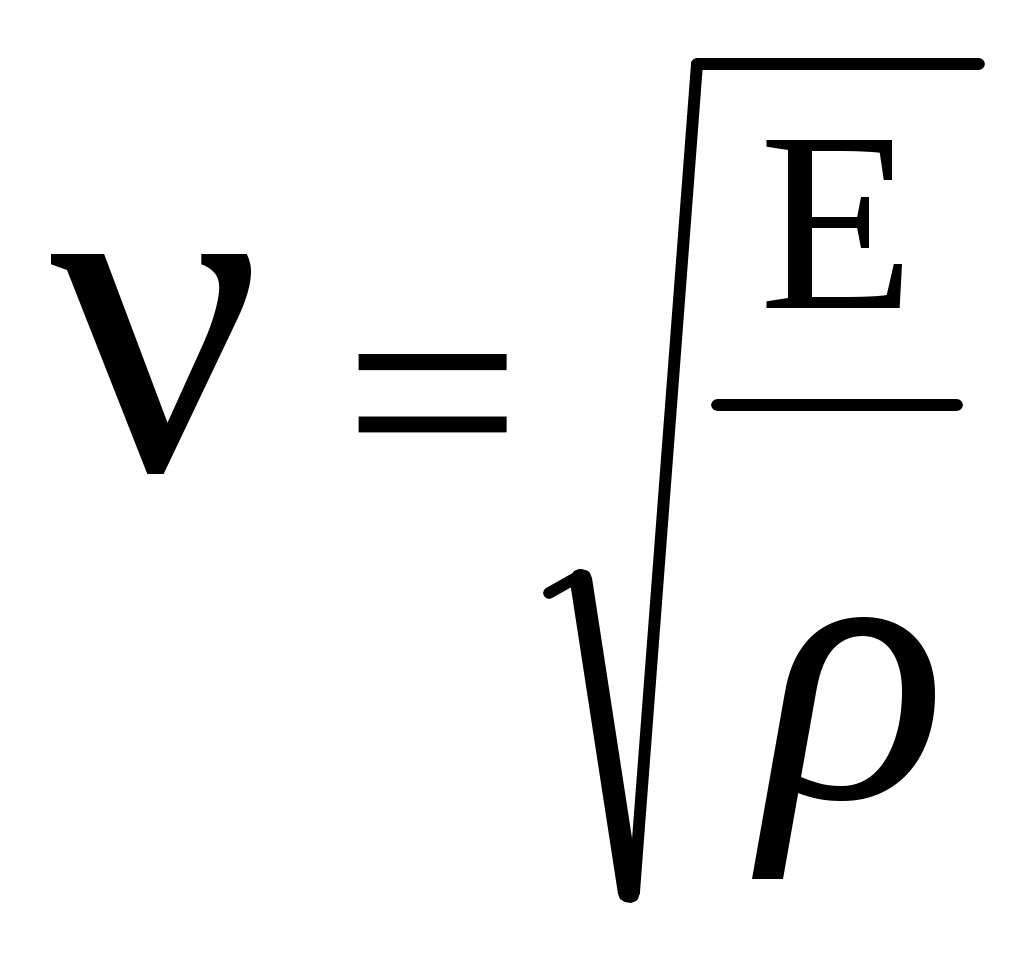 ,
,то для
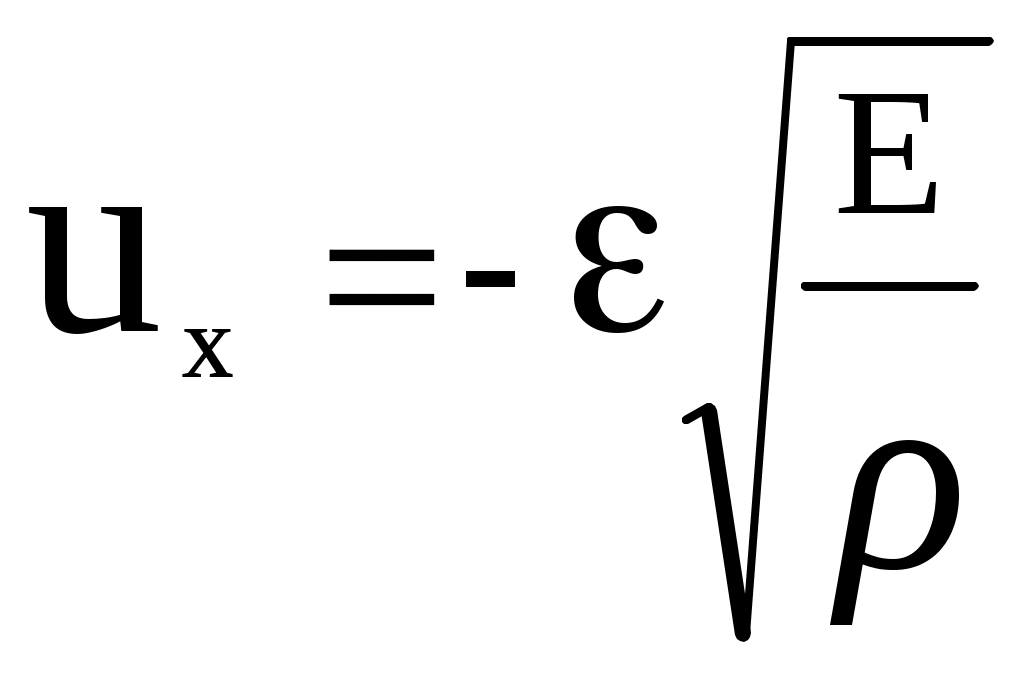 .
.Подставляя данные из условия задачи:
получаем:
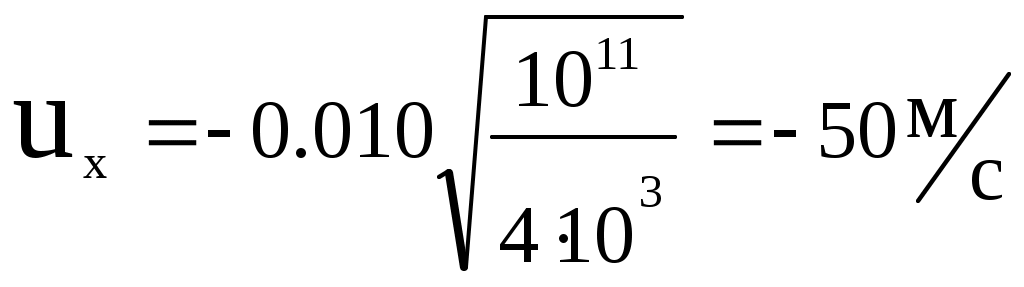 .
.-
Какое нормальное напряжение σn необходимо приложить к концам алюминиевого стержня, чтобы при его нагревании на ∆Т=1К длина стержня не изменилась? Коэффициент линейного растяжения алюминия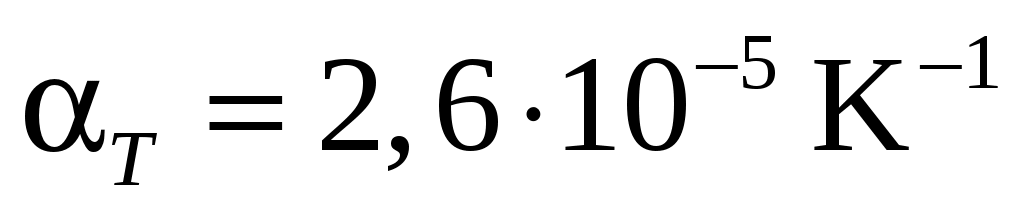 ,( модуль Юнга для алюминия Е=6,9
,( модуль Юнга для алюминия Е=6,9 1010Па.
1010Па.
Решение
Согласно закону линейного теплового расширения кристаллов относительное изменение длины
| | (3.1) |
В соответствии с законом Гука для однородного стержня такая деформация наблюдается при приложении к концам стержня растягивающего усилия с нормальным напряжением
| | (3.2) |
где Е – модуль Юнга материала стержня.
Из формул (3.1) и (3.2) следует, что для предотвращения теплового расширения стержня к его концам необходимо приложить сжимающее усилие с нормальным напряжением
| | (3.3) |
Ответ:
Таблица 1 – Варианты заданий для решения Пример№1
| Вариант | | ∆Т=1К | Е=6,9 |
| 1 | 2,8 | 2 | = |
| 2 | 2,9 | 4 | = |
| 3 | 3 | 6 | = |
| 4 | 2,5 | 8 | = |
| 5 | 2,4 | 10 | = |
| 6 | 2,8 | 1 | = |
| 7 | 2,8 | 12 | = |
| 8 | 2,9 | 2 | = |
| 9 | 3 | 4 | = |
| 10 | 2,5 | 6 | = |
| 11 | 2,4 | 8 | = |
| 12 | 2,8 | 10 | = |
| 13 | 2,8 | 1 | = |
| 14 | 2,9 | 12 | = |
Вопросы к практическому занятию:
Напишите конспективно ответы на вопросы:
Вопрос 1. Какие бывают деформации?
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Вопрос 3. Как направлена сила упругости?
Вопрос 4. Какую природу имеет сила упругости?
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?