Файл: Пространственная решетка и ее свойства.doc

ФИЗИКА ТВЕРДОГО ТЕЛА

Оглавление

Введение 3

1. Пространственная решетка и ее свойства 5

1.1. Элементарные ячейки и структура кристаллов 5

Задачи для самостоятельных и домашних работ 11

1.2. Плоскости в кристаллической решетке. Индексы Миллера 13

Задачи для самостоятельных и домашних работ 17

1.3. Обратная решетка и ее свойства. 18

Задачи для самостоятельных и домашних работ 23

2. 
   Дифракция рентгеновских лучей в кристаллах. Формула Вульфа-Брэгга. 23
   

Задачи для самостоятельных и домашних работ 27

3. Межатомные взаимодействия и типы связей в твердых телах 29

Задачи для самостоятельных и домашних работ 34

4. Дефекты в кристаллах, диффузия. 37

Задачи для самостоятельных и домашних работ. 41

5. Динамика кристаллической решетки. 43

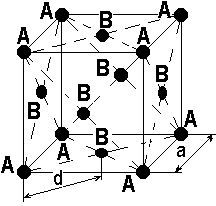
Пространственная решетка и ее свойства

7. Элементарные ячейки и структура кристаллов

Задача 1. Плотность кристалла NaC1 равна 2180 кг/м³. Атомный вес натрия 23, хлора 35,46. Определить постоянную решетки.

Решение. Масса элементарной ячейки кристалла NaCl равна M=a³

где a – постоянная решетки,  – плотность кристалла. Но, с другой стороны,

13. 
    = m_H (N_NaA_Na + N_ClA_Cl)
    

где m_H – масса атома водорода (1,6610^-27 кг); N_Na – число атомов натрия в элементарной ячейке; N_Cl – число атомов хлора в элементарной ячейке; A_Na – атомный вес натрия; A_Cl –атомный вес хлора.

Приравнивая правые части двух выражений и учитывая, что на одну элементарную ячейку NaC1 приходится половина атома натрия и половина атома хлора, получаем





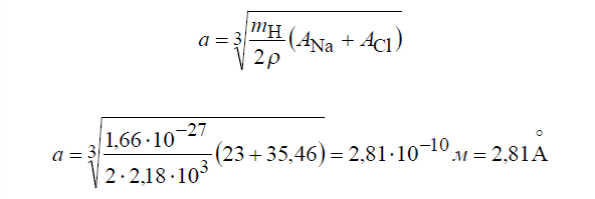
Задача 2. Найти число атомов алюминия в единице объема. Плотность алюминия  =2700 кг/м³.

Решение.

---

В килограмм-молекуле алюминия содержится 6,0210²⁶ атомов.

Одна килограмм-молекула занимает объем:

V₁=A/

где A – атомный вес,  – плотность . Тогда число атомов в единице объема:



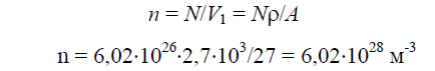
Задача 4 (6). Определить объемы элементарной ячейки через радиусы

равновеликих шаров, образующих плотные упаковки для 1) объемно-

центрированной, 2) гранецентрированной и 3) гексагональной решеток.

Решение. 1) Параметр элементарной ячейки через

радиус шара выражается следующим образом (рис. 2):







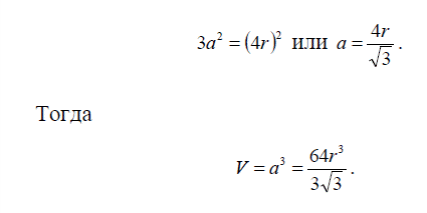
Задача 5 (7). Чему равно число атомов в элементарной ячейке в случае 1)

простой, 2) объемноцентрированной и 3) гранецентрированной кубических

решеток?

Решение. 1) В простой кубической решетке атомы находятся только в

вершинах углов ячейки. Одна вершина принадлежит восьми

параллелепипедам кристаллической решетки. Поэтому на каждую вершину

одной ячейки приходится одна восьмая часть атома, находящегося в вершине

(рис. 4а).



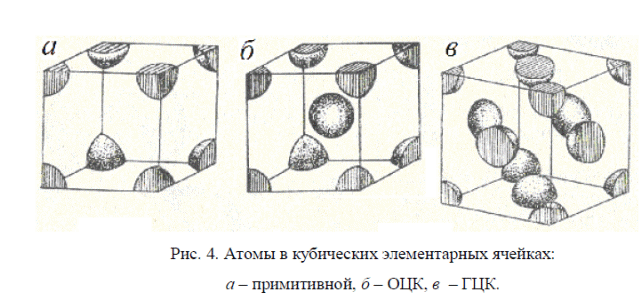
Ячейка имеет восемь углов, следовательно, на нее приходится один атом.

2) В объемноцентрированной кубической решетке, кроме атомов,

расположенных в углах, элементарной ячейке принадлежит полностью

внутренний центральный атом (рис. 4б). Таким образом, в объемно-

центрированной решетке на каждую ячейку приходится два атома.

3) В гранецентрированной кубической решетке атомы, расположенные

в центре граней, принадлежат двум ячейкам (рис. 4в). Поэтому число атомов

в элементарной ячейке равно четырем.

Задача 6 (8). Чему равно число атомов в элементарной ячейке

гексагональной плотноупакованной решетки?

Решение. На элементарную ячейку в гексагональной плотноупакованной решетке приходится шесть атомов. Три внутренних атома, которые расположены в центрах трех (из шести) тригональных призм (рис. 5), полностью принадлежат одной элементарной ячейке.

---

Два атома, расположенные в центрах базисных граней, принадлежат элементарной ячейке наполовину и в сумме дают один атом. Каждый атом, который находится в вершине гексагональной призмы, принадлежит шести элементарным ячейкам.

В целом все эти двенадцать атомов вносят вклад в одну элементарную

ячейку на два атома. Итак, на элементарную ячейку гексагональной решетки

приходится шесть атомов.



Задача 8 (12). Пусть гранецентрированная кубическая и гексагональная

решетки построены из одинаковых атомов, представляющих собой жесткие

сферы с радиусом r. Показать, что часть объема, занятая атомами при таком

расположении, равна

Решение. Для гранецентрированной кубической решетки N=4, объем

элементарной ячейки равен .

Тогда

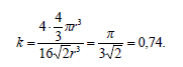
Поскольку в элементарной ячейке гексагональной решетки содержится

шесть атомов, то коэффициент заполнения пространства определяется

выражением



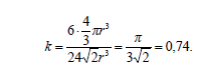
Таким образом, в гексагональной решетке, равно как и в гранецентрированной кубической, атомами заполнено всего лишь 74% пространства от общего объема решетки.

Из приведенных вычислений следует, что даже в решетках с самой плотной упаковкой атомов остаются незаполненными 26% пространства от общего объема решетки.

Задача 9 (22). Вычислить объем элементарной ячейки триаминхлорида четырехвалентной платины, если параметры ячейки и углы триклинности



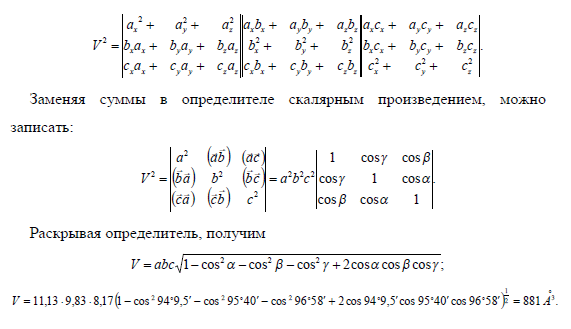
Задача 10 (23). Воспользовавшись формулой объема элементарной ячейки

триклинной системы, получить формулы для объема ячеек 1) моноклинной,

2) гексагональной и 3) ромбоэдрической систем.

---

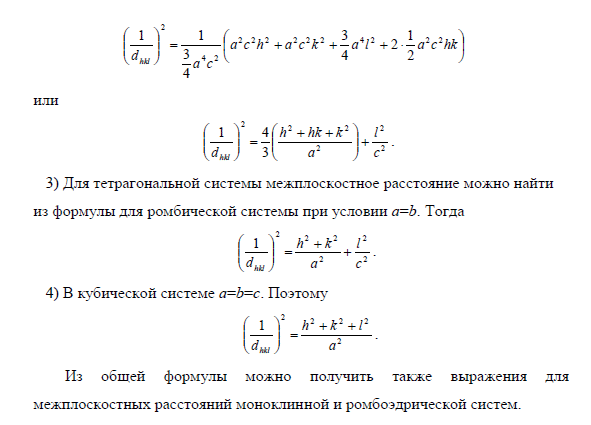
Механические свойства твёрдых тел

Задача 1

Оценить постоянную решетки и расстояние d между ближайшими атомами для меди. Атомы меди образуют гранецентрированную кубическую решетку, плотность кг/м³, молярная масса кг/моль.

Анализ и решение

В гранецентрированной кубической (ГЦК) решетке, кроме узлов А (их вклад в ячейку атому, (см. задачу 16), имеются узлы в середине каждой грани (узлы B). Таких

узлов B в ячейке 6 (по числу граней). Каждый из них принадлежит двум смежным ячейкам, следовательно, его вклад в одну ячейку равен , а вклад всех 6 узлов составляет . Таким образом, в ГЦК- структуре на долю одной ячейки приходится атома.

Объём одной ячейки равен ³, где - ребро куба(и постоянная решетки). Тогда на долю одной частицы приходится объёма ячейки.

Масса одного атома меди 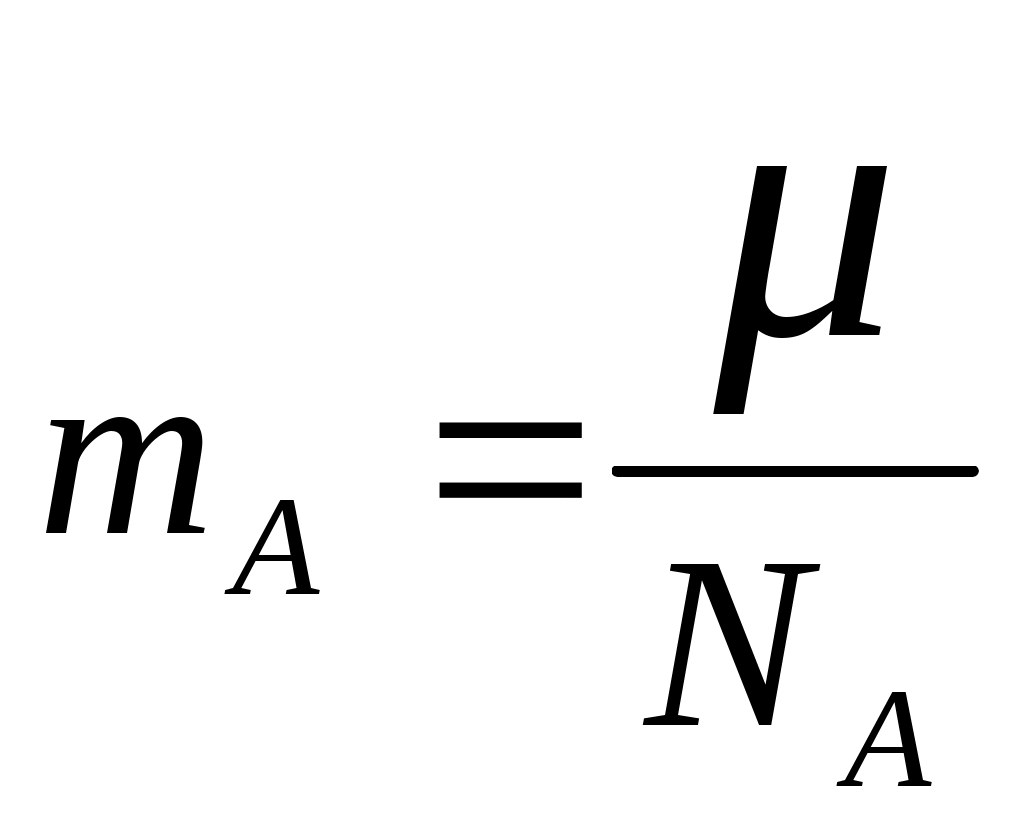, где N_A - число Авогадро.

Плотность меди: ,

---

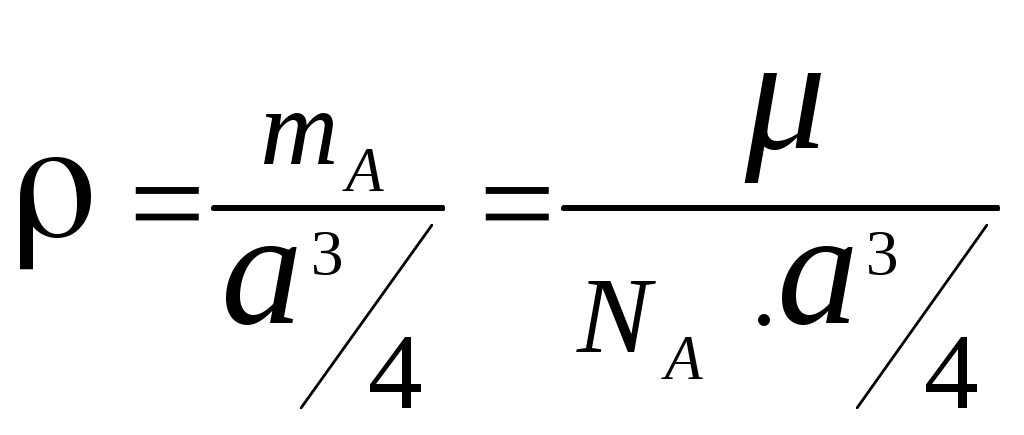Отсюда: , или Å

Наименьшим расстоянием dмежду атомами в ГЦК - структуре будет расстояние между атомами, один из которых находится в вершине, а другой в центре грани, поэтому

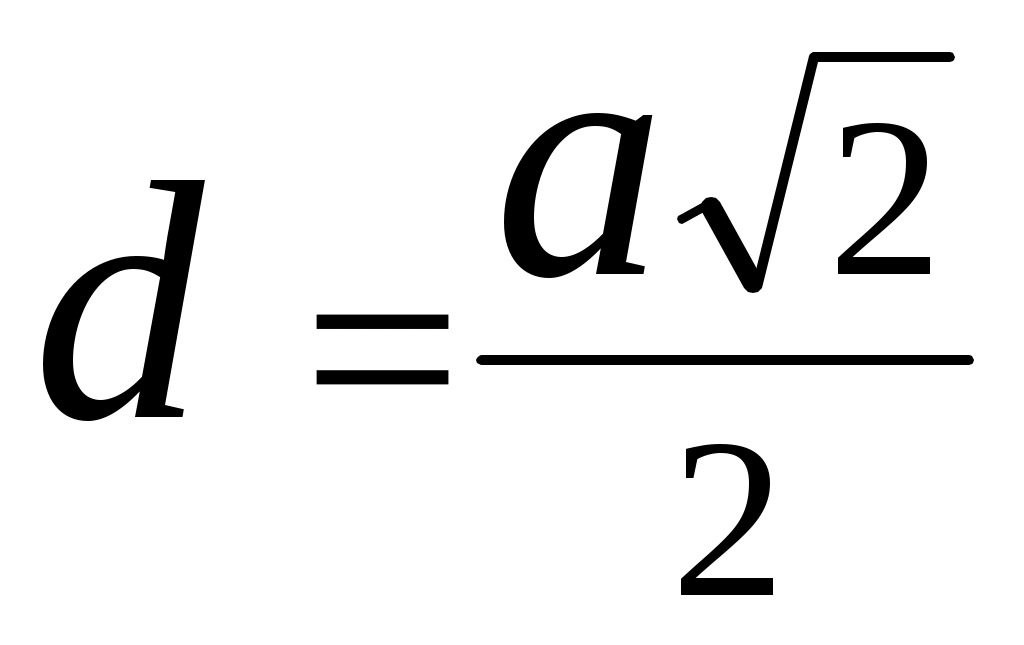, отсюда Å.

Задача 2

С 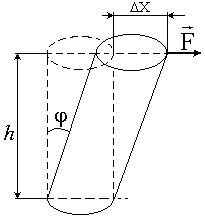равните величину относительной деформации φ (угол сдвига) и смещения верхнего основания двух цилиндров одинаковых размеров, сделанных один из чугуна, а другой из свинца, если на верхнее основание каждого (вдоль него) действует одна и та же сила, а нижние основания закреплены. Какой из этих материалов вы бы предпочли для изготовления болтов?

Анализ и решение

При деформации сдвигом, все плоские слои твердого тела, параллельные некоторой плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. Сдвиг происходит под действием силы F, приложенной касательно к верхнему основанию цилиндра, параллельно плоскости сдвига. Мерой деформации является угол сдвига φ (относительный сдвиг), выраженный в радианах.



Для малых углов , поэтому (1) определит смещение верхнего основания цилиндра (абсолютный сдвиг). При деформации произошло смещение частиц, находящихся в узлах кристаллической решетки твердого тела, из первоначальных положений равновесия в новые. Такому смещению будут препятствовать силы взаимодействия между частицами, поэтому в деформированном теле возникают внутренние упругие силы, уравновешивающие внешние силы, приложенные к телу. Упругие силы вызывают внутренние напряжения, определяемые отношением упругой силы F_упр к площади сечений тела:

---