ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 89
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
; q=
III. Подведение итогов.
Домашнее задание:
№ 21 ( 4), № 22 (2), № 23 (2).
Математика 10 класс Дата ___________
Тема: АРИФМЕТИЧЕСКИЙ КОРЕНЬ НАТУРАЛЬНОЙ СТЕПЕНИ
Цели:
1) Знать определение арифметического корня натуральной степени, свойства корня п-й степени.
2) Развивать практические умения и навыки учащихся.
3) Воспитывать чувство коллективизма, умение работать в парах
Ход урока
Проверка домашнего задания
Решим уравнение:
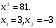
Итак, уравнение имеет два действительных корня ( корни 4-ой степени из числа 81).
Положительный корень из числа 81 называют арифметическим корнем четвертой степени из числа 81.
Т.о.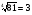 .
.
ОПР. Арифметическим корнем натуральной степени n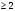 из неотрицательного числа а называется неотрицательное число, n-ая степень которго равна а.
из неотрицательного числа а называется неотрицательное число, n-ая степень которго равна а.
a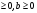 :
: 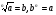 .
.
Арифметический корень 2-ой степени- квадратный корень, 3-ей степени- кубический.
Рассотрим свойства арифметического корня натуральной степени:
n-четное n=2k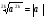
№27
№28, 29
№ 32 (1; 3; 5)-
№ 33-36 (1,3)
№33 1)3,5; 3)20;
№34 1)35; 3) 1,6;
№ 35 1) 10; 3) 6;
№36 1)72; 3) 3.
№ 42, № 43 (1, 3
№42(1):
V. Домашнее задание: № 32 (2,4,6), № 42 (2,4
VI. Итог урока. Вопросы по теории:
.
Математика 10 класс Дата ___________
Тема: АРИФМЕТИЧЕСКИЙ КОРЕНЬ НАТУРАЛЬНОЙ СТЕПЕНИ
Цели:
1) уметь применять свойства арифметического корня при решении задач
2) Развивать практические умения и навыки учащихся.
3) Воспитывать положительную мотивацию к изучаемому предмету
Ход урока
I. Организационный момент
Проверка домашнего задания
II. Практическая часть
№34 № 35 №36
№ 42, № 43 (1, 3) №42(1):
III. Домашнее задание: ), № 43 (2,4), № 50.
Математика 10 класс Дата ___________
Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ
ПОКАЗАТЕЛЕМ
Цели:
1) Знать определение степени с рациональным показателем, свойства этой степени;
2)Развивать практические умения и навыки учащихся.
3) Воспитывать положительную мотивацию к изучаемому предмету


III. Практическая часть.
№55,
№56
№ 55 (1)
№56 (1)
№ 60 (1)
IV. Домашнее задание: № 69 (2), № 70 (2, 4), № 85 (2,4).
V. Итог урока. Что нового узнали на уроке?
(В виде беседы с классом.)
Математика 10 класс Дата ___________
Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
Цели:
1) определение степени с действительным показателем, теорему и три следствия из нее
2) воспитание коммуникативной и информационной культуры обучающихся;
Ход урока
I. Организационный момент
Проверка домашнего задания
II. Практическая часть
вычислим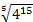
Мы можем представить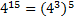 , тогда
, тогда
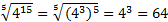
Таким образом, мы можем записать
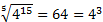 или
или 
На основании данного примера можно сделать вывод:
Если n- натуральное число,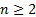 , m- целое число и частное
, m- целое число и частное 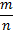 является целым числом, то при
является целым числом, то при 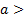 0 справедливо равенство:
0 справедливо равенство:
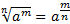 .
.
Напомним, что r-рациональное число вида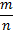 , где m- целое число , n- натуральное число. Тогда по нашей формуле получим:
, где m- целое число , n- натуральное число. Тогда по нашей формуле получим:
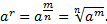
Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.
Если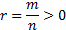 , то выражение
, то выражение 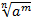 имеет смысл не только при
имеет смысл не только при 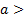 0, но и при а=0, причем,
0, но и при а=0, причем, 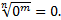 Поэтому считают, что при r
Поэтому считают, что при r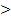 0 выполняется равенство
0 выполняется равенство 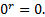
Пользуясь формулой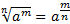
степень с рациональным показателем можно представить в виде корня и наоборот.
№ 70 (3)
№71 (1-3)
№72, № 73
№76
III. . Домашнее задание:
№ 71 (2, 4), № 79
Математика 10 класс Дата ___________
Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
Цели:
1) уметь выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем
2) развитие навыка само- и взаимоконтроля; развитие интеллектуальных способностей, мыслительных умений,
3) воспитание познавательного интереса к предмету, воспитание ответственности за выполняемую работу, способствовать созданию атмосферы активного творческого труда.
Ход урока
I. Организационный момент
Проверка домашнего задания
II. Практическая часть
Учащиеся у доски - разбор упражнений из учебника
№70. № 80, №82, №83
III. Домашнее задание
№96(2,6), №103(2,4), №110
Математика 10 класс Дата ___________
Тема: Решение задач по теме действительные числа
Цели:
1) что такое натуральное, целое, рациональное число, иррациональное число действительные числа, периодическая дробь; вспомнить правила записи бесконечной десятичной дроби в виде обыкновенной, повторить особенности бесконечно убывающей геометрической прогрессии, обобщить правила работы со степенями.
2) Развивать навыки и умения, в выполнении заданий по теме, умение работать в группе и самостоятельно.
3) Воспитывать интерес к математике путём введения разных видов закрепления материала
Ход урока:
1. Организационный момент
Проверка домашнего задания
II. Практическая часть
1) Множества чисел
Какова взаимосвязь множества чисел?
СМА ВЫБОР
Соотнести число с множеством - работа в группах
СМА ПРОТИВОРЕЧИЕ
Определить допущенную ошибку
2) периодические десятичные дроби
Какая дробь называется бесконечной периодической?
Работа у доски - №93(1,3)
Работа в группах - №93(2,4)
3) Бесконечно убывающая геометрическая прогрессия
III. Подведение итогов.
Домашнее задание:
№ 21 ( 4), № 22 (2), № 23 (2).
Математика 10 класс Дата ___________
Тема: АРИФМЕТИЧЕСКИЙ КОРЕНЬ НАТУРАЛЬНОЙ СТЕПЕНИ
Цели:
1) Знать определение арифметического корня натуральной степени, свойства корня п-й степени.
2) Развивать практические умения и навыки учащихся.
3) Воспитывать чувство коллективизма, умение работать в парах
Ход урока
-
Организационный момент.
Проверка домашнего задания
-
Теоретическая часть.
Решим уравнение:
Итак, уравнение имеет два действительных корня ( корни 4-ой степени из числа 81).
Положительный корень из числа 81 называют арифметическим корнем четвертой степени из числа 81.
Т.о.
ОПР. Арифметическим корнем натуральной степени n
a
Арифметический корень 2-ой степени- квадратный корень, 3-ей степени- кубический.
Рассотрим свойства арифметического корня натуральной степени:
-
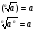 4)
4) 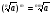
-
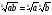 5)
5) 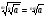
-
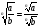 6) если n-нечет n=2k+1
6) если n-нечет n=2k+1 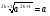
n-четное n=2k
-
Практическая часть.
№27
№28, 29
№ 32 (1; 3; 5)-
№ 33-36 (1,3)
№33 1)3,5; 3)20;
№34 1)35; 3) 1,6;
№ 35 1) 10; 3) 6;
№36 1)72; 3) 3.
№ 42, № 43 (1, 3
№42(1):
V. Домашнее задание: № 32 (2,4,6), № 42 (2,4
VI. Итог урока. Вопросы по теории:
-
Что такое арифметический корень натуральной степени? -
Какие свойства корня вы знаете?
.
Математика 10 класс Дата ___________
Тема: АРИФМЕТИЧЕСКИЙ КОРЕНЬ НАТУРАЛЬНОЙ СТЕПЕНИ
Цели:
1) уметь применять свойства арифметического корня при решении задач
2) Развивать практические умения и навыки учащихся.
3) Воспитывать положительную мотивацию к изучаемому предмету
Ход урока
I. Организационный момент
Проверка домашнего задания
II. Практическая часть
№34 № 35 №36
№ 42, № 43 (1, 3) №42(1):
III. Домашнее задание: ), № 43 (2,4), № 50.
Математика 10 класс Дата ___________
Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ
ПОКАЗАТЕЛЕМ
Цели:
1) Знать определение степени с рациональным показателем, свойства этой степени;
2)Развивать практические умения и навыки учащихся.
3) Воспитывать положительную мотивацию к изучаемому предмету


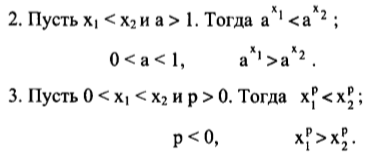
III. Практическая часть.
№55,
№56
№ 55 (1)
№56 (1)
№ 60 (1)
IV. Домашнее задание: № 69 (2), № 70 (2, 4), № 85 (2,4).
V. Итог урока. Что нового узнали на уроке?
(В виде беседы с классом.)
Математика 10 класс Дата ___________
Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
Цели:
1) определение степени с действительным показателем, теорему и три следствия из нее
2) воспитание коммуникативной и информационной культуры обучающихся;
-
3) эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради.
Ход урока
I. Организационный момент
Проверка домашнего задания
II. Практическая часть
вычислим
Мы можем представить
Таким образом, мы можем записать
На основании данного примера можно сделать вывод:
Если n- натуральное число,
Напомним, что r-рациональное число вида
Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.
Если
Пользуясь формулой
степень с рациональным показателем можно представить в виде корня и наоборот.
№ 70 (3)
№71 (1-3)
№72, № 73
№76
III. . Домашнее задание:
№ 71 (2, 4), № 79
Математика 10 класс Дата ___________
Тема: СТЕПЕНЬ С РАЦИОНАЛЬНЫМ И ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
Цели:
1) уметь выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем
2) развитие навыка само- и взаимоконтроля; развитие интеллектуальных способностей, мыслительных умений,
3) воспитание познавательного интереса к предмету, воспитание ответственности за выполняемую работу, способствовать созданию атмосферы активного творческого труда.
Ход урока
I. Организационный момент
Проверка домашнего задания
II. Практическая часть
Учащиеся у доски - разбор упражнений из учебника
№70. № 80, №82, №83
III. Домашнее задание
№96(2,6), №103(2,4), №110
Математика 10 класс Дата ___________
Тема: Решение задач по теме действительные числа
Цели:
1) что такое натуральное, целое, рациональное число, иррациональное число действительные числа, периодическая дробь; вспомнить правила записи бесконечной десятичной дроби в виде обыкновенной, повторить особенности бесконечно убывающей геометрической прогрессии, обобщить правила работы со степенями.
2) Развивать навыки и умения, в выполнении заданий по теме, умение работать в группе и самостоятельно.
3) Воспитывать интерес к математике путём введения разных видов закрепления материала
Ход урока:
1. Организационный момент
Проверка домашнего задания
II. Практическая часть
1) Множества чисел
Какова взаимосвязь множества чисел?
СМА ВЫБОР
Соотнести число с множеством - работа в группах
СМА ПРОТИВОРЕЧИЕ
Определить допущенную ошибку
2) периодические десятичные дроби
Какая дробь называется бесконечной периодической?
Работа у доски - №93(1,3)
Работа в группах - №93(2,4)
3) Бесконечно убывающая геометрическая прогрессия