Файл: Задача 1 Вычислить двойной интеграл от функции по заданной области . Решение Вид области представлен на рисунке.doc
Добавлен: 29.11.2023
Просмотров: 72
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
может принимать только два значения 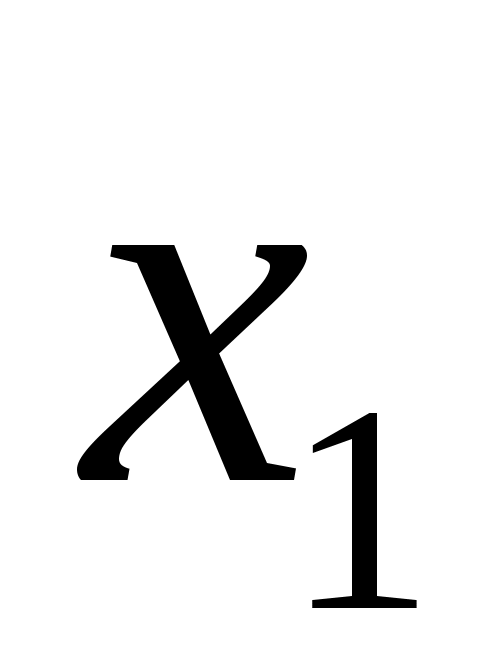 и
и 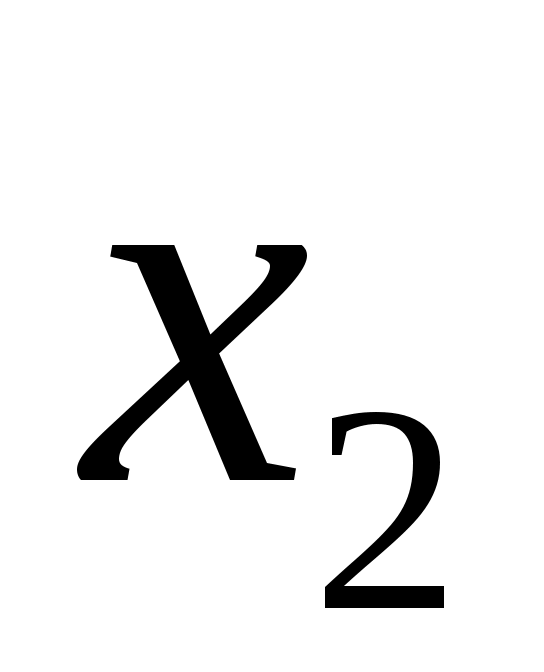 , причём
, причём 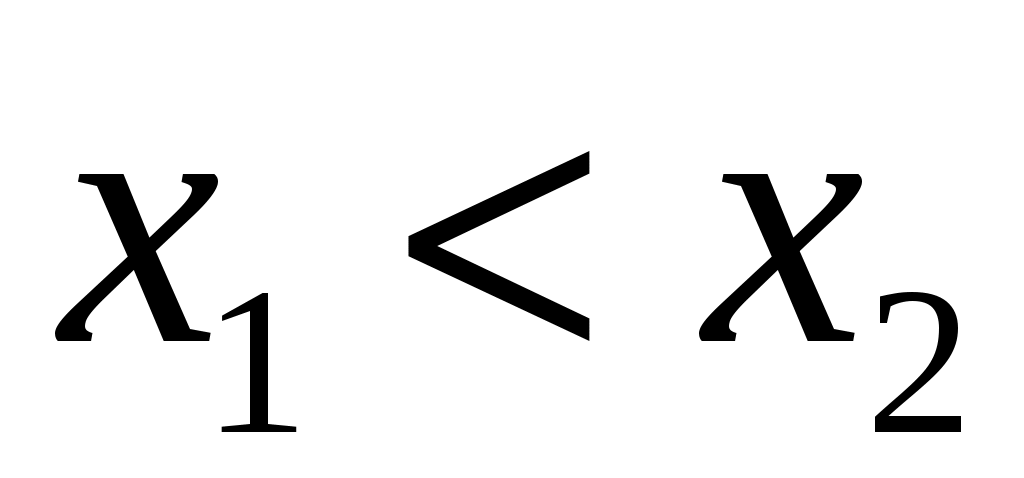 . Известны вероятность
. Известны вероятность 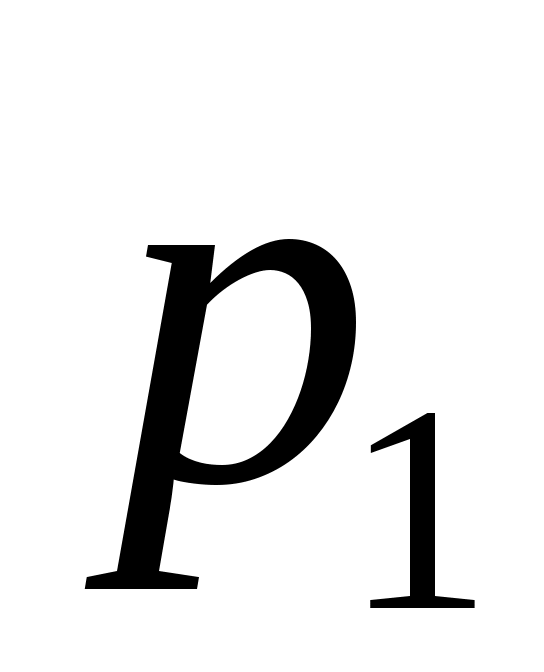 возможного значения
возможного значения 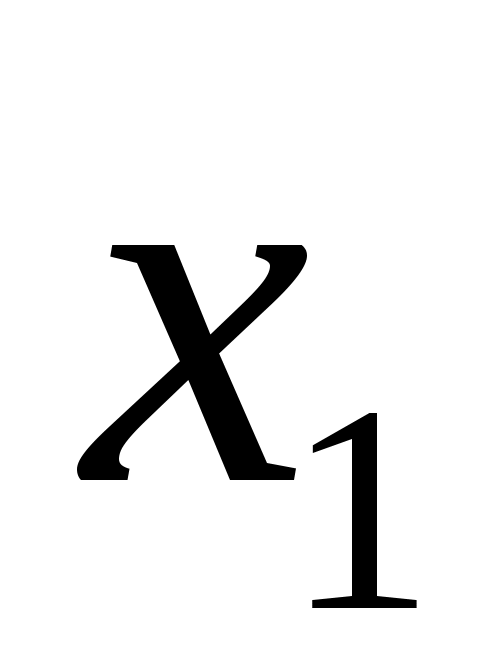 , математическое ожидание
, математическое ожидание 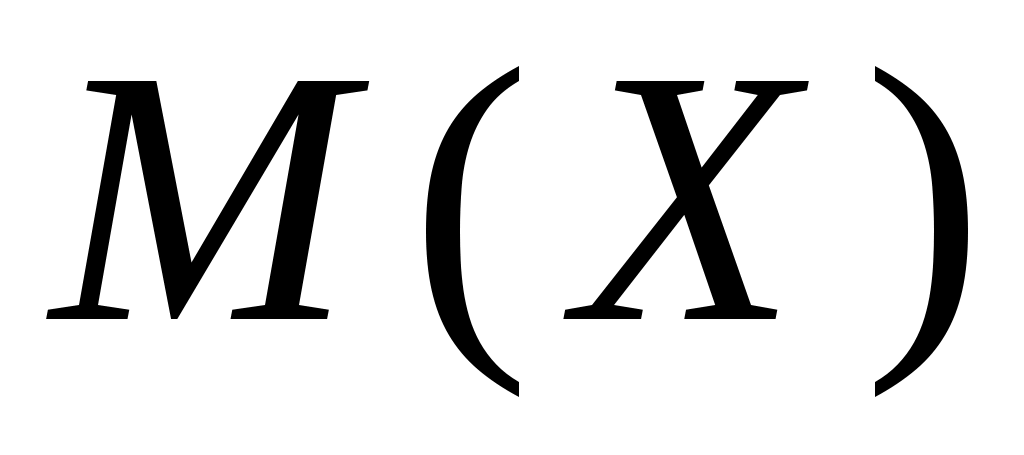 и дисперсия
и дисперсия 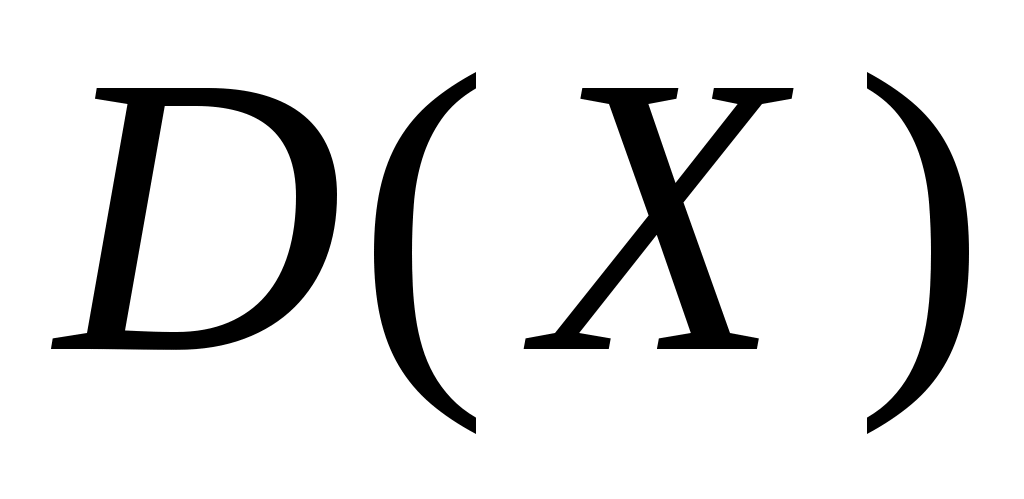 . Найти закон (ряд) распределения этой случайной величины.
. Найти закон (ряд) распределения этой случайной величины.
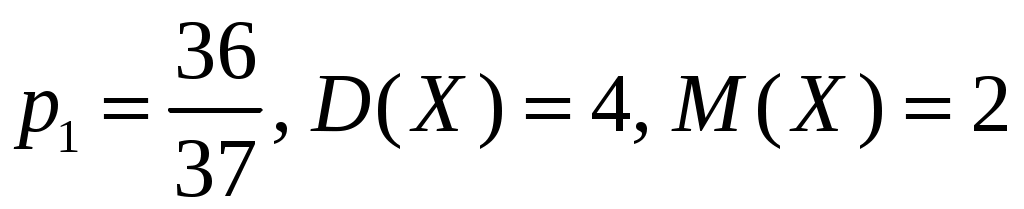 .
.
Решение
Сумма вероятностей всех возможных значений дискретной случайной величины должна быть равна единице, поэтому вероятность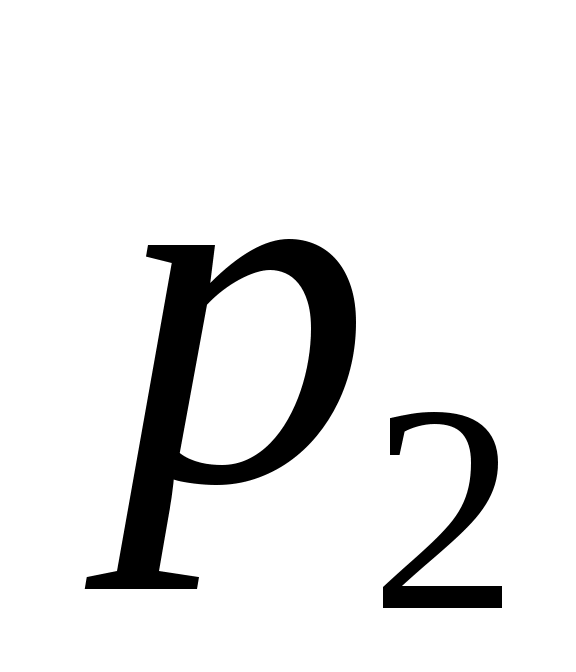 того, что
того, что  примет значение
примет значение 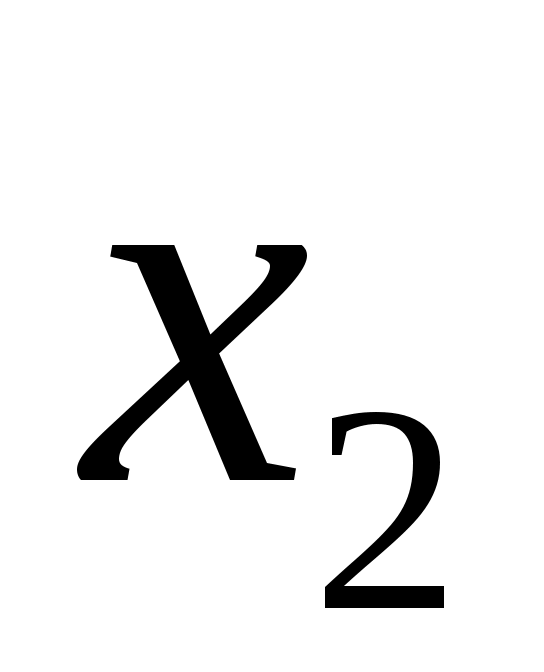 равна:
равна: 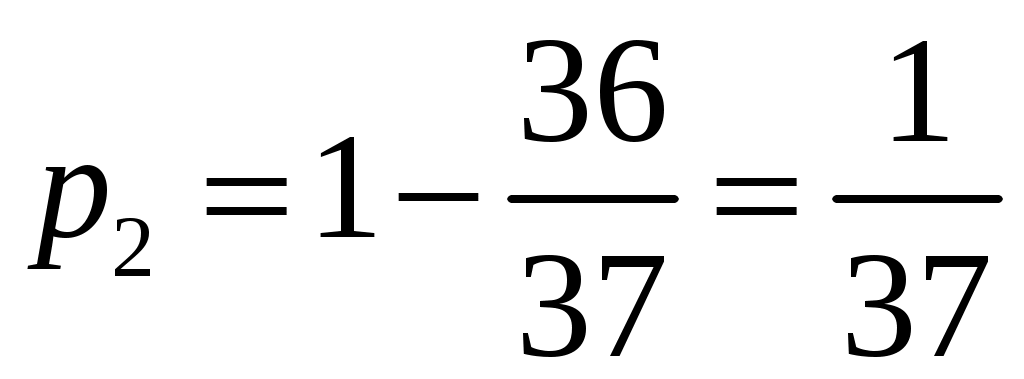 .
.
Тогда закон распределения :
:
По определению:
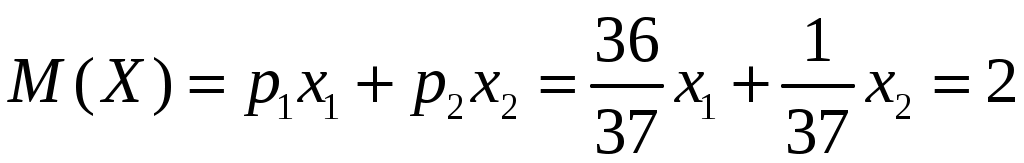 ;
;
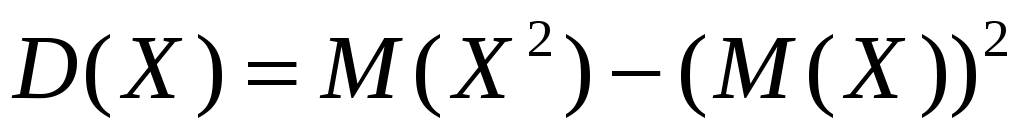 .
.
Напишем закон распределения
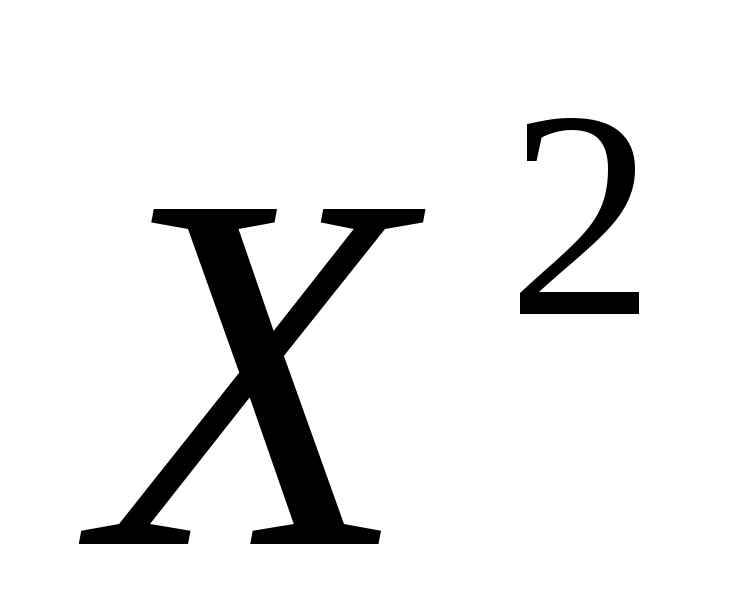 :
:
Найдём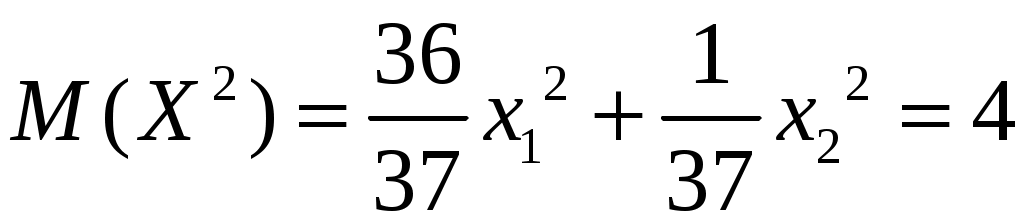 ,
,
тогда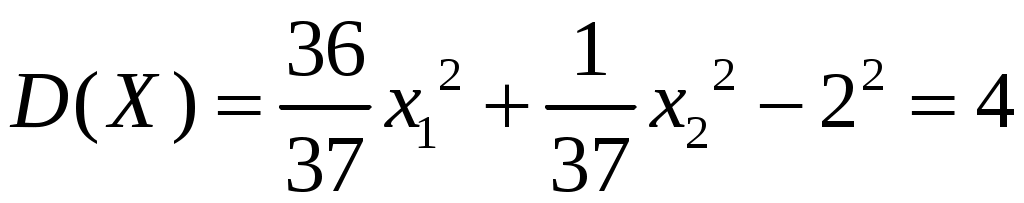 .
.
Имеем систему уравнений для нахождения и
и  :
:
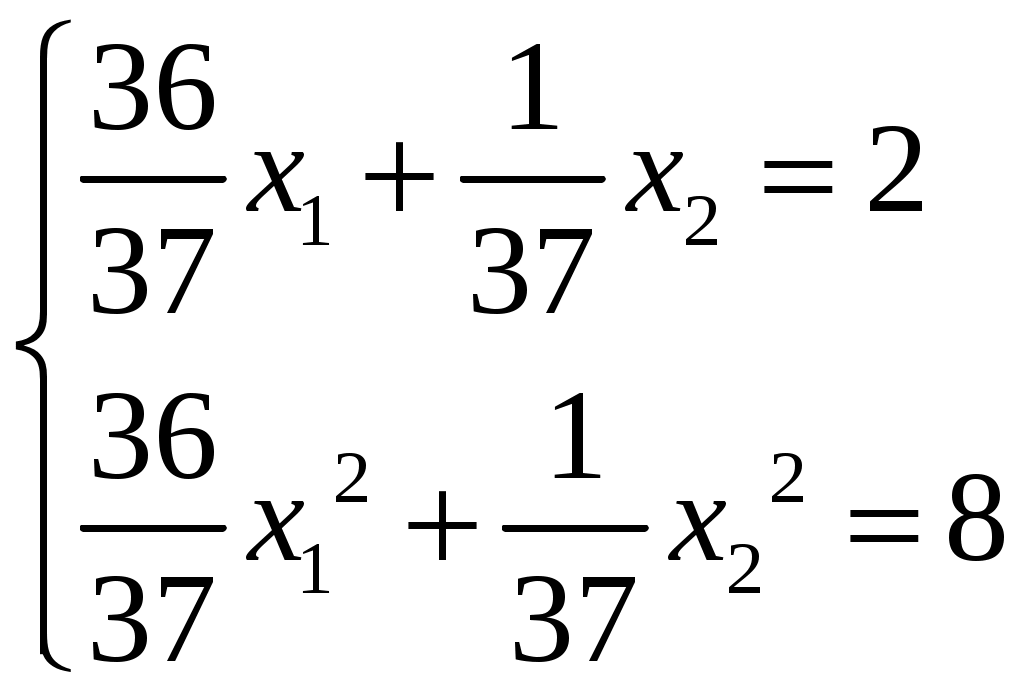 .
.
Решая систему, найдём: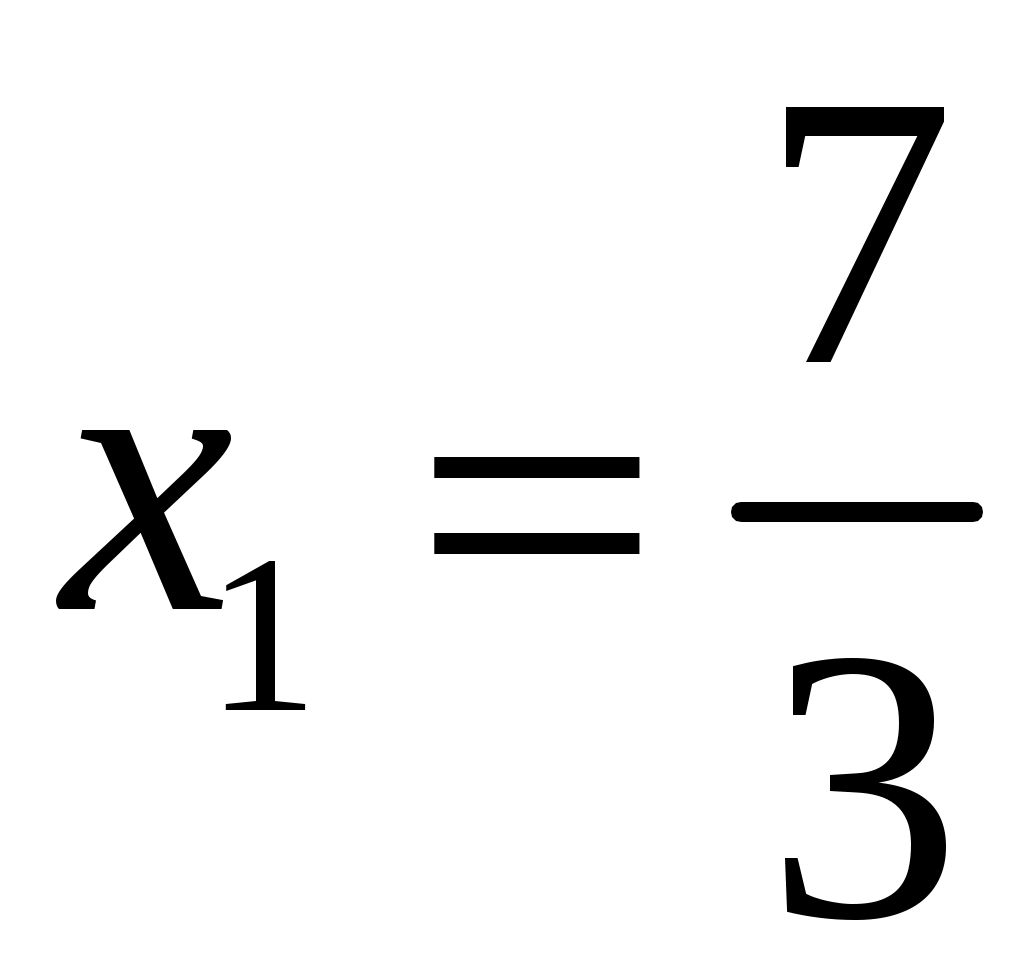 ,
, 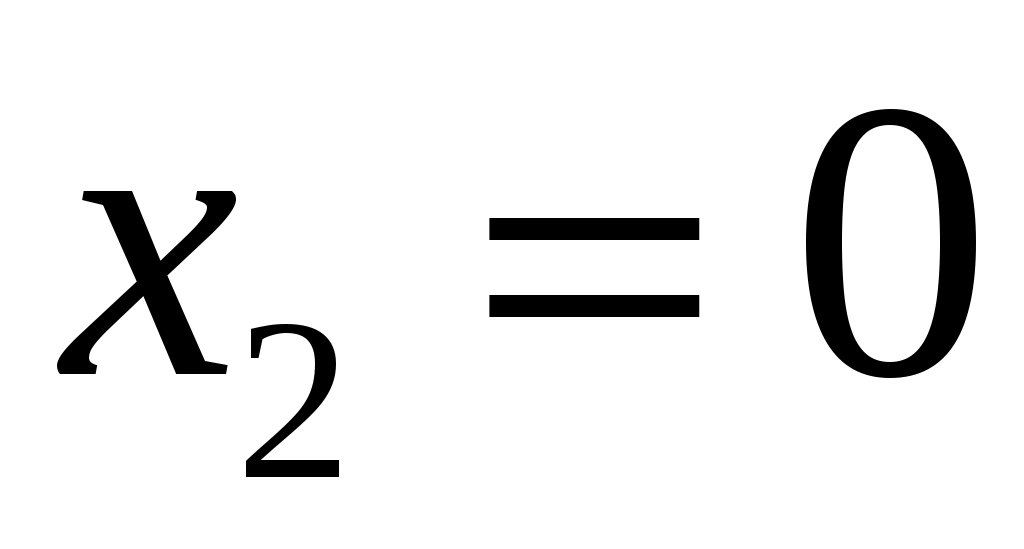 и
и 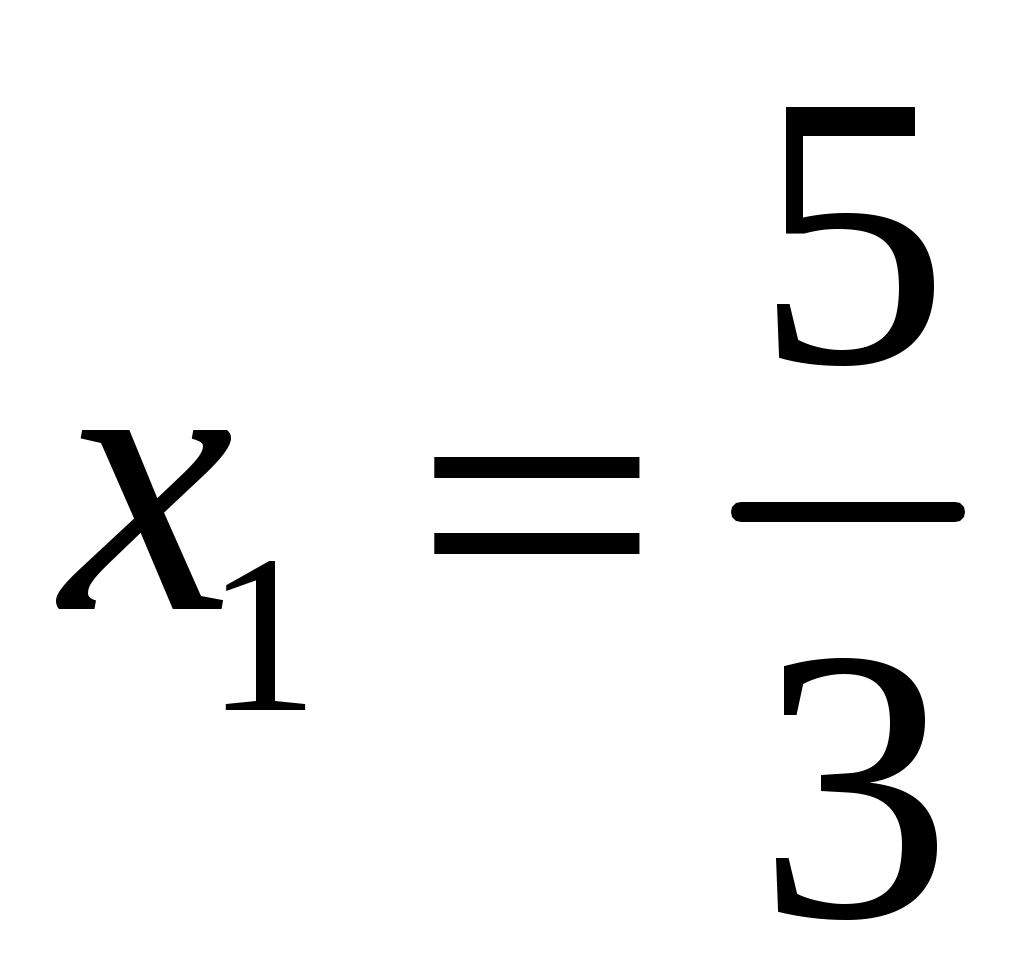 ,
, 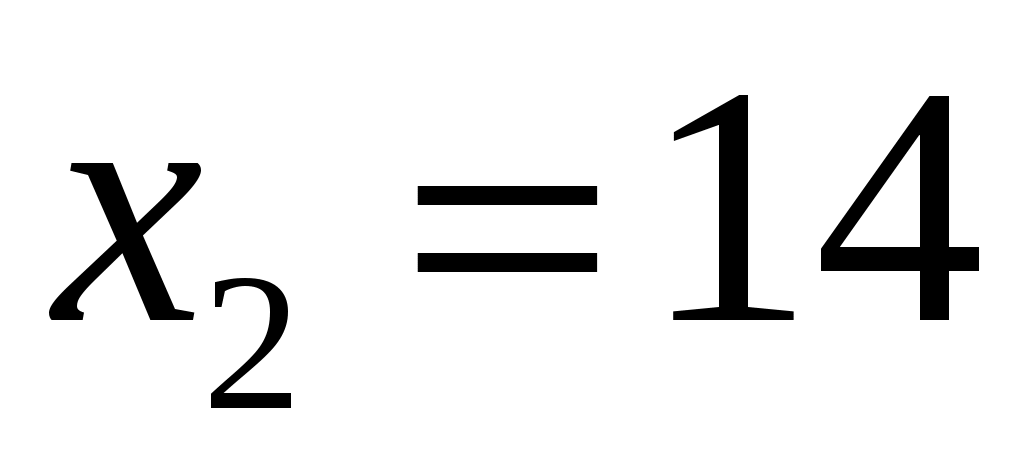 . По условию
. По условию  , поэтому первое решение не подходит. Тогда закон распределения дискретной случайной величины имеет вид:
, поэтому первое решение не подходит. Тогда закон распределения дискретной случайной величины имеет вид:
Задача №14
Случайная величина задана функцией распределения
задана функцией распределения 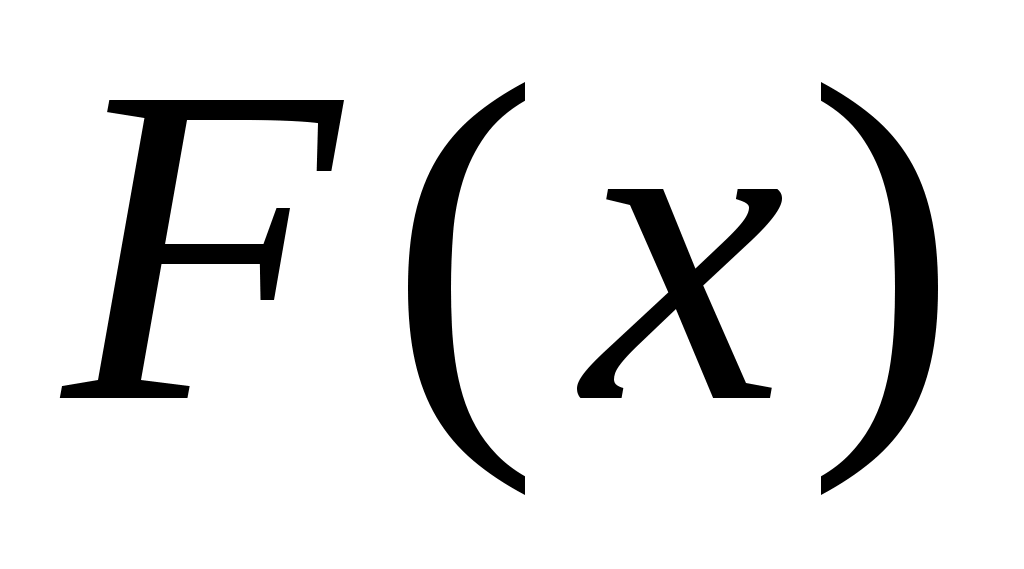 , требуется:
, требуется:
1) найти плотность вероятности;
2) математическое ожидание и дисперсию ;
;
3) построить графики функции распределения и функции плотности распределения.
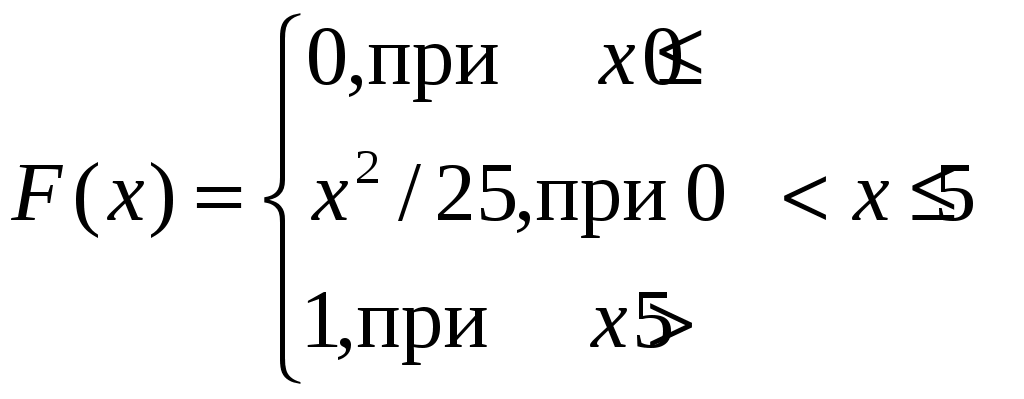 .
.
Решение
Найдём плотность распределения. По определению:
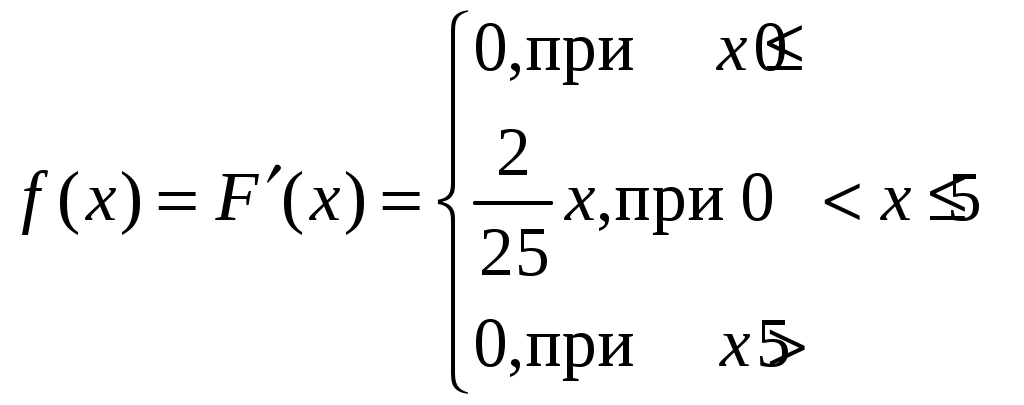 .
.
Тогда
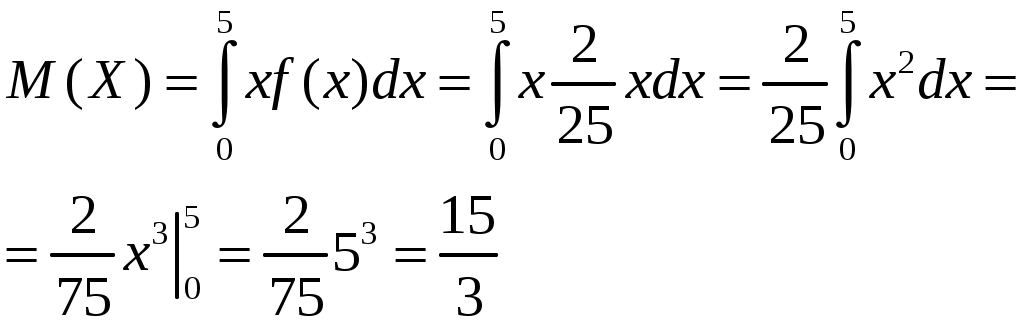 ,
,
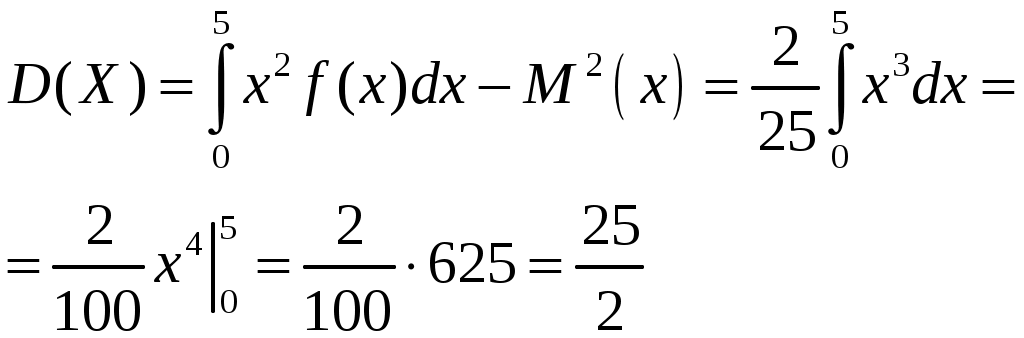 .
.
График функции распределения представлен на рисунке а)
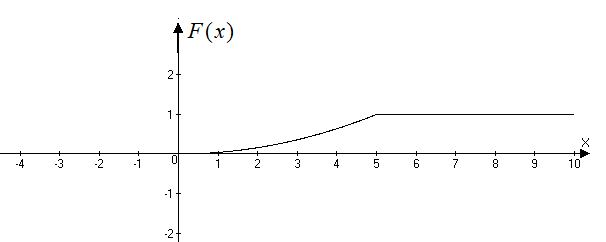
Рисунок а
График функции плотности распределения представлен на рисунке б).
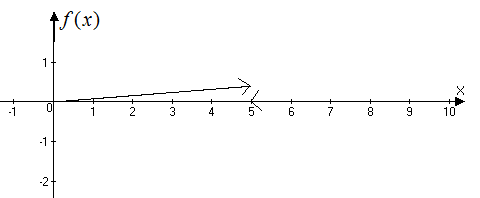
Рисунок б
Задача №15
Заданы математическое ожидание и средне квадратическое отклонение
и средне квадратическое отклонение  нормально распределённой величины
нормально распределённой величины  . Найти: 1) вероятность того, что
. Найти: 1) вероятность того, что  примет значение, принадлежащие интервалу
примет значение, принадлежащие интервалу 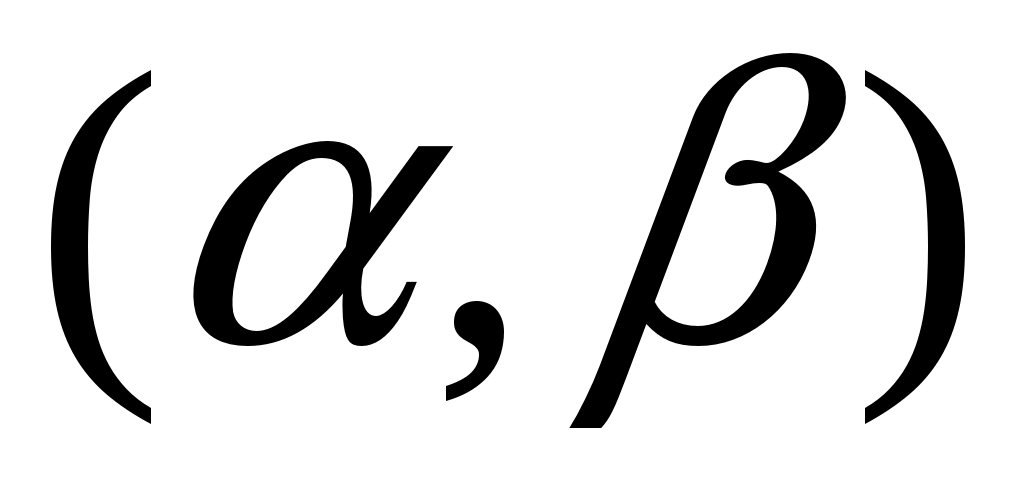 ; 2) вероятность того, что абсолютная величина отклонения
; 2) вероятность того, что абсолютная величина отклонения 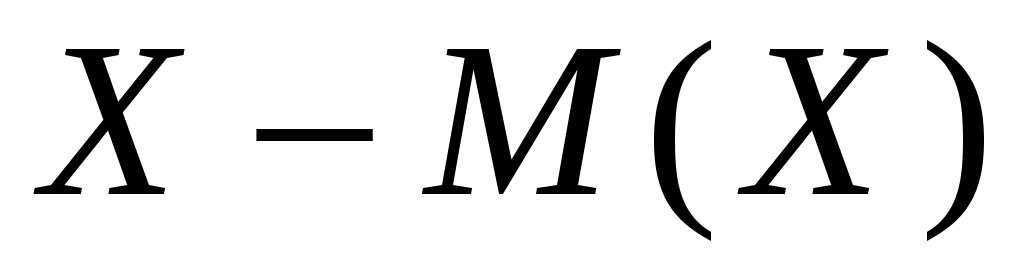 окажется меньше
окажется меньше 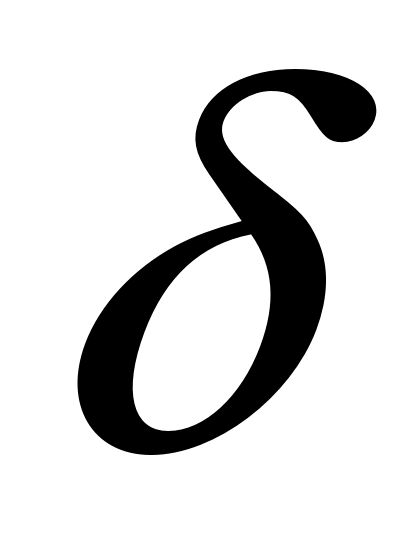 .
.
 .
.
Решение
1) Воспользуемся формулой:
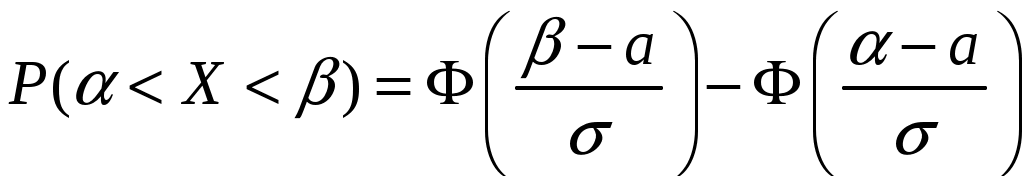 ,
,
подставив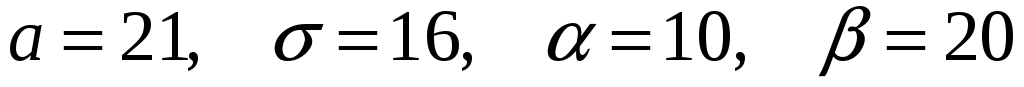
, получим:
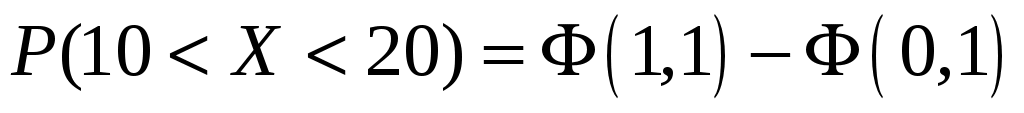 .
.
По таблицам приложения находим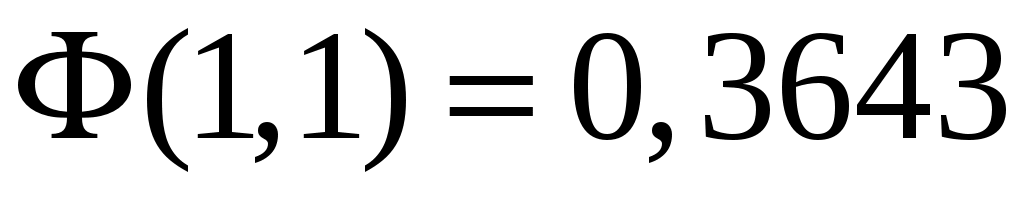 ;
; 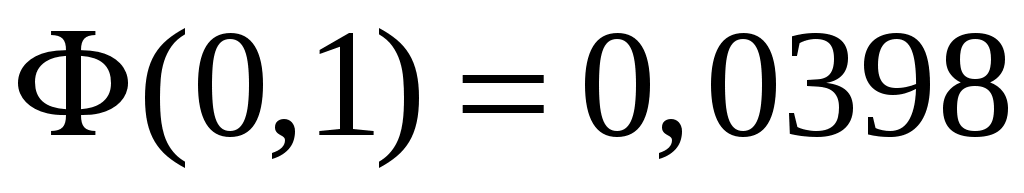 . Тогда искомая вероятность равна:
. Тогда искомая вероятность равна:
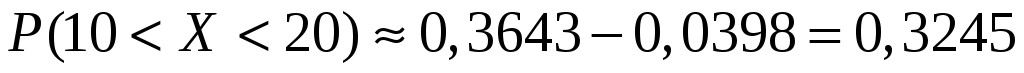 .
.
2) Искомая вероятность находится по формуле:
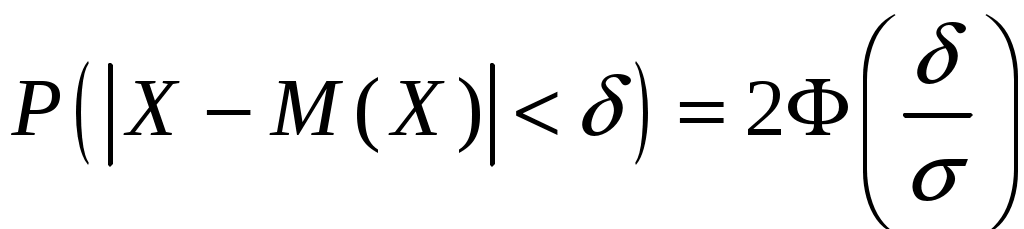 .
.
По условию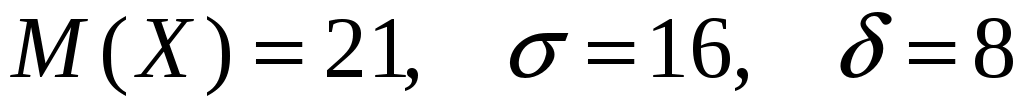 . Следовательно:
. Следовательно:
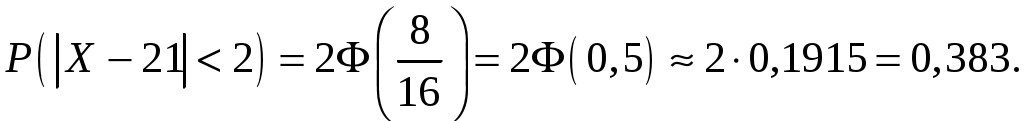
Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг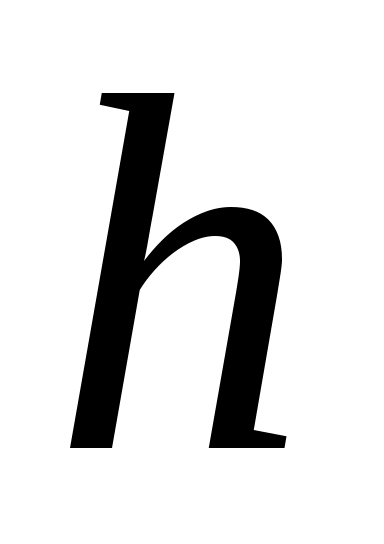 указан в варианте).
указан в варианте).
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность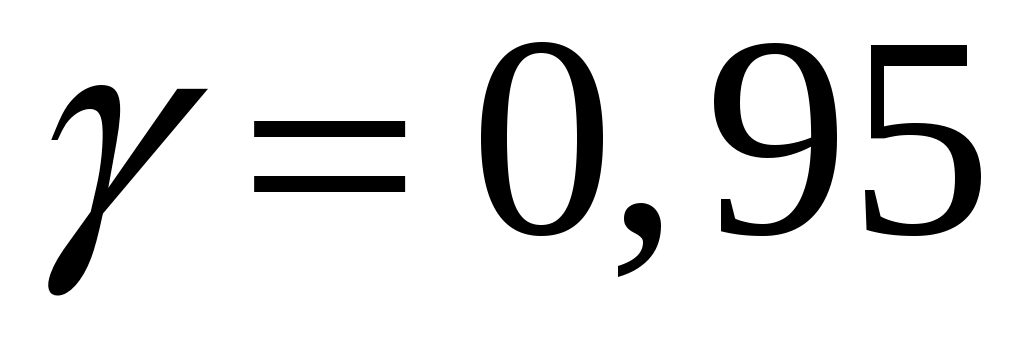 .
.
4) При уровне значимости =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
=0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
Выборка объёма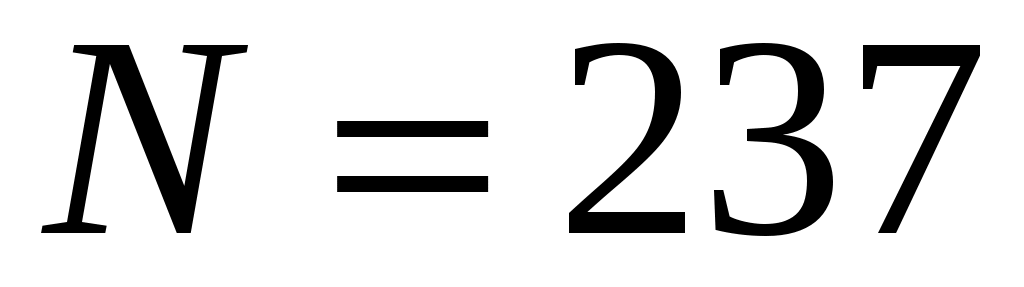 , начало первого интервала
, начало первого интервала 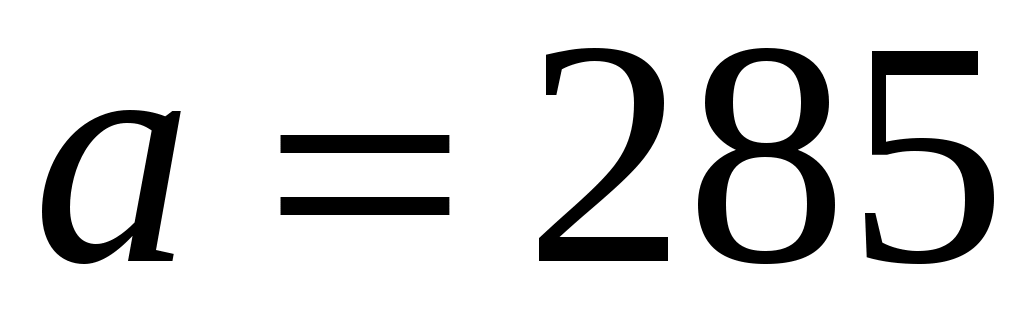 , шаг
, шаг 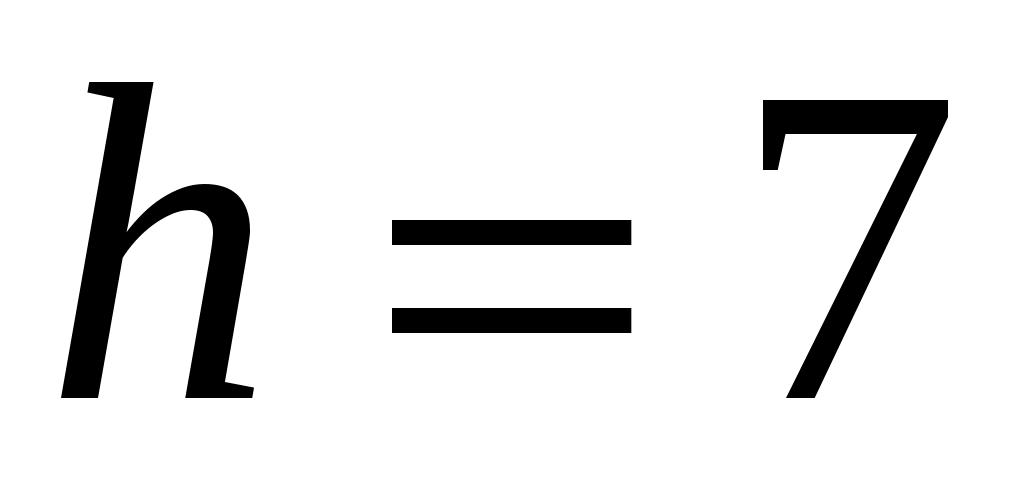 .
.
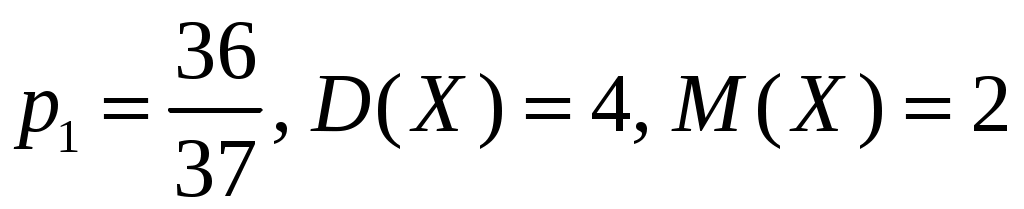 .
.Решение
Сумма вероятностей всех возможных значений дискретной случайной величины должна быть равна единице, поэтому вероятность
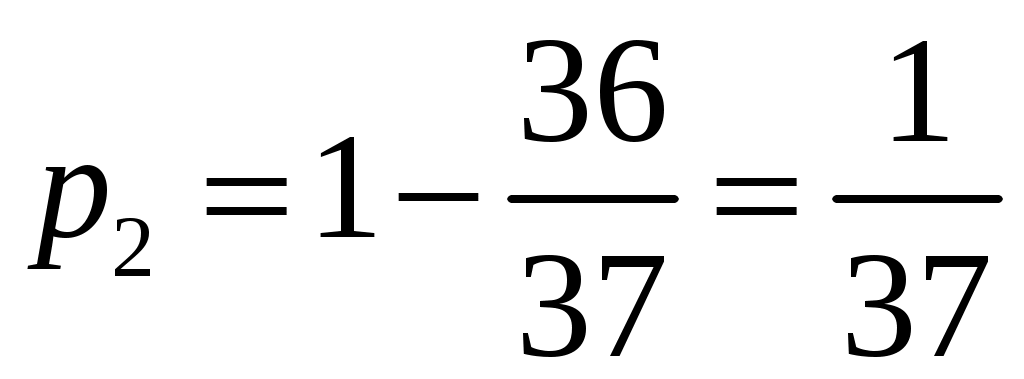 .
.Тогда закон распределения
По определению:
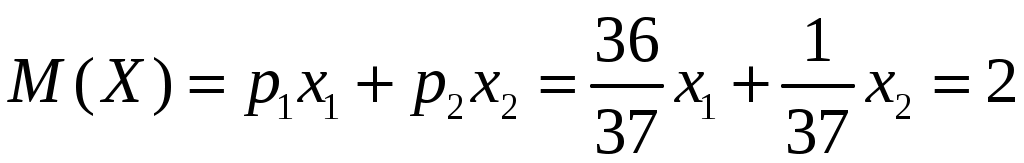 ;
;Напишем закон распределения
Найдём
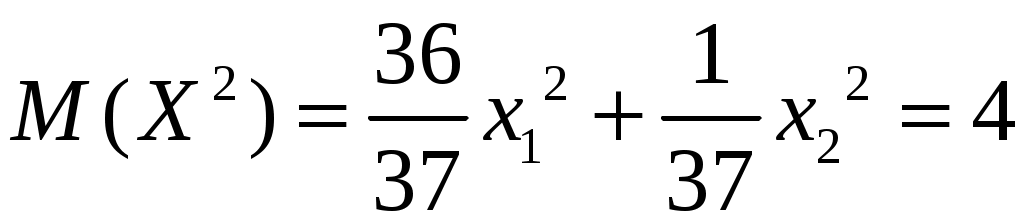 ,
,тогда
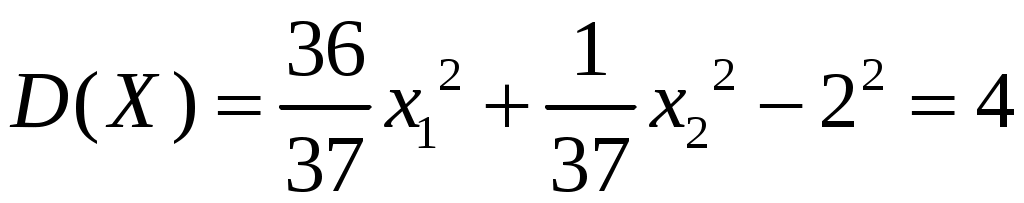 .
.Имеем систему уравнений для нахождения
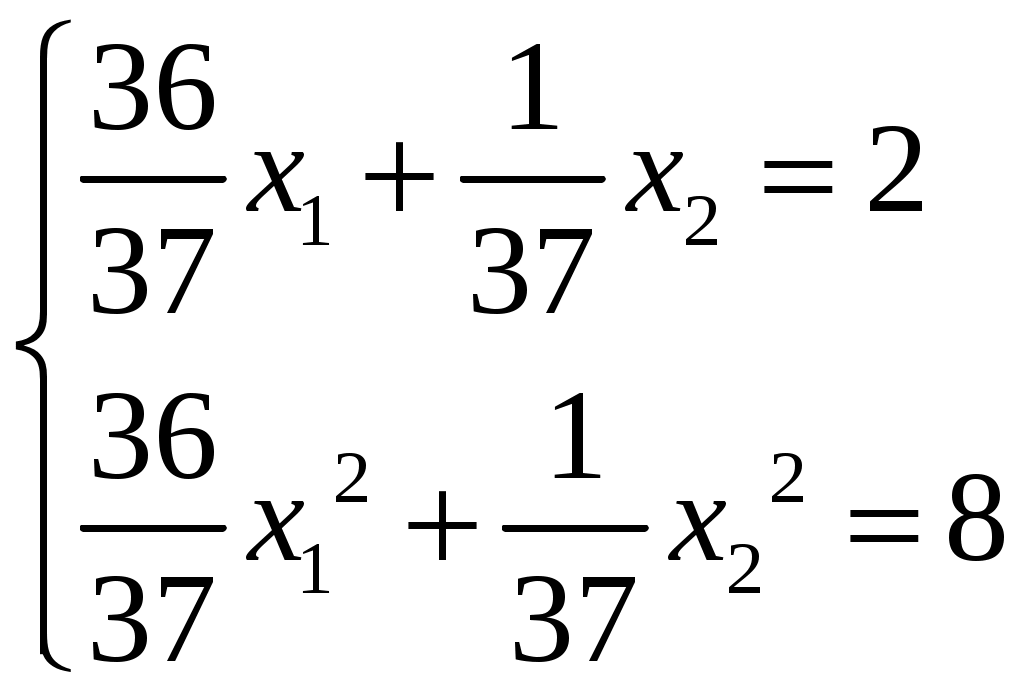 .
.Решая систему, найдём:
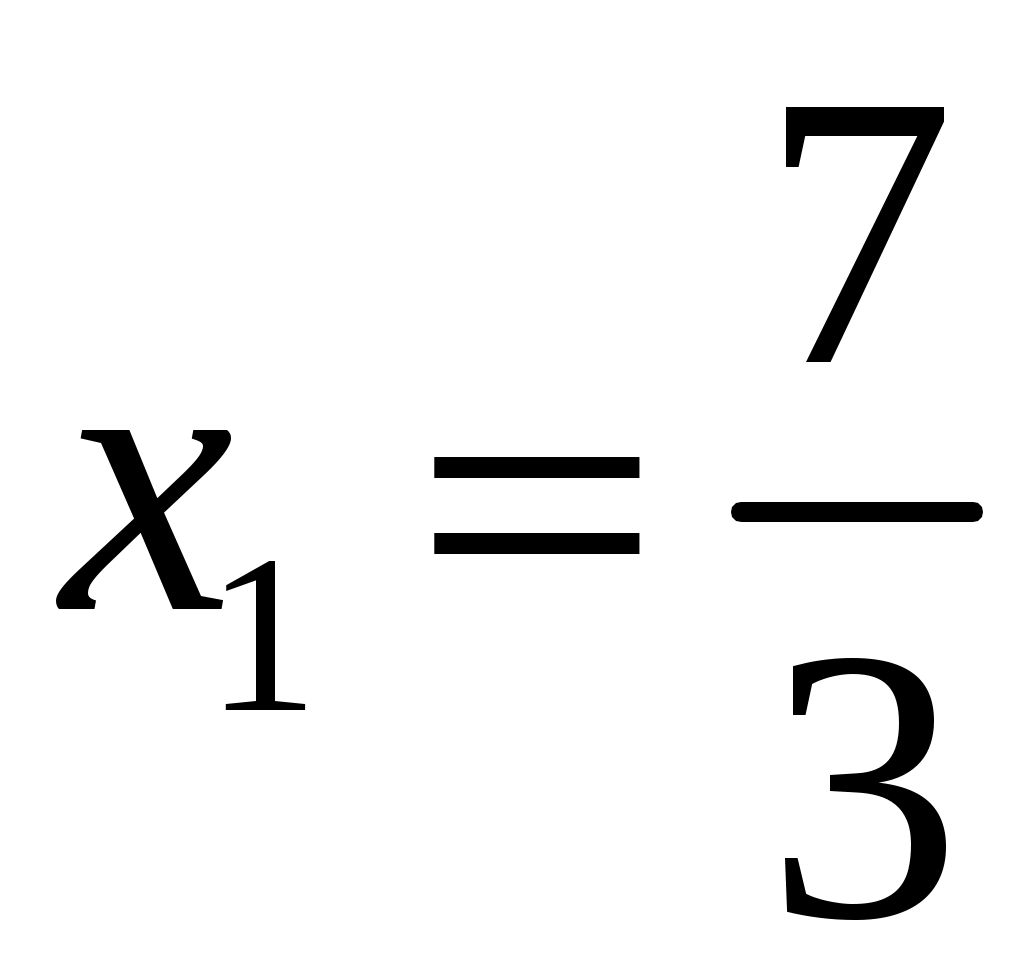 ,
, 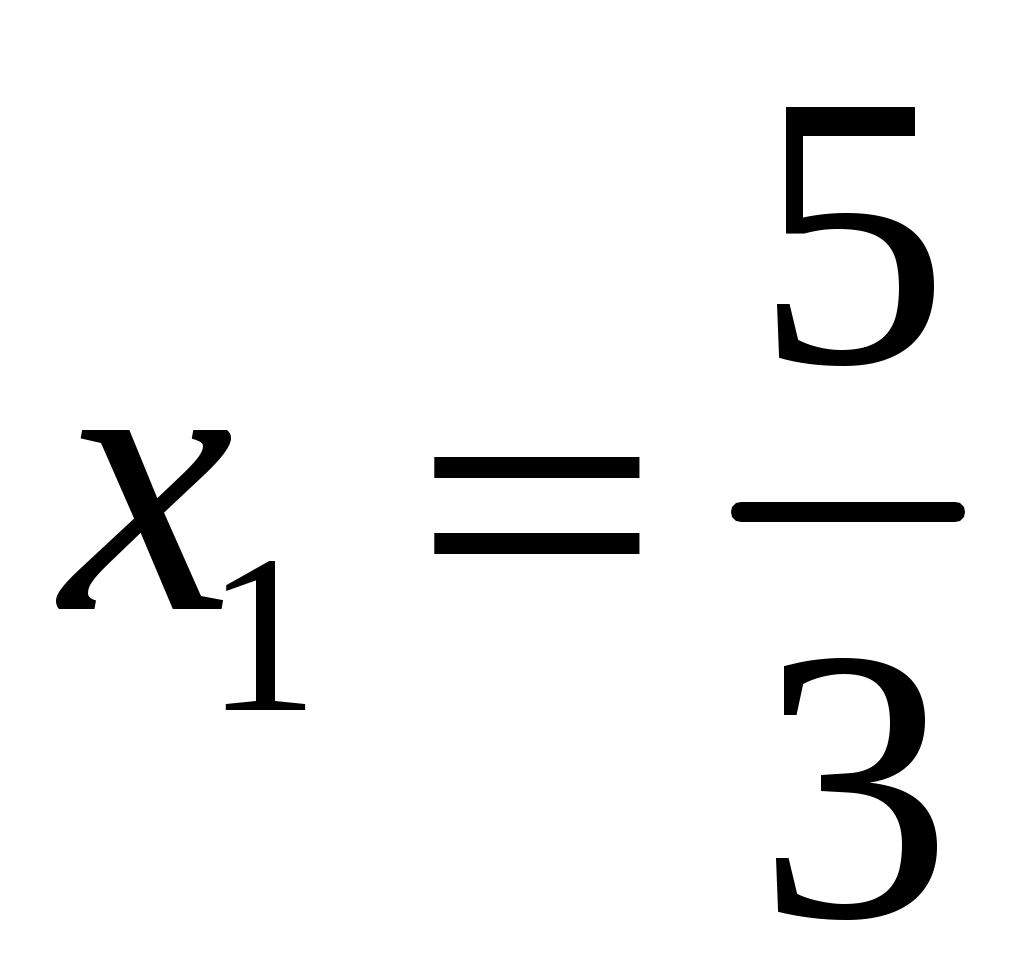 ,
, -

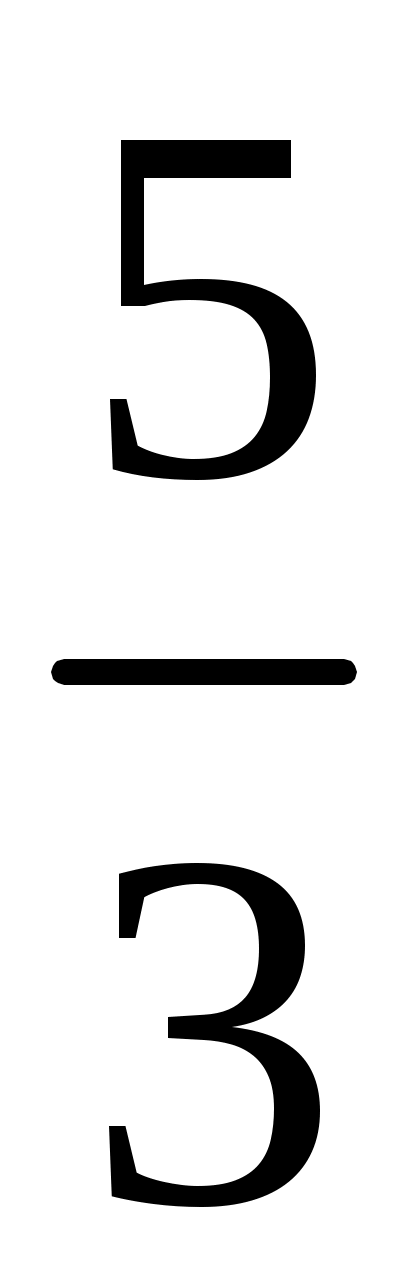
14



Задача №14
Случайная величина
1) найти плотность вероятности;
2) математическое ожидание и дисперсию
3) построить графики функции распределения и функции плотности распределения.
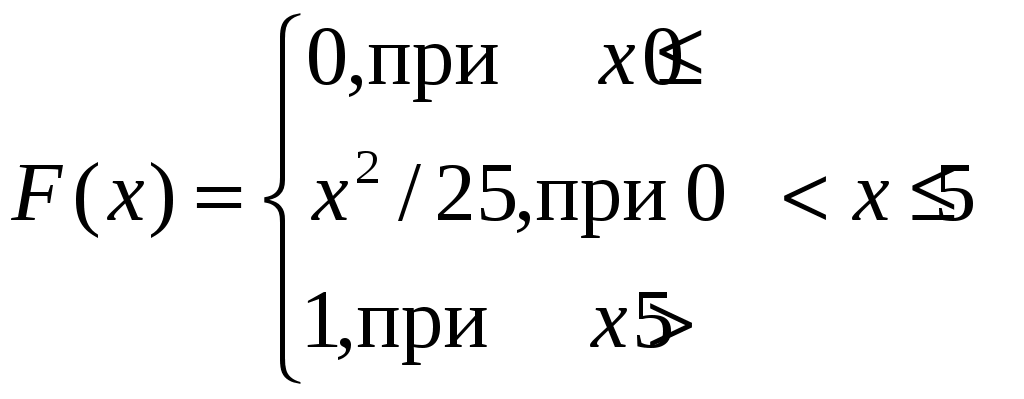 .
.Решение
Найдём плотность распределения. По определению:
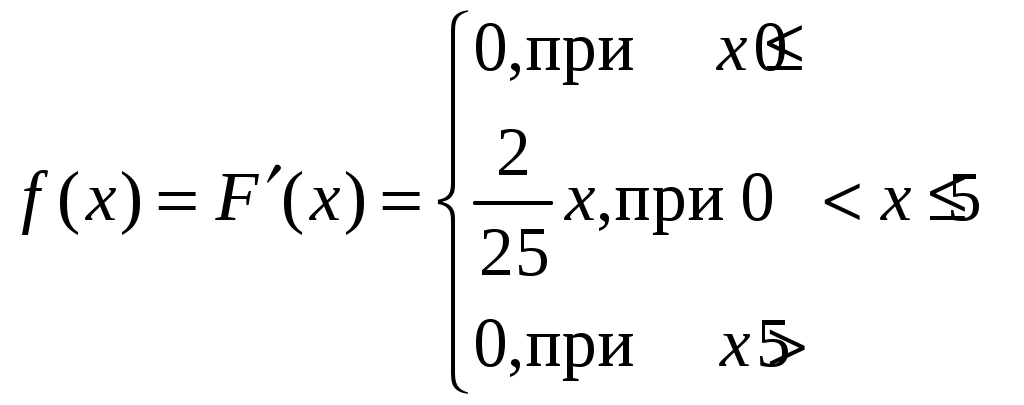 .
.Тогда
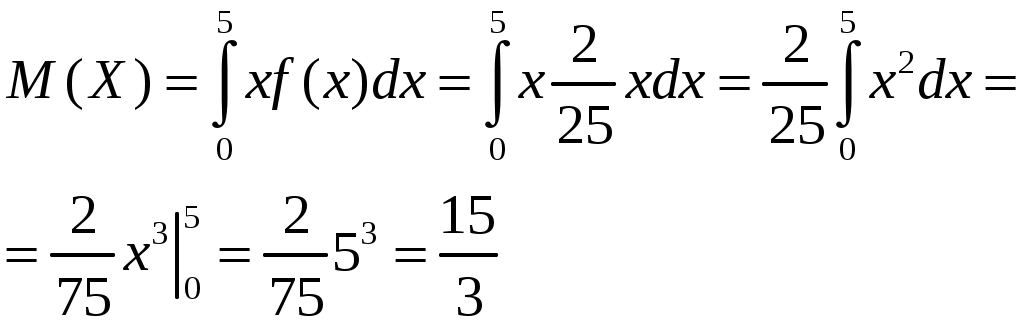 ,
,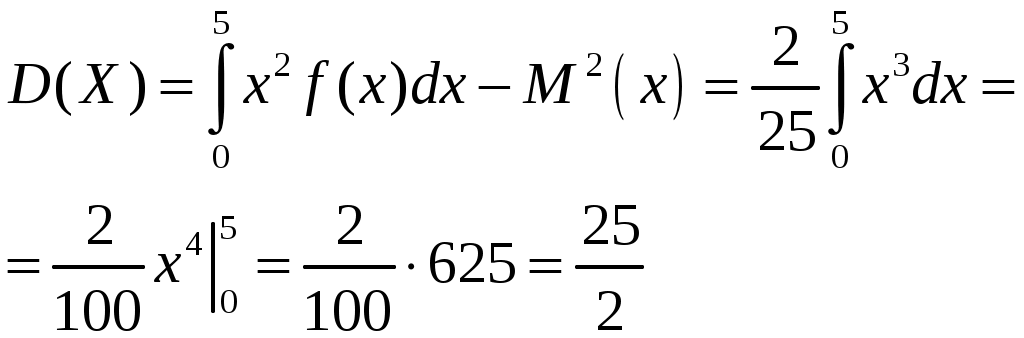 .
.График функции распределения представлен на рисунке а)

Рисунок а
График функции плотности распределения представлен на рисунке б).

Рисунок б
Задача №15
Заданы математическое ожидание
Решение
1) Воспользуемся формулой:
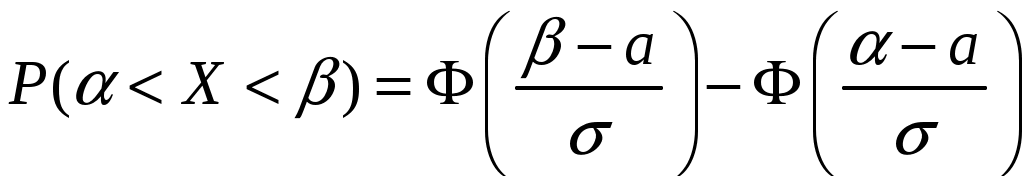 ,
,подставив
, получим:
По таблицам приложения находим
2) Искомая вероятность находится по формуле:
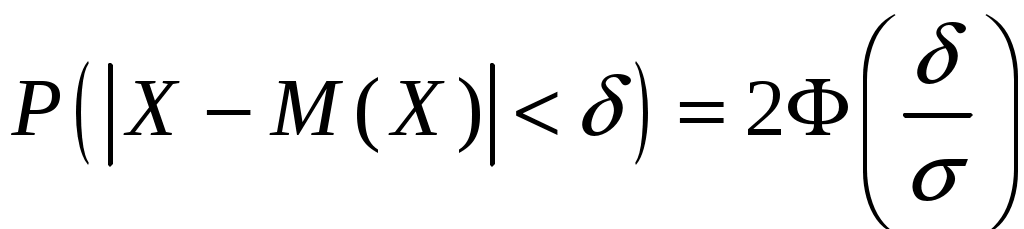 .
.По условию
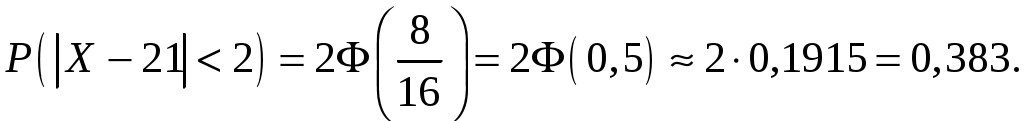
Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность
4) При уровне значимости
Выборка объёма
| 324 | 296 | 313 | 323 | 312 | 321 | 322 | 301 | 337 | 322 | 329 | 307 |
| 301 | 328 | 312 | 318 | 327 | 315 | 319 | 317 | 309 | 334 | 323 | 340 |
| 326 | 322 | 314 | 335 | 313 | 322 | 319 | 325 | 312 | 300 | 323 | 335 |
| 339 | 326 | 298 | 298 | 337 | 322 | 303 | 314 | 315 | 310 | 316 | 321 |
| 312 | 315 | 331 | 322 | 321 | 336 | 328 | 315 | 338 | 318 | 327 | 323 |
| 325 | 314 | 297 | 303 | 322 | 314 | 317 | 330 | 318 | 320 | 312 | 333 |
| 332 | 319 | 325 | 319 | 307 | 305 | 316 | 330 | 318 | 335 | 327 | 321 |
| 332 | 288 | 322 | 334 | 295 | 318 | 329 | 305 | 310 | 304 | 326 | 319 |
| 317 | 316 | 316 | 307 | 309 | 309 | 328 | 317 | 317 | 322 | 316 | 304 |
| 303 | 350 | 309 | 327 | 345 | 329 | 338 | 311 | 316 | 324 | 310 | 306 |
| 308 | 302 | 315 | 314 | 343 | 320 | 304 | 310 | 345 | 312 | 330 | 324 |
| 308 | 326 | 313 | 320 | 328 | 309 | 306 | 306 | 308 | 324 | 312 | 309 |
| 324 | 321 | 313 | 330 | 330 | 315 | 320 | 313 | 302 | 295 | 337 | 346 |
| 327 | 320 | 307 | 305 | 323 | 331 | 345 | 315 | 318 | 331 | 322 | 315 |
| 304 | 324 | 317 | 322 | 312 | 314 | 308 | 303 | 333 | 321 | 312 | 323 |
| 317 | 288 | 317 | 327 | 292 | 316 | 322 | 319 | 313 | 328 | 313 | 309 |
| 329 | 313 | 334 | 314 | 320 | 301 | 329 | 319 | 332 | 316 | 300 | 300 |
| 304 | 306 | 314 | 323 | 318 | 337 | 325 | 321 | 322 | 288 | 313 | 314 |
| 307 | 329 | 302 | 300 | 316 | 321 | 315 | 323 | 331 | 318 | 334 | 316 |
| 328 | 294 | 288 | 312 | 312 | 315 | 321 | 332 | 319 | | | |