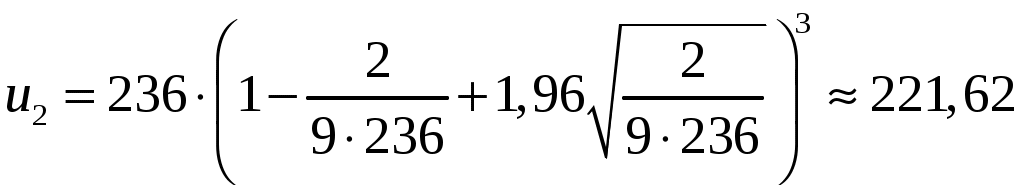Решение

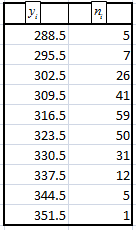
1. Упорядочив данные выборки по возрастанию, и найдя соответствующие частоты встречающихся значений, получим таблицу, задающую статистическое распределение выборки:


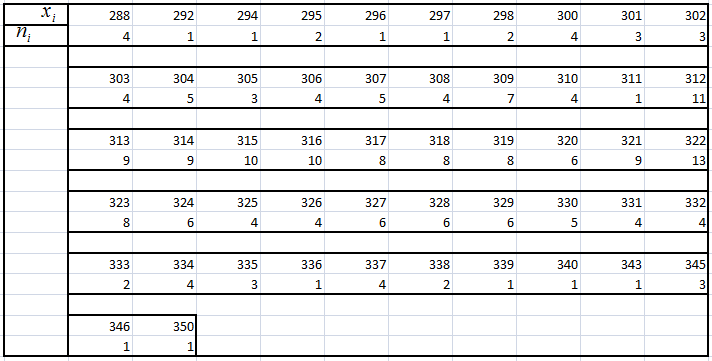
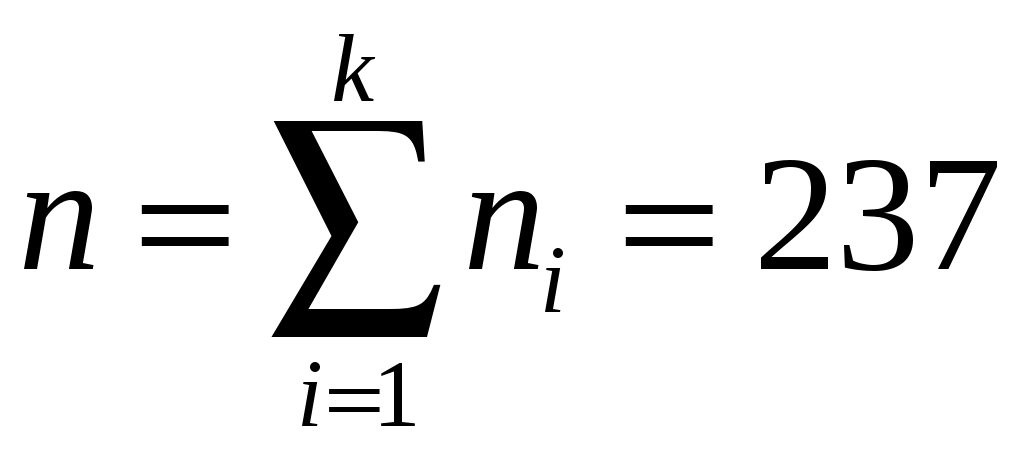 – объём выборки.

Разобьём интервал данных на 10 частичных интервала длины : 285 – 292; 292 – 299; 299 – 306; 306 – 313; 313 – 320; 320 – 327; 327 – 334; 334 – 341; 341 – 348; 348 – 355, и найдём новые частоты , приняв в качестве их значений сумму частот данных выборки, попавших в i-ый интервал. Итак:

; ; ; , ,

, ,

, ,

Вычислим плотности частот и построим таблицу распределения выборки для построения гистограммы частот:

	5	7	26	41
	0,021	0,03	0,11	0,173

---

59	50	31	12	5
0,249	0,211	0,131	0,051	0,021

1

0,004

Гистограмма частот изображена на рисунке:



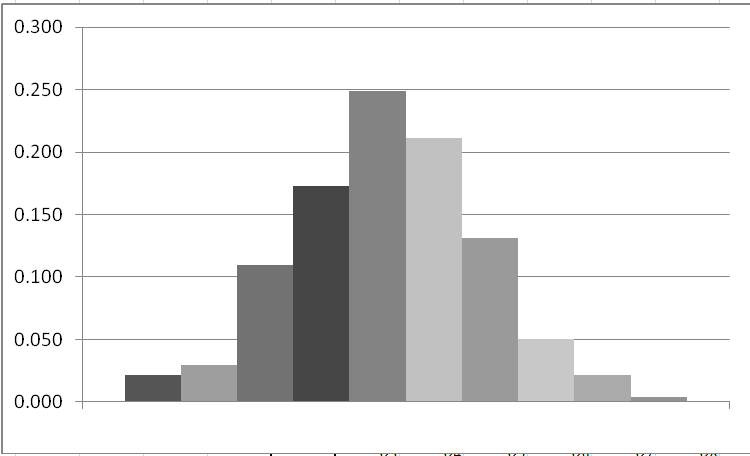
Рисунок

2. Приняв в качестве новых вариант серединные значения частичных интервалов , построим распределение равноотстоящих вариант для вычисления точечных оценок генеральной средней и дисперсии методом произведений.



Напомним процедуру вычисления оценок генеральной средней и дисперсии по методу произведений.

Выберем .

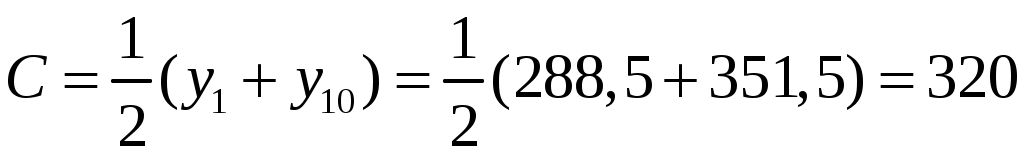Вычислим  – условные варианты.

Найдём  – условный момент первого порядка,

 – условный момент второго порядка.

---

Тогда:

 – выборочная средняя,

 – выборочная дисперсия.

Результаты вычислений сведём в таблицу:



; ;

;

.

.

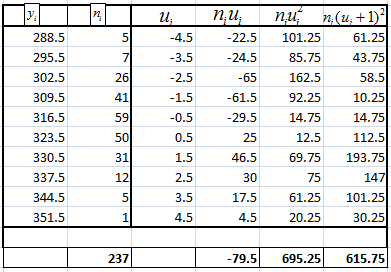
3. Для получения интервальной оценки математического ожидания нормально распределённой случайной величины по выборочной средней и неизвестной дисперсии используем формулу:

,

где  – «исправленное» выборочное средне квадратическое отклонение,  – случайная величина распределённая по закону Стьюдента с числом степеней свободы (находится по таблице при заданных и ).

Найдём .

Имеем .

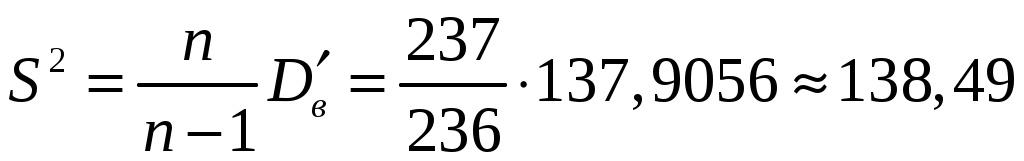Отсюда . При и имеем и

---

. Тогда доверительный интервал для математического ожидания равен:

.

Для получения интервальной оценки дисперсии нормальной генеральной совокупности используют случайную величину 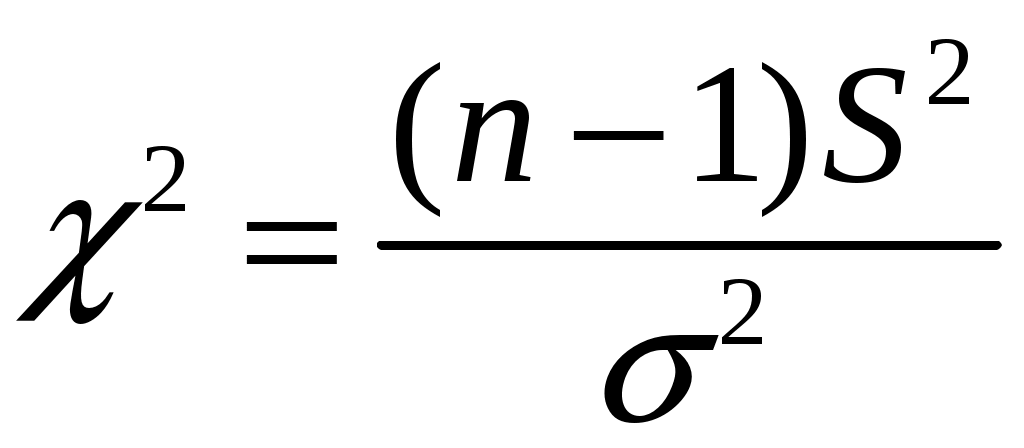. Величина имеет распределение Пирсона с числом степеней свободы и представлена в таблицах. По этим таблицам определяются два числа (критические точки распределения ) и :

, ;

, .

---

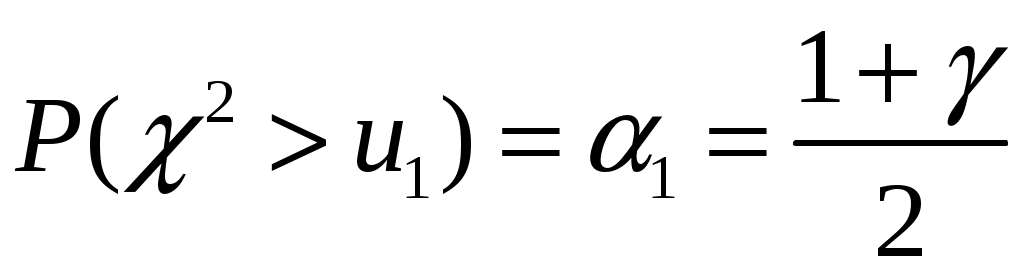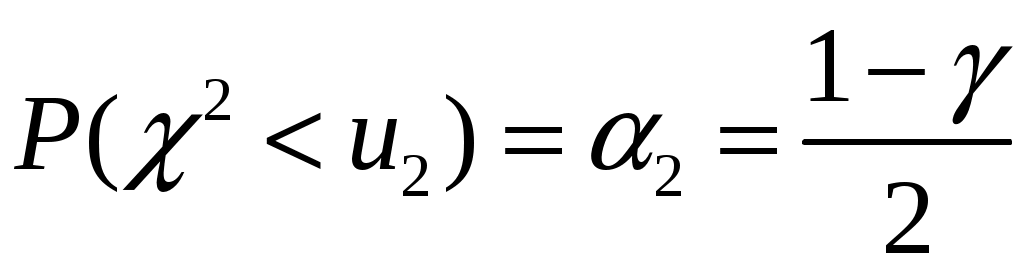Замечание Если число степеней свободы , то критическую точку можно найти из равенства Уилсона-Гильферти:

,

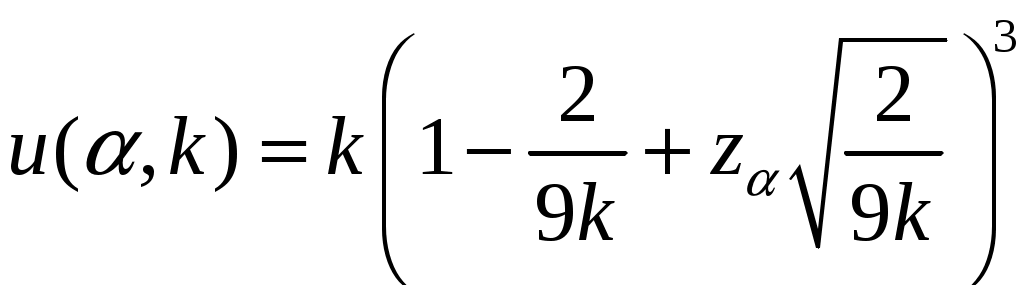где находят из равенства , используя функцию Лапласа.

Тогда доверительный интервал для дисперсии можно записать в виде:

.

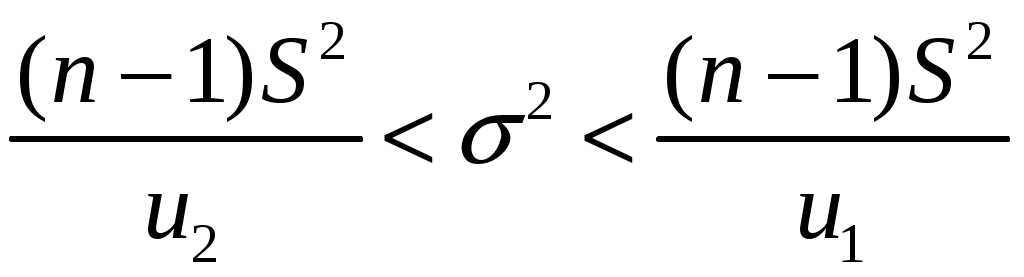В нашей задаче по условию . Тогда, ; ; .

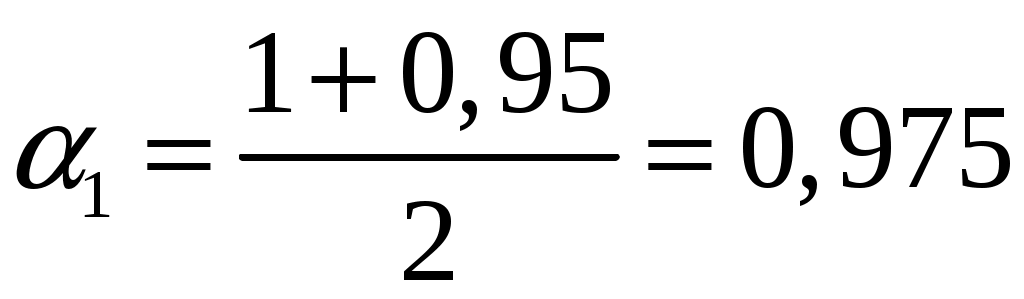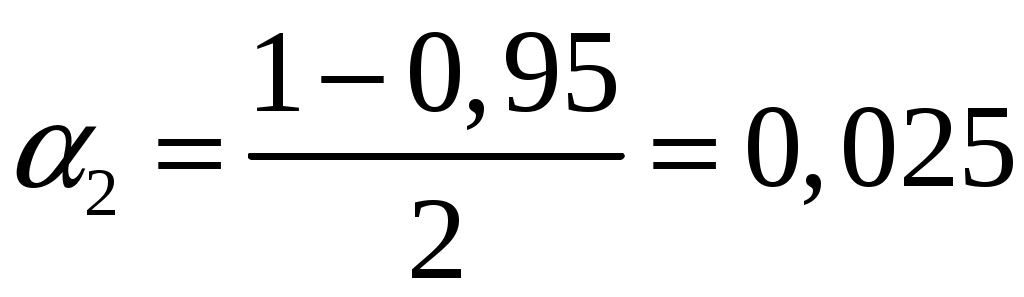Так как в нашем случае используем равенство Уилсона-Гильферти для нахождения и :

; ;

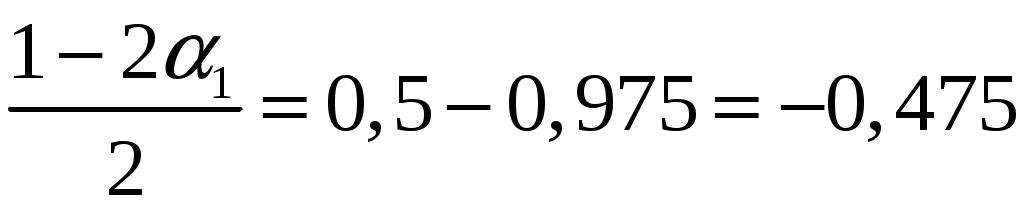из равенства находим . Тогда:

.

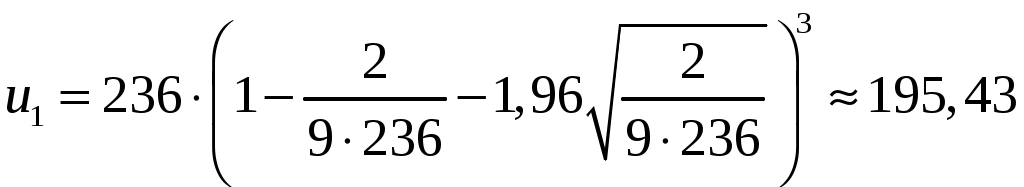Аналогично:

; ;

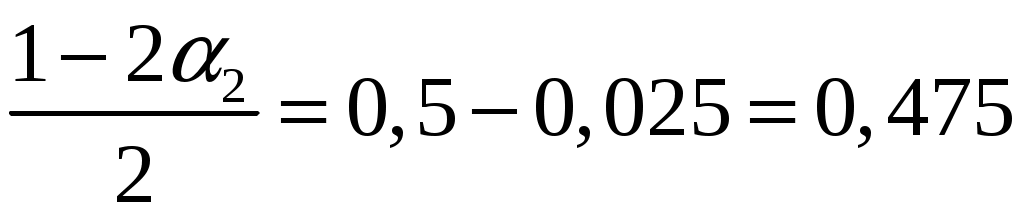из равенства находим . Тогда:

---

Смотрите также файлы

• Сюжет произведения.docx

• ысамерзімді жоспар Сабаты таырыбы Энергия трлері мен кздері.docx

• Акушерия ынапты жуу,булау.docx

• Великая французская революция.docx

• В конце 20 века Россия перешла к рыночной экономике.docx