Файл: Задача 1 Вычислить двойной интеграл от функции по заданной области . Решение Вид области представлен на рисунке.doc
Добавлен: 29.11.2023
Просмотров: 73
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
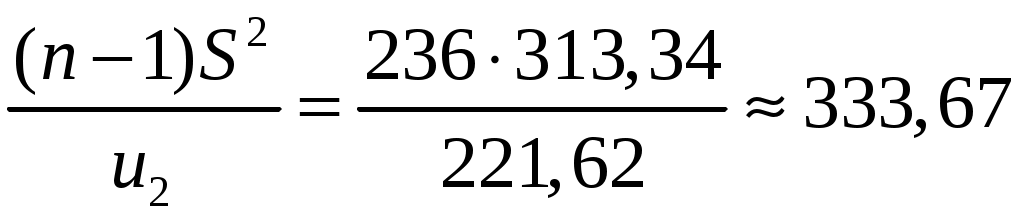 ;
; 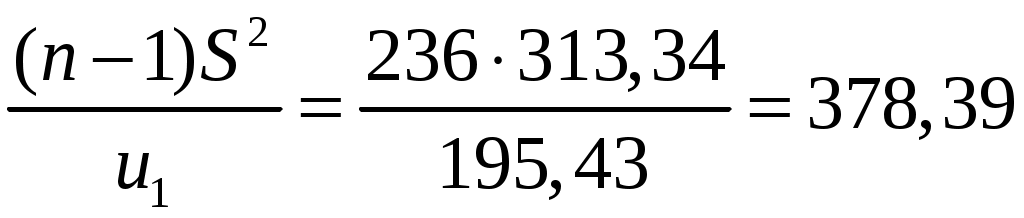 .
.
Таким образом, доверительный интервал для дисперсии:
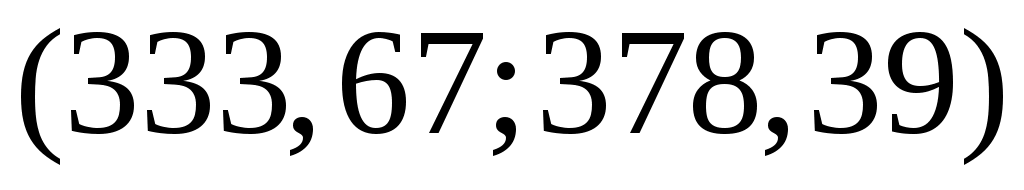 .
.
4. Считаем, что эмпирическое распределение задано в виде последовательности интервалов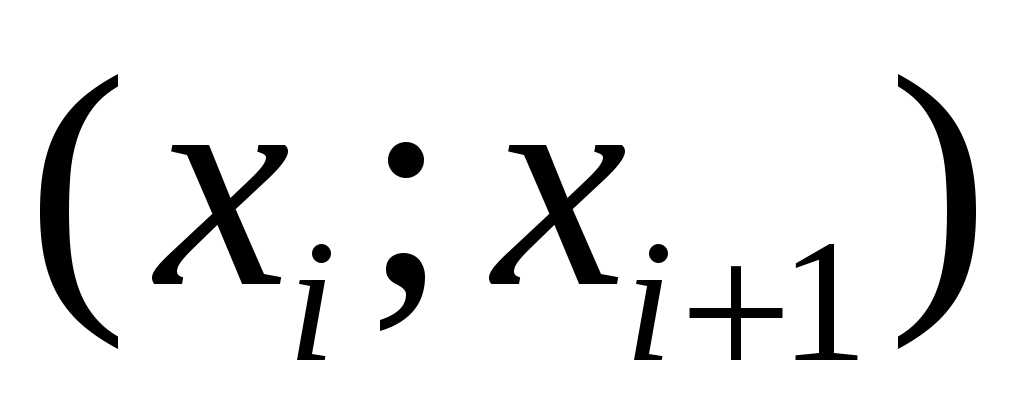 и соответствующих им частот:
и соответствующих им частот:
Перейдём к новой случайной величине: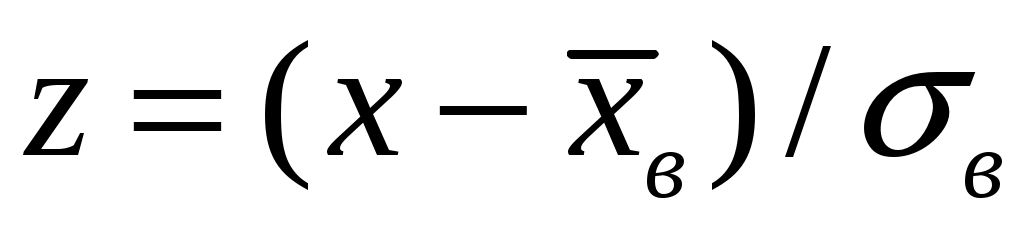 и вычислим концы интервалов
и вычислим концы интервалов 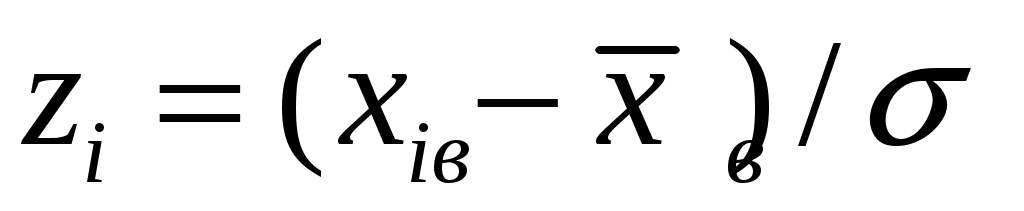 , полагая
, полагая 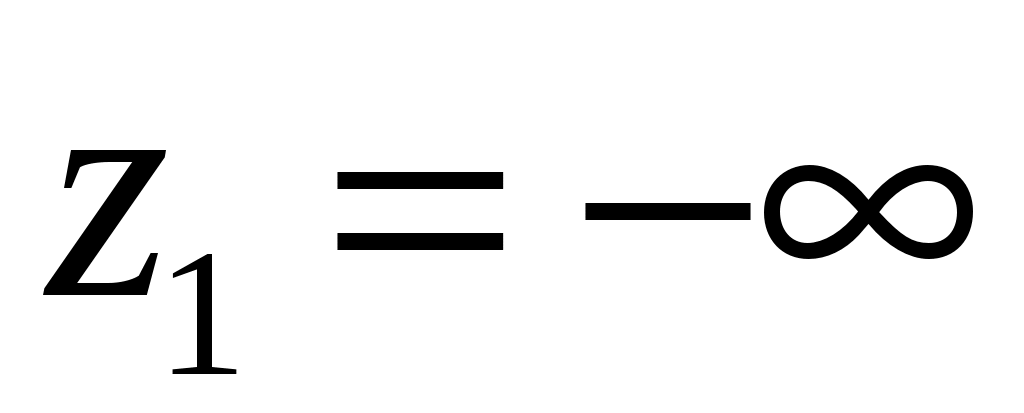 ,
, 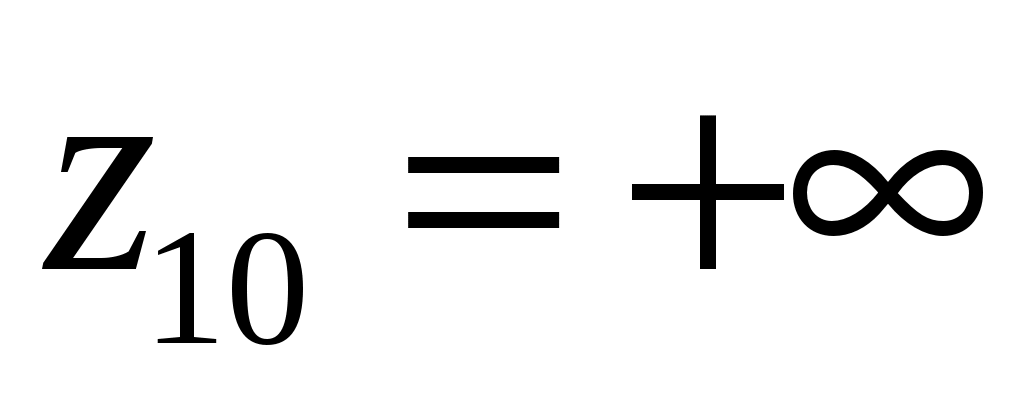 ,
, 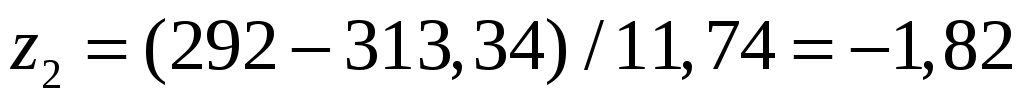 ;
; 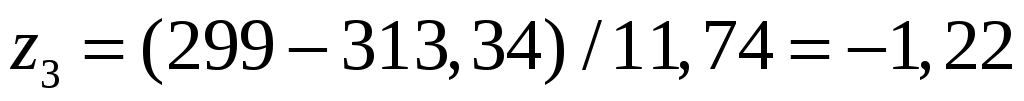 ;
; 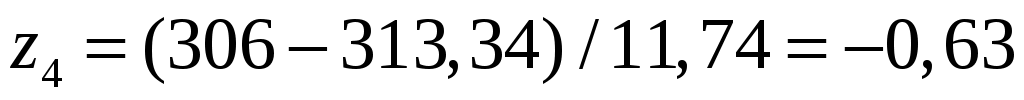 ,
,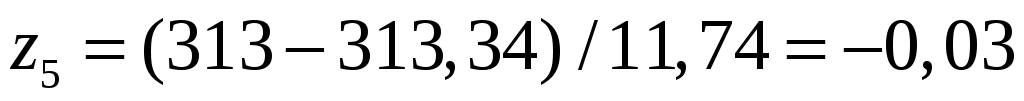 ,
,
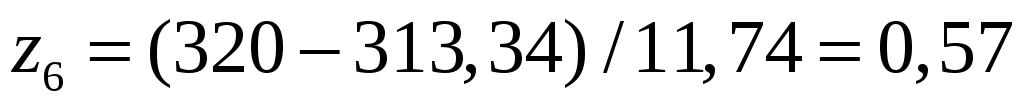 ,
,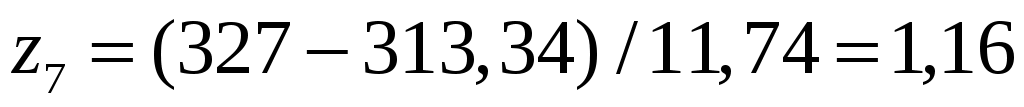 ,
,
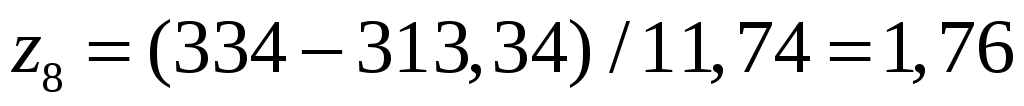 ,
,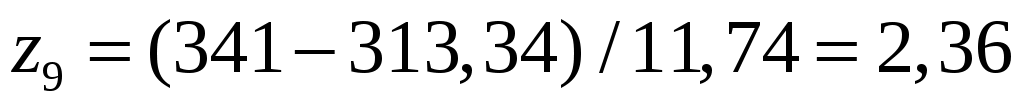 ,
,
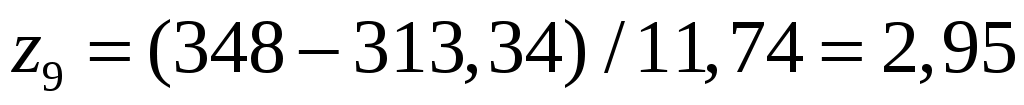
Найдём теоретические вероятности попадания случайной величины в интервал
в интервал 
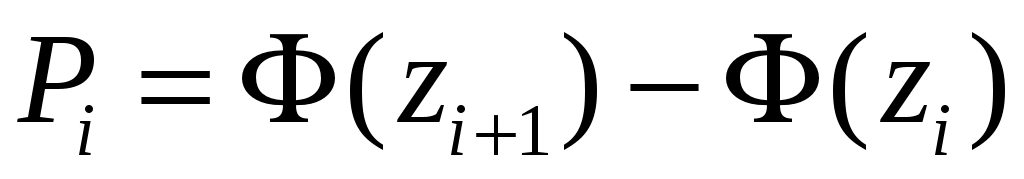 , здесь
, здесь 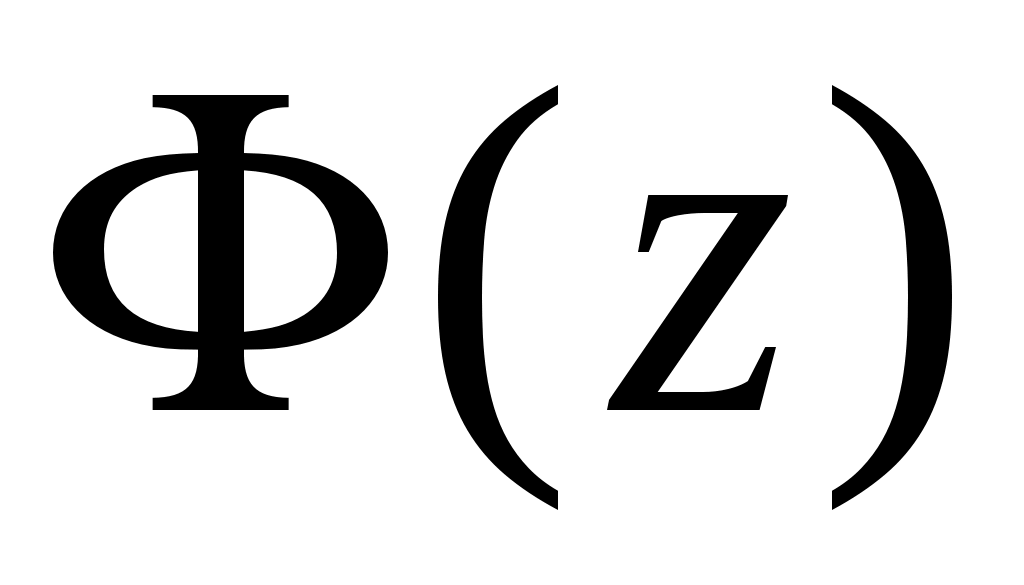 – функция Лапласа.
– функция Лапласа.
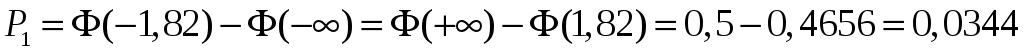 ;
;
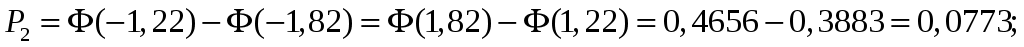
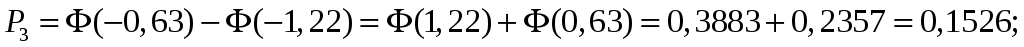
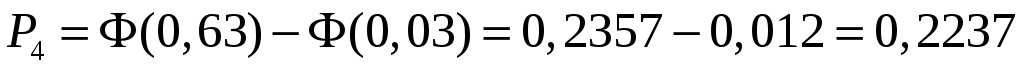 .
.
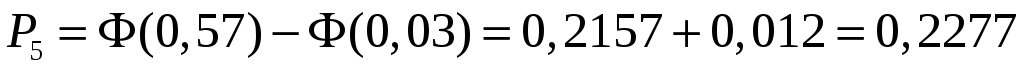
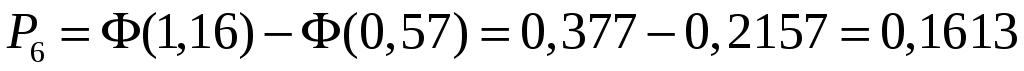
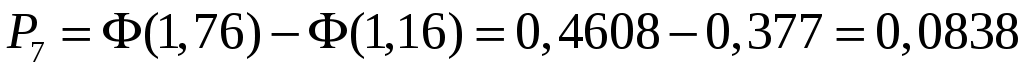
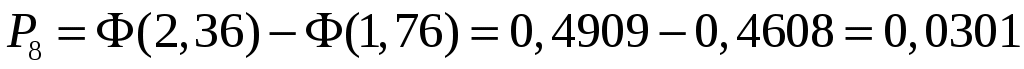
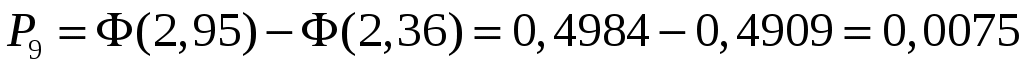
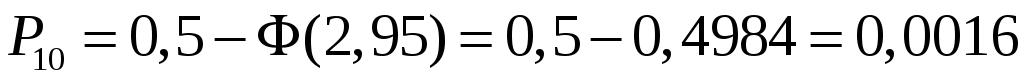
Проверка: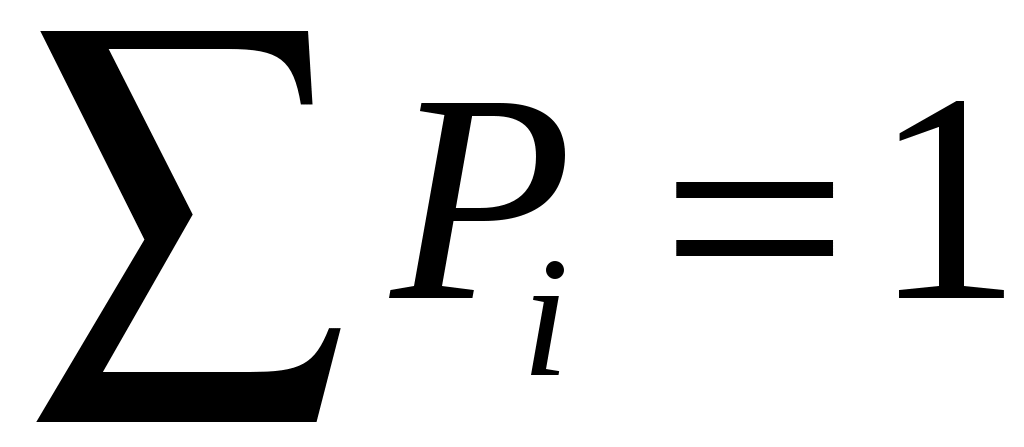 .
.
Вычислим теоретические частоты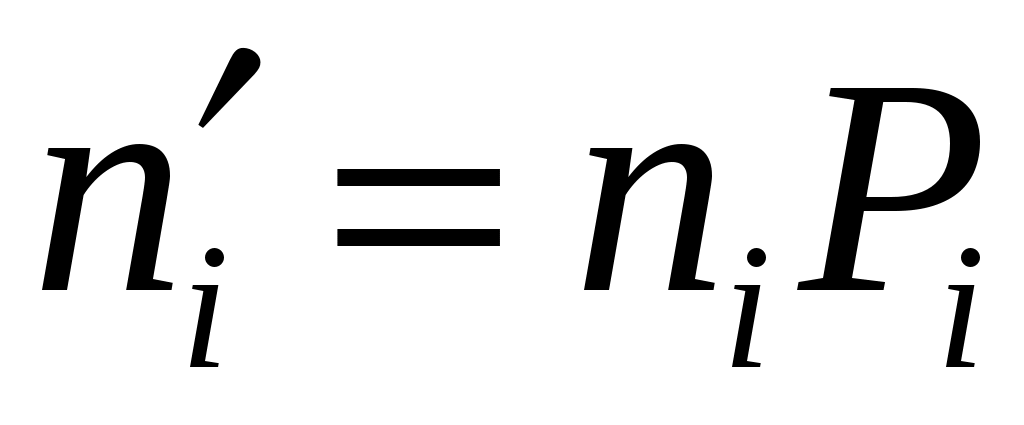 :
:
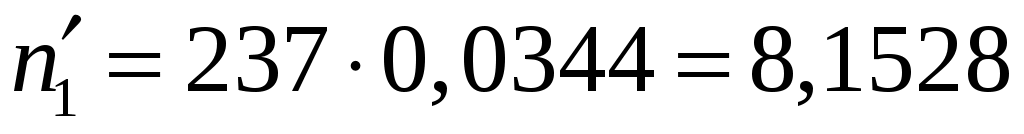 ;
; 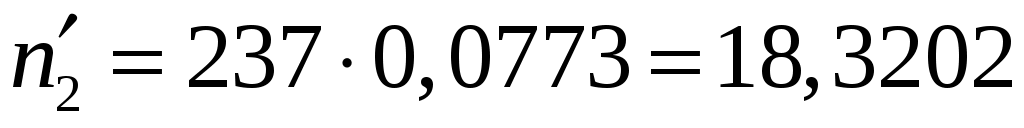 ;
;
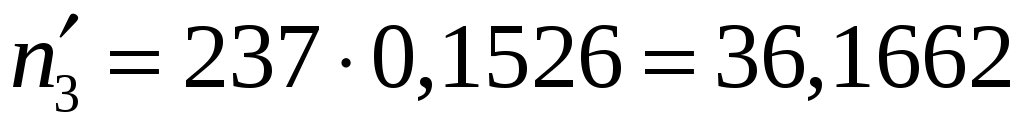 ;
; 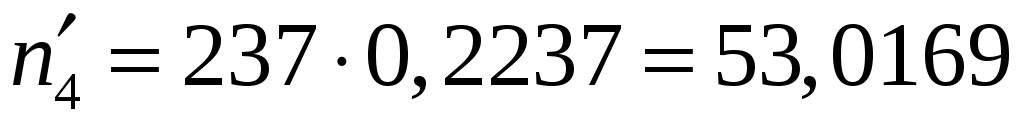 ,
,
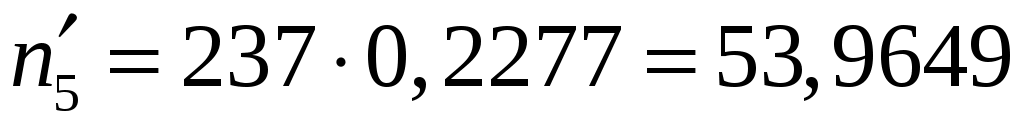 ,
,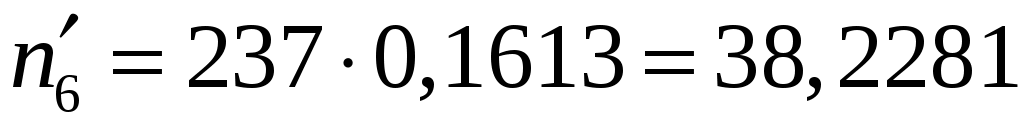 ,
,
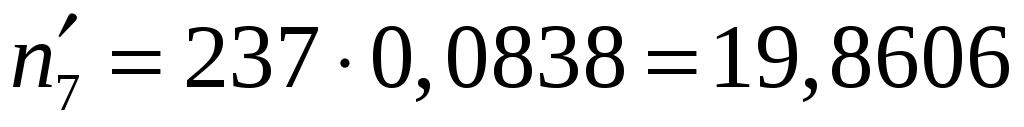 ,
,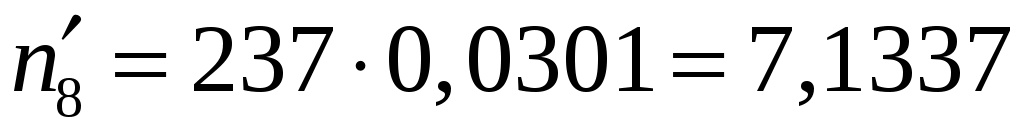 ,
,
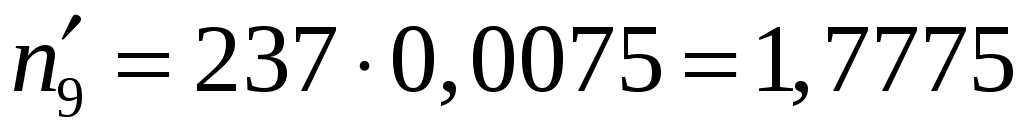 ,
,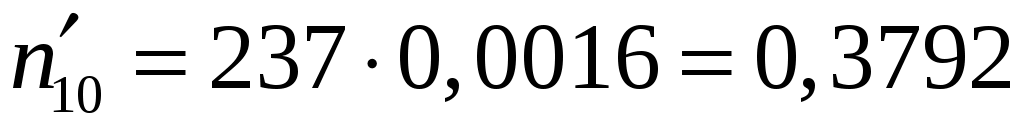 .
.
Найдём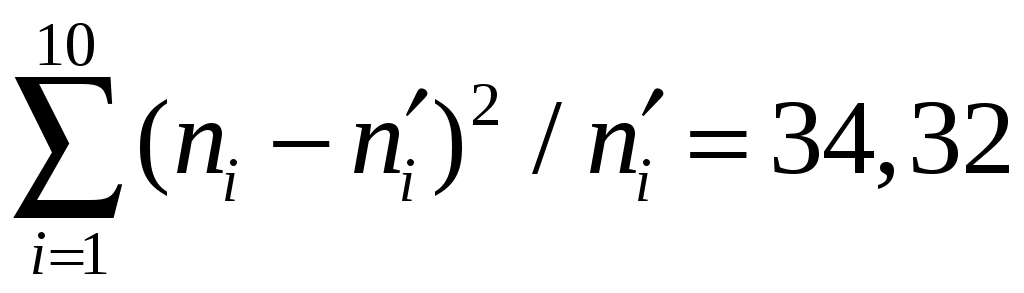
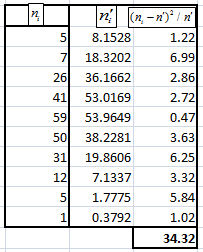
.
По таблице критических точек распределения , по заданному уровню значимости
, по заданному уровню значимости 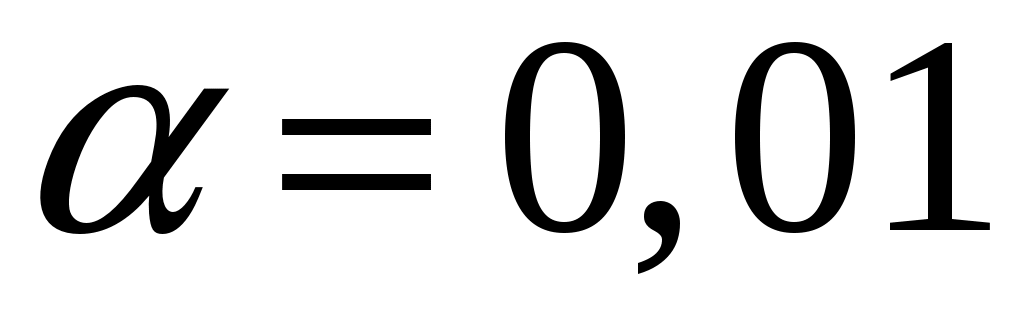 и числу степеней свободы
и числу степеней свободы 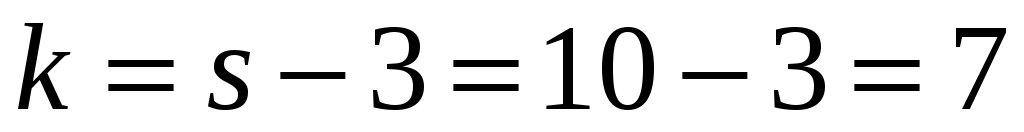 , (где
, (где 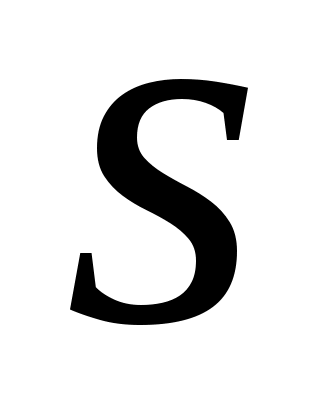 – число интервалов выборки) находим критическую точку правосторонней критической области:
– число интервалов выборки) находим критическую точку правосторонней критической области: 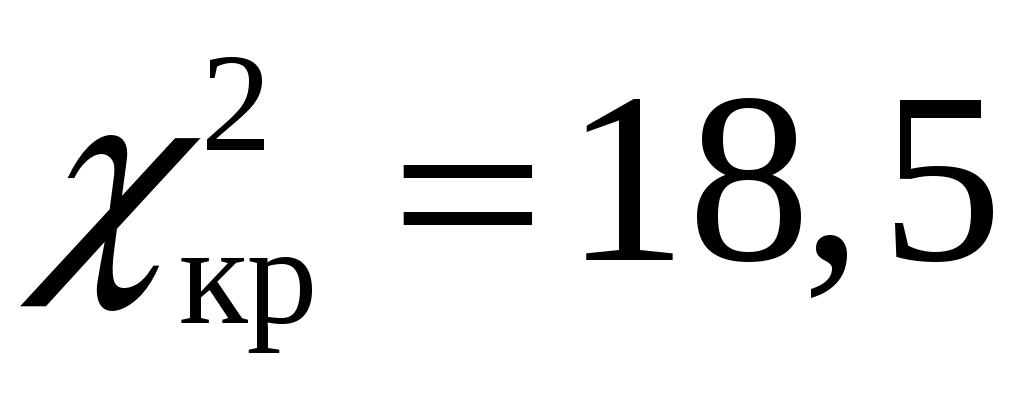 . Так как
. Так как 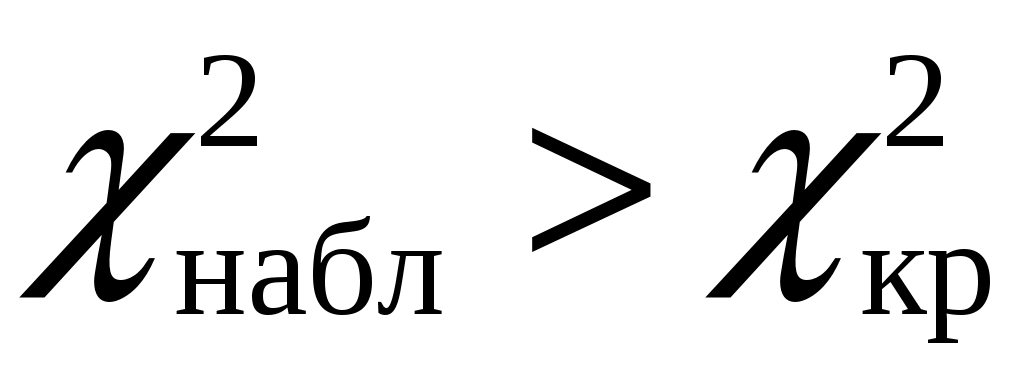 , то гипотезу о нормальном распределении генеральной совокупности отвергаем.
, то гипотезу о нормальном распределении генеральной совокупности отвергаем.
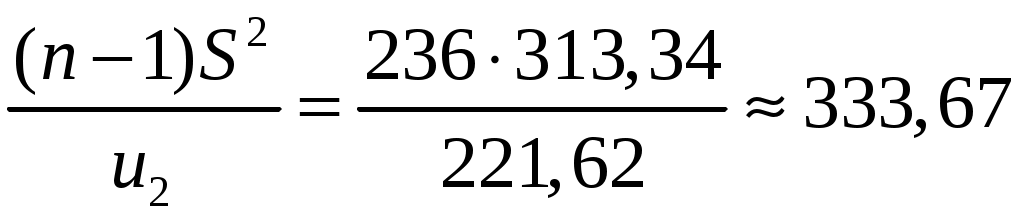 ;
; 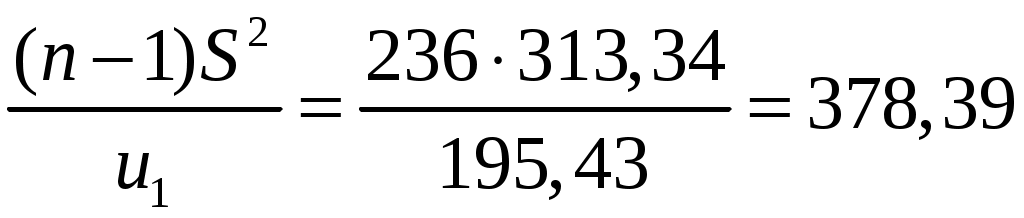 .
.Таким образом, доверительный интервал для дисперсии:
4. Считаем, что эмпирическое распределение задано в виде последовательности интервалов
| | | | | |
| | 5 | 7 | 26 | 41 |
| | | | | |
| | | | | |
| 59 | 50 | 31 | 12 | 5 |
| | | | | |
| |
| 1 |
| |
Перейдём к новой случайной величине:
Найдём теоретические вероятности попадания случайной величины
Проверка:
Вычислим теоретические частоты
Найдём
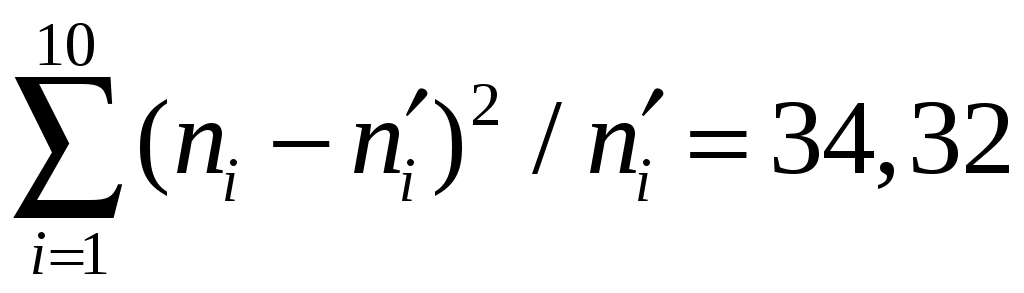

.
По таблице критических точек распределения