Файл: Семинар сынылады he жне spo жйесіндегі омо сарапшылы кеесі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 605
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
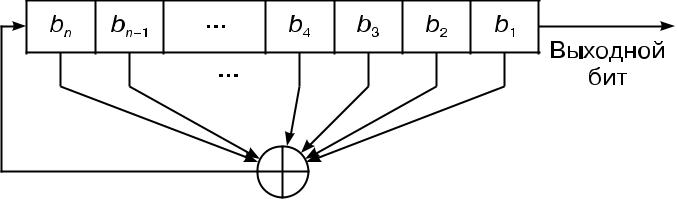
Күріш. 3.9.RgSsLOS Fibbonachi
-
Жалпы алғанда, n-разрядты PrCsLOS бірінде болуы мүмкін
бастап N = 2n– 1 ішкі күй. Бұл теориялық тұрғыдан мұндай регистр псевдокездейсоқ тізбекті құра алады дегенді білдіреді
периоды Т = 2 болатын несn– 1 бит. (Ішкі күйлердің саны және период N = Tмакс= 2n– 1, өйткені PrCsLOS-ті нөлдермен толтыру ауысым регистрінің нөлдердің шексіз тізбегін шығаруына әкеледі, бұл мүлдем пайдасыз.) Тек PrCsLOS-тың белгілі бір реттік түрту ретімен циклдік түрде
2-нің барлығынан өтедіn– 1 ішкі күй, мұндай RgSsLOS – максималды кезеңі бар RgSsLOS. Алынған нәтиже М-тізбегі деп аталады.
Мысал.3.10-суретте бірінші және төртінші биттерден алынған төрт разрядты PgCsLOS көрсетілген. Егер ол 1111 мәнімен инициализацияланса, онда қайталау алдында регистр келесі ішкі күйлерді қабылдайды (3.4-кесте).
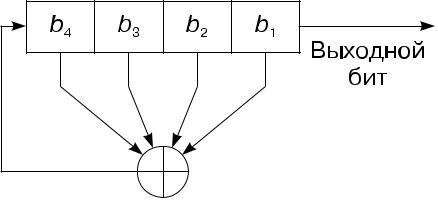
Күріш. 3.10.Бірінші және төртінші биттерден түрту арқылы төрт разрядты PrCsLOS
1223-БӨЛІМ

| | | | | | | 3.4-кесте | | ||
| | | | | | | | | | |
| | Жолақ нөмірін жылжыту | Тіркелу күйі | шығыс биті | | |||||
| | (ішкі күй) | Т1 | Т2 | Т3 | Т4 | | |||
| | | | | ||||||
| Бастапқы мән | 1 | 1 | 1 | 1 | — | | |||
| 1 | | 0 | 1 | 1 | 1 | 1 | | | |
| 2 | | 1 | 0 | 1 | 1 | 1 | | | |
| 3 | | 0 | 1 | 0 | 1 | 1 | | | |
| 4 | | 1 | 0 | 1 | 0 | 0 | | | |
| 5 | | 1 | 1 | 0 | 1 | 1 | | | |
| 6 | | 0 | 1 | 1 | 0 | 0 | | | |
| 7 | | 0 | 0 | 1 | 1 | 1 | | | |
| 8 | | 1 | 0 | 0 | 1 | 1 | | | |
| 9 | | 0 | 1 | 0 | 0 | 0 | | | |
| 10 | | 0 | 0 | 1 | 0 | 0 | | | |
| он бір | | 0 | 0 | 0 | 1 | 1 | | | |
| 12 | | 1 | 0 | 0 | 0 | 0 | | | |
| 13 | | 1 | 1 | 0 | 0 | 0 | | | |
| 14 | | 1 | 1 | 1 | 0 | 0 | | | |
| 15 | (бастапқы күйге оралу) | 1 | 1 | 1 | 1 | 1 | | | |
| 16 | (күйлерді қайталау) | 0 | 1 | 1 | 1 | 1 | | | |
Шығару тізбегі ең аз мәнді биттердің жолы болады: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 кезеңімен T = 15, мүмкін болатын ішкі күйлердің жалпы саны (нөлден басқа) N = 24– 1 = 16 – 1 = 15 = Тмакс, демек, шығыс тізбегі M-тізбегі болып табылады.
Белгілі бір RgCsLOS максималды периодқа ие болуы үшін түрткі тізбегінен құрылған көпмүше және 1 тұрақтысы қарабайыр модуль 2 болуы керек. Көпмүше градустардың қосындысы ретінде көрсетіледі, мысалы, n дәрежелі көпмүшелік ретінде көрсетіледі. мынадай:
аnxn+ аn–1xn–1+ … + a1x1+ а0x0= аnxn+ аn–1xn–1+ … + a1x+ а0,
қайда амен= {0,1} i = 1 … n үшін, балтамен- дәрежесін көрсетеді.
Көпмүшенің дәрежесі - жылжу регистрінің ұзындығы. n дәрежелі қарабайыр көпмүше х-тің бөлгіші болатын азайтылмайтын көпмүше.2n–1+ 1, бірақ х-тің бөлгіші емесг2-нің барлық d бөлгіштері үшін + 1n- 1.
-
Жалпы алғанда, модуль 2 берілген дәрежедегі қарабайыр көпмүшелерді құрудың оңай жолы жоқ. Ең оңай жолы –
Зертхана №12123

көпмүшені кездейсоқ түрде алып, оның қарабайыр екенін тексеріңіз. Бұл оңай емес және кездейсоқ таңдалған санның жай екенін тексеру сияқты, бірақ көптеген математикалық бағдарламалық қамтамасыз ету пакеттері мұны істей алады.
Кейбір, бірақ барлығы емес, әртүрлі дәрежедегі көпмүшелер, қарабайыр модуль 2, төменде келтірілген. Мысалы, белгілеу (32, 7, 5, 3, 2, 1, 0) келесі көпмүшенің 2-модульдің қарабайыр екенін білдіреді: x32+ x7+ x5+ x3+ x2+ x + 1.
Мұны PgCsLOS үшін максималды кезеңмен оңай жалпылауға болады. Бірінші сан PrCsLOS ұзындығы. Соңғы сан әрқашан 0 болады және оны өткізіп жіберуге болады. 0-ден басқа барлық сандар ауысым регистрінің сол жақ шетінен есептелетін түрту ретін көрсетеді. Басқаша айтқанда, төмен дәрежелі көпмүшенің мүшелері регистрдің оң жақ шетіне жақынырақ позицияларға сәйкес келеді.
Мысалды жалғастыра отырып, жазу (32, 7, 5, 3, 2, 1, 0) берілген 32 биттік ауысым регистрі үшін отыз екінші, жетінші, бесінші, үшінші, екінші XOR арқылы жаңа бит жасалатынын білдіреді.
-
бірінші биттің нәтижесінде алынған PrCsLOS максималды ұзындыққа ие болады, қайталамас бұрын 2-ден өтеді.32– 1 мән.
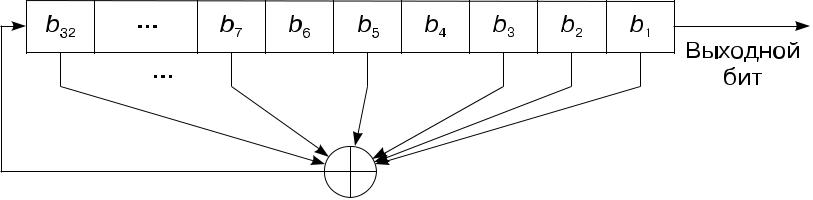
Күріш. 3.11.
Максималды ұзындығы бар 32 биттік PrCsLOS
PgCsLOS программалық кодын қарастырайық, онда түрту тізбегі полиноммен (32, 7, 5, 3, 2, 1, 0) сипатталады. Си тілінде ол келесідей көрінеді:
int LFSR()
{
статикалық қолтаңбасыз ұзын ShiftRegister = 1; /* 0-ден басқа кез келген нәрсе. */
ShiftRegister = ((((ShiftRegister >> 31)
^(ShiftRegister >> 6)
^(ShiftRegister >> 4)
^(ShiftRegister >> 2)
^(ShiftRegister >> 1)
1243-БӨЛІМ

^ShiftRegister))
&0x00000001)
<<31)
|(ShiftRegister >> 1);
ShiftRegister & 0x00000001 қайтару;
}
Ауысым регистрі компьютер сөзінен ұзағырақ болса, код күрделене түседі, бірақ көп емес. В қосымшасында кейбір қарабайыр көпмүшелердің кестесі 2 модуль бар, біз оны болашақта осы көпмүшелердің кейбір қасиеттерін анықтау үшін пайдаланамыз, сонымен қатар
-
түрту ретін орнатуға арналған бағдарламалық құралды іске асыру. Кестенің барлық элементтерінің тақ болатынын атап өткен жөн
коэффициенттер саны. Мұндай ұзын кесте PgCsLOS-пен әрі қарай жұмыс істеу үшін берілген, өйткені PgCsLOS көбінесе ағындық шифрлармен жұмыс істеу үшін және жалған кездейсоқ сандар генераторларында қолданылады.
-
Біздің жағдайда біз жетіден аспайтын ең жоғары дәрежелі көпмүшелерді пайдалана аламыз.
Егер p(x) қарабайыр болса, онда хnб(1 / x), сондықтан кестенің әрбір элементі шын мәнінде екі қарабайыр көпмүшені анықтайды. Мысалы, егер (a, b, 0) қарабайыр болса, онда (a, ab, 0). Егер (a, b, c, d, 0) қарабайыр болса, онда (a, ad, ac, ab, 0). Математикалық:
егер x қарабайыр болсаа+ xб+ 1, онда ол қарабайыр және ха+ xаб+ 1, егер x қарабайыр болсаа+ xб+ xв+ xг+ 1, онда ол қарабайыр және ха+ xжарнама+ xак+ xаб+ 1.
Қарапайым үш мүшелер бағдарламалы түрде оңай орындалады, өйткені жаңа разрядты генерациялау үшін ауысым регистрінің тек екі битін XOR жасау керек (нөлдік термин ескерілмейді, яғни x0= 1, жоғарыдағы мысалды қараңыз). Шынында да, кестеде келтірілген барлық кері байланыс көпмүшеліктері сирек, яғни олардың коэффициенттері көп емес. Сиректік әрқашан әлсіздік көзі болып табылады, бұл кейде алгоритмді ашу үшін жеткілікті. Криптографиялық алгоритмдер үшін коэффициенттері көп тығыз қарабайыр көпмүшелерді қолданған әлдеқайда тиімді. Тығыз көпмүшеліктерді пайдалану арқылы, әсіресе кілттің бөлігі ретінде, әлдеқайда қысқа PrCcLOC пайдалануға болады.
Тығыз қарабайыр көпмүшелердің модулі 2 құру оңай емес. Жалпы жағдайда k дәрежелі қарабайыр көпмүшелерді құру үшін 2 санын көбейткіштерге бөлуді білу керек.
к- 1.
Зертхана №12125

Өздігінен PgCsLOS жақсы псевдокездейсоқ реттілік генераторлары болып табылады, бірақ олардың кейбір жағымсыз кездейсоқ емес (детерминирленген) қасиеттері бар. Тізбектелген биттер сызықты, сондықтан оларды шифрлау үшін жарамсыз етеді. Ұзындығы n RgCsLOS үшін ішкі күй генератордың алдыңғы n шығыс разряды болып табылады. Кері байланыс схемасы құпия сақталса да, оны жоғары тиімді Берлекамп-Масси алгоритмі арқылы генератордың 2n шығыс разрядтарынан анықтауға болады.
Сонымен қатар, осы тізбектің дәйекті биттерін пайдаланып жасалған үлкен кездейсоқ сандар жоғары корреляцияға ие және қолданбалардың кейбір түрлері үшін мүлдем кездейсоқ емес. Осыған қарамастан, RgSsLOS шифрлау жүйелері мен алгоритмдерінің құрамдас бөліктері ретінде жиі пайдаланылады.
-
RgCsLOS негізіндегі ағындық шифрлар. PrCsLOS негізіндегі кілттер ағыны генераторын жобалаудың негізгі тәсілі қарапайым. Алдымен бір немесе бірнеше PrCsLOS алынады, әдетте ұзындығы әртүрлі және кері байланыс көпмүшелері әртүрлі. Егер ұзындықтар салыстырмалы жай болса және барлық кері байланыс көпмүшелері қарабайыр болса, онда алынған генератор максималды ұзындыққа ие болады. Кілт RgSsLOS регистрлерінің бастапқы күйі болып табылады. Әр жолы жаңа бит алу үшін RgCsLOS регистрлерін битке жылжыту жеткілікті (бұл кейде тактілік деп аталады). Шығыс биті RgCsLOS регистрлерінің кейбір биттерінің функциясы, жақсырақ сызықты емес. Бұл функция біріктіруші функция деп аталады, ал генератор тұтастай біріктірілген генератор деп аталады. Егер шығыс биті бір PrCsLOS функциясы болса, онда генератор сүзгі генераторы деп аталады. Бұл құрылғылардың артындағы теорияның көп бөлігін Селмер және Нил Зиерлер әзірледі. Сіз бірқатар асқынуларды енгізе аласыз. Кейбір генераторларда әртүрлі PgCsLOS үшін әртүрлі тактілік жиіліктер қолданылады, кейде бір генератордың жиілігі екіншісінің шығысына байланысты болады. Бұлардың барлығы сағатпен басқарылатын генераторлар деп аталатын Екінші дүниежүзілік соғысқа дейінгі шифрлық машина идеяларының электронды нұсқалары. Сағатты басқару бір PgSsLOS шығысы басқа PgSsLOS тактілік жылдамдығын басқаратын алға бағытталуы немесе бір PgSsLOS шығысы өз сағатын басқаратын жабық цикл болуы мүмкін. Бұл генераторлардың барлығы, кем дегенде, теориялық тұрғыдан, ұя салу шабуылдарына және ықтимал корреляцияға сезімтал болғанымен, олардың көпшілігі әлі де қауіпсіз.
1263-БӨЛІМ

Бұрынғы Кембридждегі таза математика кафедрасының меңгерушісі және Блетчли паркінде криптоаналитик болған Ян Касселс «криптография – математика мен шатасудың қоспасы, сондықтан математиканы шатастырусыз сізге қарсы қолдануға болады» деді. Оның айтқысы келгені: ағындық шифрларда PrCcLOC сияқты белгілі бір математикалық құрылымдар максималды ұзындықты және басқа қасиеттерді қамтамасыз ету үшін қажет, бірақ кез келген адамның тізілім мазмұнын алуына және бұзуына жол бермеу үшін кейбір күрделі сызықты емес тәртіпсіздіктер енгізілуі керек. алгоритм. Бұл кеңес блок алгоритмдері үшін де жарамды.
Көптеген нақты ағындық шифрлар PrCsLOS негізінде жасалған. Электрониканың алғашқы күндерінің өзінде оларды құрастыру оңай болды. Ауысым регистрі биттердің массивінен басқа ештеңе емес, ал кері байланыс тізбегі XOR қақпаларының жиынтығы болып табылады. Қазіргі заманғы интегралды схемаларды пайдаланған кезде де, PgCsLOS негізіндегі ағындық шифр бірнеше логикалық қақпалардың көмегімен айтарлықтай қауіпсіздікті қамтамасыз етеді. PgCsLOS мәселесі
-
олардың бағдарламалық қамтамасыз етуді енгізу өте тиімсіз екенін. Сіз сирек кері байланыс полиномдарынан аулақ болуыңыз керек - олар корреляциялық шабуылдарды жеңілдетеді - және тығыз кері байланыс полиномдары тиімсіз.
Криптографияның бұл саласы қарқынды дамып келеді және NSA тарапынан мұқият үкімет бақылауында. Әзірлеулердің көпшілігі жіктеледі - бүгінгі күні қолданылатын көптеген әскери шифрлау жүйелері PrCsLOS негізінде жасалған. Шынында да, Cray компьютерлерінің көпшілігінде (Cray 1, Cray X-MP, Cray Y-MP) әдетте «халық саны» деп аталатын өте қызықты нұсқау бар. Ол регистрдегі 1 санын санайды және екі екілік сөз арасындағы Хэмминг қашықтықты тиімді есептеу үшін де, PrCsLOS векторланған нұсқасын жүзеге асыру үшін де пайдаланылуы мүмкін. Бұл нұсқаулық NSA-ның канондық нұсқауы болып саналады және барлық дерлік компьютерлік келісімшарттарда кездеседі.
-
екінші жағынан, күрделі болып көрінетін ауысымдық регистр генераторларының таңқаларлық үлкен саны бұзылды.
PgCsLOS жалған кездейсоқ сандар тізбегінің сызықтық күрделілігі туралы. Ағындық шифрларды талдау блоктық шифрларға қарағанда жиі оңайырақ. Мысалы, PgCsLOC негізіндегі генераторларды талдау үшін пайдаланылатын маңызды параметр сызықтық күрделілік немесе сызықтық интервал болып табылады. Ол шығуды имитациялай алатын ең қысқа PgCsLOS n ұзындығы ретінде анықталады.