ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 1051
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Еще пример задания:
Р-12. Запись числа 38110 в системе счисления с основанием N оканчивается на 3 и содержит 3 цифры. Укажите наибольшее возможное основание этой системы счисления N.
Решение:
-
поскольку запись в системе счисления с основанием N заканчивается на 3, то остаток от деления числа 381 на N равен 3, то есть при некотором целом имеем
имеем
-
следовательно, основание N – это делитель числа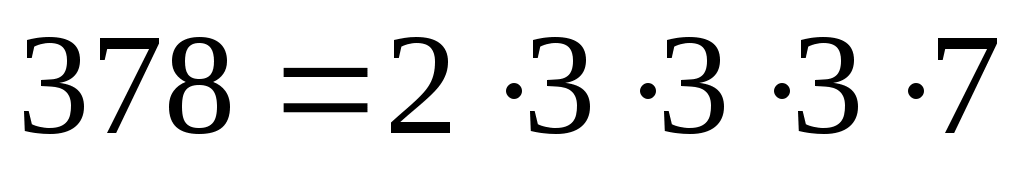
-
с другой стороны, запись числа содержит 3 цифры, то есть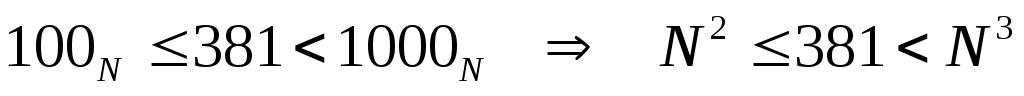
-
неравенство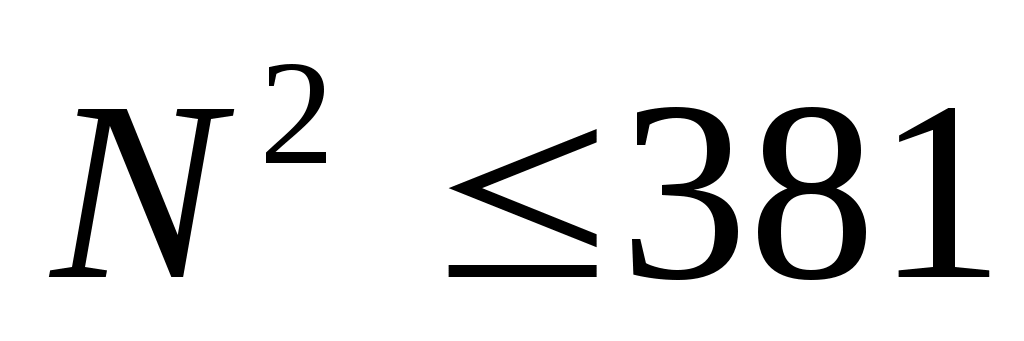 дает
дает 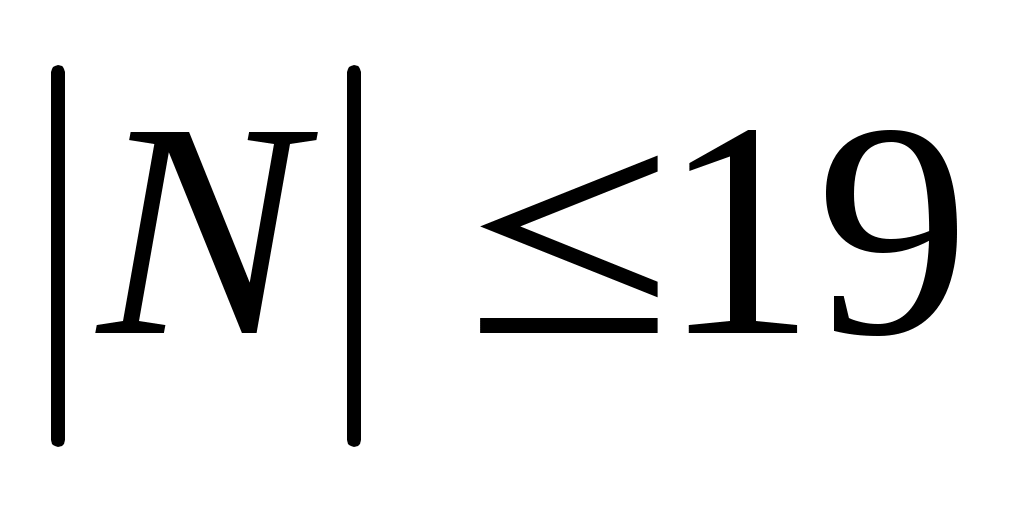 (так как
(так как 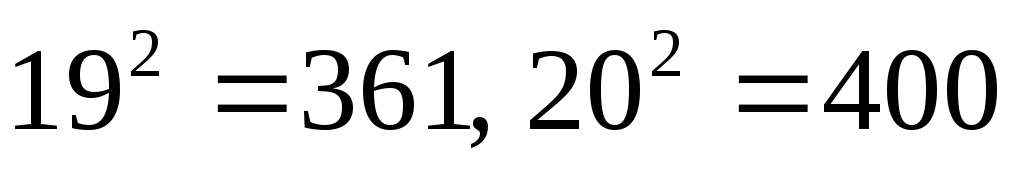 )
) -
неравенство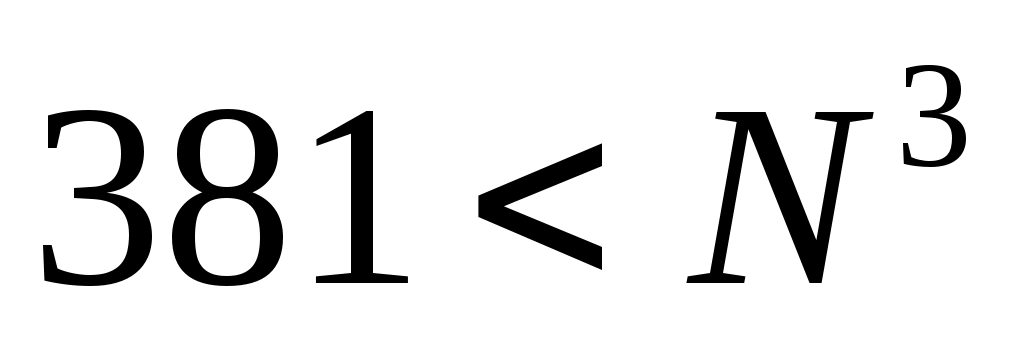 дает
дает 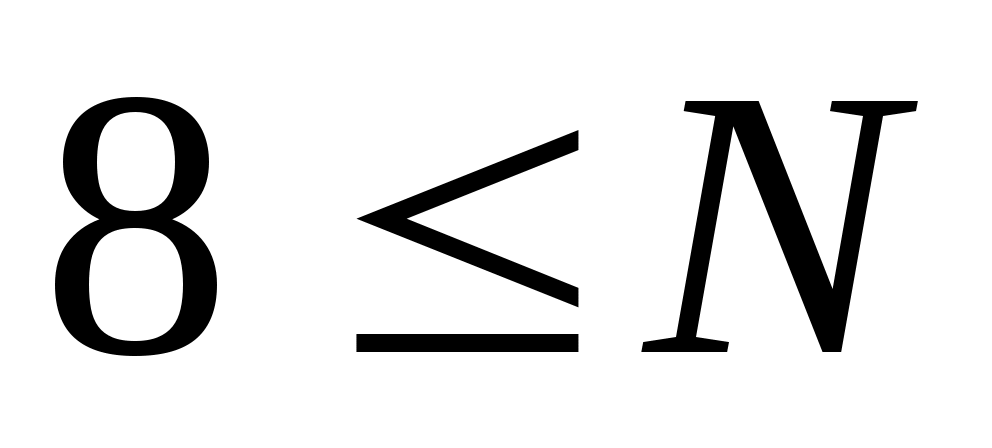 (так как
(так как 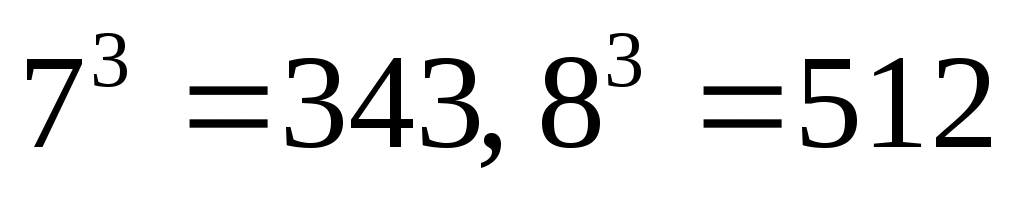 )
) -
таким образом,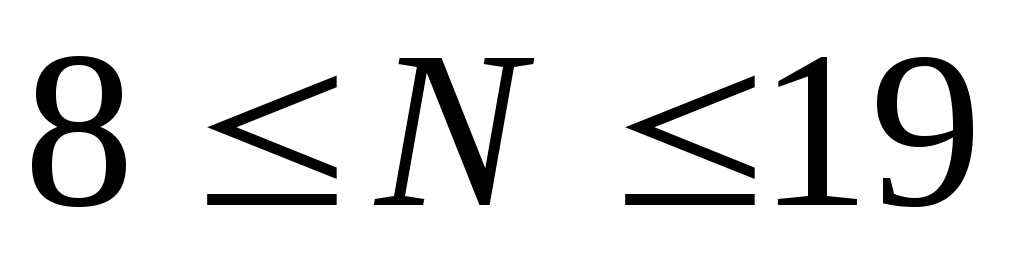 ; в этом диапазоне делителями числа 378 являются числа
; в этом диапазоне делителями числа 378 являются числа
-
9, при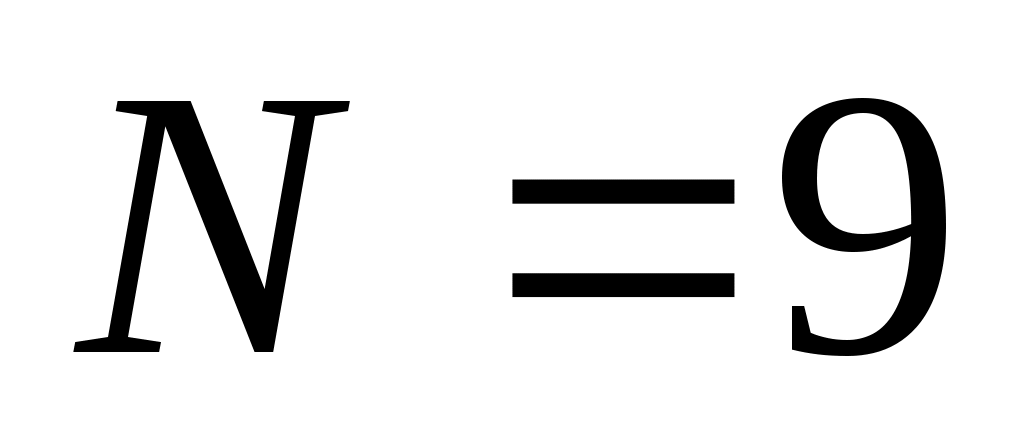 получаем запись числа
получаем запись числа 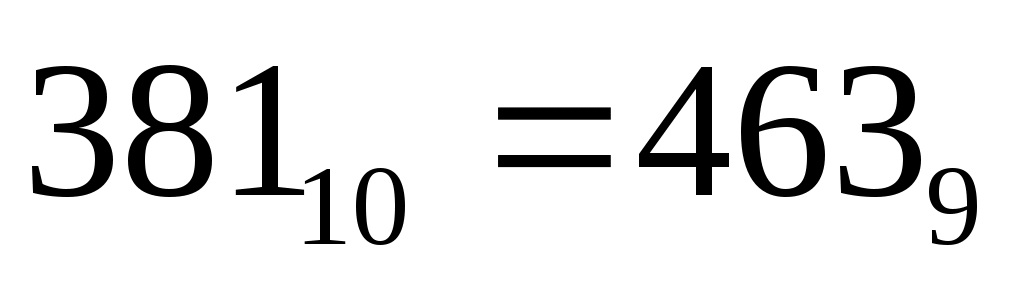
-
14, при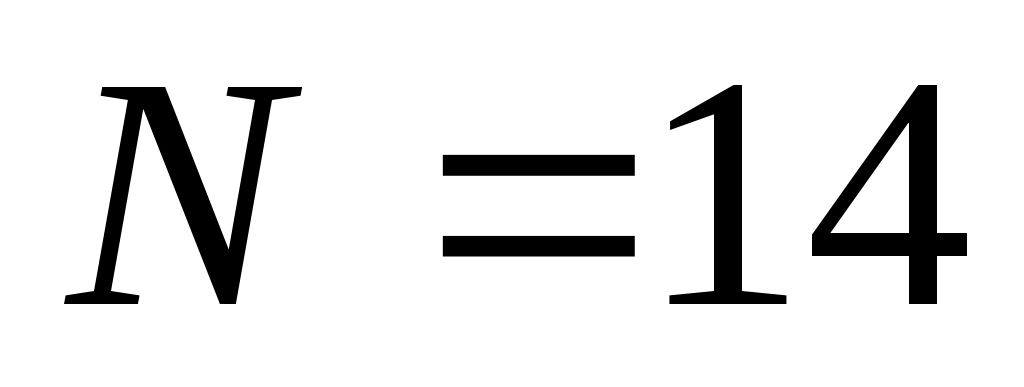 получаем запись числа
получаем запись числа 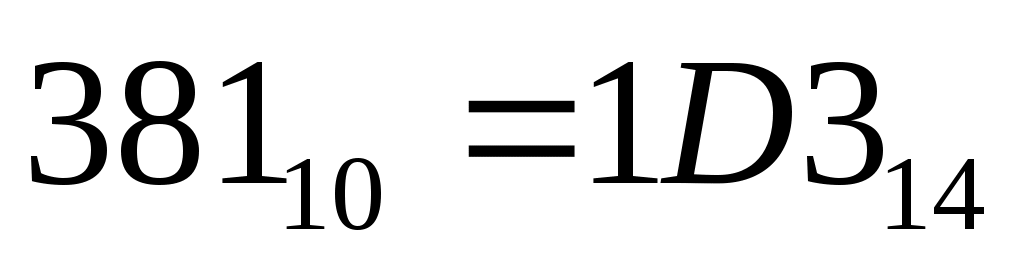
-
18, при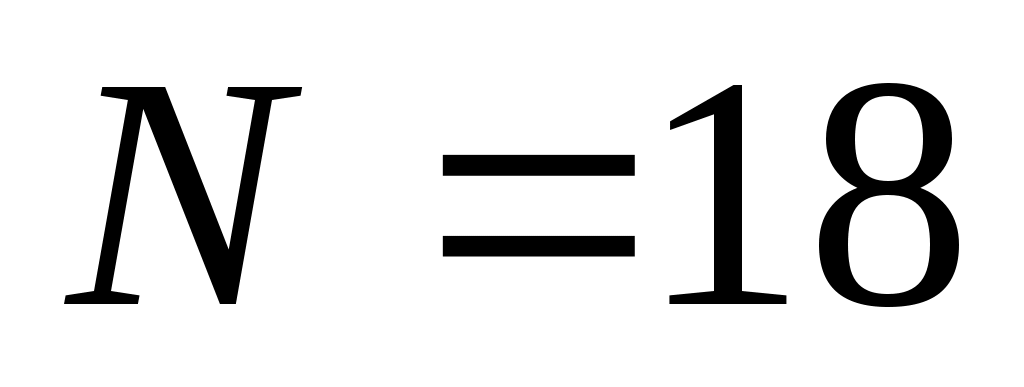 получаем запись числа
получаем запись числа 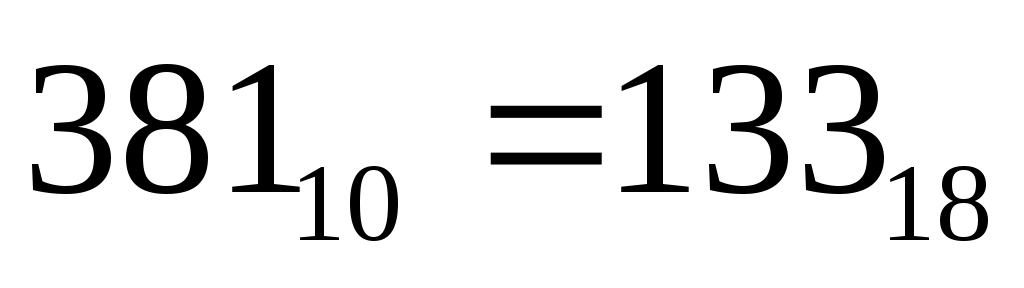
наибольшим из приведенных чисел – это 18 (можно было сразу искать подбором наибольший делитель числа 378, начиная с 19 «вниз», на уменьшение)
таким образом, верный ответ – 18.
Решение (программа на
Python, А.Н. Носкин):
-
можно решить задачу с помощью программы:
for i in range(100,1,-1):# перебираем возможные основания
x = 381
x_N = ''
while x > 0:# перевод в N-ю систему
if x%i>9:break # пропускаем цифры в виде букв
else: x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N == '': pass
elif x_N[-1]== "3" and len(x_N) == 3:
print(i)
break
-
ответ: 18.
Решение (программа на Python, Б.С. Михлин):
-
Если цифры больше девяти не представлять латинскими буквами, то программа даст неверный ответ 27, т.к. 381 в 27-ичной системе не (14)3, а E3 (т.е. двухзначное число)
for N in range(36, 3, -1): # подбираем основание N от 36 до 4
x = 381
s = ''
while x:
d = x % N # цифра (digit)
if d < 10:
d = str( d ) # цифра от 0 до 9
else:
d = chr( ord( 'A' ) + d - 10 ) # буквенная цифра от A до Z
s = d + s # цифру d приписываем слева
x //= N
if s[-1] == '3' and len( s ) == 3:
print( N )
break
-
ответ: 18.
Еще пример задания:
Р-11. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход:
-
вспомним алгоритм перевода числа из десятичной системы в систему с основанием (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на  , а две младших цифры – это остаток от деления на
, а две младших цифры – это остаток от деления на  и т.д.
и т.д. -
в данном случае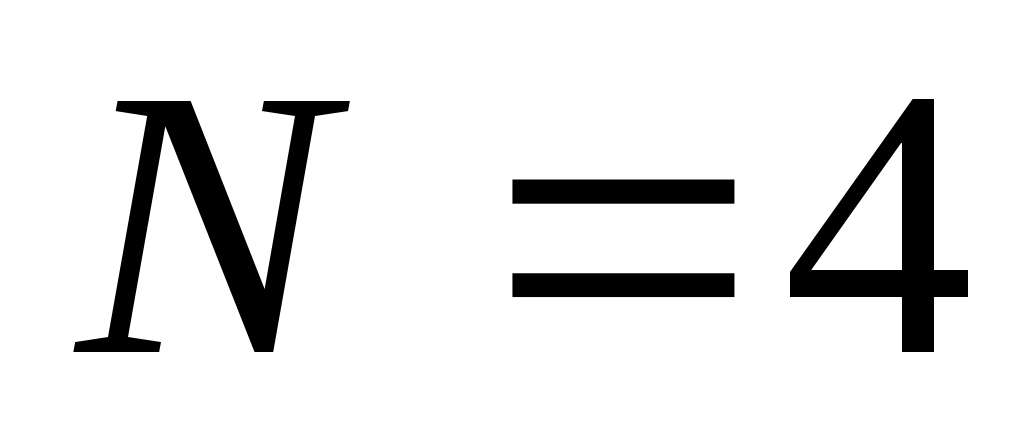 , остаток от деления числа на
, остаток от деления числа на 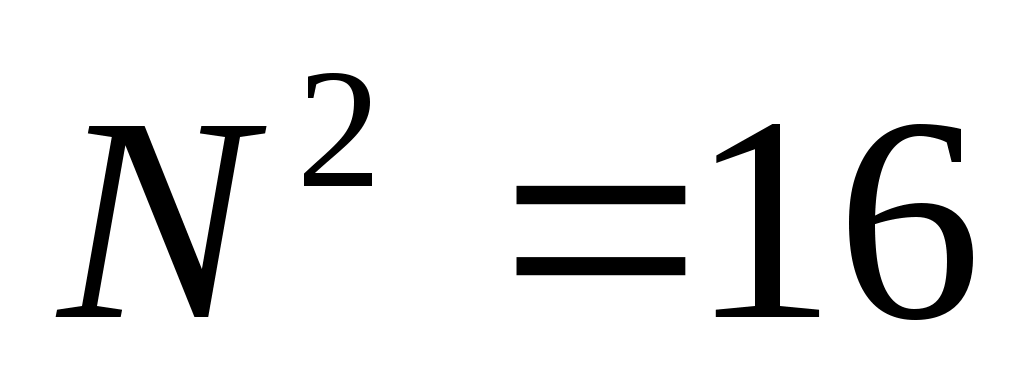 должен быть равен 114 = 5
должен быть равен 114 = 5 -
потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16
Решение (вариант 1, через десятичную систему):
-
общий вид чисел, которые дают остаток 5 при делении на 16:
где
-
среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при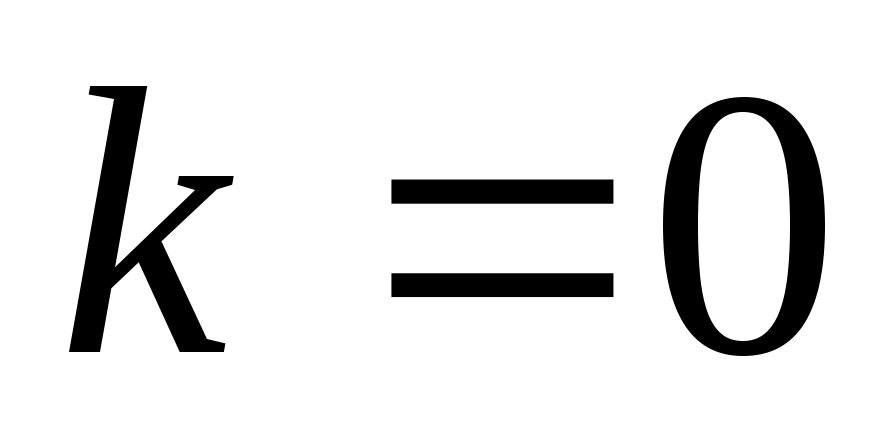 ) и 21 (при
) и 21 (при 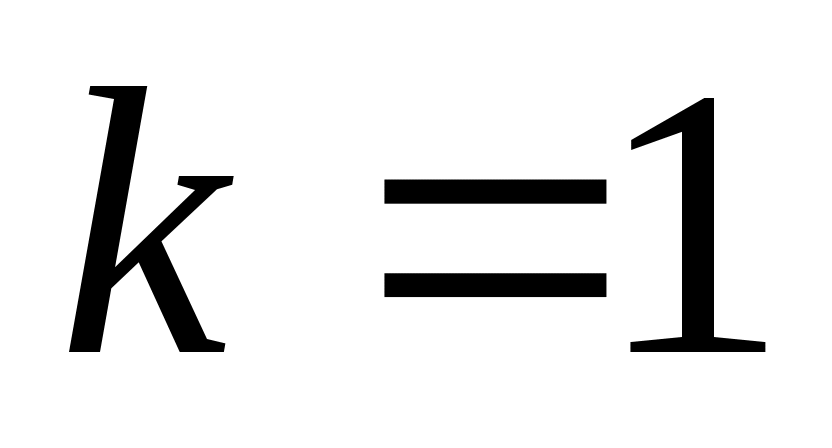 )
) -
таким образом, верный ответ – 5, 21 .
-
Возможные ловушки и проблемы:-
выражение «не превосходящие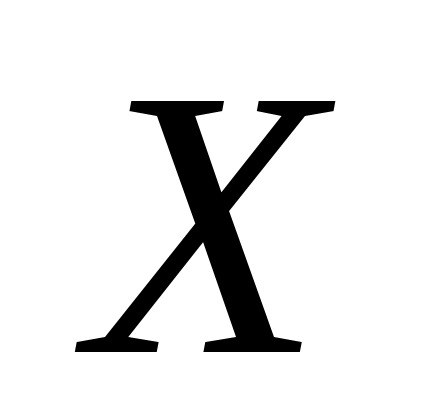 » означает «меньшие или равные
» означает «меньшие или равные 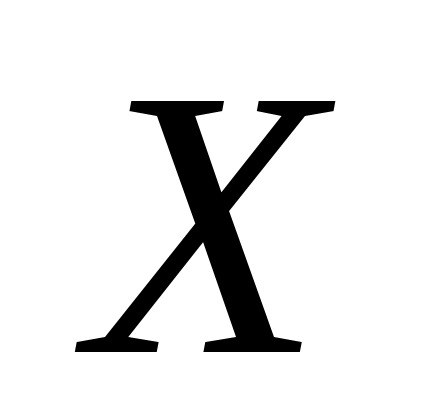 », а не строго меньшие
», а не строго меньшие 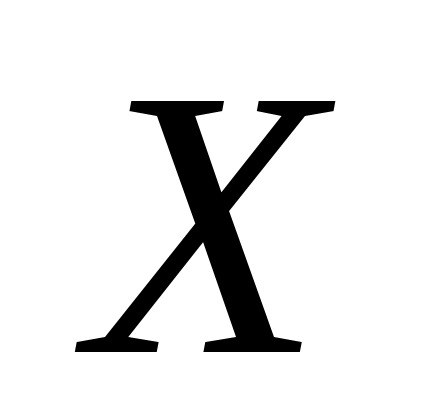
-
остаток, состоящий из нескольких цифр (здесь – 114), нужно не забыть перевести в десятичную систему -
найденные числа нужно записать именно в порядке возрастания, как требуется
-
Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):
-
переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения -
из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21 -
таким образом, верный ответ – 5, 21 .
-
Возможные ловушки и проблемы:-
есть риск случайно «забыть» какое-то число или найти «лишнее» (в данном случае – большее 25) -
можно сделать ошибки при переводе чисел из четверичной системы в десятичную или вообще «забыть» перевести
-
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу с помощью программы:
for i in range(1,31):# перебираем ответы
x = i
x4 = ''
while x > 0:# перевод в 4-ю систему
x4 += str(x%4)
x //=4
x4 = x4[::-1]# разворот числа
if x4[-2:]== "11":
print(i, end=",")
-
ответ: 5, 21.
Решение (программа на Python, Б.С. Михлин):
-
полная программа:
for d in '0', '1': # d - цифра (digit). При d > 1 - выход за 25
# int - переводит из 4-ой в 10-ую систему
print( int( d+'11', 4 ), end = ',' )
-
Ответ: 5, 21.
Еще пример задания:
Р-10. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Общий подход:
-
здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через
-
поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть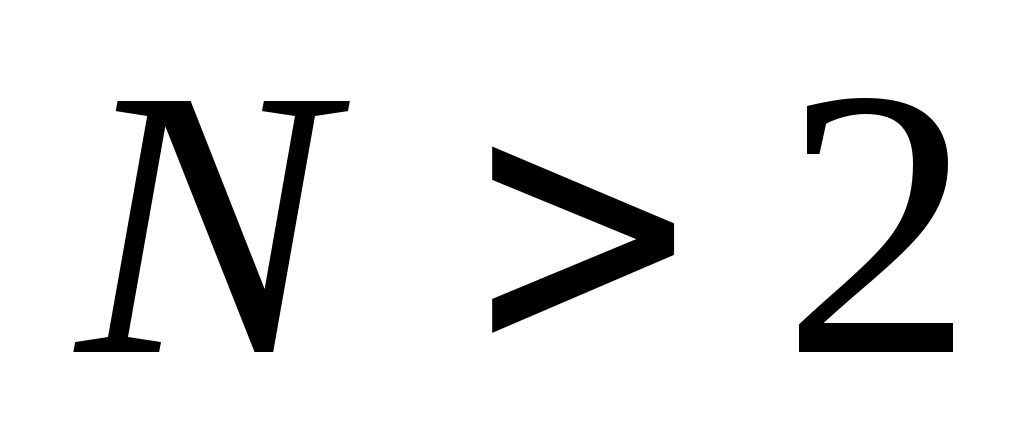
-
вспомним алгоритм перевода числа из десятичной системы в систему с основанием (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на
(см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на 
Решение:
-
итак, нужно найти все целые числа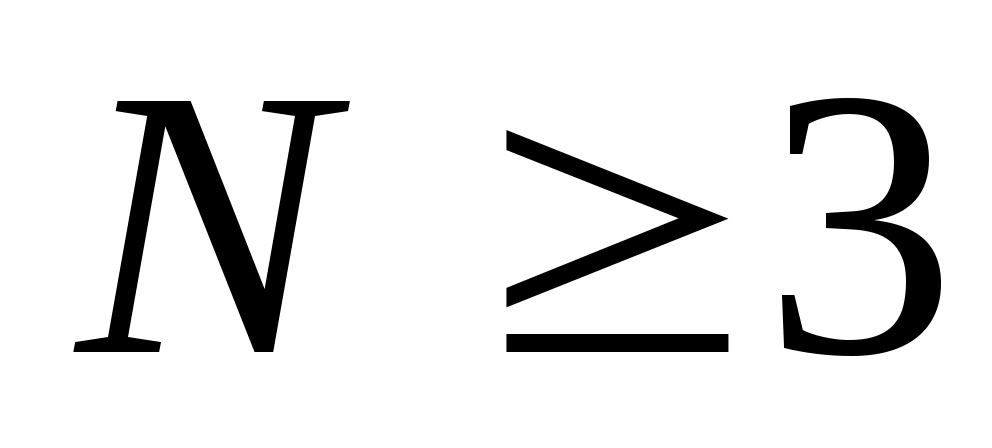 , такие что остаток от деления 23 на
, такие что остаток от деления 23 на  равен 2, или (что то же самое)
равен 2, или (что то же самое)
где
-
сложность в том, что и , и
, и  неизвестны, однако здесь нужно «играть» на том, что это натуральные числа
неизвестны, однако здесь нужно «играть» на том, что это натуральные числа -
из формулы (*) получаем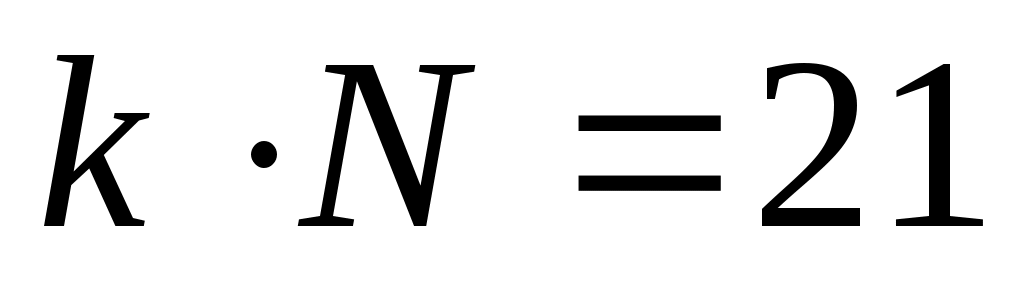 , так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2
, так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2 -
в этой задаче есть только три таких делителя: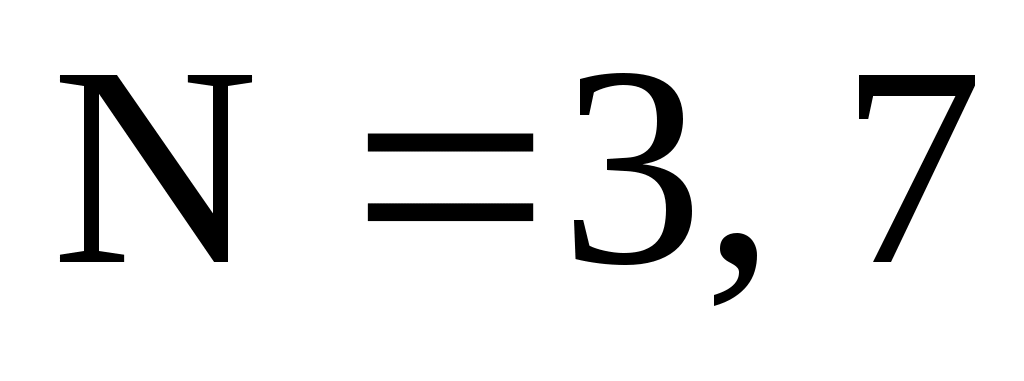 и
и 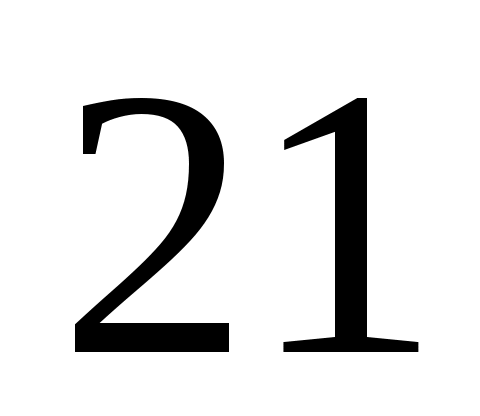
-
таким образом, верный ответ – 3, 7, 21 .