Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 130
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
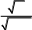
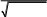
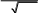
Примеры выполнения задания.
Пример 1.
ex2 dx
0
Задача 1. Подберем число A так, чтобы интеграл
числить приближенно с точностью до 0.0001.
ex2 dx
0
можно было вы-
Из неравенства Тогда
x2 2Ax A2 (x A)2 0
следует
x2 2Ax A2 .
2 Ax2 A2
-
A2
ex2 dx
e2 Ax A2 dx eA2 e2 Axdx eA2 e
eA2 e e.
A A A
e32
2A A
2A 2A
Легко проверить, что
0.00005 .
2 3 2Очевидно, что достаточно взять
A 3.
3
ex2 dx ex2 dx ex2 dx.
0 0 3
Задача 2. Теперь вычислим с помощью метода трапеций (или другого выше
3
рассмотренного) определенный интеграл e x2 dx. Верхний предел оценен
0
выше.
Результат вычисления: 0.8861936233658585. Отрезок интегрирования был разбит на 3 части.
3
Задача 3. Вычислим интеграл e x2 dx
0
с помощью встроенной функции
romberg.
Оценим остаток несобственного интеграла ex2 dx
3
с помощью встроенного
пакета quadpack.
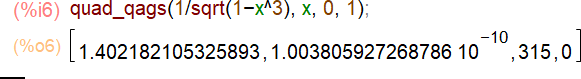
Как мы видим, результат 1.957719323677975*10^-5, что меньше 0.00005.
Пример 2.
0.5
dx
0
Задача 1. Найдем такое положительное число , чтобы интеграл
0.5 dx
был вычислен с точностью до .0
Точкой бесконечного разрыва подынтегральной функции является
концевая точка
x 0. Найдем искомое значение , для которого выполняет-
ся неравенство (4.2) для левого конца:
f xdx
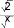0 . (4.3)
2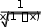
Так как при
x0;0.5, то
dx
2 dx
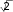2 2 .
0
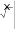
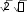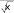0 0 Тогда для выполнения неравенства (4.3) необходимо, чтобы Возьмём 0.005, значит, 0.00000078125 .
2
.
32
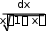
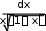
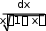0.5 0.00000078125 0.5
0 0 0.00000078125
Задача 2. Вычислим с помощью метода средних прямоугольников (или дру-
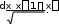0.5гого выше рассмотренного) определенный интеграл
0.00000078125
Отрезок интегрирования был разделен на 621 часть. Результат вычис- ления 1.558566890295938.
Задача 3. Проверим полученный результат. Проинтегрировать несобствен- ный интеграл с помощью встроенной функции romberg невозможно. Приме- ним встроенный пакет вычислений quadpack.
В ячейке вывода массив результата вычисления содержит: 1.570796326794895– приближённое значение интеграла; 5.454703355667334*10^-11– относительная погрешность вычислений; 315 – число интервалов разбиения;
0 – признак корректности вычислений (0 – без проблем).
Список литературы
-
Фихтенгольц, Г. М. Курс дифференциального и интегрального исчис- ления : учебник для вузов : в 3 томах / Г. М. Фихтенгольц. — 15-е изд., стер.
— Санкт-Петербург : Лань, [б. г.]. — Том 1 — 2021. — 608 с. — ISBN 978-5- 8114-7061-7. — Текст : электронный // Лань : электронно-библиотечная си- стема. — URL: https://e.lanbook.com/book/154399. — Режим доступа: для ав- ториз. пользователей.
-
Фихтенгольц, Г. М. Курс дифференциального и интегрального исчис- ления : учебник для вузов : в 3 томах / Г. М. Фихтенгольц. — 15-е изд., стер.
-
Санкт-Петербург : Лань, [б. г.]. — Том 2 : Курс дифференциального и ин- тегрального исчисления — 2021. — 800 с. — ISBN 978-5-8114-7377-9. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/159505. — Режим доступа: для авториз. пользова- телей.
-
Фихтенгольц, Г. М. Курс дифференциального и интегрального исчис- ления : учебник для вузов : в 3 томах / Г. М. Фихтенгольц. — 11-е изд., стер.
— Санкт-Петербург : Лань, 2020 — Том 3 — 2020. — 656 с. — ISBN 978-5- 8114-6652-8. — Текст : электронный // Лань : электронно-библиотечная си- стема. — URL: https://e.lanbook.com/book/149365. — Режим доступа: для ав- ториз. пользователей.
-
Берман, Г. Н. Сборник задач по курсу математического анализа / Г. Н. Берман. — 11-е изд., стер. — Санкт-Петербург : Лань, 2023. — 492 с. — ISBN 978-5-507-46033-5. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/295943 (дата обращения: 07.03.2023). — Режим доступа: для авториз. пользователей. -
Демидович, Б. П. Основы вычислительной математики : учебное посо- бие / Б. П. Демидович, И. А. Марон. — 8-е изд., стер. — Санкт-Петербург : Лань, 2022. — 672 с. — ISBN 978-5-8114-0695-1. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/210674 (дата обращения: 07.03.2023). — Режим до- ступа: для авториз. пользователей. -
Демидович, Б. П. Сборник задач и упражнений по математическому анализу : учебное пособие для вузов / Б. П. Демидович. — 24-е изд., стер. — Санкт-Петербург : Лань, 2022. — 624 с. — ISBN 978-5-8114-9078-3. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/184105 (дата обращения: 07.03.2023). — Режим до- ступа: для авториз. пользователей. -
Марон, И. А. Дифференциальное и интегральное исчисление в приме- рах и задачах. Функции одной переменной : учебное пособие / И. А. Марон.