Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 131

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

«ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ»




студенту гр.




(фамилия, имя, отчество)

Тема работы: «Приближенные методы вычисления интегралов» Входные данные: (формулировка всех заданий варианта)

Задание получил

(подпись) (дата)



График выполнения работы:
Замечания консультанта







К защите. Руководитель работы

(подпись) (дата)

  1. Приложение определенных интегралов.

    1. Площадь плоской фигуры


  1. Если

f(x) 0

на [a,b] , то интеграл

b

f xdx

a

геометрически представляет

собой площадькриволинейнойтрапеции,которая ограничена графиком

функции

y f(x), прямыми x a, x bи осью Ox, т.е.

b

S f xdx

a

  1. Пусть криволинейная трапеция ограничена слева и справа прямыми x a,

x b, сверху - графиком функции f x , снизу - графиком функции g x .


b

Тогда площадь фигуры, ограниченной данными линиями вычислим по формуле:

S f x g xdx.

a
Пример 1. Вычислить площадь фигуры, ограниченной линиями:

1) y x2 2x 4 ,

y 3,

x 1

Построим графики данных функций. Найдем точку пересечения прямой
y 3
и параболы
y x2 2x 4 . Для

этого приравняем значения y: 3 x2 2x 4 . Отсюда получаем

x2 2x 1 0 , x12 0 ,

x1. При

этом Если

y 3.
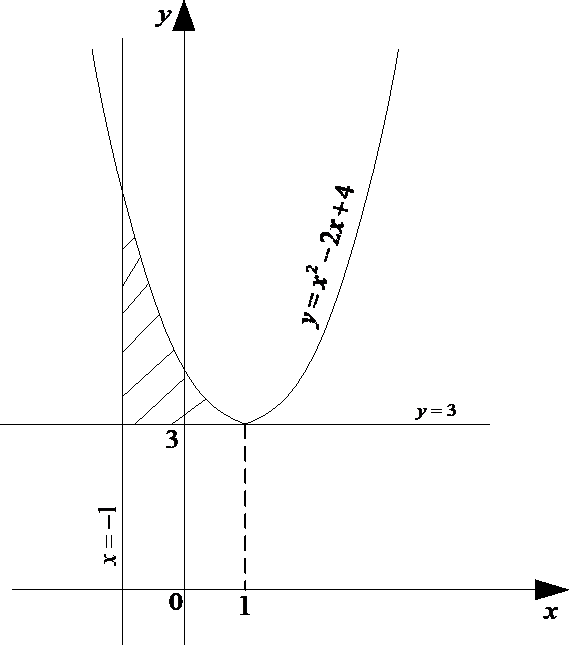x 1, то

y (1)2 2 (1) 4 7 .

Найдем вершину параболы:

x b 2 1, y1 3- это точка

2a 2

пересечения прямой и параболы. Строим область, площадь которой надо вычислить:


b

Тогда площадь фигуры, ограниченной данными линиями вычислим по формуле:

S f x g xdx,

a

где

f x x2 2x 4

- уравнение линии, которая ограничивает фигуру

сверху, а

g x 3

ограничивает снизу,

x[1,1].




S x2 2x 4 3dx x2 2x 1dx x12 dx

1
Итак,

1


3
S8 ед2 .

1


3
 1


x1
3


1


1
1 0 8 8 . 3 3


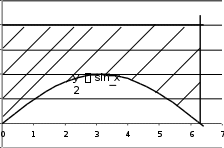
  1. y sin x,

2

y 2 ,

x 0,

x 2 .

Построим чертеж.
2,5
2

x 2
1,5
1
0,5
0
-0,5



2 2
2

x 

x2

S 2 sin dx 2x 2cos

0    0

4 2 2 4 4 ,

т.е. S 4 4ед2 .
3) y 2x2 8x 4 , y x2 x 4 .

y 2x2 8x 4 - парабола, ветви направлены вверх, y x2 x 4 -

парабола, ветви направлены вниз. Значит, фигура ограниченна сверху

параболой

y x2 x 4 , а снизу параболой

y=2x2 8x 4 .

Найдем точки пересечения линий:

2x2 8x 4 x2 x 4 ,

3x2 9x 0 ,

3x x 3 0 ,

откуда

x1 0 ,

x2 3.

Вычислим значения ординат: при

x1 0

получаем

y1 4 , при

x2 3

получаем

y2 2 .

Построим графики парабол и найдем область, площадь которой надо вычислить:


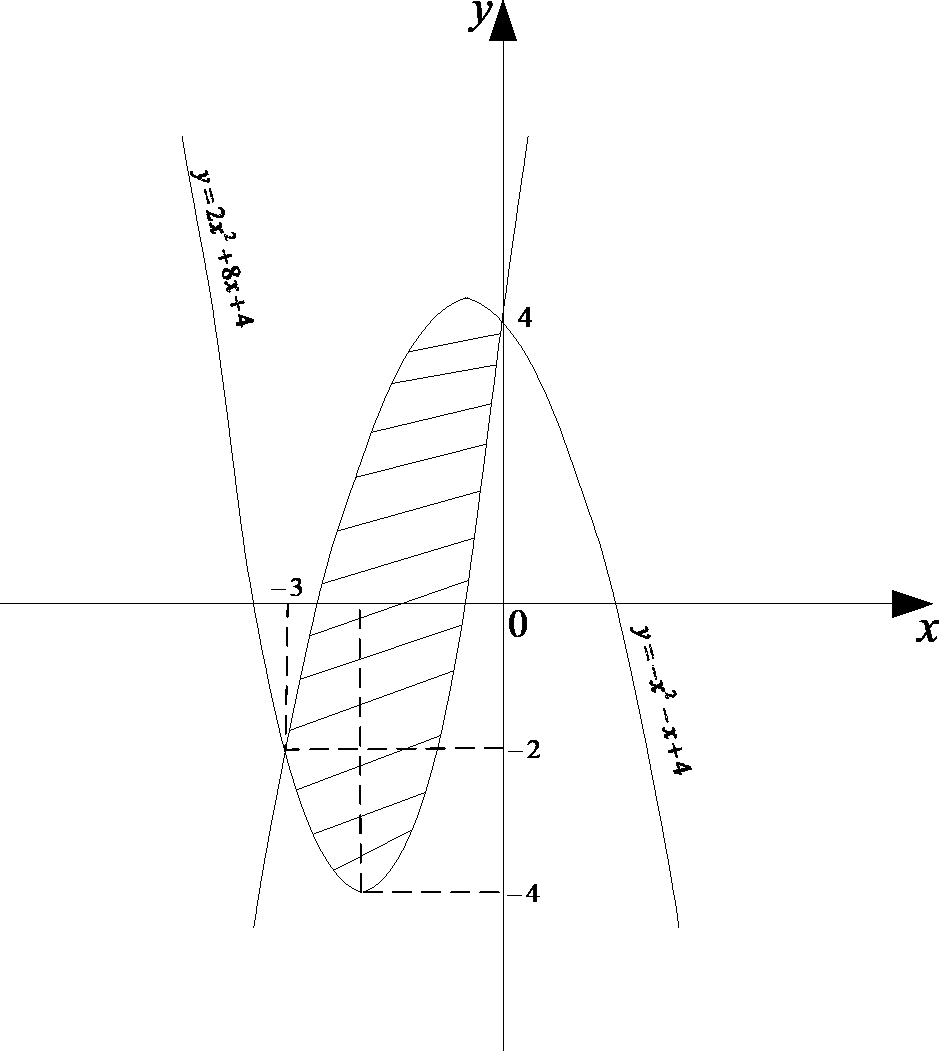
Найдем площадь фигуры:

0 0
9 0

S x2 x 4 2x2 8x 4dx 3x2 9xdx x3

x2

3 3

2 3
0 27 81 27 ,

2 2


т.е.

 


2
S27 ед2 .

Для решения подобных задач в Maxima следует выполнить следующиедействия:

    1. Изобразить кривые, которые задают рассматриваемый объект.

    2. Найти точки пересечения этих кривых.

    3. При необходимости разбить фигуру на области.

    4. Вычислить определенные интегралы с помощью программы Maxi- ma и вручную.

    5. Записать ответ.

Пример 2. Вычислить площадь фигуры, ограниченной следующими линиями

y 3x x2 и y x2 x.

Зададим функции и построим графики:




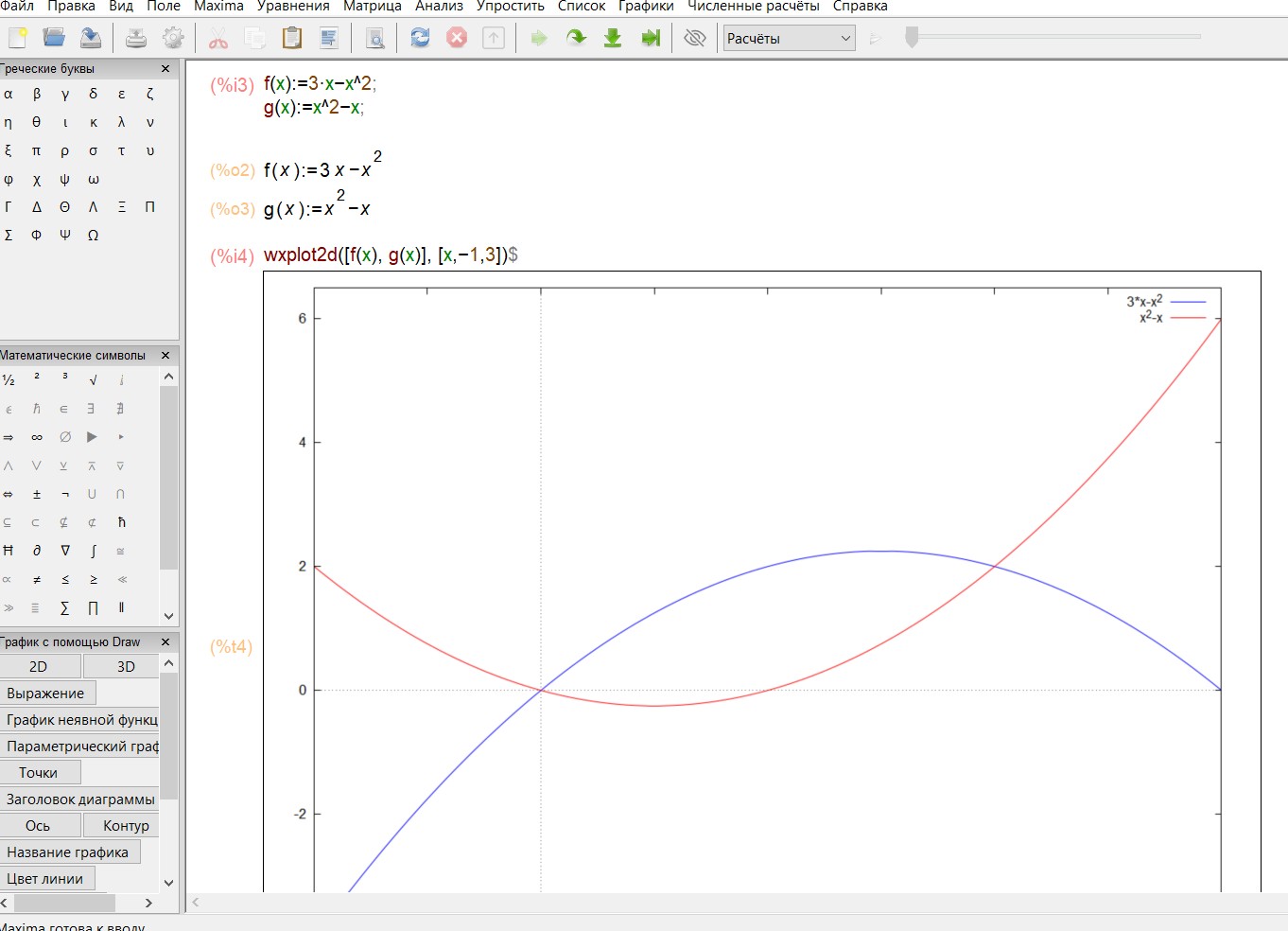
Из графика видно, что функции пересекаются в двух точках, и об- ласть является простой, т.е. ее не нужно делить на подобласти.

Найдем точки пересечения кривых, затем составим и вычислим определен- ный интеграл, результат которого и есть площадь данной фигуры



Смотрите также файлы