Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 129
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
f xdx,
b
S2
f xdx
a c2
могут быть вычислены с помощью любого из рассмотренных выше методов с
точностью до
y
каждый.
4
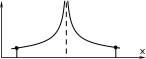
y0 a c
а
b 0 a c b
б
Рис. 7. Подынтегральная функция обращается в бесконечность в некоторой точке отрезка интегрирования:
а) с двух сторон от нее; б) с одной стороны от нее.
Для приближенного вычисления сходящегося несобственного инте-
грала с заданной точностью выбирают положительные числа 1 и 2
малыми, чтобы имело место неравенство
столь
c2
c1
f xdx
2(4.2)
Тогда
b
f(x)dx S1 S2
a
с точностью до .
Если точка разрыва подынтегральной функции является концевой для отрезка интегрирования a,b, то методика вычисления интеграла очевидным
образом видоизменяется.
-
Интегралы с бесконечными переделами
Рассмотрим интеграл с бесконечной границей интегрирования, напри-
мер
fxdx. По определению
a
f xdx
a
A
lim f xdx
A
a
Один из универсальных способов вычисления подобных интегралов заключается в их представлении в виде суммы двух интегралов:
A
f xdx fxdx f xdx,
a a A
где A– некоторое большое положительное число, рис. 8.
yy fx
x
0 a A
Рис. 8. Иллюстрация вычисления интеграла с бесконечной границей интегрирования.
Вычисление первого интеграла на конечном отрезке a, A не вызывает затруднений. Он может быть вычислен с помощью любого из рассмотренных
выше методов с точностью до .
2
Выбор числа Aпроизводят таким образом, чтобы
f xdx .
A 2Замечание. В некоторых случаях при вычислении несобственных интегралов подходящая замена переменной интегрирования позволяет вообще избавиться от рассмотренных выше особенностей. Так, например, при
1 cos x
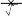вычислении интегралаI
0
dxимеется особенность в точке
x 0, где
подынтегральная функция обращается в бесконечность. С помощью заменый
переменной
x t2 ( dx 2tdt) приходим к интегралу
1
I 2cos t2dt,
0
который не имеет особенностей и вычисляется с требуемой точностью с
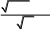
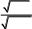
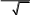
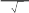применением любого из рассмотренных в данной главе методов.ЗАДАНИЕ 3
Задача 1. Представить интеграл в виде суммы двух интегралов. Найти пределы интегрирования, позволяющие вычислить интеграл с точностью до
0.005 для нечетных вариантов, до 0.0001 для четных вариантов.
Задача 2. Вычислить несобственный интеграл приближенно.
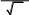Задача 3.Проверить результат вычислений с помощью встроенных функций программы wxMaxima.| 1 | 2 x 2 xdx 0 | 21 | 2 x 3 3 dx 0 8 x |
| 2 | arctgx x(2 x) dx 1 | 22 | arctgx 5 dx 1 x |
| 3 | 1 x3 3 3 x dx 0 | 23 | 3 2x1 4 x 2 dx 2 |
| 4 | dx e3 xx3 1 | 24 | dx x(1 x3) 1 |
| 5 | 1 3 x2 1 xdx 0 | 25 | 3 x 3 xdx 1 |
| 6 | arctgx 3 dx 1 1 x | 26 | arctgx x2 (1 x) dx 1 |
| 7 | 2 x2 x1 dx 1 | 27 | 0 x2 1 1 xdx 1 |
| 8 | dx 5 1 x x1 | 28 | dx exx x 1 |
| 9 | 0 4 x x2 5 2 dx 1 x | 29 | 1 1 x 3 dx 0 1 x |
| 10 | arctgx 3 2 dx 1 x x | 30 | arctgx x3 xdx 1 |
| 11 | 1 x2 2 3 x 1 dx 1 | 31 | 2 4 x3 4 x2 1 dx 1 |
| 12 | x2 x4 2 x3 dx 1 | 32 | dx 5 10 1 x x x 1 |
| 13 | 2 3 x2 4 2 xdx 1 | 33 | 0 dx 2 1 3 x(2 x) |
| 14 | arctgx x(1 x2 ) dx 1 | 34 | dx e2 xx2 1 |
| 15 | 2 x 2 4 3 dx 0 x | 35 | 1.5 dx 3 1 x1 |
| 16 | dx e4 xx4 1 | 36 | dx x2 x 1 1 |
| 17 | 1 2 x 4 dx 0 1 x | 37 | 2 x 2 dx 1 4 x |
| 18 | arctg2x 4 dx 1 4 x | 38 | xarctgx 2 x3 dx 1 |
| 19 | 1,5 dx 3 x(2 x) 0 | 39 | 0.5 dx 4 x(2 x) 0 |
| 20 | dx 3 2 1 x x 2 | 40 | x x 2 x3 dx 1 |