Задание. В какой координатной четверти расположены углы:



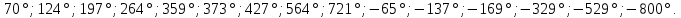
4.Изучение нового материала.

-Знаки тригонометрических функций:



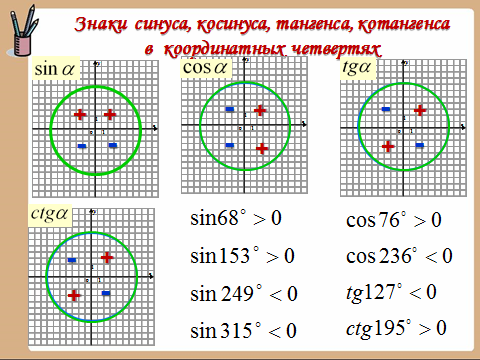
Задание.

Определить знак.





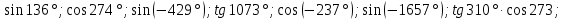
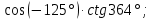
Определите знак



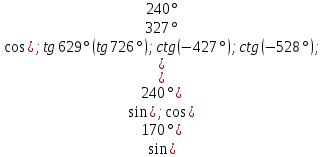
-Четность и нечетность функций:

1. 
   По единичной окружности устанавливаем равенства: , .
   
2. 
   Получаем , .
   
3. 
   Вывод: - четная функция, - нечетная функция, -нечетная функция, - нечетная функция.
   

- нечетная функция.

-Периодичность функции:

Еще одним из пунктов исследования функции является исследование функции на периодичность.
Функция называется периодичной, если существует такое число T, что для любого значения х из области определения функции .
Число T называют периодом функции. Например, известные нам тригонометрические функции являются периодическими, наименьший положительный период функций

---

y=sinxи y=cosx равен 2П, y=tgxиy=ctgx , наименьший положительный период которых равен П.

Работа с таблицей 278 учебника.

5. Зарядка для глаз.

6.Закрепление нового материала.

Решить №__________________

7.Самостоятельная работа с учеником с.245-249.

Разобрать примеры с решениями с.249-250.

Задание на повторение.

8.Итоги урока. Рефлексия. Д/з.

Выучить п.__, вопросы с._____. Сообщение « Из истории тригонометрии».

Решить №______________

Что вы узнали нового? На уроке:

• 
  вы рассматривали …
  
• 
  вы анализировали …
  
• 
  вы получили …
  
• 
  вы сделали вывод …
  
• 
  вы пополнили словарный запас следующими терминами …
  

---

Тема урока: «Графики функции у=sin x и у=соs x, их свойства»

Цели урока: Ознакомить учащихся со свойствами функции у=sin x и у=соs x, обучение построению графика функции у=sin x и у=соs x, чтению этого графика, использование свойств и графика функции у=sin x и у=соs x, при решении неравенств.

Задачи урока.

Образовательные – формировать умение построения графика функции у= sinx, рассмотреть свойства графика, формировать навыки свободного чтения графиков, умение считывать свойства функции по графику.

Развивающые – развивать логическое мышление, умение анализировать, обобщать полученные знания.

Воспитательные – активизировать интерес к получению новых знаний, воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.

Ход урока

1. Организационный момент. Приветствие.

2. Объявление темы и цели урока.

Тема урока: «Свойства функции у=sin x и ее график».

Сегодня рассмотрим свойства функции у=sinx и построим график. Рассмотрим простейшие преобразования функции, построим графики этих функций и перечислим их свойства.

3 Актуализация опорных знаний:

Выполнение устных упражнений.

Повторить определение тригонометрических функций и знаки значений этих функций.

Затем учащиеся отвечают на вопросы:

Учащимся предложена иллюстрация единичной окружности.

Вопросы:

• 
  При каких значениях х функция у=sinx принимает значение, равное 0? 1? -1?
  
• 
  Может ли функция у=sinx принимать значение больше 1, меньше -1?
  
• 
  При каких значениях х функция у=sinx принимает наибольшее (наименьшее) значение?
  
• 
  Каково множество значений функции у=sinx?
  

Дана иллюстрация единичной окружности.

Повторив знаки значений тригонометрических функций в каждой четверти координатной плоскости, учащимся предлагается показать несколько точек единичной окружности, соответствующих числам, синус которых положительное (отрицательное) число. Затем ответить на вопросы:

• 
  Какой знак имеет значение функции у = sinx?
  

если х = , х = ,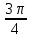

---

если 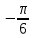х = , х = ?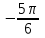

4. Изложение нового материала.

Обобщение и конкретизация знаний, полученных ранее: 1)область определения, 2)множества значений, 3)четность или нечетность, 4) периодичность,5) точки пересечения с осями координат, 6) промежутки знакопостоянства, 7) промежутки возрастания и убывания, 8) наибольшее и наименьшее значение функции. Выделенные характеристики позволят построить сначала часть графика функции у = sinx на отрезке 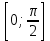, затем на отрезке 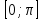, потом на отрезке 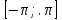и , наконец на всей числовой прямой.

Так как значение синуса - ордината соответствующей точки единичной окружности. Поскольку ординату можно найти для любой точки единичной окружности, то область определения функции у = sinx - все действительные числа. Это можно записать так: D (sinx)= R.

Для точек единичной окружности ординаты принимают все значения от -1 до 1, таким образом, для функции у = sinx область значений: у 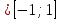. Это можно записать так: Е(sinx) = .

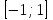Синус – нечетная функция: sin(-x) = - sinx. Поэтому ее график симметричен относительно начала координат.

Синус - периодическая функция с наименьшим положительным периодом Т = 2 : sin(x+2 ) = sinx. Таким образом, через промежутки длиной 2 вид графика функции sinx повторяется.

Чтобы найти точки пересечения графика функции с осями координат (на оси Оу значение х=0). Тогда соответствующее значение у =sin0=0, то есть график функции у = sinx проходит через начала координат. Функция обращается в нуль при х = k, при k .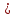

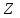Как видим, наибольшее значение функции sinx равно единице. Это значение достигается только тогда, когда соответствующей

---

точкой единичной окружности является точка, то есть при х = + 2 k, при k .

Наименьшее значение функции sinx равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка, то есть при х = - + 2 k, при k . А так же при х=

Для построения графика функции у = sinx на отрезке составим таблицу ее значений:

х	0
у= sinx	0		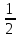		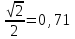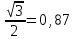1

Построим найденные точки и проведем через них кривую, учитывая, что на отрезке функция у = sinx возрастает. Получили график синуса на отрезке . Так как sin( -x) = sin( +x). То график синуса должен быть симметричен относительно прямой х =

---

Смотрите также файлы

• Рассчитаем срок между приобретением и датой погашения.docx

• Суммативное оценивание за раздел 4 а Химические элементы и соединения в организме человека.docx

• I ii iii iv iii ii i.doc

• Курсовая работа 1 по дисциплине Теоретические основы электротехники.docx

• По Л. Н. Толстому.docx