• 
  Изобразите в виде графиков тригонометрических функций смысл поговорки:
  
• 
  1) "Выше меры конь не скачет" у=|cos x| или y=|sin x|
  
• 
  2) Чем дальше в лес, тем больше дров
  
• 
  3) Тише едешь, дальше будешь
  

Сообщение: Графики тригонометрических функций нашли применение во многих отраслях. Например, в области изобразительного искусства.

Как-то раз итальянский геометр Гвидо Гранди (1671-1742) создал розы. Нет, вовсе не те прекрасные растения, которые известны всем. Розы Гвидо Гранди радуют глаз правильными и плавными линиями, но их очертание не каприз природы – они предопределены математическими зависимостями.

Семейство роз Гвидо Гранди описывается графиком функции у = а*sin k , где а и k - некоторые числа. На рисунке изображены эти кривые при различных параметрах k. Очарованный результатами Гранди, немецкий геометр XIX в. Хабенихт также решил заняться математическим: «растениеводством». Хабенихт, путем многочисленных экспериментов «вырастил» замечательные экспонаты. А свои прекрасные цветы Гвидо Гранди собрал в одну книгу и назвал её «Цветник роз». В наши дни подобные эксперименты удобно проводить, имея под рукой персональный компьютер.

Тригонометрические функции также нашли применение в области физики. Давайте послушаем сообщение, приготовленное учащимся вашего класса. 

Графики можно складывать. На примере вы видите суммирующий зеленый график двух функций с одинаковым периодом.



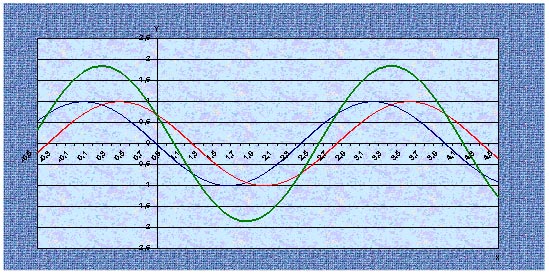
Сложение графиков можно наблюдать в природе. В физике это явление называется интерференцией.
Процедура сложения гармонических колебаний – не формальный математический прием. Она тесно связана с реальными физическими процессами, самыми распространенными из которых является звук и свет.
Своеобразие, прелесть и красота звуков различных голосов и музыкальных инструментов получается при сложении простых или “чистых” тонов, частоты колебаний которых относятся как 1 : 2 : 3 : 4 и т.д.
Наиболее низкий звук называется основным, а все остальные, более высокие тона называются высшими тонами или обертонами. “Чистый” тон графически изображается синусоидой, как и положено гармоническим колебаниям, а звук, например, трубы дает тоже периодический, но сложный по форме график, получаемый сложением различных тонов.

---

Сложение волн в пространстве называется интерференцией. Если звуки одинаковых частот наложить друг на друга, то амплитуда суммарных колебаний может как удвоиться, так и стать равной нулю. Все зависит от того складываются ли волны без разности фаз или в противофазе.
Не надо обладать музыкальным слухом, чтобы заметить, как изменится тон, высота звука, гудка локомотива, когда встречный поезд проносится мимо вас. Пока оба поезда сближаются, тон был намного выше, чем после встречи, когда поезда начали удаляться друг от друга. Отчего же это происходит? Гудок встречного локомотива издает все время один и тот же звук вполне определенной частоты. Но ухо воспринимает различное число колебаний в секунду, в зависимости от того, двигаетесь ли вы навстречу гудку или удаляетесь от него. Двигаясь навстречу, человек за секунду улавливаете больше колебаний, так как источник звука сам движется навстречу. Звук кажется выше. И все происходит наоборот, если вы удаляетесь от источника – тогда звук кажется ниже по тону.
Такой эффект кажущегося изменения частоты называется эффектом Доплера, по имени австрийского физика Кристиана Доплера (1803–1853).
Изменение частоты у световых волн приводит к изменению цвета - чем выше частота, тем ближе к фиолетовому и дальше от красного будет цвет. Стало быть, при движении навстречу источнику света, красный цвет изменится на желтый, а, возможно, на зеленый, синий и фиолетовый. Анекдотичный случай произошел с американским физиком-экспериментатором Робертом Вудом (1868–1955). Однажды полицейский остановил автомобиль Вуда за езду на красный цвет. Вуд, пытаясь оправдаться, рассказал полицейскому, что при движении навстречу источнику красного цвета из-за эффекта Доплера этот цвет вполне мог показаться ему зеленым. Но полицейский все-таки оштрафовал Вуда, не за езду на красный свет, а за превышение скорости. Еще бы – для того, чтобы принять красный свет за зеленый, Вуд должен был мчаться навстречу светофору с фантастической скоростью в 135 млн км/ч. Но шутка – шуткой, а именно эффект Доплера позволил ученым сделать вывод о расширении Вселенной, и о том, что когда-то она была “сжата в точку”.

Функция.

Прочтите наоборот.

1)Что кружится, что ложится
И на землю, и на крыши
И о чем поэт зимою
По ночам поэмы пишет?
Это первое словечко.

2) А второе просто "на"

3) Ну, а третье? Угадайте,
Что бежит по проводам?
Напиши, что получилось

---

И прочти наоборот
Не запутайся, читая,
Слово задом наперед.
(снег на ток - котангенс)

1)Привычное слово кудлатой наседки
Поставьте на первое место:

2) На месте втором посмотрите-ка - нота.
Важна для любого оркестра

3) На третьем одна одинокая буква,
пятнадцатая в алфавите

4) Один из волос на мордашке котенка
На месте четвертом прочтите.

Ответ: косинус.

Рожденный пустыней колеблется звук.
Колеблется синий на нитке паук.
Колеблется воздух, прозрачен и чист.
В сияющих звездах колеблется, лист.

Теперь выясним, кто станет председателем акционерного общества. Напоминаю: одна акция красного цвета равна трем акциям синего.

Идет подсчет количества акций и затем объявляется результат.

– Поздравляем председателя. Аукцион окончен. Имение графини продано!

8. Рефлексия (цветовая)

Постройте график функции у=2cosx одним из следующих  цветов, которые на ваш взгляд соответствуют вашему настроению от проделанной вами работы
Красный - отличное
Зеленый - хорошее
Синий – удовлетворительное

О какой кривой идёт речь?

Как утомительны вечные спуски,
Как утомительны вечные взлёты!...
В каждой ложбинке,
На каждой вершине –
Тщетна надежда – мечта о привале,
Об остановке и передышке. (синусоида)

9. Подведение итогов. Д/з.

Выставление оценок.

Повторить п.17-19, решить № 3(3), 4(3), 7(3), 8(4).

Презентация «Из истории тригонометрии».
Тема: Контрольная работа по теме «Свойства тригонометрических функций»

Цель:

• 
  Проверить уровень усвоения данной темы и уровень умений и навыков, сформированный по данной теме.
  
• 
  Развитие самоконтроля и самопроверки.
  
• 
  Воспитание трудолюбия и ответственности за выполнение работы.
  

Ход урока.

1.Организационный этап.

2.Постановка темы и цели урока.

3.Условие контрольной работы.

4.Итоги урока. Домашнее задание.0>

---

Смотрите также файлы

• Рассчитаем срок между приобретением и датой погашения.docx

• Суммативное оценивание за раздел 4 а Химические элементы и соединения в организме человека.docx

• I ii iii iv iii ii i.doc

• Курсовая работа 1 по дисциплине Теоретические основы электротехники.docx

• По Л. Н. Толстому.docx