Файл: Лекция 22. Тема урока Радианная мера углов. Цели урока 1 учебные.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 63
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Это позволяет построить график синуса на отрезке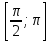 
. Воспользовавшись нечетностью синуса. Получим график синуса на отрезке 
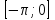симметричным отображением построенной части синусоиды относительно начала координат. Так как на отрезке 
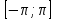имеет длину, равную периоду синуса, то график синуса на всей числовой оси можно получить параллельным переносами построенной кривой.
Затем учащиеся учатся изображать эскиз графика функции у = sin x по точкам и обобщают свойства функции.
На этом этапе учащимся выдаются опорные конспекты (все свойства заносятся в таблицу).
Построение графика функции на отрезке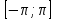
Значения синуса положительны (то есть ордината соответствующей точки единичной окружности положительна) в 1 и 11 четвертях. Таким образом, sin х>0 на отрезке (2πk; π+2πk), при k
.
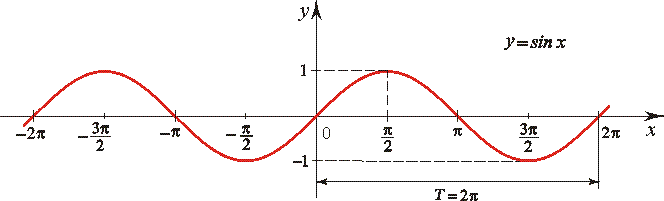График функции у = sinx построен.
Промежутки знакопостоянства.
Значения синуса положительны в 1 и 11 четвертях. Таким образом, sin x>0 на отрезке (2 πk ; π+2πk) k .
Промежутки знакопостоянства. Значения синуса отрицательны в 111 и 1V четвертях. Таким образом, sin x>0 на отрезке (π+2 πk ; 2π+2πk) k .
Если х 
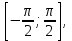то при увеличении аргумента х ордината соответствующей точки единичной окружности увеличивается. Следовательно , на этом промежутке функция sin xвозрастает.Если х 
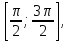то при увеличении аргумента х ордината соответствующей точки единичной окружности уменьшается. Следовательно, на этом промежутке функция
sin xубывает.
5. Закрепление первичных знаний.
С помощью таблицы и графика функции у = sin x отвечают на теоретические вопросы
Вместе с классом решаются задачи на сравнение;
А) Сравнить числа
sin 2 и sin 3 ; sin 1000 и sin 1300 ; sin 4и sin 2;
Расположить в порядке возрастания числа
sin 1.9; sin 3; sin(-1); sin(-1.5).
Решение
Числа sin 1.9 и sin 3 положительны, так как точки Р 1,9 и Р 3 находятся во 2 четверти. Функция у=sinх во 2 четверти убывает. sin 3 < sin 1.9
Числа sin(-1) и sin(-1.5) отрицательны, так как точка Р(-1) и Р(-1,5) находятся в 4 четверти.
Функция у=sinх во 4 четверти возрастает..
sin(-1.5) < sin(-1.5)
Ответ: Таким образом, в порядке возрастания эти числа располагаются так:
sin(-1.5); sin(-1); sin 3; sin 1.9.
6. Зарядка для коррекции зрения.
7. Самостоятельное работа.
Работа с таблицей. «Свойства функции у=соs x и ее график».
D(f)=
E(f)=
T=
Четность:
график симметричен относительно
f возрастает при х
f убывает при х
нули функции: х=
f>0 при х
f<0 при х
у наибольшее= при х=
у наименьшее= при х=
8. Преобразование графиков тригонометрических функций.
Сдвиг вдоль оси ординат.
Задача на построение графиков функций у=sinх+3 и у=sinх-3
Обсуждение свойств функции.
С
двиг вдоль оси абсцисс.
Задача на построение графиков функций у=sin(х - ) и у=соs(х+ )
Обсуждение свойств функции.
Сжатие и растяжение к оси абсцисс
Задача на построение графиков функций у= 3 sinх и у= 1/3 соsх
Обсуждение свойств функции.
С
жатие и растяжение к оси ординат
Задача на построение графиков функций у = sin2х и у = соs
Обсуждение свойств функции.
9, Историческая пауза об истории тригонометрии.
Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”.
Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum).
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру.
10. Выполнение упражнений на преобразование графиков тригонометрических функций. Решить 6(1), 7(1).
11. Подведение итогов. Рефлексия. Д/з.
Выставление оценок.
Н а уроке научились строить график функции у = sinx, у = соsx, читать свойства этого графика, строить эскиз графика, решать задачи связанные с использованием графика и свойств функции у = sinx, у = соsx.
Построить график функции у = sin2х+3 и у = sin(х- )
Описать свойства функций у = sinx, у = соsx. Выучить п.19, решить №1(1), 2(1), 5(1,2).
Тема урока: «Графики функций у=tg x и у=ctg x, их свойства»
Цели урока: Ознакомить учащихся со свойствами функции у=tg x и у=ctg x, обучение построению графика функции у=tg x и у=ctg x, чтению этого графика, использование свойств и графика функции у=tg x и у=ctg x, при решении неравенств.
Задачи урока.
Образовательные – формировать умение построения графика функции у=tg x и у=ctg x, рассмотреть свойства графика, формировать навыки свободного чтения графиков, умение считывать свойства функции по графику.
Развивающые – развивать логическое мышление, умение анализировать, обобщать полученные знания.
Воспитательные – активизировать интерес к получению новых знаний, воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.
Ход урока
1. Организационный момент. Приветствие. Эмоциональный настрой на урок.
2. Объявление темы и цели урока.
Тема урока: «Свойства функций у=tg x и у=ctg x и их графики».
Сегодня рассмотрим свойства функции у=tg x и у=ctg x и построим графики. Рассмотрим простейшие преобразования функции, построим графики этих функций и перечислим их свойства.
Из истории. Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников. В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников. Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.
Понятие таких тригонометрических функций, как тангенс, котангенс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном.
3 Актуализация опорных знаний:
Выполнение устных упражнений.
Повторить определение тригонометрических функций и знаки значений этих функций.
Затем учащиеся отвечают на вопросы:
Учащимся предложена иллюстрация единичной окружности.
Тригонометрия на руке. Работа с таблицей с.
если х = , х =
,
если х =
, х =
?
Самостоятельная работа
Вариант 1
№1. Вычислите: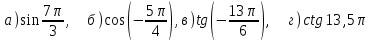
.
№2. Найдите заданную точку на числовой окружности: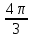
,
; -3,5; 240˚,180˚
№3. Вычислите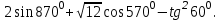
Вариант 2
№1. Вычислите: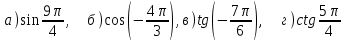
№2. Найдите заданную точку на числовой окружности: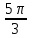
, 
; -1,5; 340˚,270˚
№3.Вычислите: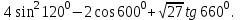
4. Изложение нового материала.
Что кружится, что ложится
И на землю, и на крыши,
И о чем поэт зимою
По ночам поэмы пишет?
Это первое словечко
А второе просто «на».
Ну, а третье? Угадайте,
Что бежит по проводам?
Напиши, что получилось,
И прочти наоборот.
Не запутайся, читая
Слово задом наперед!
(Снег-на-ток…котангенс)
Обобщение и конкретизация знаний, полученных ранее: 1)область определения, 2)множества значений, 3)четность или нечетность, 4) периодичность,5) точки пересечения с осями координат, 6) промежутки знакопостоянства, 7) промежутки возрастания и убывания, 8) наибольшее и наименьшее значение функции.
Выделенные характеристики позволят построить сначала часть графика функции у=tg x
1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = π/2 + πk, где k – любое целое число.
Это означает, что на графике функции нет точки, принадлежащей прямой x = π/2,
либо прямой x = 3π/2, либо прямой x = 5π/2, либо прямой x = –π/2 и т.д.
2) Область значений функции (–∞; +∞)
3) Это нечетная функция.
4) Это непрерывная функция на интервале (–π/2; π/2).
5) Это периодическая функция с основным периодом π (Т = π)
6) Функция возрастает на интервале (–π/2; π/2).
7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений.
Просмотр презентации.
Работа с учебником: Свойства и график функции у=ctg x.
1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = πk, где k – любое целое число.
2) Область значений функции (–∞; +∞)
3) Это нечетная функция.
4) Это непрерывная функция.
5) Это периодическая функция с основным периодом π (Т = π)
6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число.
7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений.
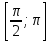. Воспользовавшись нечетностью синуса. Получим график синуса на отрезке 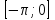симметричным отображением построенной части синусоиды относительно начала координат. Так как на отрезке 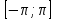имеет длину, равную периоду синуса, то график синуса на всей числовой оси можно получить параллельным переносами построенной кривой.Затем учащиеся учатся изображать эскиз графика функции у = sin x по точкам и обобщают свойства функции.
На этом этапе учащимся выдаются опорные конспекты (все свойства заносятся в таблицу).
Построение графика функции на отрезке
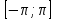
Значения синуса положительны (то есть ордината соответствующей точки единичной окружности положительна) в 1 и 11 четвертях. Таким образом, sin х>0 на отрезке (2πk; π+2πk), при k
. График функции у = sinx построен. Промежутки знакопостоянства.
Значения синуса положительны в 1 и 11 четвертях. Таким образом, sin x>0 на отрезке (2 πk ; π+2πk) k
.Промежутки знакопостоянства. Значения синуса отрицательны в 111 и 1V четвертях. Таким образом, sin x>0 на отрезке (π+2 πk ; 2π+2πk) k
.Если х
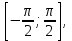то при увеличении аргумента х ордината соответствующей точки единичной окружности увеличивается. Следовательно , на этом промежутке функция sin xвозрастает.Если х 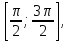то при увеличении аргумента х ордината соответствующей точки единичной окружности уменьшается. Следовательно, на этом промежутке функция
sin xубывает.
5. Закрепление первичных знаний.
С помощью таблицы и графика функции у = sin x отвечают на теоретические вопросы
Вместе с классом решаются задачи на сравнение;
А) Сравнить числа
sin 2 и sin 3 ; sin 1000 и sin 1300 ; sin 4и sin 2;
Расположить в порядке возрастания числа
sin 1.9; sin 3; sin(-1); sin(-1.5).
Решение
Числа sin 1.9 и sin 3 положительны, так как точки Р 1,9 и Р 3 находятся во 2 четверти. Функция у=sinх во 2 четверти убывает. sin 3 < sin 1.9
Числа sin(-1) и sin(-1.5) отрицательны, так как точка Р(-1) и Р(-1,5) находятся в 4 четверти.
Функция у=sinх во 4 четверти возрастает..
sin(-1.5) < sin(-1.5)
Ответ: Таким образом, в порядке возрастания эти числа располагаются так:
sin(-1.5); sin(-1); sin 3; sin 1.9.
6. Зарядка для коррекции зрения.
7. Самостоятельное работа.
Работа с таблицей. «Свойства функции у=соs x и ее график».
D(f)=
E(f)=
T=
Четность:
график симметричен относительно
f возрастает при х
f убывает при х
нули функции: х=
f>0 при х
f<0 при х
у наибольшее= при х=
у наименьшее= при х=
8. Преобразование графиков тригонометрических функций.
Сдвиг вдоль оси ординат.
Задача на построение графиков функций у=sinх+3 и у=sinх-3
Обсуждение свойств функции.
С
двиг вдоль оси абсцисс.Задача на построение графиков функций у=sin(х - ) и у=соs(х+ )
Обсуждение свойств функции.
Сжатие и растяжение к оси абсцисс
Задача на построение графиков функций у= 3 sinх и у= 1/3 соsх
Обсуждение свойств функции.
С
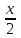жатие и растяжение к оси ординатЗадача на построение графиков функций у = sin2х и у = соs
Обсуждение свойств функции.
9, Историческая пауза об истории тригонометрии.
Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”.
Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum).
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру.
10. Выполнение упражнений на преобразование графиков тригонометрических функций. Решить 6(1), 7(1).
11. Подведение итогов. Рефлексия. Д/з.
Выставление оценок.
Н
а уроке научились строить график функции у = sinx, у = соsx, читать свойства этого графика, строить эскиз графика, решать задачи связанные с использованием графика и свойств функции у = sinx, у = соsx.Построить график функции у = sin2х+3 и у = sin(х- )
Описать свойства функций у = sinx, у = соsx. Выучить п.19, решить №1(1), 2(1), 5(1,2).
Тема урока: «Графики функций у=tg x и у=ctg x, их свойства»
Цели урока: Ознакомить учащихся со свойствами функции у=tg x и у=ctg x, обучение построению графика функции у=tg x и у=ctg x, чтению этого графика, использование свойств и графика функции у=tg x и у=ctg x, при решении неравенств.
Задачи урока.
Образовательные – формировать умение построения графика функции у=tg x и у=ctg x, рассмотреть свойства графика, формировать навыки свободного чтения графиков, умение считывать свойства функции по графику.
Развивающые – развивать логическое мышление, умение анализировать, обобщать полученные знания.
Воспитательные – активизировать интерес к получению новых знаний, воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.
Ход урока
1. Организационный момент. Приветствие. Эмоциональный настрой на урок.
2. Объявление темы и цели урока.
Тема урока: «Свойства функций у=tg x и у=ctg x и их графики».
Сегодня рассмотрим свойства функции у=tg x и у=ctg x и построим графики. Рассмотрим простейшие преобразования функции, построим графики этих функций и перечислим их свойства.
Из истории. Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников. В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников. Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.
Понятие таких тригонометрических функций, как тангенс, котангенс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном.
3 Актуализация опорных знаний:
Выполнение устных упражнений.
Повторить определение тригонометрических функций и знаки значений этих функций.
Затем учащиеся отвечают на вопросы:
Учащимся предложена иллюстрация единичной окружности.
Тригонометрия на руке. Работа с таблицей с.
-
Какой знак имеет значение функции у = tg x?
если х =
, х = , если х =
, х = ?Самостоятельная работа
Вариант 1
№1. Вычислите:
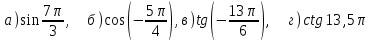.№2. Найдите заданную точку на числовой окружности:
,
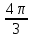
; -3,5; 240˚,180˚№3. Вычислите
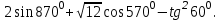
Вариант 2
№1. Вычислите:
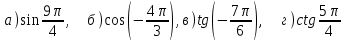
№2. Найдите заданную точку на числовой окружности:
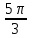, ; -1,5; 340˚,270˚№3.Вычислите:
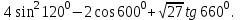
4. Изложение нового материала.
Что кружится, что ложится
И на землю, и на крыши,
И о чем поэт зимою
По ночам поэмы пишет?
Это первое словечко
А второе просто «на».
Ну, а третье? Угадайте,
Что бежит по проводам?
Напиши, что получилось,
И прочти наоборот.
Не запутайся, читая
Слово задом наперед!
(Снег-на-ток…котангенс)
Обобщение и конкретизация знаний, полученных ранее: 1)область определения, 2)множества значений, 3)четность или нечетность, 4) периодичность,5) точки пересечения с осями координат, 6) промежутки знакопостоянства, 7) промежутки возрастания и убывания, 8) наибольшее и наименьшее значение функции.
Выделенные характеристики позволят построить сначала часть графика функции у=tg x
1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = π/2 + πk, где k – любое целое число.
Это означает, что на графике функции нет точки, принадлежащей прямой x = π/2,
либо прямой x = 3π/2, либо прямой x = 5π/2, либо прямой x = –π/2 и т.д.
2) Область значений функции (–∞; +∞)
3) Это нечетная функция.
4) Это непрерывная функция на интервале (–π/2; π/2).
5) Это периодическая функция с основным периодом π (Т = π)
6) Функция возрастает на интервале (–π/2; π/2).
7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений.
Просмотр презентации.
Работа с учебником: Свойства и график функции у=ctg x.
1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = πk, где k – любое целое число.
2) Область значений функции (–∞; +∞)
3) Это нечетная функция.
4) Это непрерывная функция.
5) Это периодическая функция с основным периодом π (Т = π)
6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число.
7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений.