Файл: 1. Кристаллическое состояние вещества. Признаки и основные свойства кристаллов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 41
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Кристаллическое состояние вещества. Признаки и основные свойства кристаллов.
Кристаллическое состояние вещества характеризуется наличием дальнего порядка в расположении частиц (атомов, молекул, ионов), т.е. внутреннее упорядоченное строение.
Твёрдое тело представляет собой кристалл или кристаллическое вещество, если при прохождении через него рентгеновских лучей происходит дифракция и видна ясная дифракционная картина.
Основные свойства кристаллов:
1) Однородность – любые элементарные объёмы кристаллического вещества, одинаково ориентированные в пространстве, абсолютно одинаковы по всем физическим свойствам.
2) Анизотропность – физические свойства не одинаковы по не параллельным направлениям.
3) Самоогранение – любой обломок кристалла в соответствующей для его роста среде с течением времени покрывается характерными для данных кристаллов гранями.
2. Элементы симметрии кристаллических многогранников.
Элементы симметрии – воображаемые геометрические образы, под действием которых повторяются части симметричных фигур.
Элементы симметрии:
1) Центр инверсии (симметрии) – особая точка внутри фигуры, совпадающая с центром тяжести многогранника (C)
2) Поворотная ось (ось симметрии) – прямая линия, вокруг которой закономерно повторяются равные части фигур (Ln)
!) Инверсионные оси – сочетание поворота вокруг оси вращения с отражением в центре симметрии
Li1 = C
Li2 = P
Li3 = L3C
Li4 = L2
Li6 = L3P (P перпендикулярна L3)
3) Плоскость зеркального отражения – делит фигуру на 2 зеркальные равные части
Все элементы симметрии всегда проходят через центр тяжести многогранника (P)
3. Теоремы сложения элементов симметрии.
Теорема Эйлера: если существуют 2 элемента симметрии, то обязательно присутствует третий, равнодействующий для первых двух.
Т1: линия пересечения двух плоскостей – простая ось симметрии
Следствие 1: если через ось симметрии проходит плоскость, то число проходящих через ось, равно порядку оси
Т2: ось чётного порядка + центр симметрии = перпендикулярная плоскость
Следствие 2: если есть центр симметрии, то сумма чётных осей = сумме плоскостей отражения
Т3: две пересекающиеся оси дают третью равнодействующую ось, проходящую через точку их пересечения
4. Закон Стенона-Роме-Делиля. Гониометрический метод изучения формы кристаллов.
Закон постоянства углов гласит, что углы между соответственными гранями и ребрами кристаллов одного и того же вещества постоянны
Гониометрический метод:
Основан на законе постоянства углов между соответствующими гранями. Для измерения углов используют прикладные и отражательные гониометры.
5. Сингонии. Характеристика сингоний по единичным направлениям.
Сингония – группа видов симметрии с одним или несколькими сходными элементами симметрии.
Низшая категория:
Триклинная сингония – все направления единичные
Моноклиннная сингония – много, но не все направления единичные
Ромбическая сингония – три единичных направления
Средняя категория (тригональная, тетрагональная и гексагональная сингонии):
Одно единичное направление, совпадает с главной осью
Высшая категория (кубическая сингония):
Нет единичных направлений
6. Вывод видов симметрии низшей категории.
Триклинная сингония: Примитивный – [ - (1)] Минимальный набор поворотных осей
Добавляем центр – Центральный [Li1 = C (
 )] Поворотные оси + центр (здесь Li1)
)] Поворотные оси + центр (здесь Li1)Моноклинная: Аксиальный – только L2 (2) Главная ось + | L2
Планальный – только P (m) Плоскости симметрии + поворотная ось
Планаксиальный – L2 + C = P –> L2PC Аксиальный + центр
Ромбическая: Аксиальный – 3L2 (222) Главная ось + | L2
Планальный – P + P = L2 (линия пересечения двух плоскостей – простая ось симметрии) –> L22P (mm2) Плоскости симметрии + поворотная ось
Планаксиальный – к 3L2 добавим центр –> 3L23PC Аксиальный + центр
7. Вывод видов симметрии тетрагональной сингонии.
Примитивный – только L4 (4) Минимальный набор поворотных осей
Центральный – L4 + C = P –> L4PC Поворотные оси + центр
Аксиальный – L44L2 Главная ось + | L2
Планальный – L44P Плоскости симметрии + поворотная ось
Планаксиальный – L44L25PC Аксиальный + центр
Инверсионно-примитивный – Li4 Только инверсионная ось
Инверсионно-планальный – Li43L22P Инверсионно-примитивный + плоскость (Li4 = L2)
8. Вывод видов симметрии гексагональной сингонии.
Примитивный – только L6 (6) Минимальный набор поворотных осей
Центральный – L6 + C = P –> L6PC Поворотные оси + центр
Аксиальный – L66L2 Главная ось + | L2
Планальный – L66P Плоскости симметрии + поворотная ось
Планаксиальный – L66L27PC Аксиальный + центр
Инверсионно-примитивный – Li6 Только инверсионная ось
Инверсионно-планальный – Li63L23P Инверсионно-примитивный + плоскость (Li6 = L3P)
9. Вывод видов симметрии кубической сингонии.
Примитивный – 4L33L2 Минимальный набор поворотных осей
Центральный – 4L33L2 + C = 4L33L23PC Поворотные оси + центр
Аксиальный – 3L44L36L2 Главная ось + | L2
Планальный – 4L33L26P = 3Li44L36P Плоскости симметрии + поворотная ось (Li4 = L2)
Планаксиальный – 3L44L36L29PC Аксиальный + центр
10. Кристаллографические (стереографические) проекции элементов симметрии кристаллов.
Те самые штуки, которые мы рисуем на проекциях

Проекция вертикальной оси симметрии попадет в центр круга проекции.
Проекции горизонтальных осей симметрии являются диаметрами круга проекции
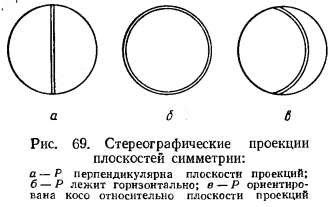
Проекция вертикальной плоскости симметрии является диаметром круга
Проекция горизонтальной плоскости симметрии совпадает с кругом проекции
11. Кристаллографические (гномостереографические) проекции граней кристаллов.
Эммм…. Крестик и нолик?
12. Простые формы кристаллов и комбинационные многогранники.
Форма многогранника – совокупность всех его граней
Простая форма – совокупность всех граней многогранника, которые связаны между собой элементами симметрии
Закрытая простая форма – совокупность граней, полностью замыкающих заключённое между ними пространство. Открытая форма, соответственно, не замыкает. Открытые формы встречаются только в низшей и средней категории.
Комбинационные многогранники – многогранники, содержащие грани нескольких простых форм
13. Простые формы низшей категории.
Моноэдр, Пинакоид, Диэдр, Ромбическая призма, Ромбическая пирамида, Ромбическая дипирамида, Ромбический тетраэдр
14. Простые формы тригональной сингонии.
Тригональная (+ Дитригональная ) призма, Тригональная (+Дитригональная) пирамида, Тригональная (+Дитригональная) дипирамида, Ромбоэдр, Тригональный скаленоэдр, Тригональный трапецоэдр
15. Простые формы тетрагональной сингонии.
Тетрагональная (+ Дитетрагональная ) призма, Тетрагональная (+ Дитетрагональная ) пирамида, Тетрагональная (+ Дитетрагональная ) дипирамида, Тетрагональный тетраэдр, Тетрагональный скаленоэдр, Тетрагональный трапецоэдр
16. Простые формы гексагональной сингонии.
Гексагональная (+ Дигексагональная ) призма, Гексагональная (+ Дигексагональная ) пирамида, Гексагональная (+ Дигексагональная ) дипирамида, Гексагональный трапецоэдр
17. Простые формы общего положения в кубической сингонии.
Пентагонтритетраэдр, Гексатетраэдр, Дидодекаэдр, Пентагонтриоктаэдр, Гексаоктаэдр
18. Частные простые формы кристаллов кубической сингонии – производные куба.
Тетрагексаэдр, Ромбододэкаэдр, Пентагондодекаэдр
19. Частные простые формы кристаллов кубической сингонии – производные октаэдра и тетраэдра.
Тригонтритетраэдр, Тетрагонтритетраэдр, Тригонтриоктаэдр, Тетрагонтриоктаэдр
20. Разновидности простых форм. Энантиоморфизм.
Закрытая простая форма – совокупность граней, полностью замыкающих заключённое между ними пространство. Открытая форма, соответственно, не замыкает. Открытые формы встречаются только в низшей и средней категории.
Грань частного положения фиксирована какими-либо элементами симметрии (перпендикулярно, параллельно или равнонаклонно). Остальные положения граней – общие, т. е. не зафиксированные относительно элементов симметрии.
Разновидности простых форм? Вершинные и рёберные?
Энантиоморфизм -- Свойство некоторых кристаллов существовать в модификациях, являющихся зеркальными отражениями друг друга
21. Кристаллографические системы координат. Установка кристаллов низшей категории, выбор единичной грани.
Кристаллографическая система координат. В общем случае косоугольная, начало координат в узле пространственной решетки, оси совпадают с рядами узлов решетки. При наличии элементов симметрии оси выбираются по осям симметрии или по нормалям к плоскостям симметрии
Установка:
1. Центр тяжести кристалла совмещается с центром круга проекции
2. Кристаллы триклинной сингонии устанавливаются так, чтобы наибольшее число граней располагалось вертикально
3. Кристаллы моноклинной сингонии устанавливаются так, чтобы ось 2-го порядка располагалась горизонтально, а наибольшее число граней располагалось вертикально
4. Кристаллы ромбической сингонии устанавливаются так, чтобы одна из осей 2-го порядка располагалась вертикально
Триклинная сингония — оси x,y,z вдоль ребер кристалла, ось z вдоль наиболее развитой зоны граней, углы между осями близки к 90о
Моноклинная сингония — Ось y вдоль оси 2-го порядка или перпендикулярна к плоскости (слева направо), оси z вертикально параллельно ребрам наиболее развитой зоны, ось х параллельно ребру, направлена на наблюдателя
Ромбическая сингония — Оси х y z — единичные направления вдоль осей 2-го порядка или перпендикулярно плоскостям симметрии
Единичная грань пересекает все оси, или две двуединичные грани пересекают по две оси
22. Кристаллографические системы координат. Установка кристаллов тригональной и гексагональной сингоний, выбор единичной грани.
Установка: Кристаллы средней категории устанавливаются так, чтобы ось высшего порядка располагалась вертикально
Тригональная и гексагональная сингонии — Ось z вдоль главной оси 3-го или 6-го порядка Оси х, y, j — вдоль осей 2-го порядка или перпендикулярно плоскостям симметрии; Углы между горизонтальными осями 120о
Единичная грань: та, которая пересекает все три оси или хотя бы две
23. Кристаллографические системы координат. Установка кристаллов тетрагональной и кубической сингоний, выбор единичной грани.
Установка: Кристаллы кубической сингонии устанавливаются так, чтобы одна из осей 4-го или 2-го порядка располагалась вертикально
Тетрагональная сингония — Ось z вдоль оси 4-го порядка Оси х y — вдоль осей 2-го порядка или перпендикулярно плоскостям симметрии; Оси взаимно перпендикулярны (ортогональная установка)
Кубическая сингония — Оси х y z — по осям 4-го или 2-го порядка, оси взаимно перпендикулярны (ортогональная установка)
Единичная грань: октаэдра или тетраэдра, даже если их нет в реальном кристалле
24. Обозначения видов симметрии по Браве и Герману-Могену.
Поворотные оси симметрии обозначаются арабскими цифрами, соответствующими порядку оси: L