ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 126
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
— набор этих переменных. Введем обозначение: 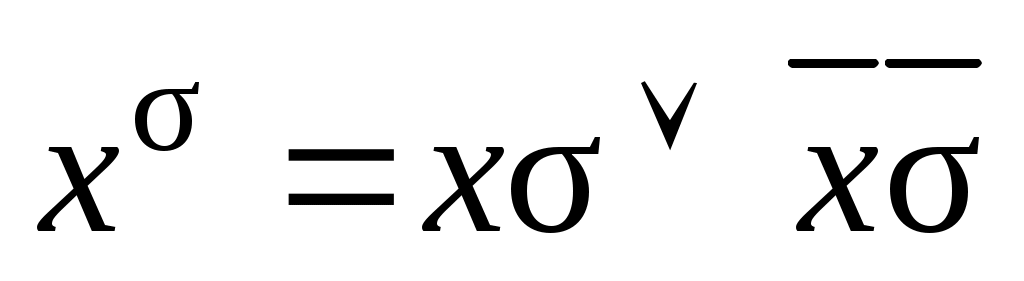 , где
, где 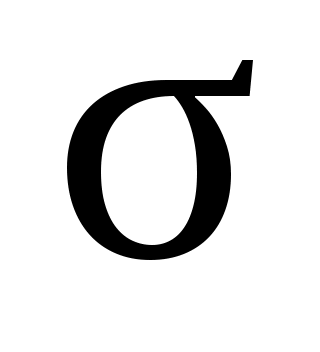 — параметр, равный 0 или 1. Очевидно, что
— параметр, равный 0 или 1. Очевидно, что 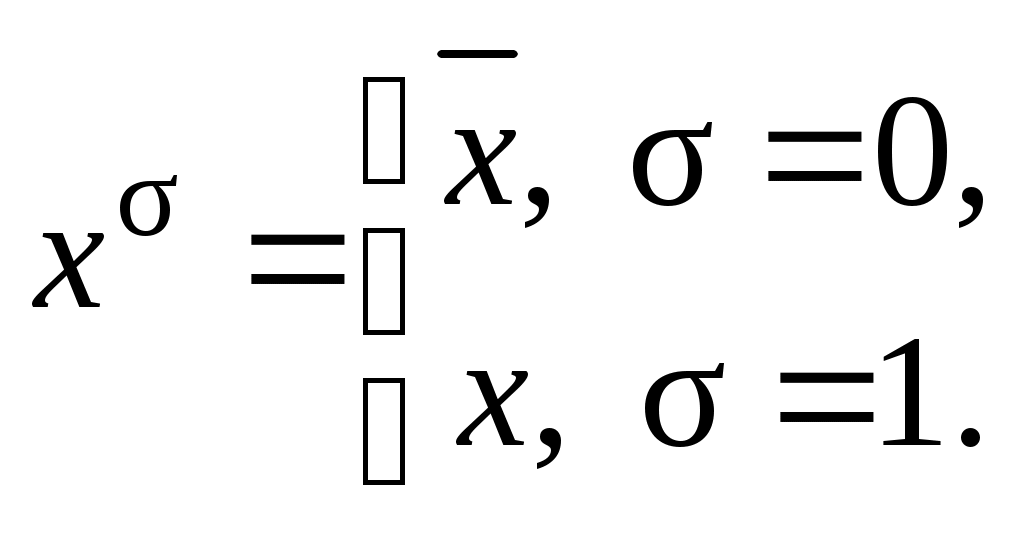 Тогда функцию
Тогда функцию  можно представить в виде:
можно представить в виде:
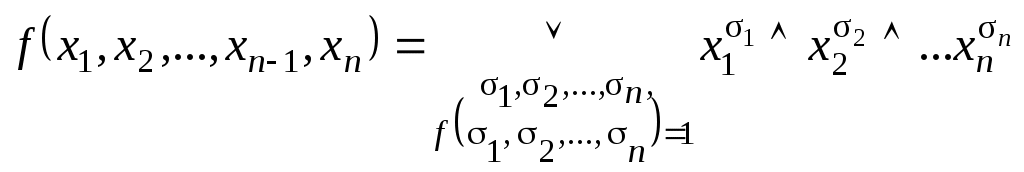 , (1.13.4)
, (1.13.4)
где дизъюнкция берется по всевозможным наборам значений переменных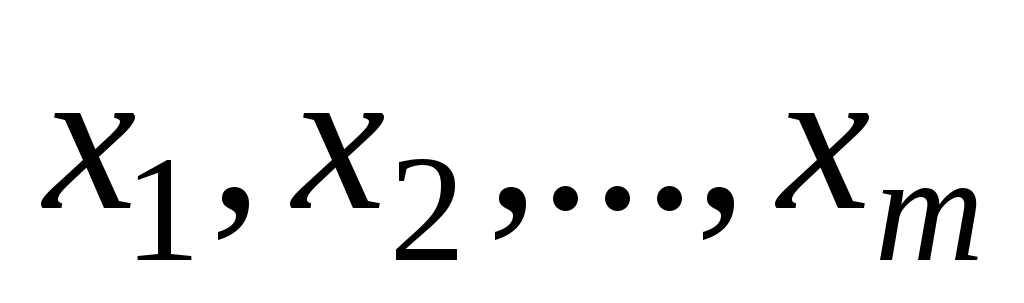 или
или
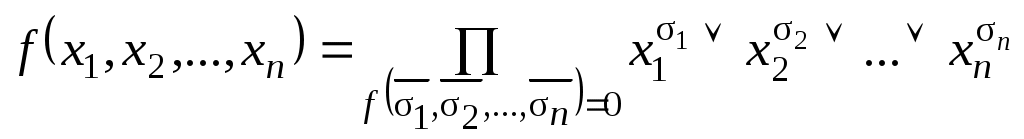 , (1.13.5)
, (1.13.5)
где символ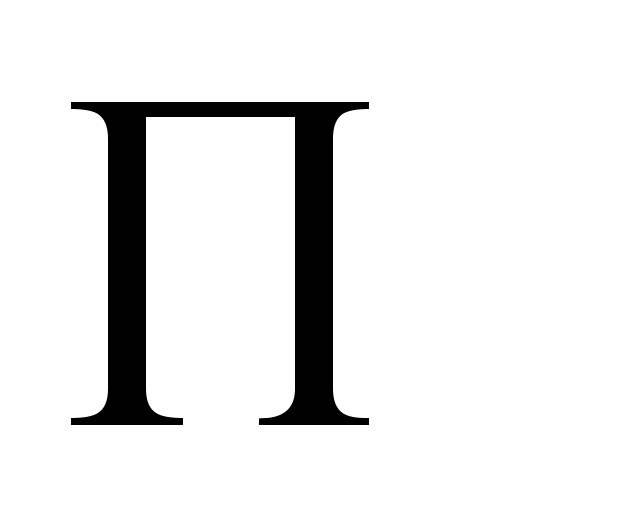 означает, что конъюнкции берутся по тем наборам переменных, которые указаны под ним. Нормальные формы позволяют дать критерий равносильности двух произвольных формул
означает, что конъюнкции берутся по тем наборам переменных, которые указаны под ним. Нормальные формы позволяют дать критерий равносильности двух произвольных формул  и
и  .
.
Аппарат булевых функций используется для проектирования цифровых устройств и базовых элементов компьютерных систем.
Первичным понятием теории множеств является понятие самого множества. Множество — это совокупность некоторых (произвольных) объектов, объединенных по какому-либо признаку. Элементы множества при этом должны быть различными. Множество обозначается парой скобок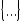 , внутри которых либо просто перечисляются элементы, либо описываются их свойства. Например,
, внутри которых либо просто перечисляются элементы, либо описываются их свойства. Например, 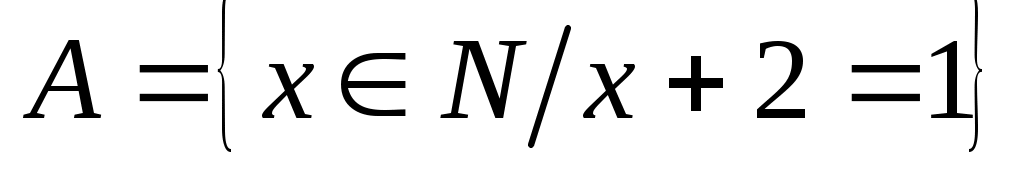 — множество натуральных чисел, удовлетворяющих условию
— множество натуральных чисел, удовлетворяющих условию 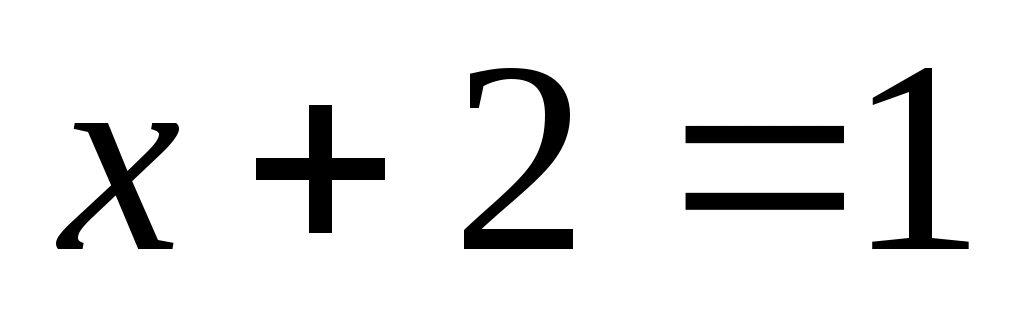 , очевидно, пусто.
, очевидно, пусто. 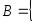 сложение, умножение
сложение, умножение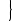 — множество основных арифметических операций. Пустое множество обозначается знаком . Если необходимо указать, что объект
— множество основных арифметических операций. Пустое множество обозначается знаком . Если необходимо указать, что объект  является элементом множества
является элементом множества  , то пишут
, то пишут  (
( принадлежит
принадлежит  ), наоборот запись
), наоборот запись 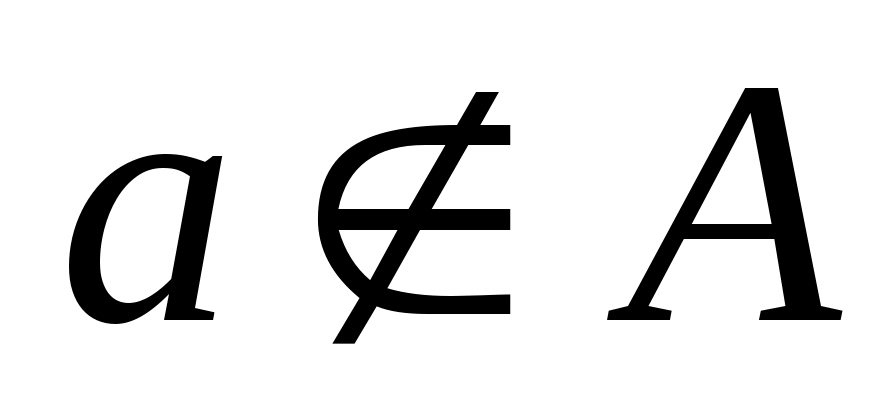 говорит о том, что
говорит о том, что  не принадлежит
не принадлежит 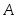 .
.
Если каждый элемент множества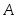 является элементом множества
является элементом множества 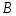 , то пишут
, то пишут 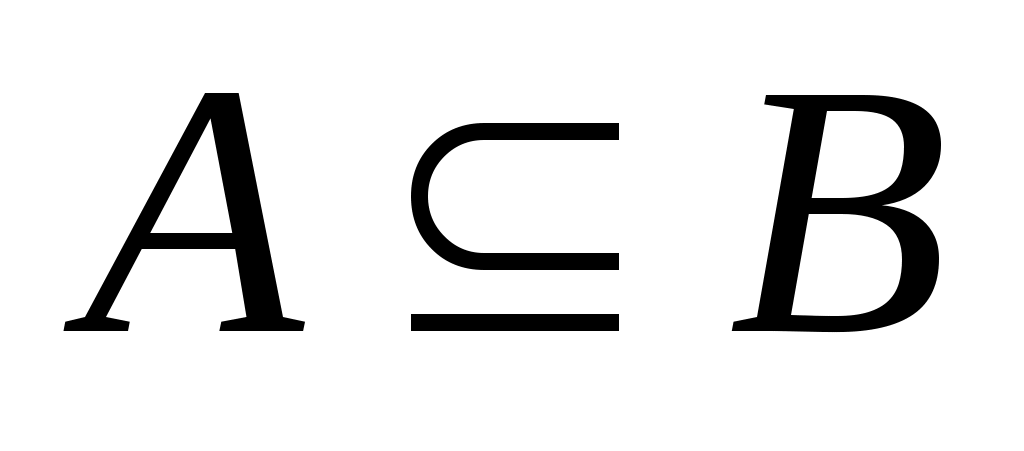 или
или 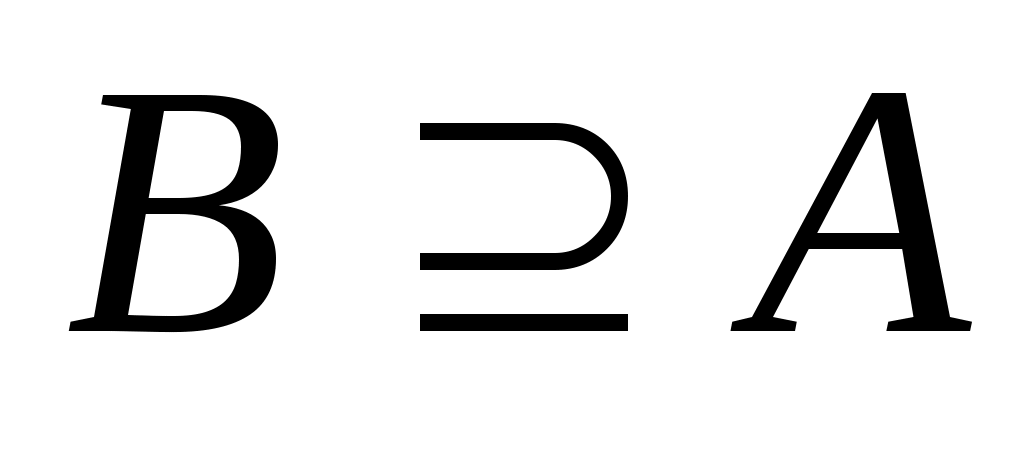 и говорят, что множество
и говорят, что множество 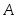
является подмножеством множества . Если
. Если  есть подмножество множества
есть подмножество множества 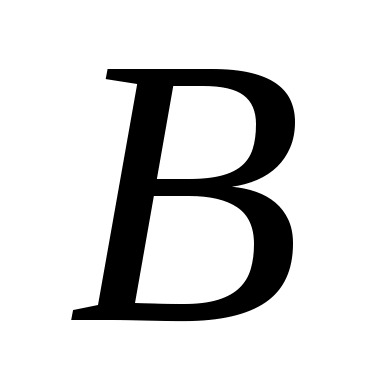 , причем
, причем 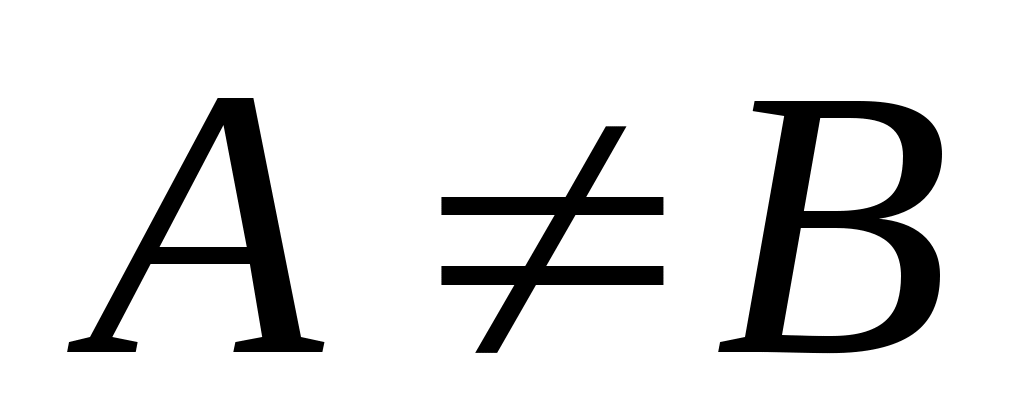 , то пишут
, то пишут 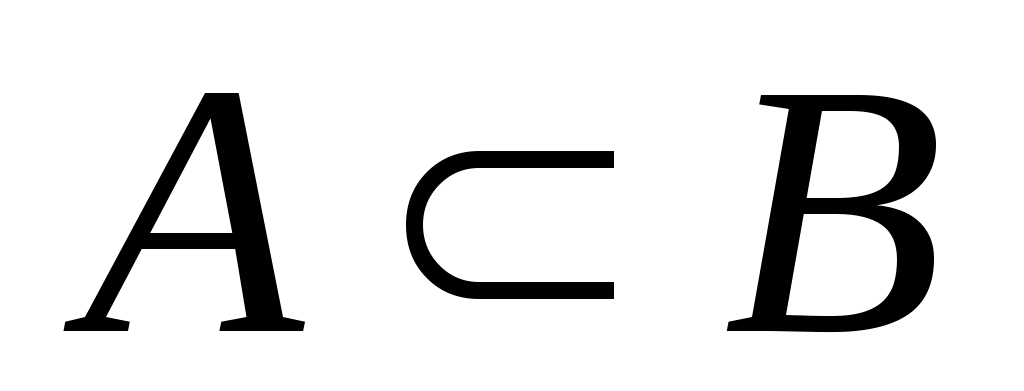 или
или 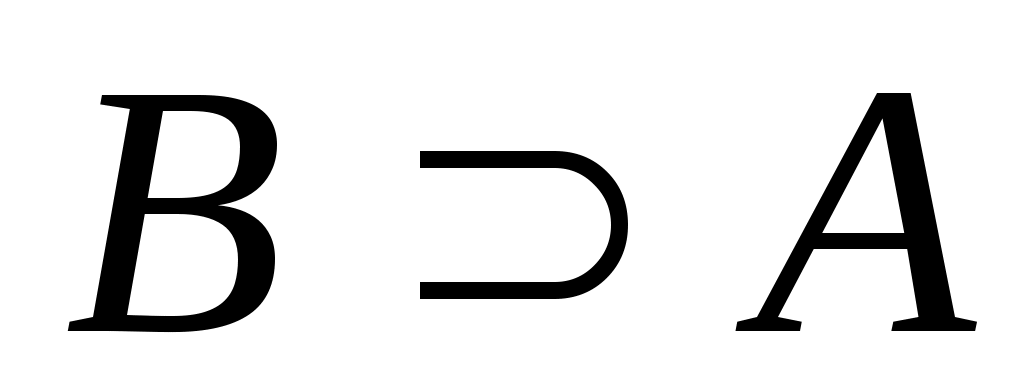 . Множества, состоящие из одних и тех же элементов, называются равными, то есть
. Множества, состоящие из одних и тех же элементов, называются равными, то есть 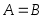 , в противном случае
, в противном случае 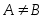 . С помощью скобок и операций над множествами можно построить новые множества, более сложные, чем исходные.
. С помощью скобок и операций над множествами можно построить новые множества, более сложные, чем исходные.
Объединение (или сумма). Эта операция над множествами обозначается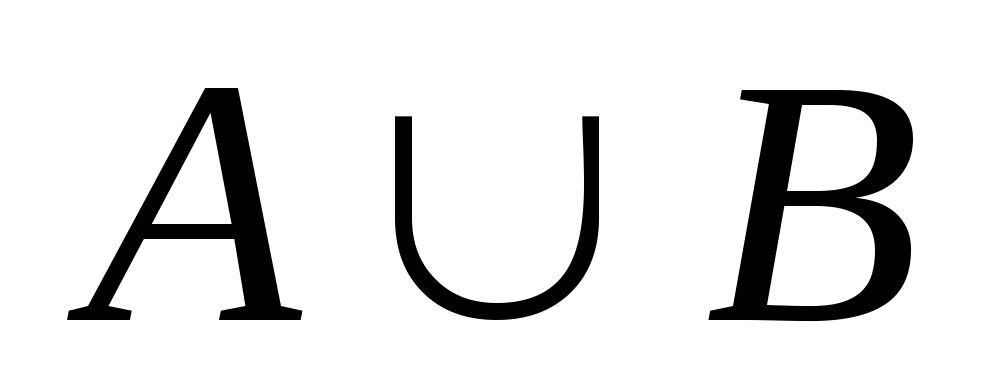 , определяется как
, определяется как 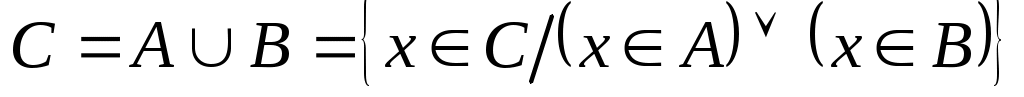 . Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера5- Венна6. Если за некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить
. Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера5- Венна6. Если за некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить 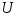 (или
(или 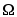 ) и изобразить его в виде всей плоскости, то любое множество
) и изобразить его в виде всей плоскости, то любое множество 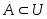 можно изобразить в виде части плоскости, то есть в виде некоторой фигуры, лежащей на плоскости. Множество
можно изобразить в виде части плоскости, то есть в виде некоторой фигуры, лежащей на плоскости. Множество  объединение множеств
объединение множеств  и
и  ,
,  на рис. 1.7 заштриховано.
на рис. 1.7 заштриховано. 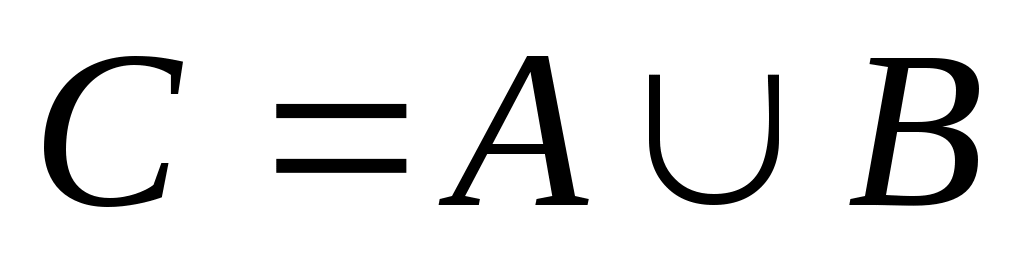 .
.
Р
ис. 1.7.
Объединение множеств
Рис. 1.8. Пересечение множеств
Пересечением (или произведением) двух множеств называется такое множество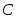 , которое состоит из элементов, принадлежащим одновременно обоим множествам, то есть
, которое состоит из элементов, принадлежащим одновременно обоим множествам, то есть 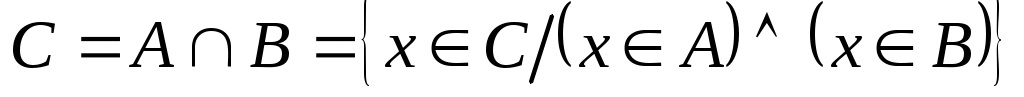 . Пересечение множеств
. Пересечение множеств  и
и  заштриховано и изображено на рис. 1.8.
заштриховано и изображено на рис. 1.8.
Разностью двух множеств и
и  называется множество
называется множество 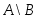 , состоящее из тех и только тех элементов, которые входят в
, состоящее из тех и только тех элементов, которые входят в  и одновременно не входят в
и одновременно не входят в  , то есть
, то есть 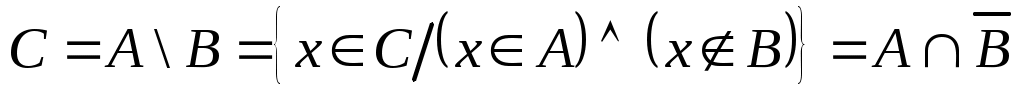 (рис. 1.9). Если, в частности,
(рис. 1.9). Если, в частности,  подмножество
подмножество  , то разность
, то разность 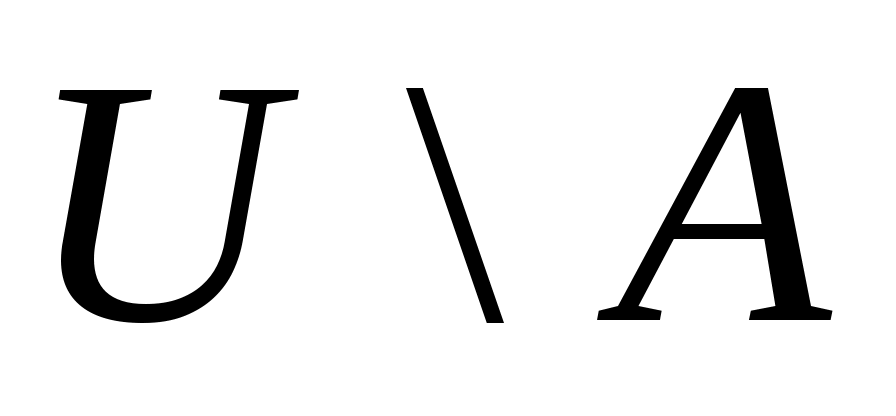 обозначается
обозначается 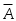 и называется дополнением множества
и называется дополнением множества  (рис. 1.10).
(рис. 1.10).
Рис. 1.9. Разность множеств
Рис. 1.10. Дополнение множества
С
имметрической разностью или кольцевой суммой множеств и
и  называется множество
называется множество 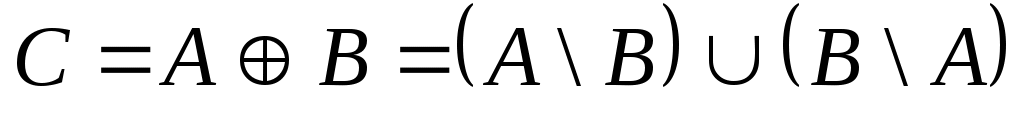 (рис. 1.11). Очевидно, что
(рис. 1.11). Очевидно, что 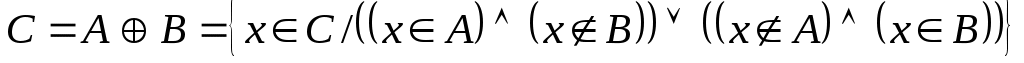
. Если и
и 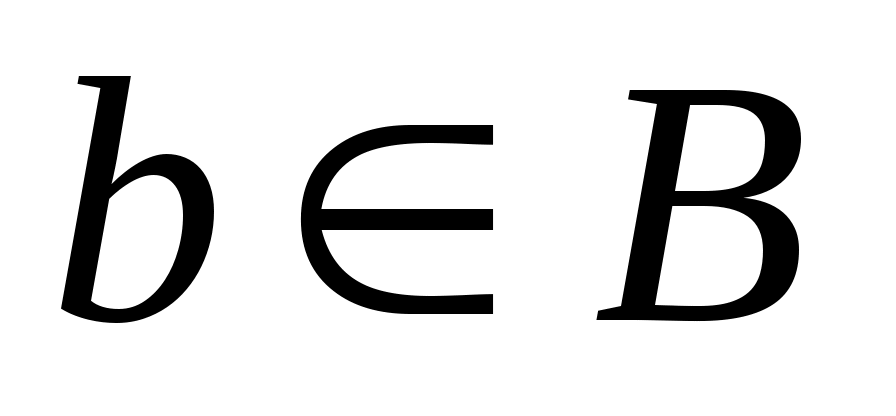 , то пару элементов
, то пару элементов 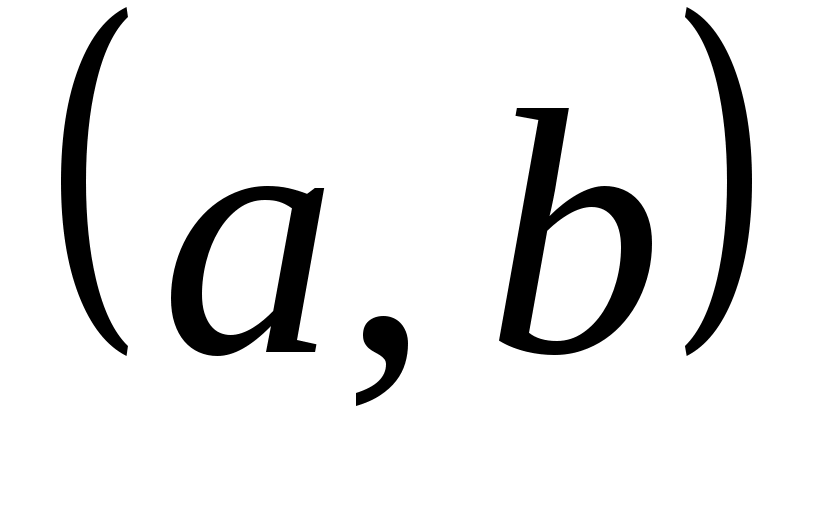 называют упорядоченной парой, причем пары
называют упорядоченной парой, причем пары 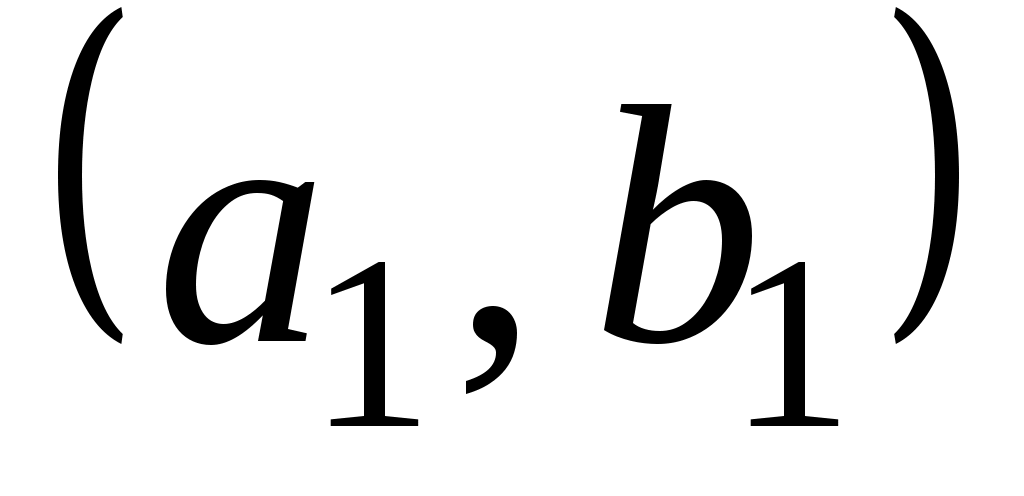 и
и 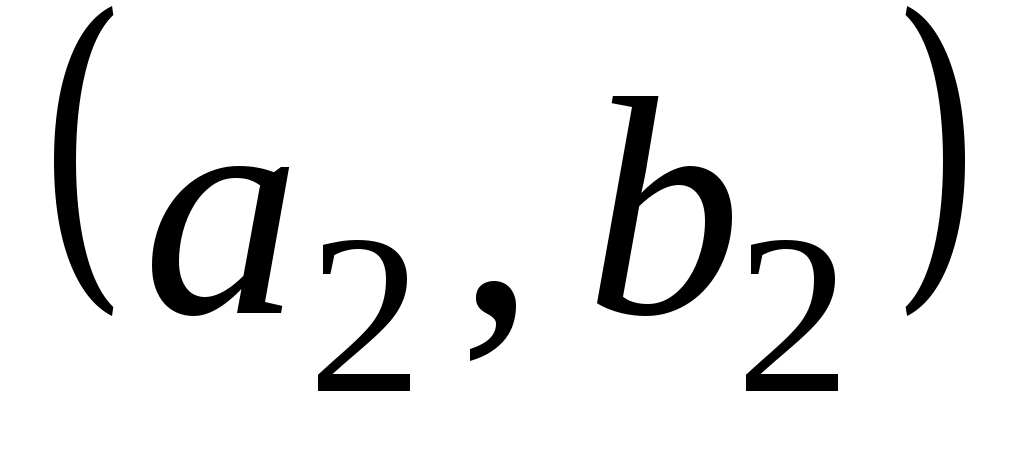 равны тогда и только тогда, когда
равны тогда и только тогда, когда 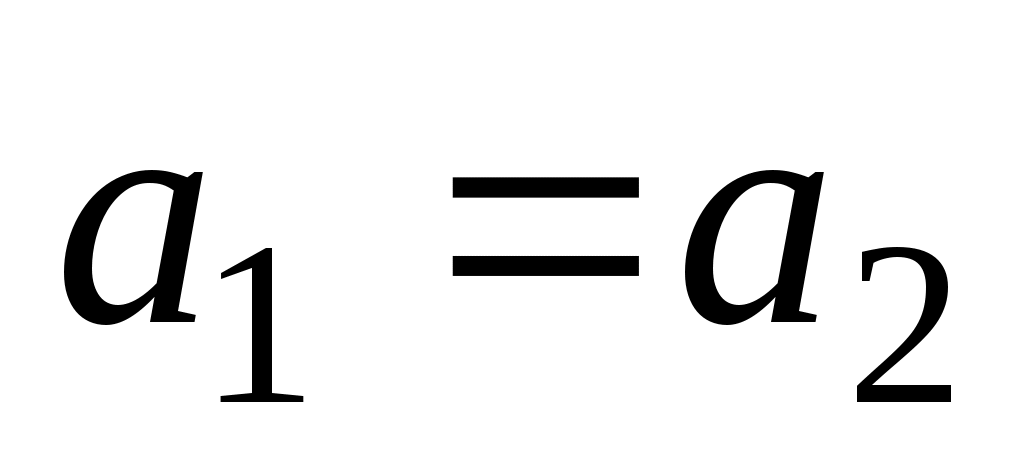 и
и 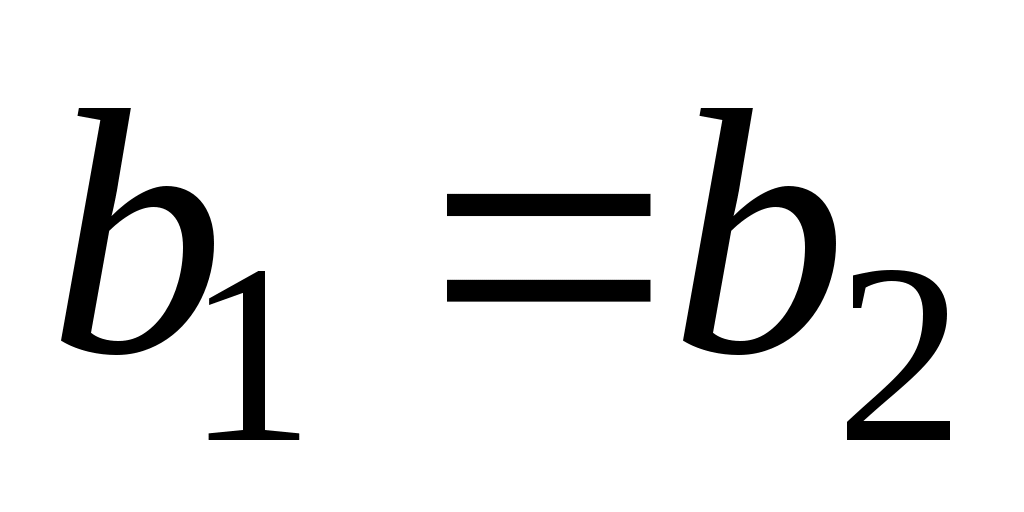 .
.
Р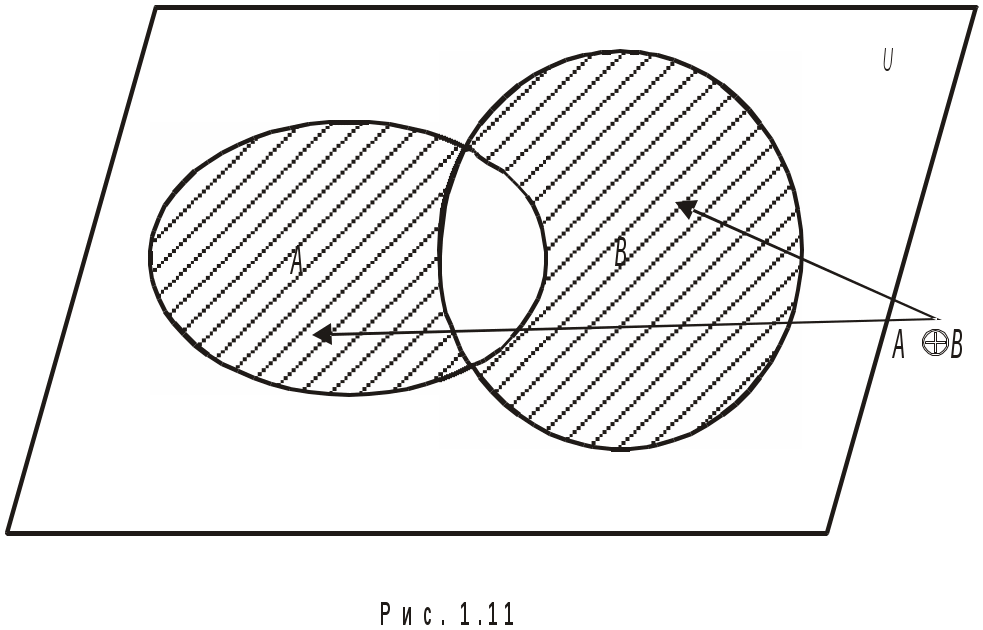
ис. 1.11. Симметрическая разность
Множество, элементами которого являются все упорядоченные пары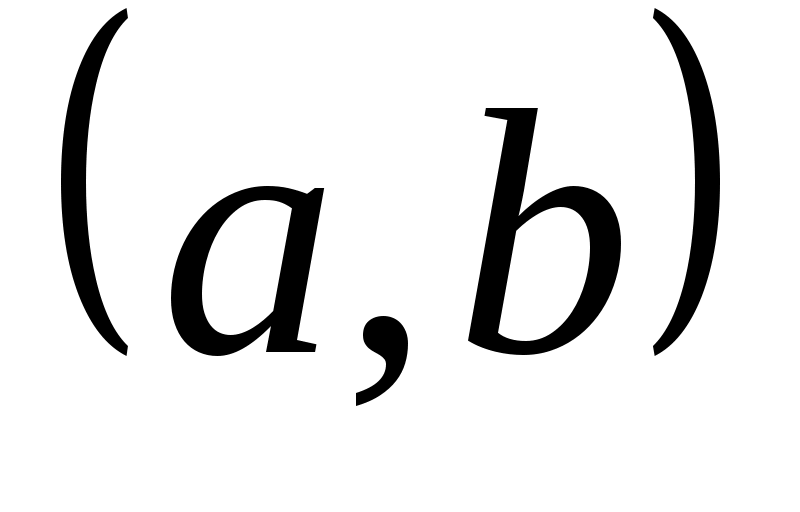 ,
,  ,
, 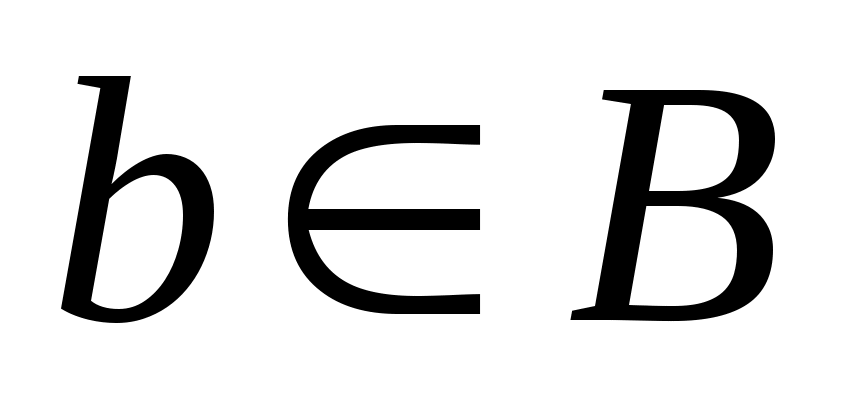 называется прямым или декартовым произведением множеств
называется прямым или декартовым произведением множеств  и
и  и обозначается
и обозначается  . Например,
. Например, 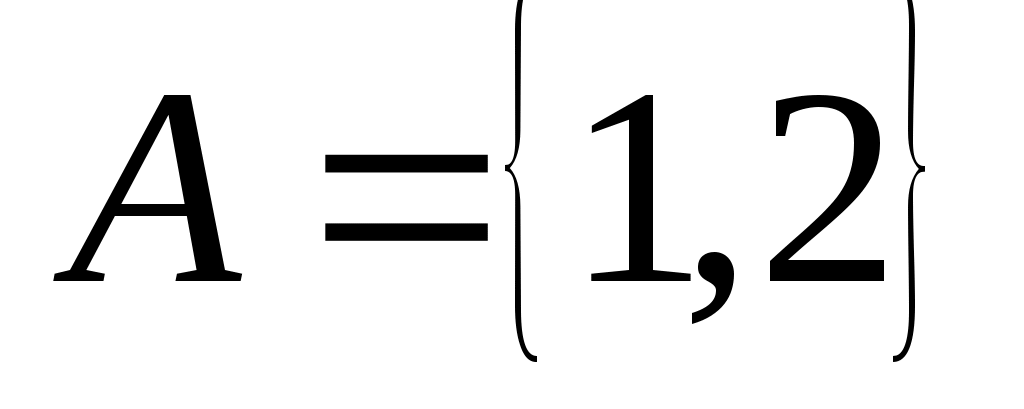 ,
, 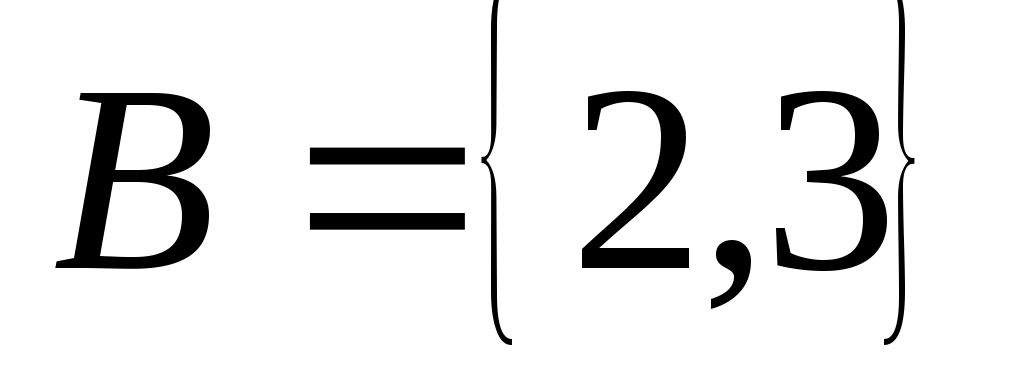

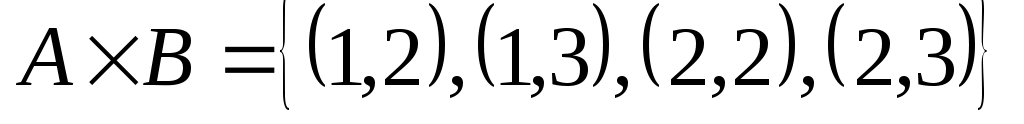 , а
, а 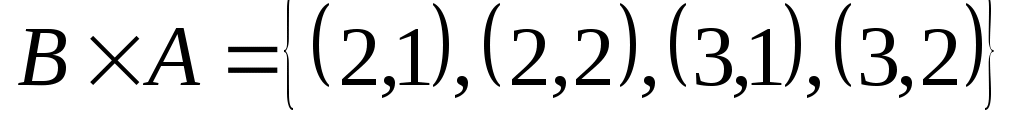 . Таким образом, декартово произведение не подчиняется коммутативному закону, и
. Таким образом, декартово произведение не подчиняется коммутативному закону, и 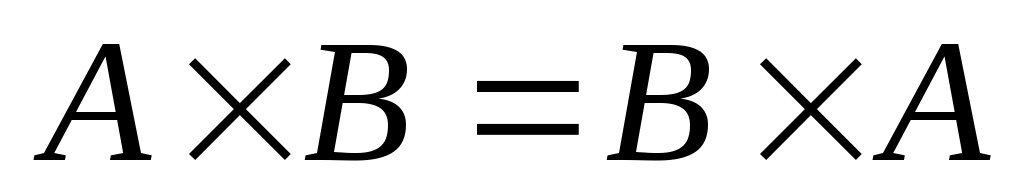 справедливо, если
справедливо, если 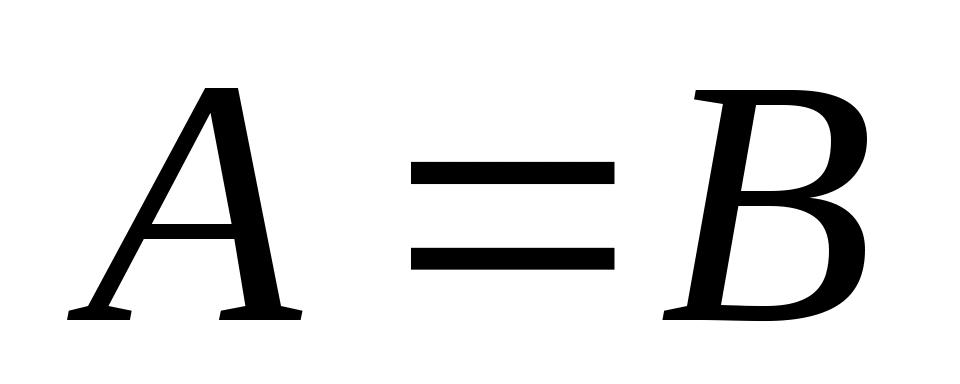 . Произведение
. Произведение 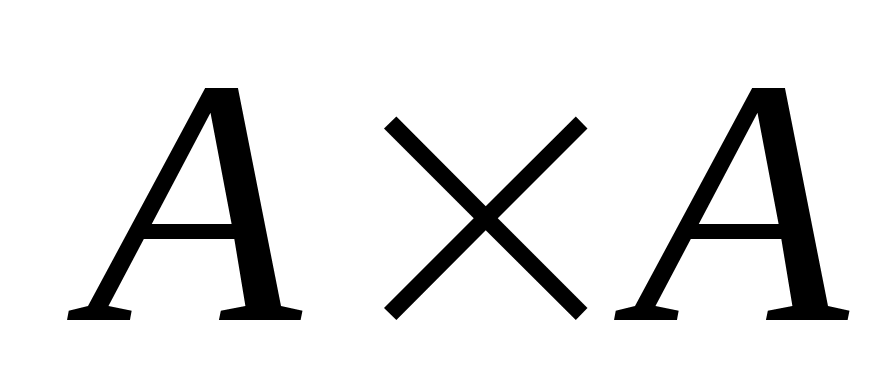 называется декартовым квадратом.
называется декартовым квадратом.
Свойства операций объединения
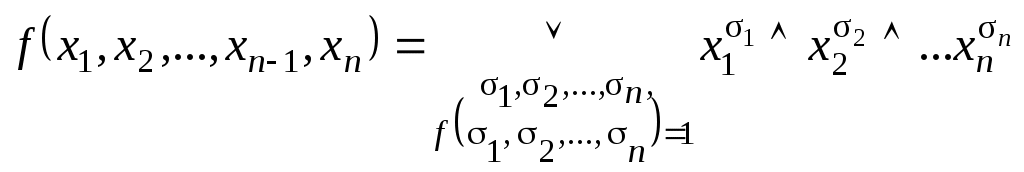 , (1.13.4)
, (1.13.4)где дизъюнкция берется по всевозможным наборам значений переменных
где символ
Аппарат булевых функций используется для проектирования цифровых устройств и базовых элементов компьютерных систем.
1.13.2. Элементы теории множеств
Первичным понятием теории множеств является понятие самого множества. Множество — это совокупность некоторых (произвольных) объектов, объединенных по какому-либо признаку. Элементы множества при этом должны быть различными. Множество обозначается парой скобок
Если каждый элемент множества
является подмножеством множества
Объединение (или сумма). Эта операция над множествами обозначается
Р

ис. 1.7.
Объединение множеств
Рис. 1.8. Пересечение множеств
Пересечением (или произведением) двух множеств называется такое множество
Разностью двух множеств
Рис. 1.9. Разность множеств
Рис. 1.10. Дополнение множества
С

имметрической разностью или кольцевой суммой множеств
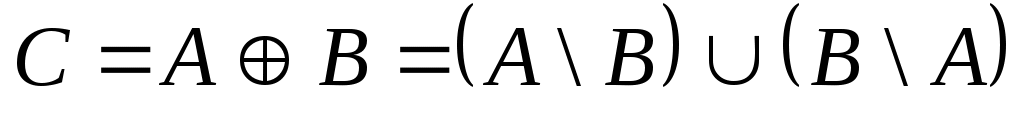 (рис. 1.11). Очевидно, что
(рис. 1.11). Очевидно, что . Если
Р

ис. 1.11. Симметрическая разность
Множество, элементами которого являются все упорядоченные пары
Свойства операций объединения