Файл: Методические указания по темам курса Тема Основные понятия и определения Тема Осевое растяжение (сжатие) кр1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 60
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Новгородский государственный
университет, 2022
Буткин И.А.
СОДЕРЖАНИЕ
Стр.
Введение………………………………………………....…………2
Методические указания по темам курса……………….…………3
Тема 1. Основные понятия и определения……………….…….3
Тема 2. Осевое растяжение (сжатие) КР№1………………….…..4
Тема 3. Сдвиг и кручение (КР№2)…………………. ………..…9
Тема 4. Прямой изгиб (КР№3)……………………………..……12
Список литературы…………………………………………..…...20
Приложения…………………………………………………….....21
ВВЕДЕНИЕ
Сопротивление материалов является одной из наиболее сложных дисциплин в высших учебных заведениях, поэтому при изучении курса рекомендуется вести конспект с кратким изложением теоретического материала и решением типичных задач, рассматриваемых на лекционных и практических занятиях по каждому разделу.
Совершенно необходимо научиться решать задачи самостоятельно. Курс «Сопротивление материалов» дает методику решения наиболее типичных задач.
Представленные методические указания составлены в соответствии с программой учебного модуля по сопротивлению материалов.
Студент заочной формы обучения выполняет три контрольных работы. Варианты заданий выбираются по двум последним цифрам зачетной книжки (если №вар ˃30, то выбирается последняя цифра).
Основные требования при выполнении
контрольных работ
►контрольные работы выполняются либо на пронумерованных листах, сшитых в тетрадь формата А4 (титульный лист выполняется по форме, приведенной в Приложении 1), либо в учебных тетрадях с полями (≈5см) для замечаний преподавателя;
► варианты контрольных работ приведены в Приложении 2;
► вся графическая часть выполняется аккуратно и в масштабе;
► на первой странице должно быть поставлено условие задачи и выполнен рисунок со всеми необходимыми размерами и величинами нагрузок;
► текстовая часть с необходимыми расчетами и дополнительные рисунки, разъясняющие решение задачи, приводятся в произвольной форме c соответствующими пояснениями;
► все физические величины приводить в соответствии с международной системой единиц (СИ)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ТЕМАМ КУРСА
Тема 1. Основные понятия и определения
Дисциплина «Сопротивление материалов» изучает расчет конструкций на прочность
, жесткость и устойчивость при различных видах напряженного состояния.
Для выполнений этих расчетов сначала определяют внутренние силовые факторы, возникающие в поперечных сечениях конструкции под действием внешних сил.
При изучении темы необходимо понять сущность метода сечений, обратить внимание на понятия напряжение и деформация.
Напряжение является мерой внутренних сил, возникающих в теле под действием внешних нагрузок.
Деформация является мерой изменения формы и размеров тела (части тела), возникающих в теле под действием внешних нагрузок, температуры, влажности и пр.
Важно знать, что закон Гука справедлив только в области упругих деформаций. Необходимо понимать запись закона Гука, как в абсолютных, так и относительных единицах.
Сущность метода сечений заключается в том, что тело (элемент конструкции) в интересующем нас месте мысленно рассекается на две части. Одну из частей удаляют, а действие удаленной части на оставшуюся заменяют равнодействующей внутренних сил, возникающих в этом сечении. Таким образом, внутренние силы переходят в разряд внешних сил.
Поскольку все тело находится в равновесии, то и оставшаяся часть также будет находиться в состоянии равновесия, что позволяет составить соответствующие уравнения равновесия и определить равнодействующую внутренних сил.
Вопросы для самопроверки
-
Какие бывают силы? -
Что такое напряжение? -
Что такое деформация? -
Какие деформации называются упругими? -
Какие деформации называются пластическими? -
В чем состоит сущность метода сечений?
Тема 2. Осевое растяжение (сжатие)
В этой теме следует обратить внимание на определение механических характеристик (предел пропорциональности, предел прочности, предел упругости и предел текучести). При этом важно оценить способность материала сопротивляться действию внешних сил.
Пользуясь формулами закона Гука, надо помнить, что этот закон справедлив только в пределах упругих деформаций.
Растяжение и сжатие характеризуются возникновением в поперечных сечениях внутренних сил N.
Центральным растяжением (сжатием) называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила N, а остальные силовые факторы равны нулю.
Явление центрального растяжения (сжатия) возникает в случае, когда все внешние нагрузки действуют по оси, проходящей через центры тяжести поперечных сечений бруса.
1. Внутренние силы N определяют методом сечений. Для этого брус рассекают на отдельные участки, отбрасывают одну из частей, а ее влияние на оставшуюся часть заменяют неизвестной внутренней силой N.
Для каждого сечения составляется уравнение равновесия:
ΣF+N=0, (2.1)
где ΣF– сумма всех внешних сил, находящихся по одну сторону от сечения; N– продольная сила в сечении (внутренняя сила).
Решением уравнения (2.1) определяют величину N.
Для наглядного представления характера (закона) изменения какого-либо из внутренних силовых факторов по длине бруса строят эпюру.
Эпюры представляют собой графики, продольной осью которых является ось бруса, а ординатами – значения определяемых величин (N, σ, ∆l).
2. В поперечных сечениях бруса при центральном растяжении (сжатии)
возникают равномерно распределенные нормальные напряжения σ, равные отношению внутренней продольной силы N к площади A поперечного сечения:
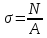 (2.2)
(2.2)Нормальные напряжения при растяжении принимаются положительными, а при сжатии – отрицательными.
Условие прочности в этом случае будет определяться по выражению:
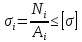 , (2.3)
, (2.3)где
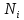 – внутреннее усилие на i – том участке,
– внутреннее усилие на i – том участке, 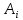 – площадь поперечного сечения i – того участка,
– площадь поперечного сечения i – того участка, 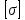 – допускаемое нормальное напряжение.
– допускаемое нормальное напряжение.Отсюда:
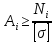 (2.4)
(2.4)3. Под действием растягивающих сил длина l стержня увеличивается на ∆l, а поперечные размеры его уменьшаются. По закону Гука удлинение стержня определяется по формуле:
Δl
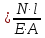 ,(2.5)
,(2.5) где∆l –абсолютное удлинение стержня, l – первоначальная длина стержня, Е – модуль упругости I-го рода.
Последовательность выполнения КР1 разберем на примере:
Пример. Для стального стержня (рис.1) определить во всех сечениях продольную силу N и нормальное напряжение σ. Определить вертикальные перемещения δ для всех поперечных сечений и полное удлинение
Δl стержня. Результаты изобразить графически, построив эпюры N, σ и δ. Модуль продольной упругости материала стержня Е=2105МПа.
Стержень жестко защемлен вверху и нагружен двумя внешними сосредоточенными силами F1=150кН, F2=200кН, приложенными в точках А и С и направленными вдоль его продольной оси. Площади поперечных сечений стержня А1 =18см2 и А2 =12см2.
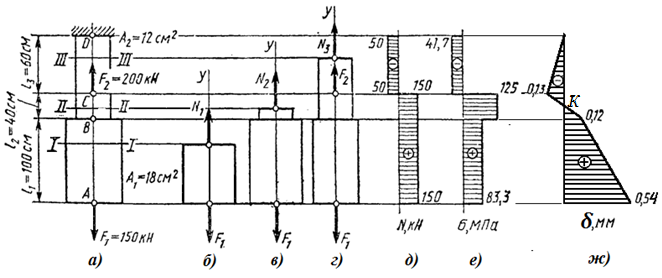
Рис.1 Пример выполнения графической части КР1
Решение:
Разобьём стержень на отдельные участки, начиная со свободного конца. Границами участков считаются сечения, в которых приложены внешние силы, или меняются площади поперечных сечений.
В нашем случае наблюдаются следующие участки:
- участок АВ – участок от точки приложения силы F1 (точка А) до сечения, в котором меняется площадь поперечного сечения (точка В).
- участок ВС – от точки В до сечения, где приложена сила F2 (точка С).
- участок СД – от точки приложения силы F2 до верхней опоры (точка D – точка подвеса).
Для определения внутреннего усилия N мысленно разрезаем стержень по сечениям I–I , II–IIи III – III.
Из условия равновесия части стержня ниже сечения I–I (рис.1,б) получим:
N1 – F1= 0, откуда N1=F1 =150кН (растяжение)
Из условия равновесия части стержня ниже сечения II–II(рис.1,в) получим:
N2 – F1= 0, откуда N2=F1 =150кН (растяжение)
Из условия равновесия части стержня ниже сечения III–III(рис.1,г) получим:
N3+F2 – F1= 0, откуда N3=F1 – F2 =150 –200= –50кН (сжатие)
Зная продольную силу на каждом из трёх участков, определяем значения нормальных напряжений:
σ1 =
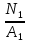 =
=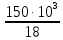 = 8,33103
= 8,33103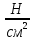 = 83,3 ·106
= 83,3 ·106 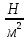
= 83,3МПа
σ2 =
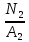 =
=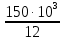 = 12,5103
= 12,5103 = 125 МПа
= 125 МПаσ3 =
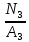 =
=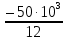 = – 4,17103
= – 4,17103 = – 41,7МПа
= – 41,7МПаПо найденным значениям N и σ строим (в масштабе) эпюры продольных сил (рис.1,д) и нормальных напряжений (рис.1,е).
Из построений видно, что:
– эпюра продольных сил всегда имеет скачки в сечениях, где приложены или внешние силы, или расположены опоры. Причем, величина скачка равна или величине самой внешней силы, или величине реакции опоры;
– эпюра интенсивности нормальных напряжений всегда имеет скачки не только в сечениях, где наблюдаются скачки продольных сил, но и в местах изменения площади поперечного сечения стержня;
– наиболее опасным является участок ВС, поскольку на этом участке действуют максимальные нормальные напряжения(σ2
 = 125 МПа).
= 125 МПа).Эпюры штрихуются линиями перпендикулярными к продольной линии. В этом случае длина штрихов определяет в масштабе величину продольной силы или напряжения в соответствующем сечении бруса.
Для определения полного удлинения стержня находим перемещения характерных точек: А, В и С. При этом вычисления удобнее вести от точки D, поскольку она остается неподвижной (δD=0)и эту точку можно принять за начало координат.
ΔС = Δl3 =
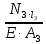 =
= 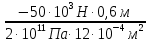 = –1,25 10-4м ≈ – 0,13мм (вверх);
= –1,25 10-4м ≈ – 0,13мм (вверх);δВ = δС +Δl2= – 0,1310-3
 +
+ 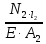 = – 0,1310-3 +
= – 0,1310-3 + 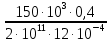 =
== – 0,1310-3 + 2,510-4 = 0,1210-3м = 0,12мм (вниз);
δA= δВ+Δl1= 0,1210-3 +