Файл: Методические указания по темам курса Тема Основные понятия и определения Тема Осевое растяжение (сжатие) кр1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 61
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
{\displaystyle d}d:
Ix =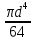
; Wx = 
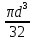(4.4)
{\displaystyle J_{x}={\frac {\pi d^{4}}{64}}}{\displaystyle W_{x}={\frac {\pi d^{3}}{32}}}Для прямоугольного сечения высотой h{\displaystyle h} и шириной {\displaystyle b} b:
{\displaystyle J_{x}={\frac {bh^{3}}{3}}}Ix =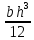
; Wx = 
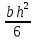(4.5)
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}Для более сложных сечений ( швеллер, двутавр), имеющих стандартные размеры, эти величины приведены в справочной литературе. Надо ясно представлять пути (возможности) увеличения момента сопротивления сечения без увеличения расхода материала.
Изгибающий момент в сечении может быть определен методом сечений.
Для наглядного представления о законах изменения поперечной силы Qу и изгибающего момента Мx по длине балки удобно изображать их в виде графиков (эпюр), ординаты которых соответствуют значениям поперечных сил и изгибающих моментов в любом ее сечении.
Построение эпюр производится следующим образом.
Линию, параллельную оси балки (ось Z) , принимают за ось абсцисс (нулевая линия), от которой в произвольном масштабе откладывают ординаты, соответствующие значениям Qу или Мх в различных сечениях балки. Соединяя концы отложенных ординат, получаем эпюры Qу и Мx, соответственно.
Ординаты, выражающие величины положительных Qу и Мx, принято откладывать вверх от осиZ, а отрицательных – вниз (студенты строительных специальностей положительные величины изгибающих моментов откладывают вниз).
Штриховать эпюры следует только вертикальными линиями, поскольку каждая линия штриховки в принятом масштабе выражает величину Qу или Мх в данном сечении. Рекомендуется проверять правильность построения эпюр, используя дифференциальную зависимость между Qу и Мx.
Порядок выполнения работы:
1. Определяют опорные реакции балки.
2. Обозначают характерные сечения (точки) балки. Ими являются:
концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки.
3. Для построения эпюры поперечных сил Qу определяют значения поперечных сил в характерных точках.
Необходимо помнить, что:
поперечная сила в сечении равна сумме проекций всех сил, расположенных по одну сторону от сечения, на ось ординат (ось Y), которая перпендикулярна к оси элемента.
Сила, расположенная слева от рассматриваемого сечения и направленная вверх, считается положительной, а сила, направленная вниз, – отрицательная, для правой части балки знаки меняются наоборот (Рис.4.1а).
Найденные значения поперечных сил в характерных точках отложим в масштабе от нулевой линии. Эти значения соединяем соответствующими линиями, руководствуясь правилами:
а) если на участке балки распределенная нагрузка отсутствует (q=0), то под этим участком Qу = const и эпюра представляет собой прямую, параллельную нулевой линии;
б) если на участке балки приложена распределенная нагрузка, причем q=const, то под этим участком поперечная сила меняется по линейному закону.
Соединив все значения поперечных сил по указанным правилам, получим эпюру Qу .
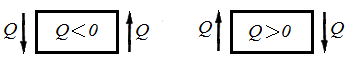
а)
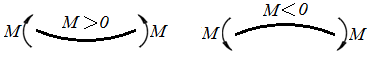
б)
Рис.4.1 Знаки поперечных сил а) и изгибающих моментов б) при изгибе
4. Для построения эпюры изгибающих моментов Мх определяем изгибающие моменты в характерных сечениях.
Необходимо помнить, что:
изгибающий момент в рассматриваемом сечении равен сумме моментов от всех сил (распределенных, сосредоточенных, в том числе и опорных реакций), а также внешних сосредоточенных моментов, расположенных по одну сторону от сечения.
Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки относительно рассматриваемого сечения по часовой стрелке, то они образуют положительный изгибающий момент, а если против часовой стрелки
– отрицательный изгибающий момент. Для правой части – наоборот (рис.4.1б).
Полученные значения откладывают в масштабе от нулевой линии. Соединяют концы отложенных ординат, руководствуясь следующими правилами:
а) если на участке нет распределенной нагрузки (q=0), то на этом участке изгибающий момент меняется по линейному закону (концы отложенных ординат соединяются прямой линией);
б) если на участке балки отсутствует поперечная сила (Qу=0), то на этом участке Мх = const;
в) на участке балки, где приложена распределенная нагрузка, изгибающий момент изменяется по параболе. Парабола имеет выпуклость навстречу действия нагрузки, т.е. при действии нагрузки сверху вниз парабола обращена выпуклостью вверх;
г) если эпюра Qу на рассматриваемом участке не пересекает нулевую линию, то эпюра Мх может быть построена по двум точкам, так как все значения изгибающих моментов в промежуточных сечениях участка находятся между значениями в характерных сучениях (на границах участка);
д) если эпюра Qу пересекает нулевую линию (меняет знак), то под этим сечением эпюра Мх будет иметь экстремум (максимальное или минимальное значение) или вершину параболы. Положение этого сечения находят по эпюре Qу (из подобия треугольников определяют координату сечения, где Qу=0). Затем находят значение изгибающего момента в этом сечении и строят эпюру Мх на участке с распределенной нагрузкой по трем точкам.
Соединив все полученные точки по указанным выше правилам, получают график изменения изгибающих моментов по длине балки. Этот график называется эпюрой Мх.
Методику построения эпюр Qу и Мх рассмотрим на конкретном примере:
Пример. Построить эпюры Qу и Мх для балки, изображенной на рис. 4.2.
Решение:
1) используя уравнения равновесия, определяем опорные реакции балки:
ΣМА = 0 МА = Р(а+b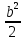)+q
– q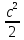
+VВ(c+d)+M = 0,
Откуда: VВ =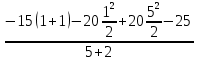
= 26,4кН
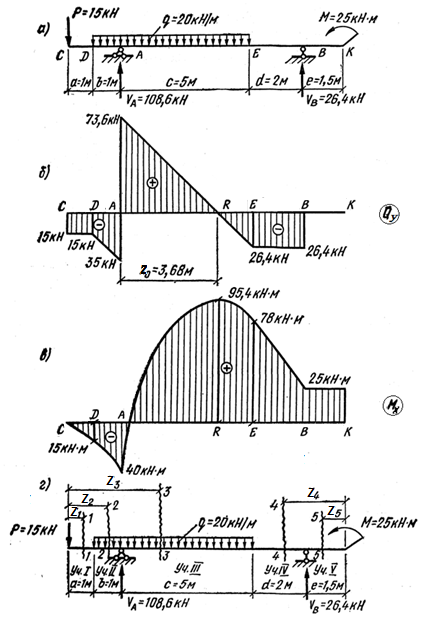
Рис.4.2 Пример построения эпюр поперечных сил и изгибающих моментов для балки, работающей на изгиб.
ΣМВ = 0 МВ = Р(а+b+с+d)+q(b+c)(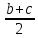
+d) – VA(c+d)+M = 0,
Откуда: VA=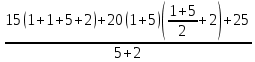
= 108,6кН
Проверка: ΣРу = 0 –15–20(1+ 5) +108,6 +26,4 = 0
Построение эпюры Q:
QC = QD = – P= – 15кН;
QAлев = – P – qb= – 15– 20·1= – 35кH;
QAправ= – VB+qc = – 26,4 + 20·5 = 73,6кН;
QE =QBлев= – VB= – 26,4кН;
QBправ = QК = 0
Строим эпюру Qу, откладывая положительные значения ординат вверх от оси Z, а отрицательные - вниз (рис.4.2,б).
Из графических построений видно, что на участке АЕ эпюра Qy пересекает продольную ось балки в точке R. Из подобия треугольников, образовавшихся на этом участке эпюры Qy (с = 5 м), определим расстояние z0 от левой опоры до сечения, в котором Q = 0, т.е. решаем пропорцию:
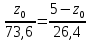
Расчет показывает: z0 = 3,68м.
Построение эпюры Мx.
Составляем уравнения изгибающих моментов по каждому участку.
Участок I
Проводим сечение 1-1 на расстоянии z1 от начала координат (точка С).
Изгибающий момент М1 определяем по выражению:
М1 = –Р·z1,где 0 ≤ z1 ≤ a
Уравнение показывает, что на участке I наблюдается линейная зависимость М1 от z1, при этом: МС = 0 , MD= –15кНм.
Участок II
Проводим сечение 2-2 на расстоянии z2 от начала координат.
Изгибающий момент М2 определяем по выражению:
М2= –Р·z2 –q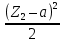
, где a ≤ z2 ≤ (a + b)
Величина изгибающего момента:
- в (·) D (при z2= a= 1м) МD= –15кНм;
- в (·) А (при z2 = a+b= 2м)MA= – 40кНм
При этом наблюдается параболическая зависимость М2от z2.
Участок III
Проводим сечение 3-3 на расстоянии z3 от начала координат.
Изгибающий момент М3 определяем по выражению:
М3 = –Р·z3–q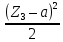
+VA (z3– (a+b),где (a+b) ≤ z3 ≤ (a+b+c)
Величина изгибающего момента:
- в (·) А (при z3= a+b= 2м)MA= – 40кНм
- в (·) R(при z3= a+b+z0 = 5,68м) МR= 95,4кНм – экстремум;
- в (·) Е (при z3 = a+b+с= 7м) МЕ = 78кНм
Участок IV
Для упрощения вычислений участок IV будем рассматривать справа (по схеме). Для этого проводим сечение 4-4 на расстоянии z4 от начала координат (точка К).
Изгибающий момент М4 определяем по выражению:
М4 = М+VВ (z4– e),гдеe ≤ z4≤ (e+d)
Величина изгибающего момента:
- в (·) B(при z4 = e= 1,5м)MB= 25кНм;
- в (·) E(при z4 = e+d= 3,5м) МE= 78кНм
При этом наблюдается линейная зависимость М4 от z4.
Участок V
Проводим сечение 5-5 на расстоянии z5 от начала координат (точка К).
Изгибающий момент М5 определяем по выражению:
М5
Ix =
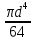; Wx = 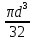(4.4){\displaystyle J_{x}={\frac {\pi d^{4}}{64}}}{\displaystyle W_{x}={\frac {\pi d^{3}}{32}}}Для прямоугольного сечения высотой h{\displaystyle h} и шириной {\displaystyle b} b:
{\displaystyle J_{x}={\frac {bh^{3}}{3}}}Ix =
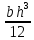; Wx = 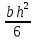(4.5){\displaystyle W_{x}={\frac {bh^{2}}{6}}}Для более сложных сечений ( швеллер, двутавр), имеющих стандартные размеры, эти величины приведены в справочной литературе. Надо ясно представлять пути (возможности) увеличения момента сопротивления сечения без увеличения расхода материала.
Изгибающий момент в сечении может быть определен методом сечений.
Для наглядного представления о законах изменения поперечной силы Qу и изгибающего момента Мx по длине балки удобно изображать их в виде графиков (эпюр), ординаты которых соответствуют значениям поперечных сил и изгибающих моментов в любом ее сечении.
Построение эпюр производится следующим образом.
Линию, параллельную оси балки (ось Z) , принимают за ось абсцисс (нулевая линия), от которой в произвольном масштабе откладывают ординаты, соответствующие значениям Qу или Мх в различных сечениях балки. Соединяя концы отложенных ординат, получаем эпюры Qу и Мx, соответственно.
Ординаты, выражающие величины положительных Qу и Мx, принято откладывать вверх от осиZ, а отрицательных – вниз (студенты строительных специальностей положительные величины изгибающих моментов откладывают вниз).
Штриховать эпюры следует только вертикальными линиями, поскольку каждая линия штриховки в принятом масштабе выражает величину Qу или Мх в данном сечении. Рекомендуется проверять правильность построения эпюр, используя дифференциальную зависимость между Qу и Мx.
Порядок выполнения работы:
1. Определяют опорные реакции балки.
2. Обозначают характерные сечения (точки) балки. Ими являются:
концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки.
3. Для построения эпюры поперечных сил Qу определяют значения поперечных сил в характерных точках.
Необходимо помнить, что:
поперечная сила в сечении равна сумме проекций всех сил, расположенных по одну сторону от сечения, на ось ординат (ось Y), которая перпендикулярна к оси элемента.
Сила, расположенная слева от рассматриваемого сечения и направленная вверх, считается положительной, а сила, направленная вниз, – отрицательная, для правой части балки знаки меняются наоборот (Рис.4.1а).
Найденные значения поперечных сил в характерных точках отложим в масштабе от нулевой линии. Эти значения соединяем соответствующими линиями, руководствуясь правилами:
а) если на участке балки распределенная нагрузка отсутствует (q=0), то под этим участком Qу = const и эпюра представляет собой прямую, параллельную нулевой линии;
б) если на участке балки приложена распределенная нагрузка, причем q=const, то под этим участком поперечная сила меняется по линейному закону.
Соединив все значения поперечных сил по указанным правилам, получим эпюру Qу .
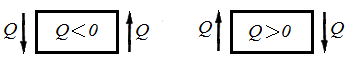
а)
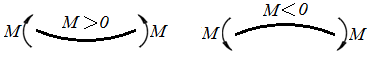
б)
Рис.4.1 Знаки поперечных сил а) и изгибающих моментов б) при изгибе
4. Для построения эпюры изгибающих моментов Мх определяем изгибающие моменты в характерных сечениях.
Необходимо помнить, что:
изгибающий момент в рассматриваемом сечении равен сумме моментов от всех сил (распределенных, сосредоточенных, в том числе и опорных реакций), а также внешних сосредоточенных моментов, расположенных по одну сторону от сечения.
Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки относительно рассматриваемого сечения по часовой стрелке, то они образуют положительный изгибающий момент, а если против часовой стрелки
– отрицательный изгибающий момент. Для правой части – наоборот (рис.4.1б).
Полученные значения откладывают в масштабе от нулевой линии. Соединяют концы отложенных ординат, руководствуясь следующими правилами:
а) если на участке нет распределенной нагрузки (q=0), то на этом участке изгибающий момент меняется по линейному закону (концы отложенных ординат соединяются прямой линией);
б) если на участке балки отсутствует поперечная сила (Qу=0), то на этом участке Мх = const;
в) на участке балки, где приложена распределенная нагрузка, изгибающий момент изменяется по параболе. Парабола имеет выпуклость навстречу действия нагрузки, т.е. при действии нагрузки сверху вниз парабола обращена выпуклостью вверх;
г) если эпюра Qу на рассматриваемом участке не пересекает нулевую линию, то эпюра Мх может быть построена по двум точкам, так как все значения изгибающих моментов в промежуточных сечениях участка находятся между значениями в характерных сучениях (на границах участка);
д) если эпюра Qу пересекает нулевую линию (меняет знак), то под этим сечением эпюра Мх будет иметь экстремум (максимальное или минимальное значение) или вершину параболы. Положение этого сечения находят по эпюре Qу (из подобия треугольников определяют координату сечения, где Qу=0). Затем находят значение изгибающего момента в этом сечении и строят эпюру Мх на участке с распределенной нагрузкой по трем точкам.
Соединив все полученные точки по указанным выше правилам, получают график изменения изгибающих моментов по длине балки. Этот график называется эпюрой Мх.
Методику построения эпюр Qу и Мх рассмотрим на конкретном примере:
Пример. Построить эпюры Qу и Мх для балки, изображенной на рис. 4.2.
Решение:
1) используя уравнения равновесия, определяем опорные реакции балки:
ΣМА = 0 МА = Р(а+b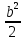)+q
– q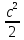
+VВ(c+d)+M = 0,
Откуда: VВ =
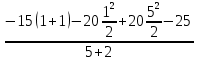= 26,4кН Рис.4.2 Пример построения эпюр поперечных сил и изгибающих моментов для балки, работающей на изгиб.
ΣМВ = 0 МВ = Р(а+b+с+d)+q(b+c)(
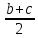+d) – VA(c+d)+M = 0,Откуда: VA=
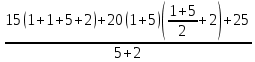= 108,6кНПроверка: ΣРу = 0 –15–20(1+ 5) +108,6 +26,4 = 0
Построение эпюры Q:
QC = QD = – P= – 15кН;
QAлев = – P – qb= – 15– 20·1= – 35кH;
QAправ= – VB+qc = – 26,4 + 20·5 = 73,6кН;
QE =QBлев= – VB= – 26,4кН;
QBправ = QК = 0
Строим эпюру Qу, откладывая положительные значения ординат вверх от оси Z, а отрицательные - вниз (рис.4.2,б).
Из графических построений видно, что на участке АЕ эпюра Qy пересекает продольную ось балки в точке R. Из подобия треугольников, образовавшихся на этом участке эпюры Qy (с = 5 м), определим расстояние z0 от левой опоры до сечения, в котором Q = 0, т.е. решаем пропорцию:
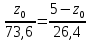
Расчет показывает: z0 = 3,68м.
Построение эпюры Мx.
Составляем уравнения изгибающих моментов по каждому участку.
Участок I
Проводим сечение 1-1 на расстоянии z1 от начала координат (точка С).
Изгибающий момент М1 определяем по выражению:
М1 = –Р·z1,где 0 ≤ z1 ≤ a
Уравнение показывает, что на участке I наблюдается линейная зависимость М1 от z1, при этом: МС = 0 , MD= –15кНм.
Участок II
Проводим сечение 2-2 на расстоянии z2 от начала координат.
Изгибающий момент М2 определяем по выражению:
М2= –Р·z2 –q
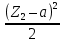, где a ≤ z2 ≤ (a + b)Величина изгибающего момента:
- в (·) D (при z2= a= 1м) МD= –15кНм;
- в (·) А (при z2 = a+b= 2м)MA= – 40кНм
При этом наблюдается параболическая зависимость М2от z2.
Участок III
Проводим сечение 3-3 на расстоянии z3 от начала координат.
Изгибающий момент М3 определяем по выражению:
М3 = –Р·z3–q
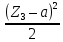+VA (z3– (a+b),где (a+b) ≤ z3 ≤ (a+b+c)Величина изгибающего момента:
- в (·) А (при z3= a+b= 2м)MA= – 40кНм
- в (·) R(при z3= a+b+z0 = 5,68м) МR= 95,4кНм – экстремум;
- в (·) Е (при z3 = a+b+с= 7м) МЕ = 78кНм
Участок IV
Для упрощения вычислений участок IV будем рассматривать справа (по схеме). Для этого проводим сечение 4-4 на расстоянии z4 от начала координат (точка К).
Изгибающий момент М4 определяем по выражению:
М4 = М+VВ (z4– e),гдеe ≤ z4≤ (e+d)
Величина изгибающего момента:
- в (·) B(при z4 = e= 1,5м)MB= 25кНм;
- в (·) E(при z4 = e+d= 3,5м) МE= 78кНм
При этом наблюдается линейная зависимость М4 от z4.
Участок V
Проводим сечение 5-5 на расстоянии z5 от начала координат (точка К).
Изгибающий момент М5 определяем по выражению:
М5