Файл: Методические указания по темам курса Тема Основные понятия и определения Тема Осевое растяжение (сжатие) кр1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 64
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 0,1210-3 +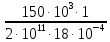 
=
= 0,1210-3 + 4,1710-4 = 0,5410-3м = 0,54мм (вниз)
Из эпюры перемещений (рис.1ж) видно, что некоторое сечение (точка К) не перемещается. Сечения, расположенные выше точки К, перемещаются вверх (сжатие); сечения, расположенные ниже точки К, перемещаются вниз (растяжение).
Полное удлинение стержня составляет величину Δl = 0,54мм
Вопросы для самопроверки
13. В чём заключается сущность метода сечений?
14. Что представляет собой эпюра продольных сил?
15. По какой формуле вычисляются нормальные напряжения в сечениях балки?
16. Как определить абсолютное удлинение стержня?
Тема 3. Сдвиг и кручение
Кручение ‒ один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор ‒ крутящий момент Мкр. Примеры кручения: пружины растяжения-сжатия, валы.
Угол Δφ закручивания цилиндрического стержня в границах упругих деформаций под действием момента Мкр может быть определён из уравнения закона Гука для случая кручения:
{\displaystyle \varphi _{}={T\ell \over J_{0}G},} Δφ =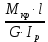
, (3.1){\displaystyle \varphi _{}={T\ell \over J_{0}G},}{\displaystyle \varphi _{}={T\ell \over J_{0}G},}
где: {\displaystyle J_{0}}Ip
=
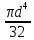– полярный момент инерции; d{\displaystyle \ell } ‒ диаметр стержня; l– длина стержня; G– модуль сдвига (модуль упругости II-го рода) .
Отношение угла закручивания Δφ к длине {\displaystyle \ell }l называют относительным углом закручивания Θ:
Θ=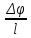
(3.2){\displaystyle \theta ={\frac {\varphi }{\ell }}}
Деформация кручения является частным случаем деформации сдвига.
Касательные напряжения {\displaystyle \tau _{r}}τ, возникающие в условиях кручения, определяются по формуле:
τ =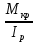
{\displaystyle \tau _{r}={T\cdot r \over J_{0· ρ, (3.3)
где ρ – расстояние от оси кручения.
Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при {\displaystyle r_{max}=R} ρ = d/2 и при максимальном крутящем моменте {\displaystyle T_{max}}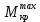
. Это даёт возможность записать условие прочности при кручении в таком виде:
τ =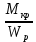
≤ [τ], (3.4) {\displaystyle \tau _{max}={T_{max}\cdot R \over J_{0}}={\frac {T_{max}}{W_{p}}}}
где Wp =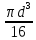
— полярный момент сопротивления; [τ] ‒ допускаемые касательные напряжения.{\displaystyle \tau _{max}={\frac {T_{max}}{W_{p}}}\leq [\tau ]}
Условие жесткости при кручении выглядит так:
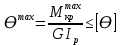(3.5)
где [Ө] – допускаемый относительный угол закручивания.
Используя эти условия, можно или по известным силовым факторам, которые создают крутящий момент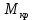
, найти полярный момент сопротивления Ip и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот ‒ зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.
При изучении деформации от сдвига необходимо обратить внимание на полную аналогию между формулами закона Гука при растяжении (сжатии) и при сдвиге, а также понять, что явление сдвига нельзя рассматривать отдельно от растяжения (сжатия).
В случае кручения в поперечных сечениях возникают только касательные напряжения, которые распределяются по сечению неравномерно, изменяясь по линейному закону от ”0” в центре сечения до максимального значения на наружном контуре сечения.
Касательные напряжения в двух взаимно перпендикулярных сечениях равны по величине и противоположны по знаку. Это свойство касательных напряжений называют законом парности касательных напряжений.
При выполнении расчетов на кручение следует понять основные правила построения эпюр крутящих моментов, используя метод сечений, а также построение эпюр углов закручивания.
Указания к выполнению КР2
3. Для определения максимального крутящего момента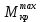
необходимо из условия равновесия:
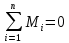(3.6)
определить величину и направление неизвестного крутящего момента M0.
Для этого необходимо вал разбить на участки. Границами участков являются сечения, в которых приложены крутящие моменты (в настоящем задании расчетная схема состоит из 4-х участков).
4. Начинать рассматривать вал можно с любой стороны с учетом знака каждого крутящего момента. (крутящий момент считается положительным, если при рассматривании со стороны сечения он действует против хода часовой стрелки и наоборот).
5. Используя метод сечений, вычислить величину крутящего момента на каждом участке (величина крутящего момента на каждом участке равна сумме крутящих моментов, действующих по одну сторону от сечения).
6. По полученным результатам необходимо построить эпюру крутящих моментов по длине вала и определить наиболее опасный участок (участок, где действует ).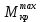
7. Определить диаметр вала из условия прочности (3.4).
8. На каждом участке вычислить относительнный угол закручивания и сравнить с допускаемым [Ө].
9. При необходимости вычислить диаметр вала из условия жесткости.
10. Построить эпюру углов закручивания.
Вопросы для самопроверки
Тема 4. Поперечный изгиб прямого бруса
Эта тема является самой большой и самой сложной, ее следует изучать постепенно.
Изгиб ‒ вид деформации, при котором происходит изменение кривизны продольных осей брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов и поперечных сил.
Если при изгибе в поперечном сечении бруса действует только изгибающий момент Мx, то соответственно имеется чистый изгиб. Если в поперечном сечении действует также и поперечная сила Qy, то имеется поперечный изгиб.
Прямой изгиб бруса возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.
Таким образом, кривизна изогнутой оси балки связана с изгибающим моментом выражением:
{\displaystyle {\frac {1}{\rho }}={\frac {M_{x}}{EJ_{x}}}}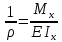
(4.1)
Распределение нормальных напряжений по высоте сечения выражается формулой:
{\displaystyle \sigma ={\frac {M_{x}}{J_{x}}}y}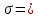
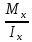·y (4.2)
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}Максимальное напряжение в сечении выражается формулой:
{\displaystyle \sigma _{max}={\frac {M_{x}}{J_{x}}}{\frac {h}{2}}={\frac {M_{x}}{W_{x}}}} σmax = ·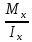
= 
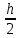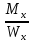, (4.3)
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}где {\displaystyle W_{x}={\frac {J_{x}}{\frac {h}{2}}}} ρ ‒ радиус изгиба продольной оси бруса; Ix ‒ момент инерции поперечного сечения бруса; Wx ‒ момент сопротивления сечения изгибу; h ‒ {\displaystyle h} высота сечения балки.
Величины {\displaystyle J_{x}}Ix и {\displaystyle W_{x}}Wx для простых сечений (круглое, прямоугольное) вычисляются аналитически. Для круглого сечения диаметром
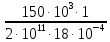== 0,1210-3 + 4,1710-4 = 0,5410-3м = 0,54мм (вниз)
Из эпюры перемещений (рис.1ж) видно, что некоторое сечение (точка К) не перемещается. Сечения, расположенные выше точки К, перемещаются вверх (сжатие); сечения, расположенные ниже точки К, перемещаются вниз (растяжение).
Полное удлинение стержня составляет величину Δl = 0,54мм
Вопросы для самопроверки
-
Как строится диаграмма растяжения? -
Дать определение продольной силы. -
Как определить знак продольной силы N? -
Что называется пределом прочности? -
Что называется пределом пропорциональности? -
Что называется пределом текучести? -
Что называется пределом упругости? -
Как формулируется закон Гука при растяжении? -
Что показывает модуль упругости 1-го рода при растяжении (сжатии)? -
Что такое коэффициент Пуассона? -
Как строятся эпюры продольных сил и деформаций? -
От каких факторов зависит величина запаса прочности и чем она характеризуется?
13. В чём заключается сущность метода сечений?
14. Что представляет собой эпюра продольных сил?
15. По какой формуле вычисляются нормальные напряжения в сечениях балки?
16. Как определить абсолютное удлинение стержня?
Тема 3. Сдвиг и кручение
Кручение ‒ один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор ‒ крутящий момент Мкр. Примеры кручения: пружины растяжения-сжатия, валы.
Угол Δφ закручивания цилиндрического стержня в границах упругих деформаций под действием момента Мкр может быть определён из уравнения закона Гука для случая кручения:
{\displaystyle \varphi _{}={T\ell \over J_{0}G},} Δφ =
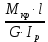, (3.1){\displaystyle \varphi _{}={T\ell \over J_{0}G},}{\displaystyle \varphi _{}={T\ell \over J_{0}G},}где: {\displaystyle J_{0}}Ip
=
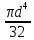– полярный момент инерции; d{\displaystyle \ell } ‒ диаметр стержня; l– длина стержня; G– модуль сдвига (модуль упругости II-го рода) .Отношение угла закручивания Δφ к длине {\displaystyle \ell }l называют относительным углом закручивания Θ:
Θ=
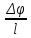(3.2){\displaystyle \theta ={\frac {\varphi }{\ell }}}Деформация кручения является частным случаем деформации сдвига.
Касательные напряжения {\displaystyle \tau _{r}}τ, возникающие в условиях кручения, определяются по формуле:
τ =
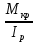{\displaystyle \tau _{r}={T\cdot r \over J_{0· ρ, (3.3) где ρ – расстояние от оси кручения.
Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при {\displaystyle r_{max}=R} ρ = d/2 и при максимальном крутящем моменте {\displaystyle T_{max}}
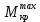. Это даёт возможность записать условие прочности при кручении в таком виде:τ =
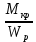≤ [τ], (3.4) {\displaystyle \tau _{max}={T_{max}\cdot R \over J_{0}}={\frac {T_{max}}{W_{p}}}}где Wp =
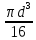— полярный момент сопротивления; [τ] ‒ допускаемые касательные напряжения.{\displaystyle \tau _{max}={\frac {T_{max}}{W_{p}}}\leq [\tau ]}Условие жесткости при кручении выглядит так:
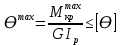(3.5)где [Ө] – допускаемый относительный угол закручивания.
Используя эти условия, можно или по известным силовым факторам, которые создают крутящий момент
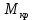, найти полярный момент сопротивления Ip и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот ‒ зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.При изучении деформации от сдвига необходимо обратить внимание на полную аналогию между формулами закона Гука при растяжении (сжатии) и при сдвиге, а также понять, что явление сдвига нельзя рассматривать отдельно от растяжения (сжатия).
В случае кручения в поперечных сечениях возникают только касательные напряжения, которые распределяются по сечению неравномерно, изменяясь по линейному закону от ”0” в центре сечения до максимального значения на наружном контуре сечения.
Касательные напряжения в двух взаимно перпендикулярных сечениях равны по величине и противоположны по знаку. Это свойство касательных напряжений называют законом парности касательных напряжений.
При выполнении расчетов на кручение следует понять основные правила построения эпюр крутящих моментов, используя метод сечений, а также построение эпюр углов закручивания.
Указания к выполнению КР2
-
Чтобы ответить на поставленные вопросы, необходимо найти опасный участок вала, т.е. участок с наибольшим крутящим моментом. -
Условие прочности и условие жесткости выражаются формулами (3.4) и (3.5) , соответственно.
3. Для определения максимального крутящего момента
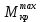необходимо из условия равновесия: 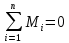(3.6)определить величину и направление неизвестного крутящего момента M0.
Для этого необходимо вал разбить на участки. Границами участков являются сечения, в которых приложены крутящие моменты (в настоящем задании расчетная схема состоит из 4-х участков).
4. Начинать рассматривать вал можно с любой стороны с учетом знака каждого крутящего момента. (крутящий момент считается положительным, если при рассматривании со стороны сечения он действует против хода часовой стрелки и наоборот).
5. Используя метод сечений, вычислить величину крутящего момента на каждом участке (величина крутящего момента на каждом участке равна сумме крутящих моментов, действующих по одну сторону от сечения).
6. По полученным результатам необходимо построить эпюру крутящих моментов по длине вала и определить наиболее опасный участок (участок, где действует
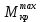).7. Определить диаметр вала из условия прочности (3.4).
8. На каждом участке вычислить относительнный угол закручивания и сравнить с допускаемым [Ө].
9. При необходимости вычислить диаметр вала из условия жесткости.
10. Построить эпюру углов закручивания.
Вопросы для самопроверки
-
Что называется абсолютным и относительным сдвигом? -
Как формулируется закон Гука при сдвиге? -
Что характеризует модуль упругости II рода? -
Запишите формулу условия прочности заклепочного соединения. -
Какие напряжения возникают в поперечных сечениях круглого вала при кручении? -
Как производится расчет вала на прочность при кручении? -
Как строятся эпюры крутящих моментов и углов закручивания? -
В чем разница между абсолютным и относительным углом закручивания? -
Как производится расчет вала на жесткость при кручении?
Тема 4. Поперечный изгиб прямого бруса
Эта тема является самой большой и самой сложной, ее следует изучать постепенно.
Изгиб ‒ вид деформации, при котором происходит изменение кривизны продольных осей брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов и поперечных сил.
Если при изгибе в поперечном сечении бруса действует только изгибающий момент Мx, то соответственно имеется чистый изгиб. Если в поперечном сечении действует также и поперечная сила Qy, то имеется поперечный изгиб.
Прямой изгиб бруса возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.
Таким образом, кривизна изогнутой оси балки связана с изгибающим моментом выражением:
{\displaystyle {\frac {1}{\rho }}={\frac {M_{x}}{EJ_{x}}}}
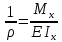(4.1)Распределение нормальных напряжений по высоте сечения выражается формулой:
{\displaystyle \sigma ={\frac {M_{x}}{J_{x}}}y}
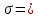
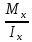·y (4.2){\displaystyle W_{x}={\frac {bh^{2}}{6}}}
{\displaystyle W_{x}={\frac {bh^{2}}{6}}}Максимальное напряжение в сечении выражается формулой:
{\displaystyle \sigma _{max}={\frac {M_{x}}{J_{x}}}{\frac {h}{2}}={\frac {M_{x}}{W_{x}}}} σmax =
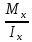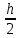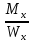· = , (4.3){\displaystyle W_{x}={\frac {bh^{2}}{6}}}где {\displaystyle W_{x}={\frac {J_{x}}{\frac {h}{2}}}} ρ ‒ радиус изгиба продольной оси бруса; Ix ‒ момент инерции поперечного сечения бруса; Wx ‒ момент сопротивления сечения изгибу; h ‒ {\displaystyle h} высота сечения балки.
Величины {\displaystyle J_{x}}Ix и {\displaystyle W_{x}}Wx для простых сечений (круглое, прямоугольное) вычисляются аналитически. Для круглого сечения диаметром