Файл: Федеральное агентство по рыболовству Федеральное государственное бюджетное образовательное.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 103

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Техническое задание

1. Структурная схема системы электросвязи и назначение её отдельных элементов

2. Расчеты по заданной функции корреляции исходного сообщения

3. Расчет средней квадратической погрешности фильтрации (СКПФ) сообщения, средней мощности отклика ИФНЧ, частоты и интервала временной дискретизации отклика ИФНЧ

4. Расчет интервала квантования, порогов и уровней квантования, средней квадратической погрешности квантования (СКПК)

5. Расчет закона и функции распределения вероятностей квантованного сигнала, а также энтропии, производительности и избыточности L - ичного дискретного источника

6. Кодирование значения L-ичного дискретного сигнала двоичным блочным примитивным кодом. Построение таблицы кодовых расстояний кода

7. Расчет нормированного к амплитуде переносчика спектра модулированного сигнала и его начальной ширины спектра. Построение в масштабе графика нормированного спектра сигнала дискретной модуляции

8. Расчет мощности и амплитуды модулированного сигнала, дисперсии (мощности) аддитивной помехи в полосе частот сигнала, пропускную способность НКС

12. Решение оптимизационной задачи. Определение оптимальной энергетической ширины спектра сообщения, доставляющей минимум относительной суммарной СКП его восстановления



В виду того, что выбор начальной энергетической ширины спектра исходного сообщения не приводит к минимуму ОСКПВ виду того что погрешность фильтрации , шум квантования и шум передачи - независимые случайные процессы, то суммарная СКП восстановления непрерывного сообщения будет равна сумме СКП (см формулу (48).

Тогда относительная суммарная СКП (ОСКП) восстановления сообщения очевидно равна:
(50)
Нетрудно показать, что относительные СКП фильтрации , квантования и передачи зависят от энергетической ширины спектра сообщения различным образом. С учетом полученных выше соотношений имеем:




(51),
где Kq= =0.083 (см. задание 4);

KП=Ky=1.083 определяется выражением:

KX (fA), PОШ (fA) - функции переменной fA, находятся как:


Pош=0.5е-0.5 h2


Из теории известно, что суммарная величина относительной СКП восстановления переданного сообщения имеет минимум при оптимально выбранной энергетической ширине спектра исходного сообщения.


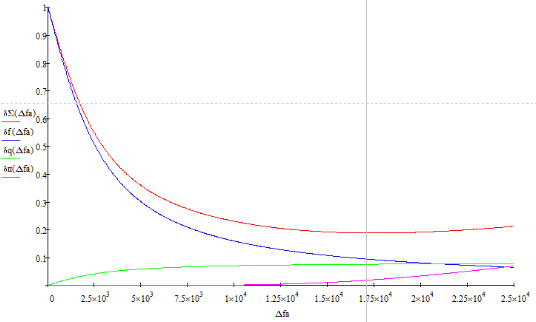
Рисунок 25 - График зависимости ОСКП от энергетической ширины спектра сообщения
Оптимальная энергетическая ширина спектра сообщения видна на интервале f= [12500; 24000] Гц.

Алгоритм решения задачи:

Для решения поставленной задачи используем MathCAD 14.0.




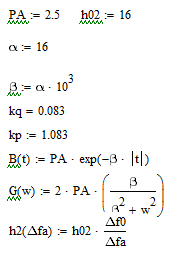
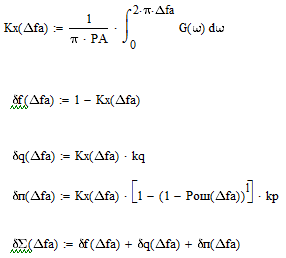
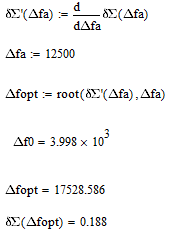
Заключение



В данной работе мы изучили принципы построения систем электросвязи и расчёта их параметров. При расчете первых трех заданий мы рассмотрели структурную схему электросвязи, изучили функцию корреляции, рассчитали интервал корреляции , спектр плотности мощности и начальную энергетическую ширину спектра плотности сообщения , построили графики (рис.2, рис.3). В процессе выполнения заданий 1, 2, 3 рассчитали среднюю квадратическую погрешность фильтрации сообщения , среднюю мощность отклика ИФНЧ и изобразили сигналы и спектры на входе и выходе дискретизатора ЦАП (рис.5-7).

В заданиях № 4-6 при заданных значениях числа уровней квантования и средней мощности отклика рассчитали интервал , пороги (табл.2) и уровни (табл.3) квантования. Изучили характеристики квантования (рис.8), определили энтропию , производительность (скорость ввода информации в ДКС) , избыточность источника и функцию распределения вероятностей. Рассчитали априорные вероятности передачи по двоичному дискретному каналу связи, начальную ширину спектра сигнала ИКМ и построили графики (рис.9-14).

При выполнении заданий 7, 8, 9 изучили принципы расчета характеристик и параметров сигналов дискретной модуляции, узкополосного непрерывного гауссовского канала связи, а также научились оценивать помехоустойчивость и эффективность приема сигналов дискретной модуляции. Рассчитали ширину спектра сигнала ДАМ, мощность, приходящуюся в среднем на один двоичный символ Р=616.8 Вт, амплитуду модулированного сигнала U = 35.12 В, пропускную способность канала С = 422149.016, среднею вероятность ошибки Pош=2.765*10-4, энтропию ошибочных решений, скорость передачи информации по дискретному каналу связи R=23911,975, эффективность системы передачи Э=0.042. Построили графики спектра сигнала ДАМ (рис.15), ФПВ аддитивной гауссовой помехи (рис.16), ФПВ огибающей помехи (рис.17), ФПВ суммы сигнала и помехи (рис.18), ФПВ огибающей суммы (рис. 19).

В процессе выполнения заданий 10-11 изучили числовые характеристики сигнала, рассчитали скорость передачи информации по L-ичному ДКС , величину относительных потерь в скорости , дисперсию случайных импульсов шума передачи , среднюю квадратическую погрешность шума передачи (СКПП) = 0.014, суммарную начальную СКП восстановления непрерывного сообщения (СКПП) = 1,097 Вт, относительную СКП (ОСКП)  = 0.439. Построили в масштабе сравнительный график закона распределения вероятностей отклика декодера и закона распределения вероятностей отклика квантователя (рис.21), изобразили сигналы на выходе декодера и интерполятора ЦАП, а также восстановленного сообщения на выходе системы электросвязи (рис.22-24). Определили, что в интервале времени от t=1.57 до t=1.8 мс сигнал на выходе лучше всего повторяет исходный.

В задании 12 решили оптимизационную задачу: с помощью MathCAD 14 определили оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления. Построили график зависимости ОСКП от энергетической ширины спектра сообщения (рис.25).

Список литературы





  1. В.Г. Санников - Методические рекомендации по выполнению курсовой работы-М.: 1996.

  2. Самоучитель MathCad 14 Автор: Макаров Е.Г. Издательство: Новый Диск Год издания: 2008

  3. Зюко А.Г., Кловский В.Г. Теория электрической связи. - М.: Изд-во Радио и связь, 1998.





Смотрите также файлы