М инистерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего образования

«Пермский национальный исследовательский политехнический университет»

Кафедра микропроцессорных средств автоматизации

Синтез системы управления двигателем постоянного тока с регуляторами класса «вход-выход» в программной среде MexBIOS

Методическое руководство к выполнению

Лабораторной работы № 2 по учебной дисциплине “Системы управления электроприводом”

Составил: д.т.н., профессор кафедры МСА Казанцев В.П.
Пермь, 2022 г.

Цели работы:

Синтез системы управления двигателем постоянного тока (ДПТ) с регуляторами класса «вход-выход» по принципу подчиненного регулирования в программной среде MexBIOS.
Краткие теоретические сведения и описание работы:

1. Расчет параметров двигателя

Математическое описание двигателя постоянного тока с постоянным возбуждением можно представить в следующем виде:

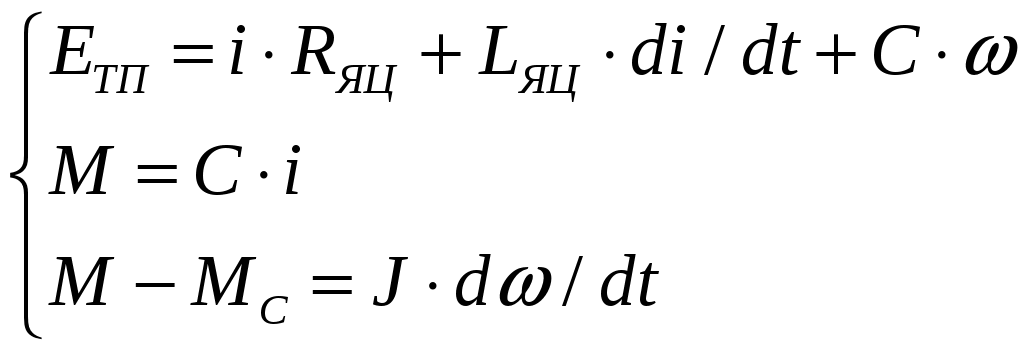, (1)

где E_ТП – ЭДС источника питания; i, M, ω– координаты следящего электропривода: ток, электромагнитный момент и скорость соответственно; R_ЯЦ – сопротивление якорной цепи; L_ЯЦ – индуктивность якорной цепи; С – постоянная двигателя; М_С – момент на валу двигателя; J – момент инерции двигателя.

На рисунке 1 представлена схема, соответствующая математическому описанию (1).

---

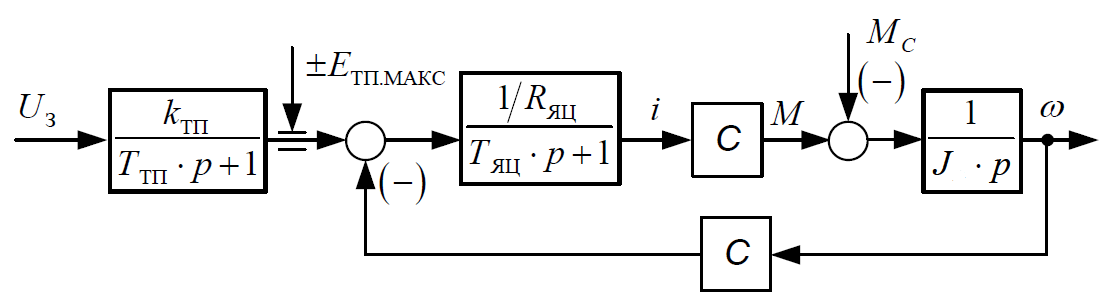
Рисунок 1 – Структурная схема двигателя постоянного тока с питанием от транзисторного преобразователя

На рисунке 1 обозначены:

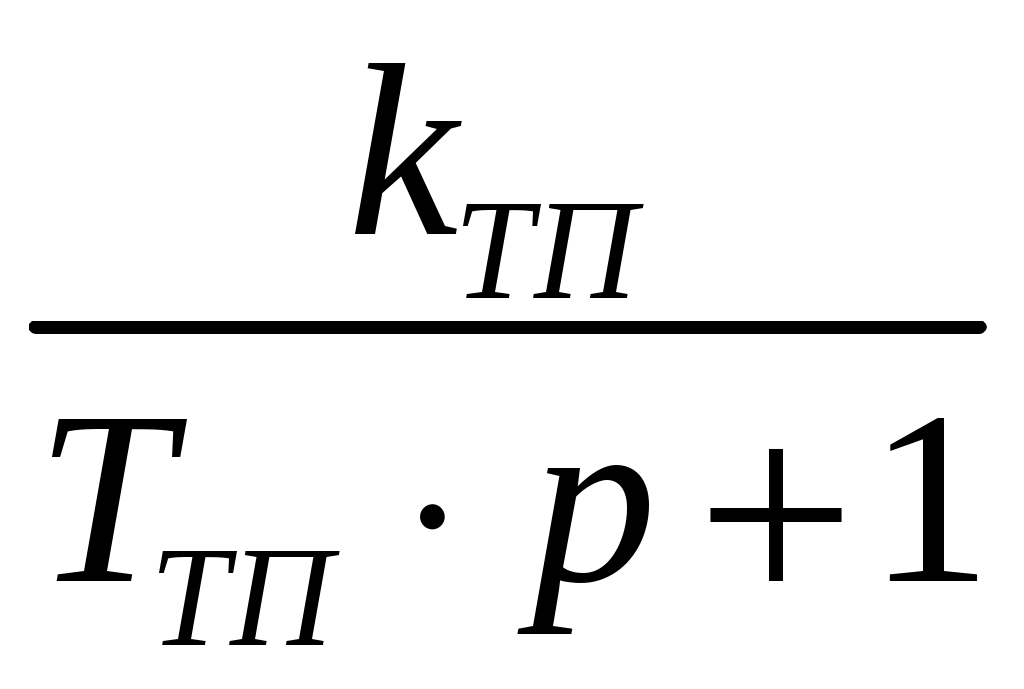– передаточная функция транзисторного преобразователя с широтно-импульсной модуляцией (ШИМ);

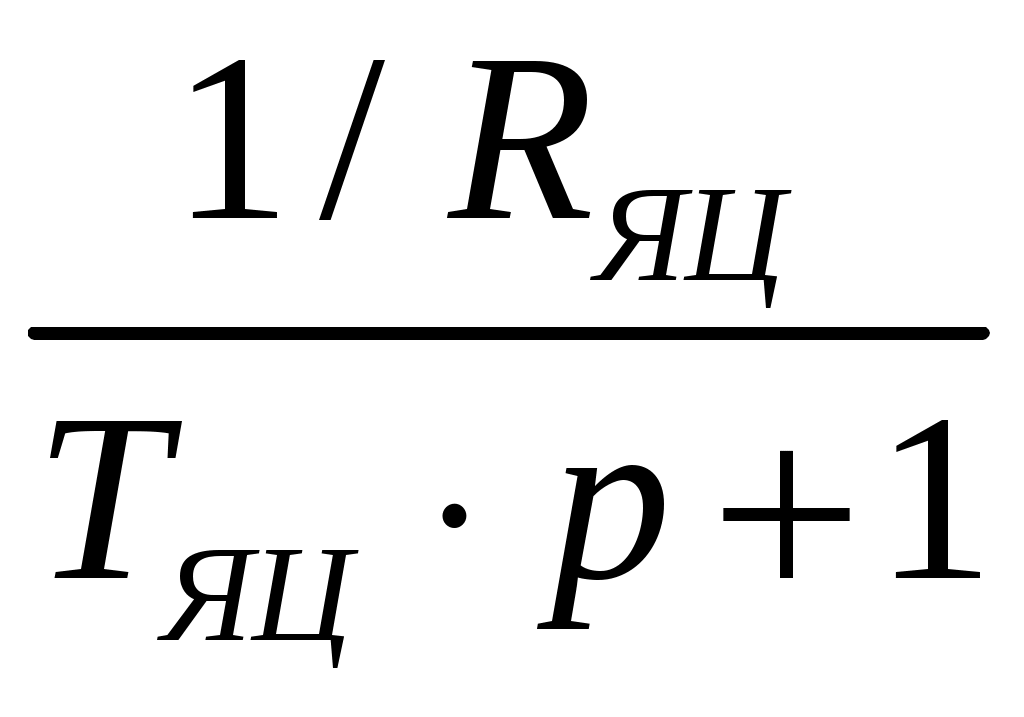– передаточная функция якорной цепи.

Для настройки системы управления необходимо знать параметры двигателя. Часть параметров дана в таблице с вариантами (таблица 1), другие необходимо рассчитать самостоятельно по представленным ниже формулам.
Таблица 1. Параметры ДПТ для заданных вариантов

№ вар.	Параметры ДПТ
	Uн (В)	Iн (А)	RЯЦ (Ом)	LЯЦ (Гн)	J (кг⋅м2)	B	н (1/с)	Ттп (с)	kтп (о.е.)	zp	TS	Brake
1	52	15	0,5	0,00053	0,00022	0,001	125,6	0,0001	51	1	0,00001	0
2	52	15	0,5	0,00053	0,00022	0,001	125,6	0,0001	51	1	0,00001	0
3	110	75	0,1	0,00011	0,00111	0,001	125,6	0,0001	100	1	0,00001	0
4	110	75	0,1	0,00011	0,00111	0,001	210	0,0001	100	1	0,00001	0
5	220	50	0,3	0,00032	0,00074	0,01	314	0,0002	210	1	0,00001	0
6	220	50	0,4	0,00042	0,00074	0,01	210	0,0002	210	1	0,00001	0
7	440	200	0,1	0,00011	0,00296	0,01	314	0,0002	430	1	0,00001	0
8	440	200	0,1	0,00011	0,00296	0,01	210	0,0002	430	1	0,00001	0
9	600	1000	0,04	0,00004	0,01481	0,01	157	0,0002	590	1	0,00001	0
10	600	1000	0,04	0,00004	0,01481	0,01	157	0,0002	590	1	0,00001	0
11	440	100	0,25	0,00027	0,00148	0,01	210	0,0002	430	1	0,00001	0
12	440	100	0,25	0,00027	0,00148	0,01	210	0,0002	430	1	0,00001	0
13	220	20	1,5	0,0016	0,00030	0,001	314	0,0001	210	1	0,00001	0
14	220	20	1,5	0,0016	0,00030	0,001	210	0,0001	210	1	0,00001	0
15	440	160	0,3	0,00032	0,00237	0,01	314	0,0002	430	1	0,00001	0
16	220	10	1,0	0,0011	0,00015	0,001	314	0,0001	210	1	0,00001	0
17	220	10	1,0	0,0011	0,00015	0,001	314	0,0001	210	1	0,00001	0

---

, (2)

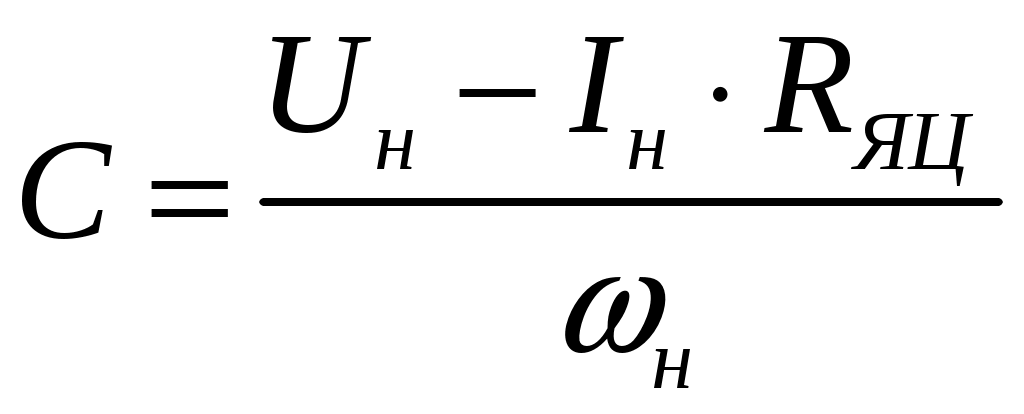. (3)

2. Настройка контура тока

Структурная схема контура тока представлена на рисунке 2 (а). Здесь инерционность преобразователя учтена за счет введения апериодического звена, но не учтена его дискретность и квантование по времени. Обратная связь представлена в общем виде коэффициентом k_T.

Данный контур теоретически можно настроить по методике Кесслера на модальный оптимум, обеспечивая предельное быстродействие при перерегулировании на уровне 4,3%, приняв за малую некомпенсируемую постоянную времени величину . Полоса пропускания контура тока по управлению рассчитывается по следующей формуле:

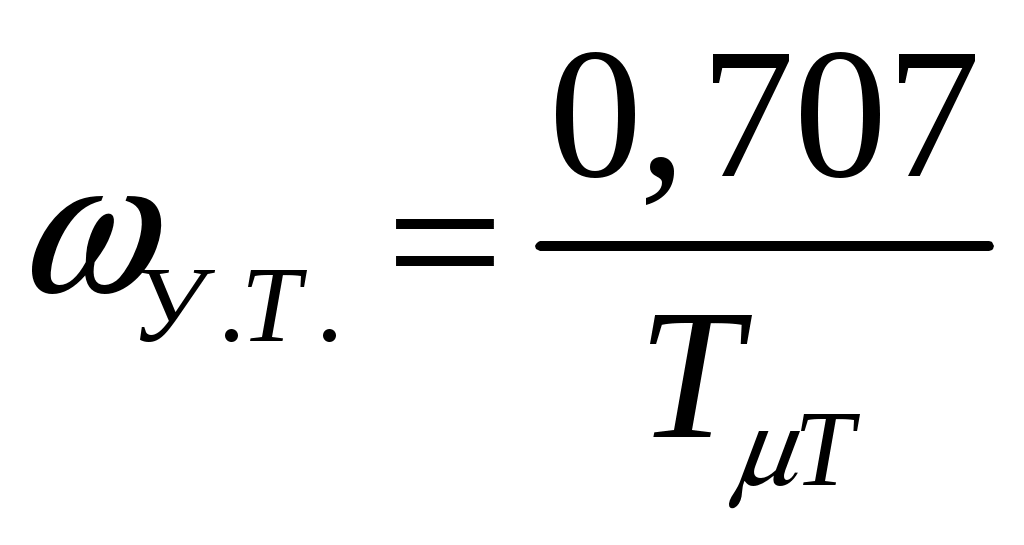. (4)

Также при настройке системы необходимо сделать следующее допущение – обратную связь считаем безынерционной и настроенной на коэффициент k_T = 1, требуемая полоса пропускания в контуре тока f_У.Т. = 200 Гц.



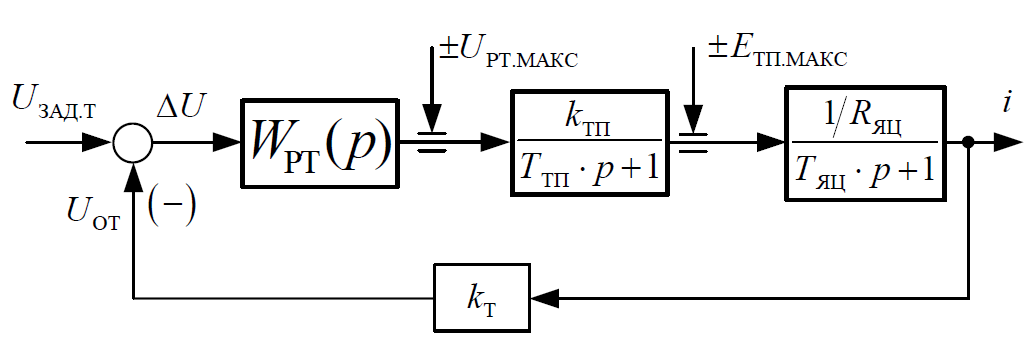
(а)



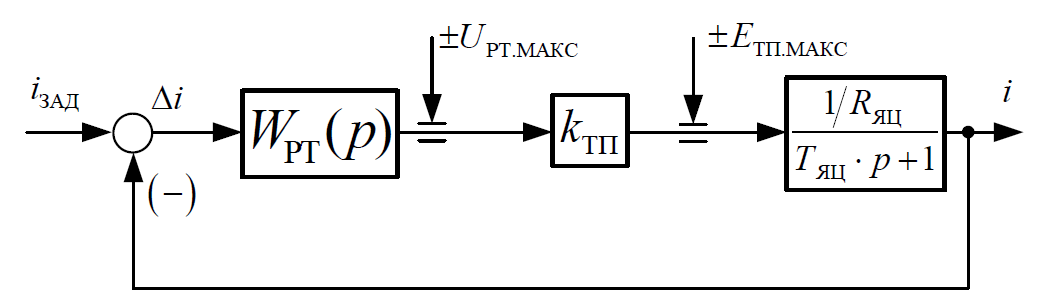
(б)

Рисунок 2 – Структурная схема контура тока

Контур на рисунке 2 (б) можно настроить на апериодический процесс.

Передаточная функция объекта управления контура тока:

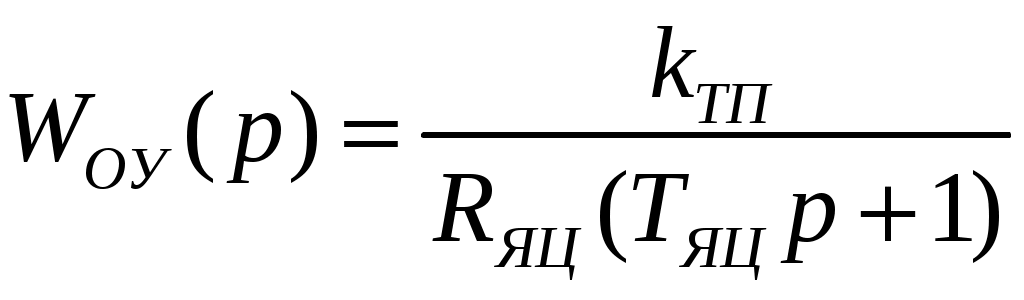, (5)

желаемые передаточные функции замкнутого и разомкнутого контуров тока:

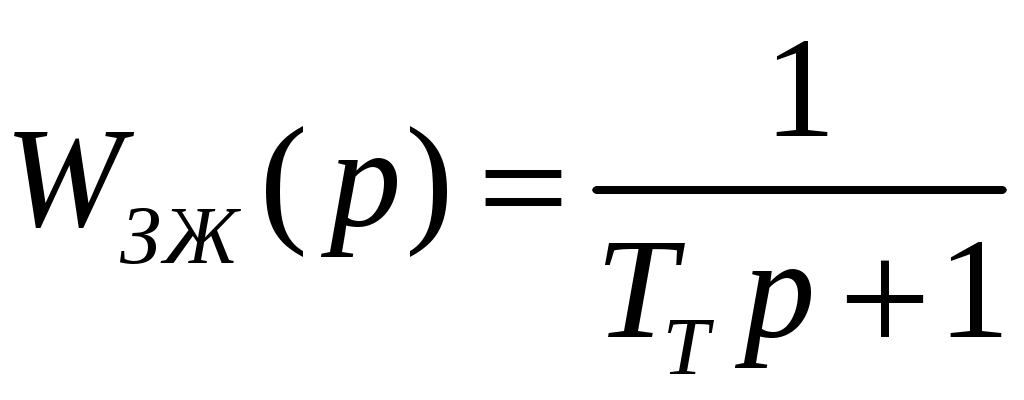, (6)

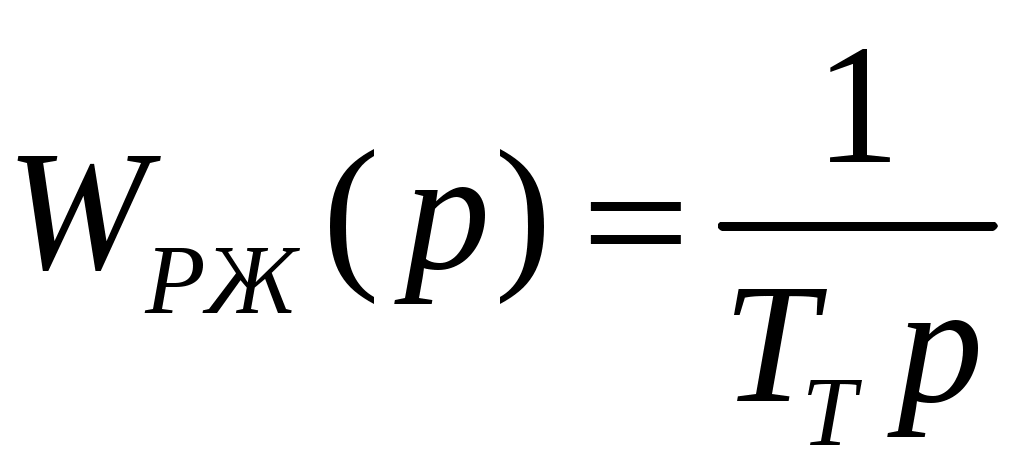, (7)

где T_T = 1/ω_У.Т. = 1/(2π⋅200) = 0,8⋅10^-3 – желаемая постоянная времени контура тока (данная величина одинакова для всех вариантов).

Определяем тогда передаточную функцию регулятора тока:

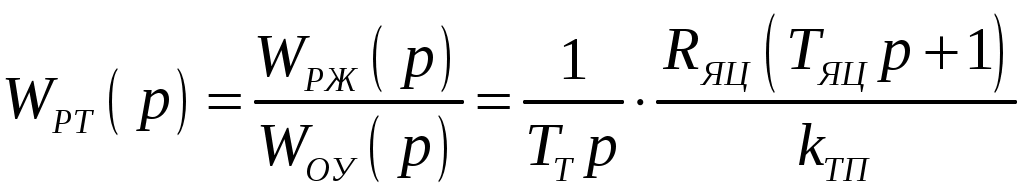. (8)

Передаточная функция соответствует ПИ-регулятору:

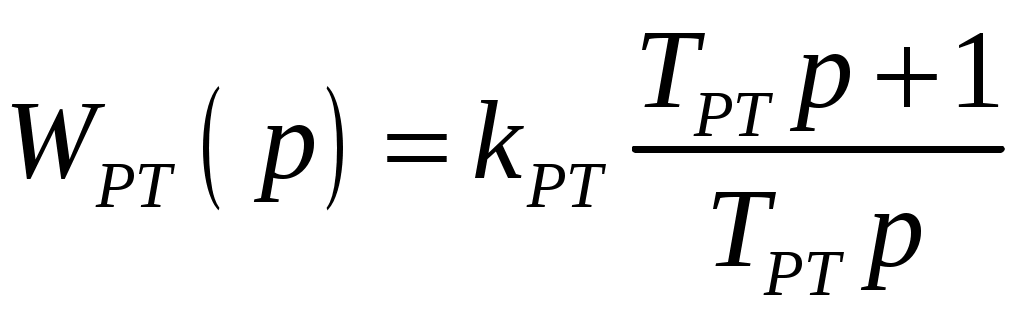. (9)

Определяем параметры регулятора:

---

; (10)

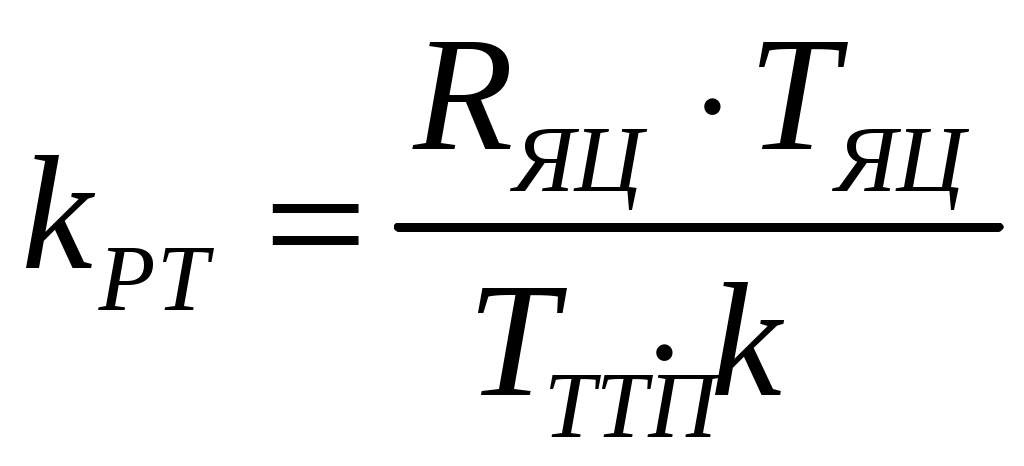. (11)

Для дискретной модели регулятора необходимо дополнительно выполнить расчет коэффициента интегральной составляющей:

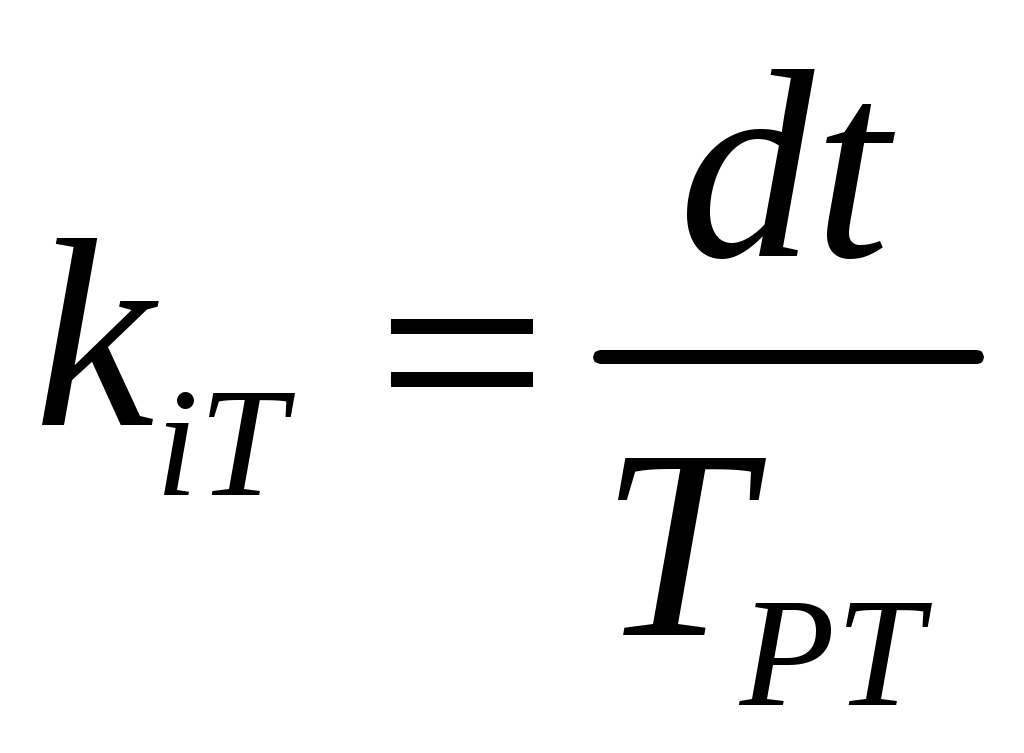, (12)

где dt = T_S – шаг расчета системы управления по времени.

3. Настройка контура скорости

Настройку контура скорости произведем на симметричный оптимум.

Структурная схема контура скорости с ПИ-регулятором скорости и замкнутым контуром тока (6), оптимизированным выше, показана на рисунке 3.



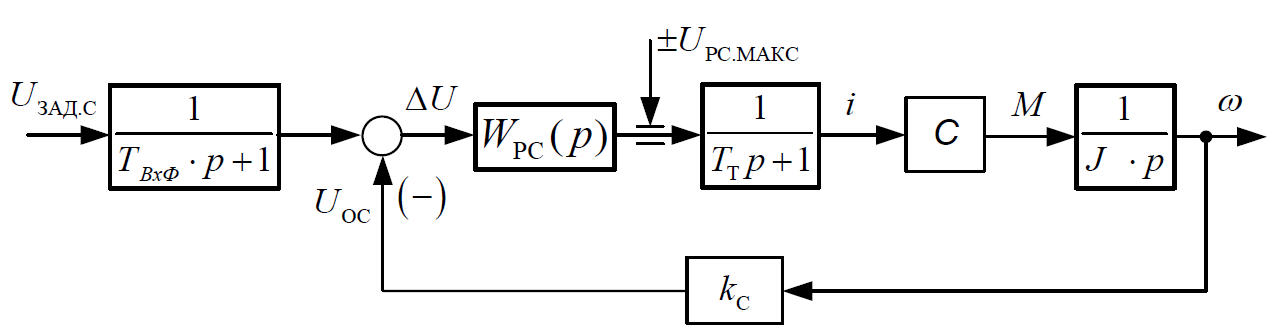
Рисунок 3 – Структурная схема контура скорости
Малая некомпенсируемая постоянная времени контура скорости равна постоянной времени внутреннего контура тока:

. (13)

Коэффициент обратной связи по скорости:

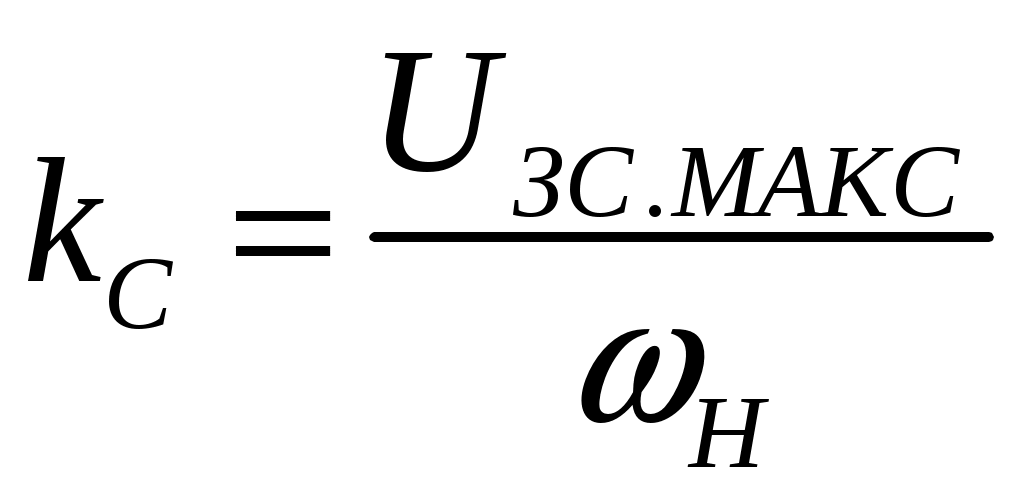, (14)

где U_{ЗС.МАКС} = 1 о.е. – максимальное задание на скорость.

Коэффициент усиления ПИ-регулятора скорости находим следующим образом:

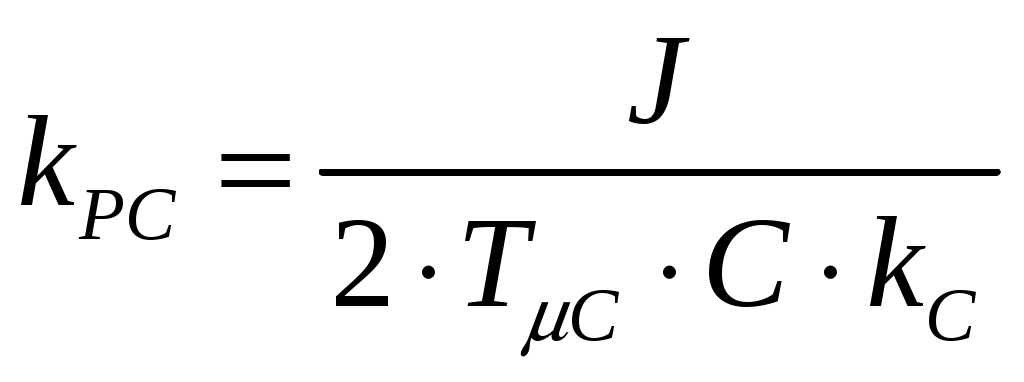. (15)

Постоянную времени регулятора находим следующим образом:

. (16)

Интегральную составляющую ПИ-регулятора рассчитываем по формуле:

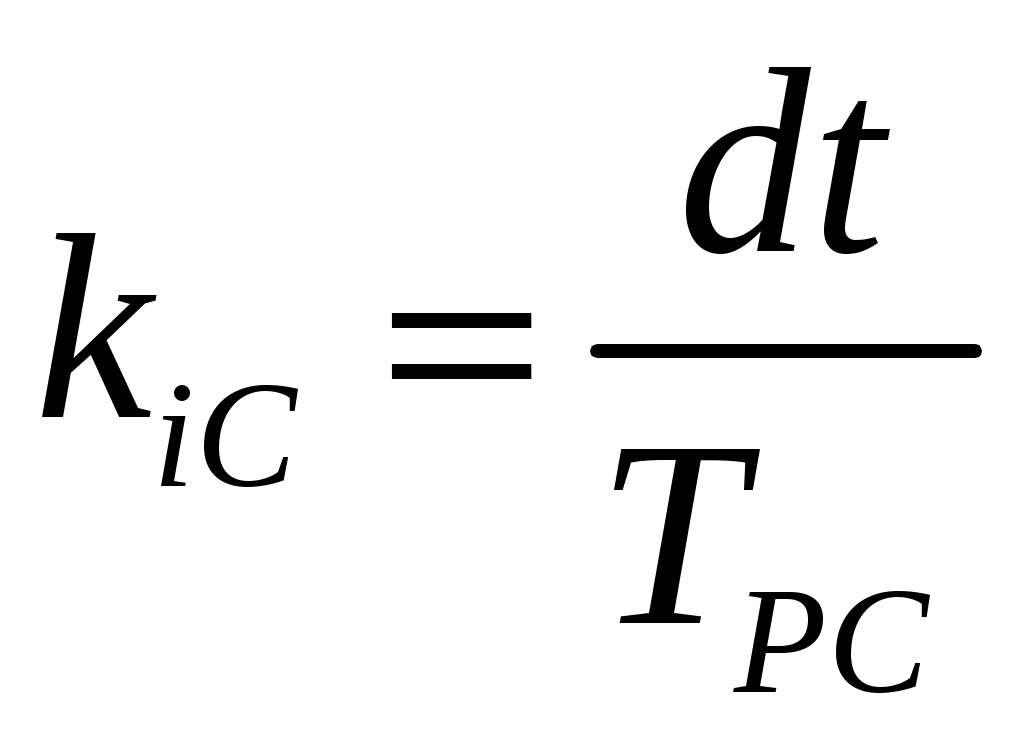, (17)

где dt = T_S – шаг расчета системы управления по времени.
Порядок выполнения работы и методические указания:

1. Получить от преподавателя задание на выполнение лабораторной работы, включающее № варианта параметров ДПТ.

2. Рассчитать параметры двигателя, коэффициенты ПИ-регулятора для контура тока и контура скорости (формулы для расчета представлены в разделе «Краткие теоретические сведения»).

---

3. Создать проект Models (рисунок 4).



Рисунок 4 – Создание нового проекта
4. Сохраняем под именем DCM_model (рисунок 5).



Рисунок 5 – Сохранение проекта
5. Создадим структуру объекта управления в библиотеке Models. Для этого переименуйте MAIN на DCM_model – формула будет содержать модель объекта регулирования – ДПТ и ПЧ.



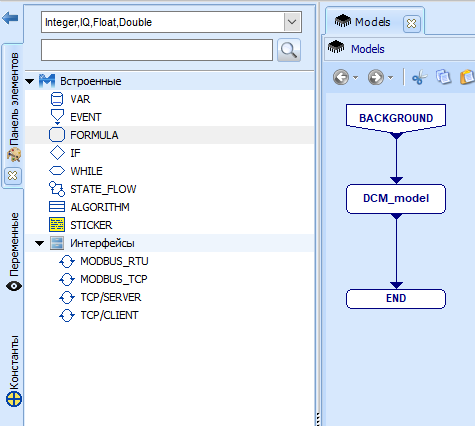
Рисунок 6 – Структура модели объекта управления в библиотеке Models
6. Параметры двигателя добавляем во вкладку «Константы». Для добавления новой константы во вкладке «Константы» необходимо нажать кнопку «Добавить». Создайте константы согласно рисунку 7, числовые значения для констант необходимо взять из варианта, либо рассчитать по предоставленным в теоретической сводке формулам.



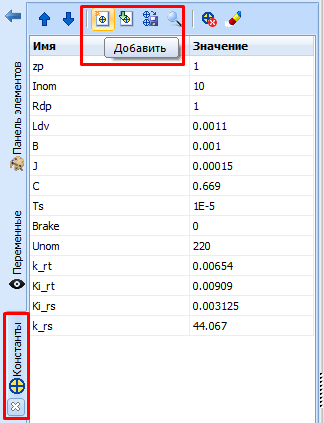
Рисунок 7 – Список используемых констант
7. Перейдите в формулу DCM_model. В панели элементов выберите следующие блоки и соедините, как показано на рисунке 8.

Название блока	Группа библиотеки	Графическое обозначение	Настройки
dMotor	Models\ Модели двигателей		In = Inom Rs = Rdp Ls = Ldv Zp = zp B = B J = J C = C остальные параметры задать = 0.
dDC_MOTOR	Models\ Модели двигателей		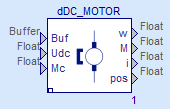SampleTime = Ts Brake = Brake
LABEL	Встроенные\ Вывод данных		Формат: Float
EDIT	Встроенные\ Ввод данных		Формат: Float Value = 24

---

Смотрите также файлы

• Рассказывание русской народной сказки Заяцхвастун иприсказки Начинаются наши сказки.docx

• Промышленные отходы и их переработка.rtf

• Если Вы любите экзотическую и необычную кухню, то торт Панчо Вилья.docx

• Контрольная работа 4 по теме Окружность и круг. Геометрические построения.docx

• Самарский государственный колледж сервисных технологий и дизайна.docx