ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 104
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Итегралы
24. Интеграл … равен …
| Интеграл | Ответ |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
| |  |
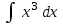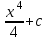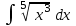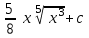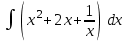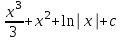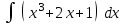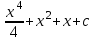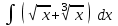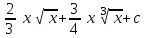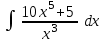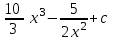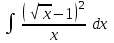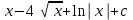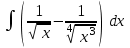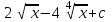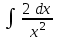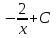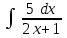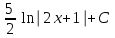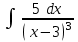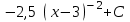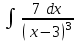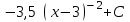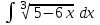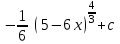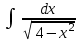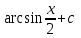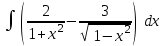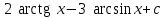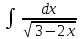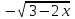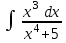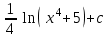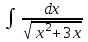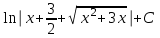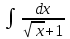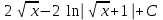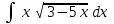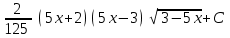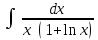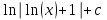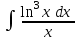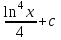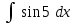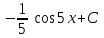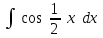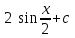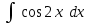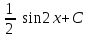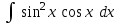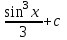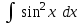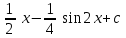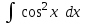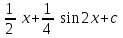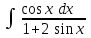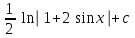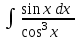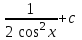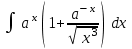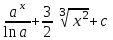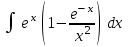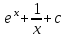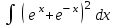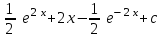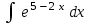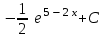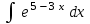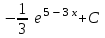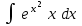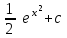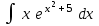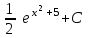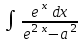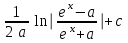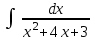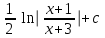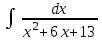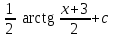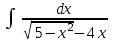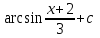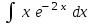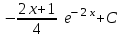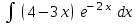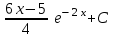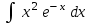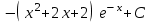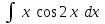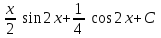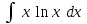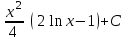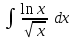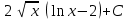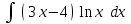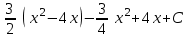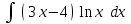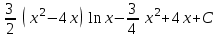| Определенные интегралы | |
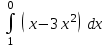 | 1/2 |
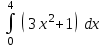 | 68 |
 |  |
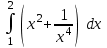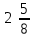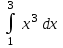 | 20 |
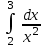 | 1/6 |
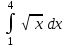 | 14/3 |
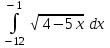 | 64 2/3 |
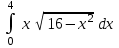 | 21 1/3 |
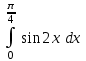 | 1/2 |
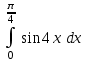 | 1/2 |
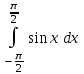 | 0 |
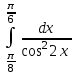 | (√3 – 1)/2 |
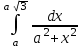 | /12a |
 |  |
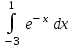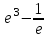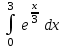 | 3 (e – 1) |
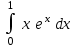 | 1 |
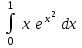 | (e – 1)/2 |
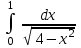 | п/6 |
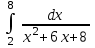 | 1/2 ln5/4 |
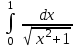 | ln|1 + √2| |
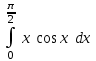 | п/2 – 1 |
 |  |
 |  |
| | |
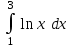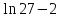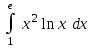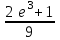44. Несобственный интеграл … равен …
| Несобственный интеграл | Ответ |
 | + ∞ |
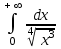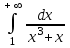 | 0,5 ln2 |
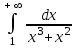 | 1 – ln2 |
 | + ∞ |
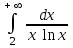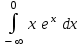 | -1 |
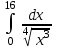 | 8 |
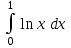 | -1 |
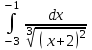 | 6 |
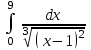 | 9 |
Пределы
51. Предел … равен …
| | |
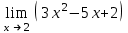 | 4 |
| на основании свойств пределов 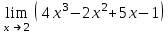 | 33 |
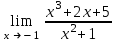 | 1 |
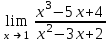 | 2 |
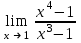 | 4/3 |
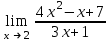 | 3 |
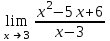 | 1 |
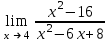 | 4 |
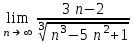 | 3 |
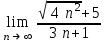 | 2/3 |
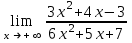 | 1/2 |
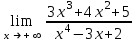 | 0 |
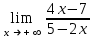 | -2 |
 | ∞ |
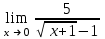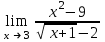 | 24 |
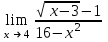 | -1/16 |
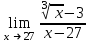 | 1/27 |
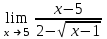 | -4 |
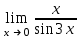 | 1/3 |
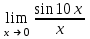 | 10 |
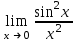 | 1 |
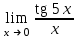 | 5 |
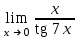 | 1/7 |
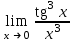 | 1 |
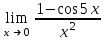 | 12,5 |
| Лопиталь 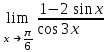 | √3/3 |
| Лопиталь 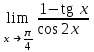 | 1 |
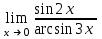 | 2/3 |
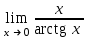 | 1 |
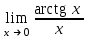 | 1 |
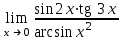 | 6 |
| Лопиталь 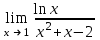 | 1/3 |
| Лопиталь 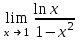 | -1/3 |
| Лопиталь 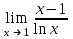 | 1 |
| Лопиталь 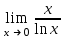 | 0 |
| Лопиталь 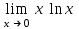 | 0 |
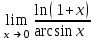 | 1 |
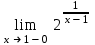 | 0 |
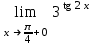 | 0 |
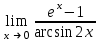 | 1/2 |
| Лопиталь 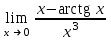 | 1/3 |
| Лопиталь 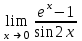 | 1/2 (или 0,5) |
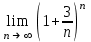 | e3 |
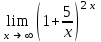 | e10 |
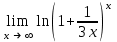 | 1/3 |
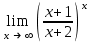 | e-1 |
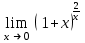 | e2 |
| Лопиталь  | ∞ |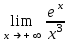
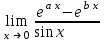 | a – b |
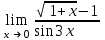 | 1/6 |
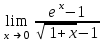 | 2 |
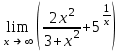 | 5/3 (правильного нет; правильный: = 3) |
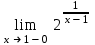| | 0 |
52. Предел … является вторым замечательным пределом.
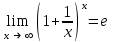
Предел … является первым замечательным пределом.
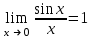
Производная функции
56. Производная функции … равна …
| где c и d – действительные числа  |  |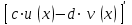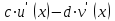
| где c и d – действительные числа  |  |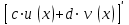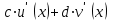
| где c – действительное число  |  |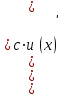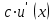
| где c – действительное число  |  |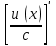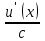
 |  |
 |  |
 |  |
 |  |
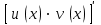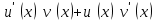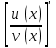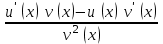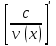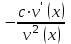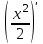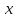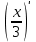 | 1/3 |
| y = c | 0 |
| y = x5 – 4x | 5x4 – 4 |
| y = log5(3x2 – 5) |  |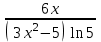
| y = ln32x |  |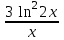
| y = (3x2 – 2x + 2)5 | 5 (6x – 2) (3x2 – 2x + 2)4 |
| y = 3x – lnx | 3 – 1 / x |
| y = x2 – sinx | 2x – cosx |
| y = x2 x sin2x | 2x sin2x + 2x2 cos2x |
| y = 53x | 3 · 53x ln5 |
| y = sin3x | 3 cos3x |
| y = cos25x | – 5 sin10x |
| y = xe2x | e2x + 2xe2x |
| y = tg3x | 3 sec23x |
| y = arcsin3x |  |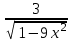
| y = arcctg5x |  |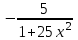
 |  |
 |  |
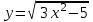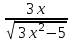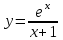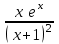| ey + x = y |  |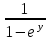
58. Производная функции ……….. при x = … равна …
| Функция__Производная'>Функция | Точка | Ответ |
| y = 3x2 – 5x + 2 | 1 | 1 |
| y = ln5x | 1 | 1 |
| y = xex | 0 | 1 |
| y = sin2x | п/2 | -2 |
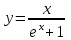 | 0 | 1/2 |
59. Производная функции xy2 = 4 в точке M0(1; 2) равна -1
71. Третья производная функции y = – ex равна … – ex
80. Частная производная по переменной x функции
z(x,y) = x3 – 3x2y + 2y3 составит …
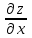= 3x2 – 6xyЧастная производная по переменной y функции
z(x,y) = x3 – 3x2y + 2y3 составит …
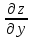= – 3x2 + 6y283. Четвертая производная функции y = 5x3 – 2x2 + 3x – 1 равна …0
8. Вторая производная функции y = 1/x равна … 2/x3
Вторая производная функции y = sin2x равна … -4 sin2x
9. Выберите правильный ответ на вопрос:
производная [c · u(x) – d · v(x)], где c и d – действительные числа, равна
| + c·u`(x) – d·v`(x) | c·u`(x) + d·v(x) | c`·u(x) – d`·v (x) | c·u`(x) + d·v`(x) | 0 |
16. Геометрически первая производная от функции, если она существует, есть