ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 105
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
тангенс угла наклона касательной к оси OX
35. Найдите вторую производную функции …
| Функция | Производная |
| y = sin2x | - 4 sin2x |
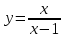 | 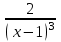 |
41. Найти производную y`x от функции, данной параметрически …
при t = …, где t Є [-∞; +∞].
| Функция | Точка t = | Ответ |
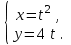 | 1 | 2 |
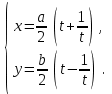 | 1 | 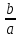 |
Б) Найти производную y`x от функции, заданной параметрически
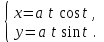 , где t Є [0; 2п].
, где t Є [0; 2п].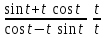 (или
(или 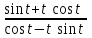 )
)В) Производная y`x от функции, заданной параметрически
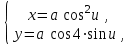
где u Є [0; 2п], равна …
- ctg2u
Г) Производная y`x от функции, заданной параметрически
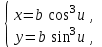
где u Є [0; 2п], равна … - tgu
Д) Производная y`x от функции, заданной параметрически
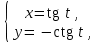
где t Є [0; 2п], равна …ctg2t
е) Производная y`x от функции, заданной параметрически
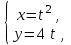
при t = 1, где t Є [-∞; +∞], равна …2
57. Производная функции xy + siny = 0, заданной неявно, в точке
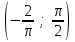 равна …
равна …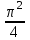
Площадь
4. Боковые стороны и меньшее основание трапеции равны по 10 см. Определить ее большее основание так, чтобы площадь трапеции была наибольшей
20 см
62. Решеткой длиной 120 м нужно огородить прилегающую к дому площадку наибольшей площади. Определить размеры прямоугольной площадки.
30 м; 60 м
40. Найти площадь плоской фигуры, ограниченной линиями … вокруг оси Ox.
| Линии | Ответ |
| y = sinx, x = /2, y = 0 | 2/4 (куб. ед.) или 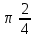 (куб. ед.) (куб. ед.) |
| y = √lnx, y = , x = e | (куб. ед.) |
| y = lnx, y = , x = e | 1 |
49. Площадь плоской фигуры, ограниченной линиями …, составляет …
| Линии | Площадь |
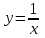 , x = 0, y = 2, y = 4 , x = 0, y = 2, y = 4 | ln2 кв. ед. |
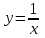 , , 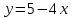 | (15/8 – ln4) кв. ед. |
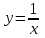 , , 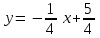 | (15/8 – ln4) кв. ед. |
| y = x2, x = 1, y = 0 | 1/3 кв. ед. |
| y2 = x, y = 4, x = 0 | 21 1/3 (кв. ед.) |
| x = y2, y = – x + 2 | 4,5 (кв. ед.) |
| x = y2, y = x | 1/6 (кв. ед.) |
| x = y2, x = 4 | 10 2/3 (кв. ед.) |
| y = x2 – 9, y = 0 | 36 кв. ед. |
| y = x2 – 2x + 1, y = 1 | 4/3 (кв. ед.) |
| y = x2 – 4x + 5, y = 5 | 10 2/3 (кв. ед.) |
| y = sinx, y = cosx, x = 0, x = п/4 | (√2 – 1) (кв. ед.) |
| y = sinx, x = 0, x = , y = 0 | 1 (кв. ед.) |
| x = √y, y = 0, x = 1 | 1/3 кв. ед. |
| x = √y + 2, y = 0, x = 6 | 21 1/3 (кв. ед.) |
Точка разрыва
68. Точками разрыва заданной функции … являются
| Функция | Точки разрыва |
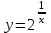 | 0 |
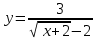 | 2 |
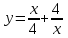 | 0 |
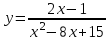 | 3, 5 |
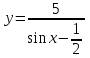 | 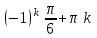 |
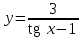 | 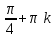 |
69. Точками разрыва функции y = tgx на промежутке [0; п] является
п/2
Точкой разрыва функции y = tgx на промежутке [0; п] является
п/2
72. У заданной функции y = 4/x + x/4 … точкой разрыва является 0
Дифференциалы
70. Третий дифференциал функции y = 3x2 – 5x + 2 равен … 0
-
Второй дифференциал функции y = sin x равен … - sinx dx2
-
Второй дифференциал функции y = cos x равен … - cosx dx2
18. Дифференциал функции … равен …
| Интеграл | Ответ |
| y = x3 + 3x2 + 3x | (3x2 + 6x + 3) dx |
| y = (ax2 – b)3 | 4ax(ax2 – b) dx |
| y = ln2x | 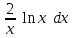 |
| y = sin22x | 2 sin4x dx |
19. Дифференциал функции y = x3 при x = 1 и x = 0,1 равен … 0,3
22. а) Заменив приращение функции дифференциалом, приближенно найти
sin31°.
0,515
Б) Заменив приращение функции дифференциалом, приближенно найти
arctg 1,05.
0,81
Асимптоты
6. Вертикальными асимптотами графика функции … являются …
| | |
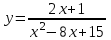 | x = 3; x = 5 |
| y = lnx | x = 0 |
| y = 2/x + x/2 | x = 0 |
17. Горизонтальной асимптотой графика функции y = ax является y = 0
43. Наклонной асимптотой графика функции y = x3 / (x2 – 3) является
y = x
Приращение функции, нормаль
15. Вычислить приближенно приращение функции y = x2 + 2x + 3, когда x изменяется от 2 до 1,98.
-0,12
22. а) Заменив приращение функции дифференциалом, приближенно найти
sin31°.
0,515
Б) Заменив приращение функции дифференциалом, приближенно найти
arctg 1,05.
0,81
-
Приращенное значение функции y = x2 при x = 0,5 в т. x = 3 равно
12,25
45. Нормаль к графику функции y = x2 в точке M0(1; 1) определяется уравнением
y = – 1/2 x + 3/2
б) Нормаль к графику функции y = ex в точке M0(0; 1) определяется уравнением
y = – x + 1
Интервалы
25. Интервалы вогнутости функции
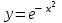 можно найти как …
можно найти как …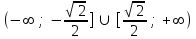
Интервалы выпуклости функции y = x3/3 – 3x2 + 5x + 1 можно найти как
(– ∞; 3)
26. Интервалы монотонного возрастания функции … равны …
| Функция | Интервал |
| y = 6x2 – 3x | (1/4; + ∞) |
| y = x3 – 3x2 | (– ∞; 0] U [2; + ∞) |
| y = x/4 + 4/x | (– ∞; – 4] U [4; + ∞) |
| y = x3 – 6x2 + 9x + 3 | (– ∞; 1] U [3; + ∞) |
Интервалы монотонного убывания функции … равны …
| Функция | Интервал |
| y = 3x2 – 12x + 2 | (– ∞; 2) |
| y = x3 – 12x | (-2; 2) |
| y = x3 – 3x2 | (0; 2) |
| y = x3 + 3x2 + 3x + 4 | 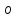 |
 | (– 4; 0] U [0; 4) |
37. Найти интервалы монотонного возрастания функции y = 6x2 – 3x.
(1/4; +∞)
Экстремумы функции
73. Функция … имеет экстремум (максимум или минимум) при x, равном…
| Функция | Экстремум |
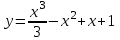 | 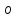 |
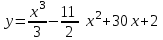 | 5; 6 |
 | -4; 4 |
84. Экстремум функции z(x, y) = x6 + y6 составляет …
z(0, 0) = 0
Экстремум функции z(x, y) = x3 + y3 – 9xy составляет …
z(3, 3) = -27
Значение и область определения функции
33. Наибольшим значением функции
А) y = x2 – 2x на отрезке [-1; 1] является … 3
Б) Наибольшим значением функции y = – x2 + 2x на отрезке [-1; 2] является …1
53. Приближенное значение выражения (1,02)4,05 составляет … 1,08
-
Приближенное значение выражения (1,02)3 (0,97)2 составляет …1
-
Приближенное значение выражения √(8,04)2 + (6,03)2 составляет 10,05