Файл: пензенский государственный университет политехнический институт.docx
Добавлен: 30.11.2023
Просмотров: 216
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Основные положения, выносимые на защиту:
Эквивалентные преобразования моделей задач линейного программирования
Анализ моделей и алгоритмов решения задач о назначениях
Анализ эквивалентных преобразований моделей задач о назначениях
Модель и алгоритм решения задачи с приоритетными назначениями
В большинстве случаев целевые функции
f1(X), f2 (X),..., fk(X)
многокритериальной задачи о назначениях взаимно конфликтуют в том смысле, что улучшения значений одних функций можно добиться только за счет ухудшения значений других. Например, высокая функциональность и надежность информационной системы обеспечивается увеличением затрат на производство и эксплуатацию. В результате одно решение может превосходить другое по одним частным критериям, уступая при этом ему по другим.
Для сравнения критериальных векторов в многокритериальных задачах вводят отношение доминирования. Задача о назначениях в классической постановке является задачей минимизации. В случае задачи минимизации
говорят, что критериальный вектор
F(X1) ( f1(X1), f2 (X1),..., fk(X1))
доминирует по Парето вектор F(X2 ) ( f1(X2 ), f2 (X2 ),..., fk(X2 )) и
p
обозначают F(X1) F(X2 ) , если fl(X1)
fl(X2 )
для всех
l 1, k, при этом
хотя бы для одного индекса lвыполняется
fl(X1)
fl(X2 ) . Критериальный
вектор F(X0 ) называется оптимальным по Парето, если
p
{F(X) | F(X) F(X0 ), X D
} . Такой вектор называется также недоминируемым по Парето. Множество критериальных векторов, оптимальных по Парето, называют множеством Парето в критериальном
пространстве или фронтом Парето и обозначают F(P) .
Доминирование по Парето, определенное для пар критериальных векторов, порождает соответствующее отношение на множестве допустимых
решений Dмногокритериальной задачи о назначениях. Пусть тогда
X1, X2 D,
pp
X1 X2 F(X1) F( X2 ) .
Решение X0 Dназывается оптимальным по Парето, если
p
{X D| F(X) F( X0 )} . Таким образом, решение оптимально по Парето тогда и только тогда, когда оно является прообразом недоминируемого критериального вектора. Множество всех оптимальных по Парето решений
задачи называют множеством Парето и обозначают P(D) .
Решением многокритериальной задачи обычно считают либо единственный оптимальный по Парето вектор, либо приближение множества Парето конечным числом векторов. Первую постановку принято называть локальной многокритериальной задачей, вторую – глобальной. Выбор окончательного решения осуществляется, как правило, лицом, принимающим решения (ЛПР).
Алгоритм решения простейшей линейной многокритериальной задачи о назначениях
Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при
скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.
В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.
Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует
предварительного нормирования матриц затрат
Сl,
l 1, k, т.е. приведения
их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.
Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75).
-
Нормировать матрицы затрат Сl, l 1, k:
cl cl
сl ijmin .
c
c
ijl
max
l
min
-
Составить целевые функции безразмерными коэффициентами:
f1(X), f2 (X),..., fk(X) с
n nl
fl(X) сijxij, l 1, k
i1 j1
-
Составить вектор
(1, 2,..., k)
весовых коэффициентов
относительной важности целевых функций
f1(X), f2 (X),..., fk(X) ,
l 0 ,
l 1.k,
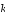
l 1. В том случае, если все критерии имеют одинаковую
l1
важность,
l 1, l 1.k.
-
Составить скалярную целевую функция (обобщенный критерий)
g(X) ) ,
( f1(X), f2 (X),..., fk(X),
где – оператор свертки.
-
Перейти к однокритериальной задаче о назначениях вида
g(X) min,
(76)
n
xij 1, j 1, n,
i1
(77)
n
xij 1, i 1, n,
j1
(78)
xij{0,1}, i, j 1, n.
(79)
-
Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений.
Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки.
-
1 ... 8 9 10 11 12 13 14 15 ... 21
Алгоритм решения простейшей линейной многокритериальной задачи о назначениях
Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при
скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.
В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.
Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует
предварительного нормирования матриц затрат
Сl,
l 1, k, т.е. приведения
их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.
Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75).
-
Нормировать матрицы затрат Сl, l 1, k:
cl cl
сl ijmin .
c
c
ijl
max
l
min
-
Составить целевые функции безразмерными коэффициентами:
f1(X), f2 (X),..., fk(X) с
n nl
fl(X) сijxij, l 1, k
i1 j1
-
Составить вектор
(1, 2,..., k)
весовых коэффициентов
относительной важности целевых функций
f1(X), f2 (X),..., fk(X) ,
l 0 ,
l 1.k,
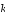
l 1. В том случае, если все критерии имеют одинаковую
l1
важность,
l 1, l 1.k.
-
Составить скалярную целевую функция (обобщенный критерий)
g(X) ) ,
( f1(X), f2 (X),..., fk(X),
где – оператор свертки.
-
Перейти к однокритериальной задаче о назначениях вида
g(X) min,
(76)
n
xij 1, j 1, n,
i1
(77)
n
xij 1, i 1, n,
j1
(78)
xij{0,1}, i, j 1, n.
(79)
-
Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений.
Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки.
-
1 ... 8 9 10 11 12 13 14 15 ... 21
Алгоритм решения простейшей линейной многокритериальной задачи о назначениях
Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при
скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.
В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.
Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует
предварительного нормирования матриц затрат
Сl,
l 1, k, т.е. приведения
их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.
Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75).
-
Нормировать матрицы затрат Сl, l 1, k:
cl cl
сl ijmin .
c
c
ijl
max
l
min
-
Составить целевые функции безразмерными коэффициентами:
f1(X), f2 (X),..., fk(X) с
n nl
fl(X) сijxij, l 1, k
i1 j1
-
Составить вектор
(1, 2,..., k)
весовых коэффициентов
относительной важности целевых функций
f1(X), f2 (X),..., fk(X) ,
l 0 ,
l 1.k,
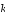
l 1. В том случае, если все критерии имеют одинаковую
l1
важность,
l 1, l 1.k.
-
Составить скалярную целевую функция (обобщенный критерий)
g(X) ) ,
( f1(X), f2 (X),..., fk(X),
где – оператор свертки.
-
Перейти к однокритериальной задаче о назначениях вида
g(X) min,
(76)
n
xij 1, j 1, n,
i1
(77)
n
xij 1, i 1, n,
j1
(78)
xij{0,1}, i, j 1, n.
(79)
-
Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений.
Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки.
-
1 ... 8 9 10 11 12 13 14 15 ... 21
Алгоритм решения простейшей линейной многокритериальной задачи о назначениях
Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при
скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.
В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.
Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует
предварительного нормирования матриц затрат
Сl,
l 1, k, т.е. приведения
их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.
Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75).
-
Нормировать матрицы затрат Сl, l 1, k:
cl cl
сl ijmin .
c
c
ijl
max
l
min
-
Составить целевые функции безразмерными коэффициентами:
f1(X), f2 (X),..., fk(X) с
n nl
fl(X) сijxij, l 1, k
i1 j1
-
Составить вектор
(1, 2,..., k)
весовых коэффициентов
относительной важности целевых функций
f1(X), f2 (X),..., fk(X) ,
l 0 ,
l 1.k,
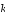
l 1. В том случае, если все критерии имеют одинаковую
l1
важность,
l 1, l 1.k.
-
Составить скалярную целевую функция (обобщенный критерий)
g(X) ) ,
( f1(X), f2 (X),..., fk(X),
где – оператор свертки.
-
Перейти к однокритериальной задаче о назначениях вида
g(X) min,
(76)
n
xij 1, j 1, n,
i1
(77)
n
xij 1, i 1, n,
j1
(78)
xij{0,1}, i, j 1, n.
(79)
-
Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений.
Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки.
-
1 ... 8 9 10 11 12 13 14 15 ... 21
Алгоритм решения простейшей линейной многокритериальной задачи о назначениях
Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при
скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.
В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.
Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует
предварительного нормирования матриц затрат
Сl,
l 1, k, т.е. приведения
их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.
Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75).
-
Нормировать матрицы затрат Сl, l 1, k:
cl cl
сl ijmin .
c
c
ijl
max
l
min
-
Составить целевые функции безразмерными коэффициентами:
f1(X), f2 (X),..., fk(X) с
n nl
fl(X) сijxij, l 1, k
i1 j1
-
Составить вектор
(1, 2,..., k)
весовых коэффициентов
относительной важности целевых функций
f1(X), f2 (X),..., fk(X) ,
l 0 ,
l 1.k,
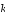
l 1. В том случае, если все критерии имеют одинаковую
l1
важность,
l 1, l 1.k.
-
Составить скалярную целевую функция (обобщенный критерий)
g(X) ) ,
( f1(X), f2 (X),..., fk(X),
где – оператор свертки.
-
Перейти к однокритериальной задаче о назначениях вида
g(X) min,
(76)
n
xij 1, j 1, n,
i1
(77)
n
xij 1, i 1, n,
j1
(78)
xij{0,1}, i, j 1, n.
(79)
-
Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений.
Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки.
-
1 ... 8 9 10 11 12 13 14 15 ... 21
предварительного нормирования матриц затрат
Сl,
l 1, k, т.е. приведения
их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.
Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75).
-
Нормировать матрицы затрат Сl, l 1, k:
cl cl
сl ijmin .
c
c
ijl
max
l
min
-
Составить целевые функции безразмерными коэффициентами:
f1(X), f2 (X),..., fk(X) с
n nl
fl(X) сijxij, l 1, k
i1 j1
-
Составить вектор
(1, 2,..., k)
весовых коэффициентов
относительной важности целевых функций
f1(X), f2 (X),..., fk(X) ,
l 0 ,
l 1.k,
l 1. В том случае, если все критерии имеют одинаковую
l1
важность,
l 1, l 1.k.
-
Составить скалярную целевую функция (обобщенный критерий)
g(X) ) ,
( f1(X), f2 (X),..., fk(X),
где – оператор свертки.
-
Перейти к однокритериальной задаче о назначениях вида
| g(X) min, | (76) |
| n xij 1, j 1, n, i1 | (77) |
| n xij 1, i 1, n, j1 | (78) |
| xij{0,1}, i, j 1, n. | (79) |
-
Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений.
Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки.
- 1 ... 8 9 10 11 12 13 14 15 ... 21
Решение простейшей линейной многокритериальной задачи о назначениях с использованием линейной свертки
Обобщенный критерий, построенный с использованием оператора линейной свертки, имеет вид:
k
g(X)
,
lfl(X)
i1
Решение простейшей линейной многокритериальной задачи о назначениях с использованием линейной свертки
Обобщенный критерий, построенный с использованием оператора линейной свертки, имеет вид:
k
g(X)
,
lfl(X)
i1
Решение простейшей линейной многокритериальной задачи о назначениях с использованием линейной свертки
Обобщенный критерий, построенный с использованием оператора линейной свертки, имеет вид:
k
g(X)
где
fi(X) – целевые функции с нормированными коэффициентами, l 1.k;
l– весовые коэффициенты,
l 1.k.
По своему смыслу линейная свертка представляет собой среднее взвешенное частных критериев и именно с этих позиций во многих случаях ее использование в многокритериальных задачах о назначениях представляется обоснованным. Результатом применения линейной свертки является получение решения, оптимального по Парето. Текст программы для нахождения решения простейшей многокритериальной линейной задачи о назначениях методом линейной свертки критериев в среде «Mathcad» приведен в листинге 3.
Листинг 3 – Решение многокритериальной линейной задачи о назначениях с использованием линейной свертки

Пусть дана многокритериальная задача о назначениях вида (70) – (75). Матрицы затрат задачи и вектор весовых коэффициентов относительной важности целевых функций представлены на рисунке 16:

Рисунок 16 – Исходные данные простейшей линейной многокритериальной задачи о назначениях
Программа находит оптимальное по Парето решение, а также значения соответствующего ему критериального вектора (рисунок 17):

Рисунок 17 – Результаты решения многокритериальной задачи о назначениях с использованием линейной свертки
Решая задачу многократно с изменением весовых коэффициентов, можно сгенерировать множество точек, оптимальных по Парето (рисунок 18):

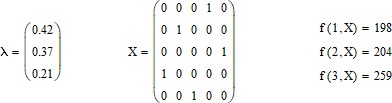
Рисунок 18 – Результаты решения многокритериальной задачи о назначениях с различными векторами весовых коэффициентов
Оптимизации многокритериальной задачи о назначениях с использованием оператора линейной свертки присущ ряд недостатков:
-
субъективный характер выбора весовых коэффициентов и общая, как следствие, субъективность получаемых решений; -
низкие значения одних целевым функциям (вплоть до нулевого) могут компенсироваться высокими значениями других целевым функциям, поэтому полученное решение, оптимальное в смысле обобщенного критерия, может характеризоваться низкими значениями по ряду частных критериев и быть по этой причине неприемлемым для ЛПР; -
чувствительность решения к изменению параметров исходной модели (например, малым приращениям весовых коэффициентов могут соответствовать большие приращения значений целевых функций).
Следует отметить, что вышеперечисленные недостатки могут быть скорректированы ЛПР.
-
Решение простейшей линейной многокритериальной задачи о назначениях с использованием мультипликативной свертки
Обобщенный критерий, построенный с использованием оператора мультипликативной свертки, имеет вид:
k
g(X)
l1
fi(X)
l .
где
fi(X)
– целевые функции с нормированными коэффициентами, l 1.k;