Файл: пензенский государственный университет политехнический институт.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Диссертация

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 213

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Содержание

Введение

Основные положения, выносимые на защиту:

Эквивалентные преобразования моделей задач линейного программирования

Анализ моделей и алгоритмов решения задач о назначениях

Анализ эквивалентных преобразований моделей задач о назначениях

Выводы

Модель и алгоритм решения задачи с приоритетными назначениями

Выводы

Алгоритм решения простейшей линейной многокритериальной задачи о назначениях Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует предварительного нормирования матриц затратСl,l 1, k, т.е. приведения их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75). Нормировать матрицы затрат Сl, l 1, k: cl clсl ijmin . c  cijl maxlmin Составить целевые функции безразмерными коэффициентами: f1(X), f2 (X),..., fk(X) с n nlfl(X)  сijxij, l 1, ki1 j1 Составить вектор   (1, 2,..., k)весовых коэффициентов относительной важности целевых функцийf1(X), f2 (X),..., fk(X) ,l 0 , l 1.k, l 1. В том случае, если все критерии имеют одинаковуюl1 важность,l 1, l 1.k. Составить скалярную целевую функция (обобщенный критерий) g(X)   ) ,( f1(X), f2 (X),..., fk(X),где  – оператор свертки. Перейти к однокритериальной задаче о назначениях вида g(X)  min, (76) n xij 1, j 1, n,i1 (77) n xij 1, i 1, n,j1 (78) xij{0,1}, i, j 1, n. (79) Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений. Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки. 1   ...   8   9   10   11   12   13   14   15   ...   21

Решение простейшей линейной многокритериальной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки Под идеальной точкой в многокритериальной задаче о назначениях вида (71) – (76) понимают такой векторF*(X)  Rk, компоненты которого являются минимумами целевых функцийf1(X), f2 (X),..., fk(X) по отдельности, т.е.fl*(X)  min fl(X),XDl 1, k. В практических задачах идеальная точка является недостижимой [73]. Свертка на основе идеальной точкиF*(X)имеет вид: g(X)  (F(X), F*(X)) , где  – некоторая метрика вRk. Наиболее часто используются взвешенная чебышевская метрика g(X)  maxlfl(X)  fl* l (80) и взвешенная евклидова метрика kg(X)  ( fl(X)  fl*)2.l1 (81) Предлагается следующий алгоритм составления обобщенного скалярного критерия на основе идеальной точки: составить kоднокритериальных задач о назначениях вида n nlfl(X)  cijxij min,i1 j1n (82)  xij 1, j 1, n,i1n (83)  xij 1, i  1, n,j1 (84) xij{0,1}, i, j 1, n, (85) гдеl 1,k; найти X * – оптимальное решение l-й задачи вида (82) – (84) и lfl*  fl(X*) , l 1, k; lсоставить вектор F*(X)  ( f*, f*,..., f*) , гдеfl*  fl(X*) , l 1, k;1 2 k lсоставить свертку на основе отклонения от идеальной точки по формуле (80) или (81). Разработана программа для нахождения решения многокритериальной линейной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки средствами математического пакета Mathcad, полный текст которой представлен в приложении E. На рисунке 20 приведены результаты применения свертки на основе отклонения от идеальной точки к многокритериальной задаче о назначениях, исходные данные которой совпадают с исходными данными задачи, решенной с использованием линейной свертки: Рисунок 20 – Результаты решения многокритериальной линейной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки На рисунке 20 представлены матрица X – оптимальное по Парето решение, полученное с использованием чебышевской метрики, и матрица Y – оптимальное по Парето решение, полученное с использованием евклидовой метрики. Также программа находит для каждого оптимального по Парето решения значения соответствующего ему критериального вектора. Применяя алгоритм многократно с изменением весовых коэффициентов, можно построить множество точек Парето. Выбор конкретного решения из множества Парето-оптимальных осуществляется ЛПР.Следует отметить, что в некоторых прикладных задачах ЛПР за идеальную точку может принять реальное решение, соответствующее некоторым принятым стандартам или планируемым значениям. 1   ...   10   11   12   13   14   15   16   17   ...   21

Модель и алгоритм решения многокритериальной задачи о назначениях с целевыми функциями противоположного направления

Модель и алгоритм решения многокритериальной открытой задачи о назначениях Обобщим открытую задачу о назначениях на случай многокритериальности. Математическая модель такой задачи в предположенииm nимеет вид:

Модель и алгоритм решения многокритериальной задачи с порядком назначений Обобщим задачу с порядком назначений на случай многокритериальности. Математическая модель такой задачи имеет вид:nn f1(X)  c1 x min,(121) ijiji1 j1… nn k(X)  ckx min,n (122)  xij 1,n j 1, n, (123)  xij 1, i  1, n, (124) {0,1}, i1, n, j 1, n, , i1, n, j h1, n, j*  1, h. (126) f xij гдеP {1,2,.., h}пр.(i, j)  (i, j*)– подмножество индексов работ, распределяемых в первую очередь.В главе 2 показано, что однокритериальная задача с порядком назначений эквивалента совокупности двух последовательно решаемых задач – открытой и с недопустимыми назначениями. Аналогично, многокритериальная задача с порядком назначений эквивалента совокупности двух последовательно решаемых задач – многокритериальной открытой задаче и многокритериальной задаче с недопустимыми назначениями. Следовательно, можно описать алгоритм решения многокритериальной задачи с порядком назначений. Нормировать матрицы затрат Сl, l 1, k: cl clсl ijmin . c  cijl maxlmin Найти размер штрафа Ml 2n. Построить математическую модель назначения на работы из множества P :

Выводы

Заключение

Список использованных источников



Зная оптимальное решение

Y* ( y* )

ij

задачи (53) – (56) и оптимальное


решение

Z* (z* )

ij

задачи (57) – (60), можно найти оптимальное решение


X* задачи (48) – (52):

y* , i 1, n, j 1, k;

x* ij

ijz* , i 1, n, j k1, n.

ij

Таким образом, задачи с порядком назначений (48) – (52) эквивалентна совокупности двух последовательно решаемых задач – открытой задаче и задаче с недопустимыми назначениями. Для каждой из этих задач существует эквивалентная простейшая модель. Следовательно, задача с порядком назначений (48) – (52) эквивалентна совокупности двух

последовательно решаемых простейших линейных задач – задаче (53) – (56) и задаче (57) – (60).

Эквивалентное преобразование задачи с порядком назначений в совокупность двух последовательно решаемых простейших линейных задач формулируется так:

  1. построить задачу (53) – (56);

  2. решить задачу (53) – (56) венгерским методом или методом Мака,




найти оптимальное решение

Y* ( y* ) ;

ij




  1. построить задачу (57) – (60).

Таким образом, можно сформулировать алгоритм решения задачи о назначениях (48) – (52) .

  1. Применить эквивалентное преобразование задачи с порядком назначений в совокупность двух последовательно решаемых простейших линейных задач.

  2. Решить задачу (57) – (60) венгерским методом или методом




Мака. Найти оптимальное решение

Z* (z* ) .

ij




  1. Найти оптимальное решение X* задачи (48) – (52):

y* , i 1, n, j 1, k;

x* ij

ijz* , i 1, n, j k1, n.

ij

Разработана программа поиска оптимального решения задачи с порядком назначений средствами математического пакета «Mathcad» (приложение Г). Исходные данные задачи (рисунок 11) формируются случайным образом.



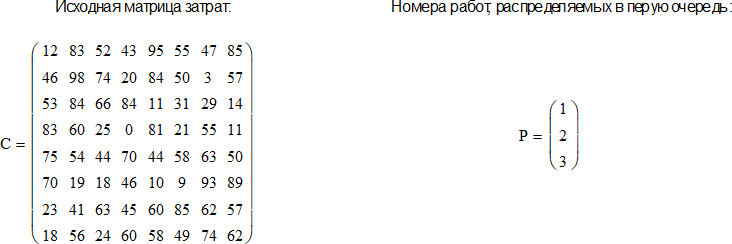
Рисунок 11 – Исходные данные задачи с порядком назначений



На рисунке 12 представлены результаты работы программы.


Рисунок 12 – Результаты поиска оптимального решения задачи с порядком назначений
При заданной матрице затрат и установленном порядке назначений целевая функция задачи достигает минимального значения, равного 128.

Следует отметить, что необходимость учета порядка назначений в общем случае приводит к росту значений целевой функции. Ниже представлено решение простейшей линейной задачи о назначениях, матрица затрат С которой совпадает с матрицей затрат задачи с порядком назначений (рисунок 13).


Рисунок 13 – Результаты поиска оптимального решения простейшей линейной задачи с матрицей затрат С
Как видно, при одинаковой матрице затрат минимальное значение целевой функции простейшей линейной задачи о назначениях меньше минимального значения целевой функции задачи порядком назначений.

    1. 1   ...   5   6   7   8   9   10   11   12   ...   21

Модель и алгоритм решения задачи с приоритетными назначениями


Добавим к простейшей линейной задаче (1) – (4) дополнительное требование. Будем полагать, что некоторые назначения имеют приоритет перед другими. Данная ситуация имеет место, когда для некоторых работ выделен предпочтительный состав исполнителей. Примером также является случай, когда исполнители имеют свои предпочтения по выбору работы, которые желательно учесть [70].

Пусть имеется nработ и nисполнителей. Известны трудовые затраты

cij

на выполнение i-м исполнителем j-й работы ( i 1,n,

j 1, n). Каждый


исполнитель может быть назначен только на одну работу, каждая работа может быть выполнена только одним исполнителем, при этом некоторые

назначения имеют приоритет перед другими. Требуется распределить работы так, чтобы они были исполнены с минимальными затратами и с учетом приоритетности назначений.

На множестве

приоритета

I {1,2,.., n}

индексов установим бинарное отношение

Rпр. {(i, j) | назначение (i, j)

имеет приоритет}.

Пары

(i, j) Rпр.

подлежат распределению назначений в первую



очередь. Обозначим отношение порядка распределения назначений через

пр.

.

Тогда математическая модель задачи с недопустимыми комбинациями назначений принимает вид:

nn

f(X) cijxij min,

i1 j1
n
(61)

xij 1, j 1, n,

i1

n
(62)

xij 1, i1, n,

j1
(63)

xij{0,1}, i1, n, j 1, n,
(64)

пр.

(i, j) (i*, j*) , (i*, j*) Rпр.
(65)





Rпр.

Введем в рассмотрение матрицу затрат таким образом:

Qnn, связанную с отношением


где M– штраф.

qij

cij, если (i, j) Rпр.,



cijM, если (i, j)  Rпр.,

Введение матрицы Q обосновано следующими соображениями. Классические методы решения задачи о назначениях основаны на идее выбора в каждой строке матрицы затрат минимального элемента.

Неизвестная

xij, такая, что

(i, j) Rпр. , будет «штрафоваться» путем ввода в

целевую функцию выражения

(сij M)xij, что обеспечит учет

приоритетности выделенных назначений. Вместе с тем очевидно, что положения оптимального выбора среди назначений, не имеющих приоритета, не изменятся, если к каждому элементу матрицы затрат добавить одно и то

же число. Для определенности будем полагать

M 2n max сij.


Эквивалентное преобразование задачи с приоритетными назначениями в простейшую линейную задачу формулируется так:

  1. найти размер штрафа

M 2n max сij;

Смотрите также файлы