Файл: Научноисследовательская работа по дисциплине Механика деформируемого твёрдого тела.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 48

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГАОУ ВО «КАЗАНСКИЙ (ПРИВОЛЖСКИЙ)

ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

НАБЕРЕЖНОЧЕЛНИНСКИЙ ИНСТИТУТ (ФИЛИАЛ)

Исследование несущей способности шарнирно-стержневой системы

Научно-исследовательская работа

по дисциплине «Механика деформируемого твёрдого тела»

Учебно-методическое пособие для аспирантов направления подготовки 01.06.01. Математика и механика. Направленность (профиль) подготовки 01.02.04. Механика деформируемого твёрдого тела;

для магистрантов, обучающихся по направлению подготовки 08.04.01. Строительство

Набережные Челны

2020

Исследование несущей способности шарнирно-стержневой системы. Научно-исследовательская работа по дисциплине «Механика деформируемого твёрдого тела». Учебно-методическое пособие для аспирантов направления подготовки 01.06.01. Математика и механика. Направленность (профиль) подготовки 01.02.04. Механика деформируемого твёрдого тела; для магистрантов, обучающихся по направлению подготовки 08.04.01. Строительство / Э. С. Сибгатуллин, К. Э. Сибгатуллин, М. Э. Сибгатуллин –Набережные Челны: НЧИ КФУ, 2020, 36 с.

Учебно-методическое пособие по выполнению научно-исследовательской работы разработано в соответствии с требованиями ФГОС высшего образования к уровню подготовки выпускника по направлению подготовки 01.06.01 «Математика и механика», 08.04.01 «Строительство». Излагаются теоретический материал, пример расчёта и задание для самостоятельной работы.

Рецензенты: д-р физ.-матем. наук, профессор Н. С. Габбасов, ФГАОУ ВО «Казанский федеральный государственный университет»

канд. техн. наук, доцент К. Ф. Исламов, ФГАОУ ВО «Казанский федеральный государственный университет»

Печатается в соответствии с решением научно-методического совета Набережночелнинского института КФУ.

© Набережночелнинский институт КФУ, 2020 год

1. Задание для самостоятельной НИР студента (аспиранта)


Бесконечно жесткий брус шарнирно подвешен на трех вертикальных стержнях (рис. 1). Определить предельную несущую способность системы. Исходные данные задачи взять из таблицы 1, согласно индивидуальному шифру студента. Индивидуальный шифр студента (аспиранта) совпадает с последними четырьмя цифрами номера его зачетной книжки либо может быть назначен преподавателем. Под этими цифрами нужно написать буквы А, Б, В, Г. Буква и соответствующая цифра определяют координаты личных исходных данных в табл. 1. Например, для шифра 9156 исходные данные в табл. 1 выделены. В табл. 1 расстояния и длины стержней даны в метрах, площади поперечных сечений стержней 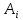– в 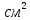, пределы текучести материалов стержней 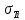– в ГПа (i=1, 2, 3). Задачу необходимо решить с использованием кинематического и статического методов теории предельного равновесия (см. пример решения). Рассмотреть шесть вариантов задачи, варьируя между собой заданные площади поперечных сечений стержней. Результаты расчетов оформить в виде следующей таблицы 2 (например, для шифра 9156):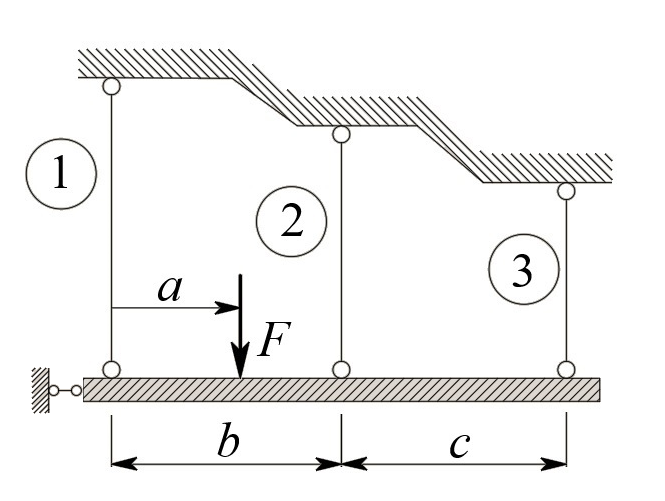



Рис. 1.

Таблица 1

Вар.
a
b
c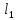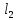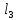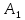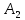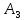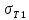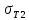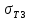


















0
1
3
4
2
1.5
1
3
4
5
0,2
0,25
0,3

1
2
4
3
3
2.5
2
1
3
4
0,3
0,2
0,25

2
3
4
5
2.5
2
3
8
2
3
0,4
0,2
0,3

3
6
5
4
1.5
2
4
3
1
2
0,5
0,3
0,4

4
4
3.5
4.5
3.5
4
4
3
1
8
0,2
0,4
0,3

5
3
4.5
3.5
4
3
3
7
2
4
0,3
0,2
0,4

6
5
4.5
5.5
4.5
5
2
1
3
5
0,5
0,2
0,3

7
6
5.5
4.5
5
2
1
2
4
6
0,3
0,5
0,2

8
4
2
4
3
4
2
1
3
7
0,6
0,4
0,3

9
3
4
2
3
3
3
7
2
8
0,4
0,6
0,4




A
Б
В
Г

Таблица 2

№










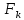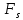V

1
7
2
4









2
7
4
2









3
2
4
7









4
2
7
4









5
4
7
2









6
4
2
7









В табл. 2 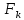, 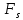– верхняя и нижняя оценки предельной нагрузки, соответственно, V= 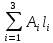– суммарный объем несущих стержней.

2. Основные положения теории предельного равновесия. Ме­тоды решения задач о несущей способности элементов конст­рукций

2.1. Поверхность нагружения

Для математической постановки задачи механики сплошной среды необ­ходимы соотношения, определяющие связь между силовыми и кинематиче­скими параметрами в элементе среды. Разрушение материала (пластическое, или хрупкое) является, как правило, необратимым процессом. Когда дефор­мирование среды является необратимым процессом, поведение материала, предписываемое законом деформирования, должно зависеть от направления процесса. Такая своеобразная неаналитичность приводит к появлению в фа­зовом пространстве внутренних параметров некоторых предельных поверх­ностей, очертание и изменение которых оказывает решающие влияние на форму самого закона деформирования (В. Д. Клюшников [1]).


В результате изменения внешних сил, действующих на тело, и перемеще­ний его границы, происходит изменение напряженно-деформированного со­стояния каждого его элемента. Процесс изменения напряжений в эле­менте называют процессом нагружения, а изменение его деформации – процессом деформирования.

Любой из этих процессов можно представить в виде кривых – траекторий в некоторых фазовых пространствах, координатами которых являются пара­метры либо напряженного, либо деформированного, состояний. В простран­стве напряжений каждому напряженному состоянию отвечает опреде­ленная точка или вектор – вектор напряжений, начало которого совпа­дает с началом координат (ненапряженное состояние), а конец совпадает с данной точкой. Изменению напряженного состояния (догрузке) отвечает вектор , который называют вектором догрузки, процессу изменения на­пряжений – траектория, вычерчиваемая концом вектора (траектория, или путь нагружения).

Аналогичным образом определяют пространство деформаций. Иногда одно и то же девятимерное декартово пространство используют как для представления напряжений, так и для представления деформаций, отклады­вая вдоль данного орта пространства одноиндексные компоненты тензоров (например, и
).

Мы ограничимся рассмотрением только таких материалов, для которых результат деформирования не зависит от скорости процесса нагружения в данное напряженное состояние (упруго-пластические материалы).

Обобщение свойств деформирования упругопластического тела, которые оно проявляет при одноосном растяжении–сжатии, на случай сложного на­пряженного состояния приводит к концепции о существовании поверхности нагружения (В. Д. Клюшников [1]), которая состоит в следующем (рис. 2).



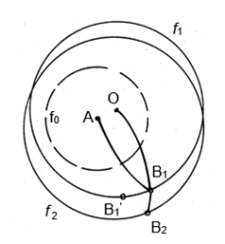
Рис. 2

Для каждой текущей точки произвольной траектории нагружения в пространстве напряжений существует поверхность пределов упругости (поверхность нагружения), все внутренние точки которой достижимы из данной упругим деформированием. Поэтому если, начиная с какой-то точки, траектория нагружения идет внутри поверхности, построенной для этой точки, например , то новых необратимых деформаций не возникает. Считается, что в таком процессе сама поверхность нагружения не изменя­ется; для любой точки такой траектории поверхностью нагружения служит поверхность (начальная поверхность показана на рис. 2 штриховой линией).

Если же траектория выходит наружу поверхности нагружения, построен­ной для предыдущей точки, например, траектория , то возникают новые необратимые деформации. При этом меняется сама поверхность нагружения (ибо она должна содержать текущую точку траектории). Считается, что это изменение поверхности нагружения происходит непрерывно: если отрезок B1B2 мал, то новая поверхность f2, отвечающая точке B2, мало отличается от f1 и в пределе, когда B2→ B1, эти поверхности совпадают.

Смотрите также файлы