, можно найти верхнюю грань , опреде­ляемую неравенством (23). Это значение может совпадать с точным ре­шением, а может являться наилучшим приближением снизу в определенном классе статически допустимых напряжений.

Параметр внешней нагрузки , удовлетворяющий неравенству (24), называют статиче­ски допустимым; значение этого параметра, удовлетво­ряющий неравенству (25), называют кинематически возможным.

Статический и кинематический методы решения задач о несущей способ­ности конструкций основаны на двух теоремах, суть которых изложена в пре­дыдущем разделе. Для сужения "вилки"

(27)

часто используют методы математического, в частности, линейного, программирова­ния.

Общая задача линейного программирования заключается в следующем (Кузнецов Ю.Н., Ку­зубов В.И., Волощенко А.Б. [12]) . Дана линейная целевая функция

(28)

и система линейных ограничений

(29)

, (30)

где n > m; – заданные постоянные величины. Необходимо найти такие неотрицательные значения , кото­рые удовлетворяют системе ограничений (29) и доставляют целевой функ­ции (28) минимальное значение. Об­щая задача линейного программирова­ния имеет несколько форм записи. Наиболее широко ис­пользуемым методом решения общей задачи линейного программирования является так назы­вае­мый симплекс – метод.

Планом, или допустимым решением, задачи линейного программирова­ния называют вектор

---

, удовлетворяющий условиям (29), (30).

Оптимальным планом, или оптимальным решением, задачи линейного программирования на­зывают план, доставляющий наименьшее значение це­левой функции (28).

В статическом методе решения задачи о несущей способности тела ис­пользуют уравнения равновесия (10), (11) и уравнение предельной по­верхности (14). Если в (14) яв­ляется нелинейной функцией, то предельную поверхность аппроксимируют вписанным или опи­санным мно­гогранником. Используя одно из уравнений равновесия, находят выражение для (целевая функция), остальные соотношения образуют систему огра­ничений задачи линейного программирования.

В кинематическом методе используют уравнение баланса мощностей (18), кинематиче­ские граничные условия (12), уравнение предельной по­верхности (14), соотношения ассо­циированного закона деформирования (13) и соотношения (15). Используя (18) определяют выражение для (целевая функция) и некоторое инте­гральное ограничение, остальные ограничения задачи линейного программи­ро­вания следуют из других, используемых в этом методе, соотношений.

Дискретизацию объекта расчета осуществляют, в большинстве случаев, с использованием метода конечных разностей, или метода конечных элемен­тов.

Обзор литературы по теории предельного равновесия приведён, в частности, в работах Сибгатуллина Э. С. [13], [14] и Сибгатуллина К. Э. [15].

3. Пример решения задачи



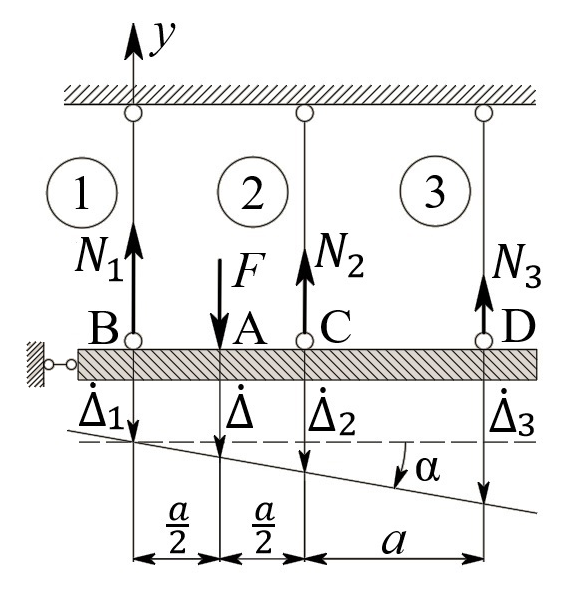
Рис. 4.

Бесконечно жесткий брус подвешен на трех вертикальных стержнях (рис. 4). Известны длины стержней 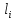, площади поперечных сечений стержней , пределы текучести материалов стержней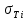

---

(i= 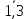). Определить предельную нагрузку 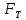для рассматриваемой стержневой системы при 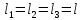, 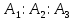= 1:1/2:1/12, .

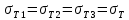3.1. Решение задачи кинематическим методом

Согласно этому методу, истинному механизму разрушения соответствует минимальное значение кинематически возможной нагрузки . Для рассматриваемой системы возможны всего три различных механизма разрушения. Поэтому истинный механизм разрушения с min можно установить путем перебора этих кинематически возможных механизмов разрушения.

Согласно принципу возможных перемещений имеем:

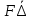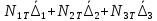= . (31)

Здесь 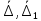, 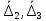– скорости кинематически возможных перемещений точек А, В, С, D, соответственно (рис. 2),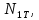 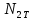, 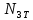– усилия растяжения-сжатия стержней 1, 2, 3, соответственно, в состоянии разрушения системы: , = , .

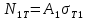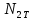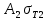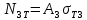Условия совместности скоростей перемещений:

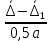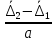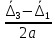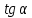= = = . (32)

Так как в кинематическом методе важно только направление вектора скоростей деформации, можно принять следующее дополнительное условие:

---

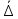=1. (33)

С учетом исходных соотношений между , и условия (33), уравнение (31) можно записать в следующем виде: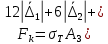

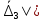| ). (34)

1. Пусть 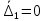; тогда, согласно (32) и (33), имеем 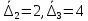. Согласно (34) получаем:

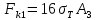. (35)

2. Пусть 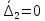; тогда .

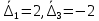Так как скорость диссипации механической энергии не может быть отрицательной величиной, т.е. 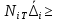0 всегда, в (34) 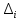необходимо подставлять по модулю. С учетом этого имеем:

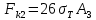. (36)

3. Пусть теперь 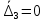; тогда, 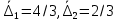. Имеем:

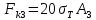. (37)

Из кинематически возможных нагрузок (35, 36, 37) выбираем наименьшее значение:

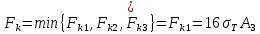. (38)

Значение (38) оценивает действительную разрушающую нагрузку сверху: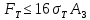

. (39)

---

3.2. Решение задачи статическим методом

В этом случае используем:

а) Уравнения равновесия

∑У=0, ∑ 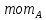=0; (40)

б) Условия прочности

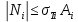(i=1, 2, 3). (41)

Из схемы загружения видно (рис. 4), что в данном конкретном случае 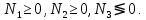С учетом этого (40) и (41) запишем в виде:

, ,

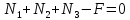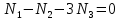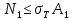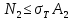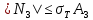, , . (42)

Из второго уравнения (42) находим

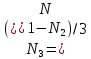. (43)

Подставим (43) в остальные соотношения из (42):

F = (4/3) 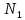+(2/3) 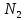, (44)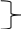

, ,

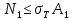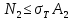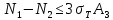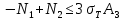, . (45)

Теперь задача формулируется так: найти max F из (44) при выполнении условий (45). Это – задача линейного программирования. В данном случае она может быть решена графически (рис. 5).



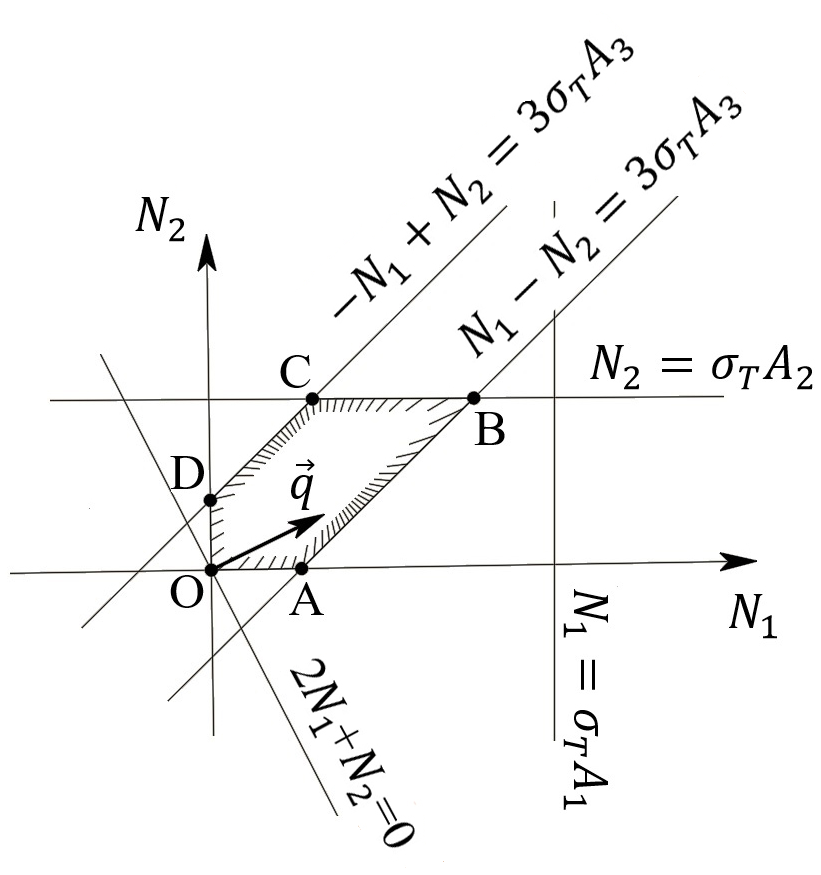
Рис. 5.

Условия (45) в плоскости 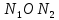выделяют невогнутую область допустимых решений задачи, ограниченную многоугольником OABCDO. Вектор 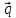, перпендикулярный прямой (4/3) 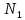+(2/3) 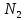=0, показывает направление роста функции (44). Ясно, что в данном случае искомым является решение, соответствующее точке В на рис. 5. Используя координаты точки В, находим:

---

Смотрите также файлы

• Методические рекомендации по суммативному оцениванию Алгебра 8 класс.docx

• 1. Преступление.docx

• Томчак Андрей Николаевич.docx

• Inventors.docx

• Политическая коррупция в системе государственного управления.rtf