Файл: Строение вещества.doc

0. 
   Равновесие реакции 4HCl (г) + O₂ ↔ 2H₂O (г) + 2С1₂ установилось при следующих концентрациях: [Н₂O](г) = [Сl₂] = 0,14, [НCl](г) = 0,2 и [О₂]=0,32 моль/л. Вычислить константу равновесия и начальную концентрацию кислорода.
   

0. 
   Константа равновесия системы 2N₂ + O₂  2N₂O равна 1,21. Равновесные концентрации: N₂ = 0,72 и N₂О = 0,84 моль/л. Найти начальную и равновесную концентрации кислорода.
   
1. 
   Равновесные концентрации веществ в обратимой реакции N₂ + 3H₂  2NH₃ составляют (моль/л): N₂ = 4; Н₂ = 9; NH₃ = 6. Вычислить исходные концентрации азота и водорода и константу равновесия.
   
2. 
   Равновесные концентрации веществ обратимой реакции 2SО₂ + О₂ ↔ 2SО₃ составляют (моль/л): [SО₂]= 0,0002; [О₂]= 0,004; [SО₃]= 0,003. Найти исходные концентрации кислорода и сернистого газа. Вычислить константу равновесия.
   
3. 
   Вычислить начальные концентрации хлора и оксида углерода, а также константу равновесия реакции СО + Сl₂  СОСl₂, если равновесные концентрации (моль/л): С1₂ = 0,3, СО = 0,2; СОСl₂ = 1,5.
   
4. 
   Определить равновесную концентрацию водорода в системе 2HJ  H₂ + J₂, если исходная концентрация HJ составляла 0,05 моль/л, а константа равновесия равна 0,02.
   
5. 
   Константа равновесия реакции N₂ + 3H₂  2NH₃ равна 0,1. Равновесные концентрации Н₂ = 0,2 моль/л и NH₃ = 0,08 моль/л. Вычислить начальную и равновесную концентрации азота.
   
6. 
   Найти равновесные концентрации водорода и йода в системе H₂ + J₂  2HJ, если их начальные концентрации составляли соответственно 0,5 и 1,5 моль/л соответственно, а равновесная концентрация HI равна 0,8 моль/л.
   
7. 
   Константа равновесия реакции СО + H₂O ↔ СO₂ + H₂ при 1090⁰С равна 0,51. Найти состав реакционной смеси в момент достижения равновесия, если в реакцию введено по одному моль оксида углерода (II) и водяного пара.
   
8. 
   Равновесная концентрация HJ в системе H₂ + J₂  2HJ равна 0,04 моль/л, а равновесные концентрации водорода и йода составляют по 0,08 моль/л. Вычислить константу равновесия.
   
9. 
   Исходные концентрации окиси углерода (ІІ) и паров воды равны и составляют по 0,03 моль/л. Вычислить равновесные концентрации СО, H₂O и Н₂ в системе СО + H₂O ↔ СO₂ + H₂, если равновесная концентрация СO₂ оказалась равной 0,01.
   

0. 
   В каком направлении произойдет смещение равновесия при изменении давления в системах:
   

---

а) 2NO + O₂ ↔ 2NO₂; б) 4HCl + O₂ ↔ 2H₂O + 2Cl₂; в) H₂ + S ↔ H₂S?

0. 
   В каком направлении произойдет смещение равновесия при
   повышении температуры систем:
   

а) COCl₂ ↔ СO + Cl₂; ∆H⁰ > 0;

б) 2CO ↔ СO₂ + C; ∆H⁰ < 0;

в) 2SO₃ ↔ 2SO₂ + O₂; ∆H⁰ > 0?

0. 
   В какую сторону сместится равновесие обратимых реакций:
   

а) PCl₅ ↔ PCl₃ + Cl₂; ∆H⁰ =129,6 кДж;

б) N₂ + O₂ ↔ 2NO; ∆H⁰ =179,7 кДж;

в) N₂ + 3H₂ ↔ 2NH₃; ∆H⁰ =-91.9 кДж;

г) CO + H₂O ↔ CO₂ + H₂; ∆H⁰ =-41,8 кДж?

при повышении температуры? При повышении давления?

0. 
   Сместится ли равновесие при сжатии следующих химических систем:
   

а) H₂ + J₂ ↔ 2HJ;

б) 2CO + O₂ ↔ 2СO₂;

в) 2SO₂ + O₂ ↔ 2SO₃ ;

г) CO + H₂O ↔ H₂ + CO₂?

0. 
   Как надо поступить для того, чтобы при данной концентрации исходных веществ максимально повысить выход SO₃ по реакции
   

2SO₂+O₂↔2SO₃; ∆H⁰ = - 188,1 кДж?

0. 
   Рассчитать, как изменятся скорости прямой и обратной реакции при увеличении давления вдвое в системах Н₂ + J₂ ↔ 2HJ и 2NO + O₂ ↔ 2NO₂, в какую сторону сместится равновесие?
   
1. 
   В какую сторону сместится равновесие при повышении температуры в системах:
   

а) N₂ + 3H₂ ↔ 2NH₃; ∆H⁰ = -91,9 кДЖ;

б) N₂O₄ ↔ 2NO₂; ∆H⁰ = -56,8 кДЖ;

в) 2CO + O₂ ↔ 2CO₂ ; ∆H⁰ = 568 кДЖ;

г) N₂ + O₂ ↔ 2NO; ∆H⁰ =-180,7 кДж?

0. 
   Как повлияет на состояние равновесия в системе 4HCl + O₂ ↔ 2H₂O + 2Cl₂ ∆H⁰ < 0 повышение давления и температуры?
   
1. 
   В какую сторону сместится равновесие реакций
   

а) 2H₂S ↔ 2H₂+ S₂; ∆H⁰ = 41,8 кДж;

б) CO + H₂O ↔ CO₂ + H₂ ; ∆H⁰ = 41,8 кДж

а) при понижении температуры; б) при повышении давления?

0. 
   Как отразится повышение давления на равновесии в системах:
   

а) 2H_{2 (г)} + O_{2 (г)} ↔ 2H₂O _(г);

б) CO_{2 (г)} + C_(k) ↔ 2CO _(г);

в) CaCO_{3 (k)} ↔ CaO_(k) + CO_{2 (г)} ?

0. 
   Как повлияет на смещение равновесия реакций
   

а) 2H₂ + O₂ ↔ 2H₂O ; ∆H⁰ > 0;

б) N₂

---

+ O₂ ↔ 2NO; ∆H⁰ < 0

а) повышение температуры; б) уменьшение давления?

0. 
   В какую сторону сместится равновесие при повышении давления в системах:
   

а) PCl₅ ↔ PCl₃ + Cl₂; N₂ + 3H₂ ↔ 2NH₃;

б) 2NO₂ ↔ 2NO + O₂; 2NO₂ ↔ N₂O₄;

в) HJ ↔ H₂ + J₂; N₂ + O₂ ↔ 2NO?

0. 
   В каком направлении сместится равновесие в системе
   

4HCl + O₂  2Cl₂ +2H₂O (∆H⁰ < 0) при

а) повышении температуры;

б) повышении давления (все вещества находятся в газообразном состоянии);

в) как следует изменить температуру и давление, чтобы максимально сместить равновесие вправо?

3. 
   Варианты заданий
   

Номер вари-анта	Номер задачи					Номер вари-анта	Номер задачи
1	2.1	2.31	2.50	2.77	2.93	2.26	2.26	2.37	2.75	2.86	2.99
2	2.2	2.32	2.51	2.78	2.94	2.27	2.27	2.38	2.76	2.87	2.93
3	2.3	2.33	2.52	2.79	2.95	2.28	2.28	2.39	2.50	2.88	2.94
4	2.4	2.34	2.53	2.80	2.96	2.29	2.29	2.40	2.51	2.89	2.95
5	2.5	2.35	2.54	2.81	2.97	2.30	2.30	2.41	2.52	2.90	2.96
6	2.6	2.36	2.55	2.82	2.98	2.31	2.1	2.42	2.53	2.91	2.97
7	2.7	2.37	2.56	2.83	2.99	2.32	2.2	2.43	2.54	2.92	2.98
8	2.8	2.38	2.57	2.84	2.100	2.33	2.3	2.44	2.55	2.77	2.99
9	2.9	2.39	2.58	2.85	2.101	2.34	2.4	2.45	2.56	2.78	2.100
10	2.10	2.40	2.59	2.86	2.102	2.35	2.5	2.46	2.57	2.79	2.101
11	2.11	2.41	2.60	2.87	2.101	2.36	2.6	2.47	2.58	2.80	2.102
12	2.12	2.42	2.61	2.88	2.100	2.37	2.7	2.48	2.59	2.81	2.101
13	2.13	2.43	2.62	2.89	2.105	2.38	2.8	2.49	2.60	2.82	2.100
14	2.14	2.44	2.63	2.90	2.93	2.39	2.9	2.31	2.61	2.83	2.105
15	2.15	2.45	2.64	2.91	2.94	2.40	2.10	2.32	2.62	2.84	2.93
16	2.16	2.46	2.65	2.92	2.95	2.41	2.11	2.33	2.63	2.85	2.94
17	2.17	2.47	2.66	2.77	2.96	2.42	2.12	2.34	2.64	2.86	2.95
18	2.18	2.48	2.67	2.78	2.97	2.43	2.13	2.35	2.65	2.87	2.96
19	2.19	2.49	2.68	2.79	2.98	2.44	2.14	2.36	2.66	2.88	2.97
20	2.20	2.31	2.69	2.80	2.99	2.45	2.15	2.37	2.67	2.89	2.98

---

Продолжение

21	2.21	2.32	2.70	2.81	2.100	2.46	2.16	2.38	2.68	2.90	2.99
22	2.22	2.33	2.71	2.82	2.101	2.47	2.17	2.39	2.69	2.91	2.100
23	2.23	2.34	2.72	2.83	2.102	2.48	2.18	2.40	2.70	2.92	2.101
24	2.24	2.35	2.73	2.84	2.101	2.49	2.19	2.41	2.71	2.77	2.102
25	25	2.36	2.74	2.85	2.100	2.50	2.20	2.42	2.72	2.78	2.101

---

Список рекомендуемой литературы
1. Глинка Н.Л., Ермаков А.И. Общая химия: учеб. пособие для вузов

/под ред. А.И. Ермакова.-29-е изд., испр.-М.: Интеграл-Пресс, 2004.-728 с.

2. Глинка Н.Л.Задачи и упражнения по общей химии.-М.:Интеграл-пресс, 2006.- 240с.

3. Коровин М.В. Общая химия. - М.: Высшая школа, 2006. - 557 с.

Задание № 4 по теме «Растворы»

1. 
   Примеры решения задач
   

1.1. ПРОЦЕНТНАЯ КОНЦЕНТРАЦИЯ

Пример 1

а) Определите массовую долю (%) хлорида калия в растворе, содержащем 0,053 кг KCl в 0,5 л раствора, плотность которого 1063 кг/м³.

Решение:

Массовая доля ω или С% показывает, сколько единиц массы растворенного вещества содержится в 100 единицах массы раствора. Массовая доля - безразмерная величина, ее выражают в долях единицы или процентах:



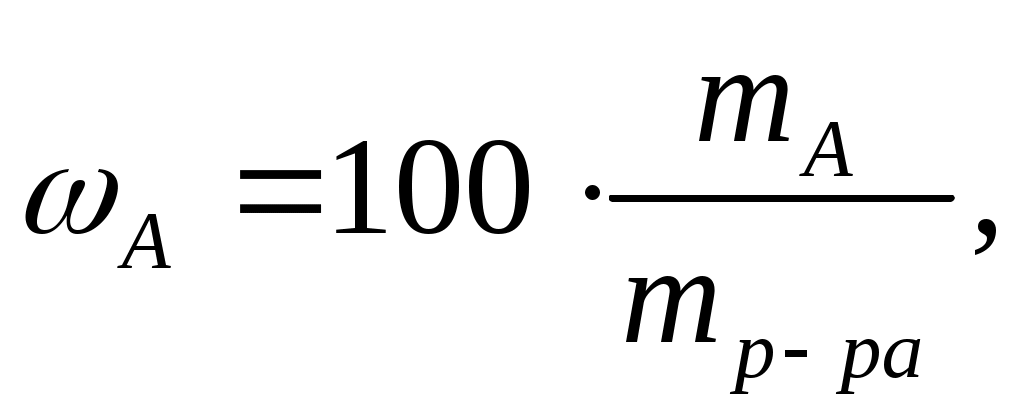
где ω_A - массовая доля (%) растворенного вещества;

m_A- масса растворенного вещества, г;

m_р-ра – масса раствора, г.

Масса раствора равна произведению объема раствора V на его плотность ρ:

m=ρV, тогда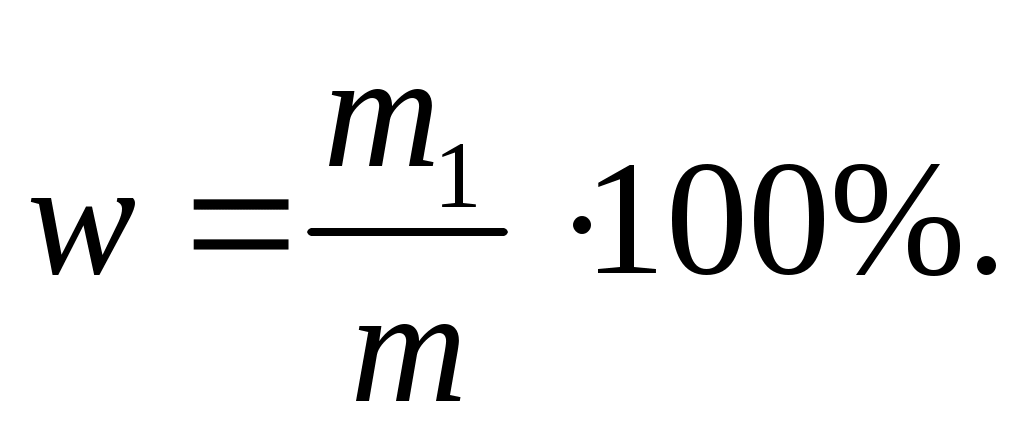

Массовая доля хлорида калия в растворе равна:


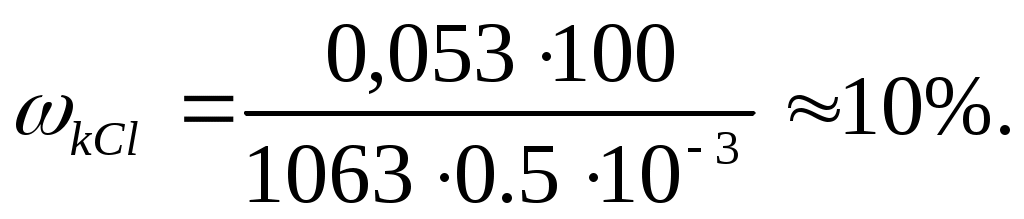
Пример 2

Какой объем раствора азотной кислоты с массовой долей HNO₃ 30% (ρ=1180кг/м³) требуется для приготовления 20 л 0,5 М раствора этой кислоты?

Решение: Сначала определяем массу азотной кислоты в 20 л 0,5 М раствора:



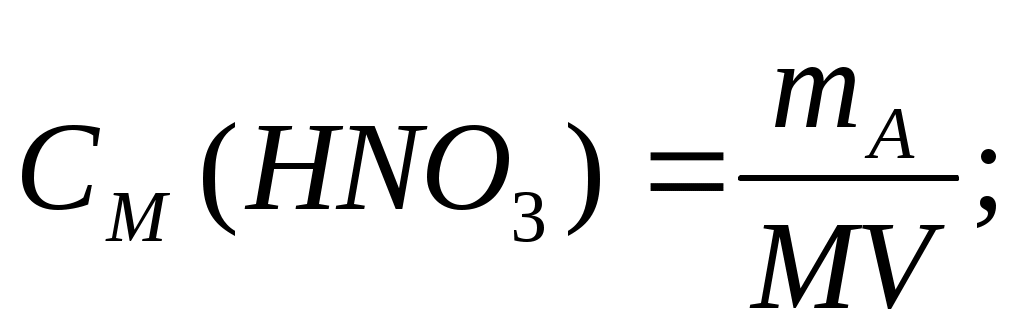
M (HNO₃)=63,01 г/моль;

m_HNO3=0,5∙63,01∙20=630,1 г.

Определим, в каком объеме раствора с массовой долей HNO₃ 30% содержится 630,1 г HNO₃ :



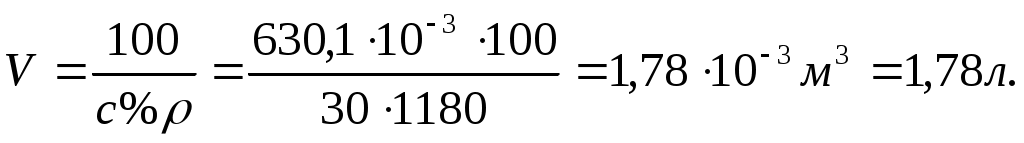
Следовательно , чтобы приготовить 20 л 0,5 М HNO₃, надо израсходовать всего 1,78 л раствора азотной кислоты с массовой долей HNO₃ равной 30%.
Пример 3

Какую массу раствора с массовой долей КОН 20% надо прибавить к 250 г раствора с массовой долей КОН 90%, чтобы получить раствор с ω_КОН=50 %?

Решение: Задача решается с помощью правила смешения. Массу раствора с массовой долей КОН 20 % обозначим через х.

Тогда 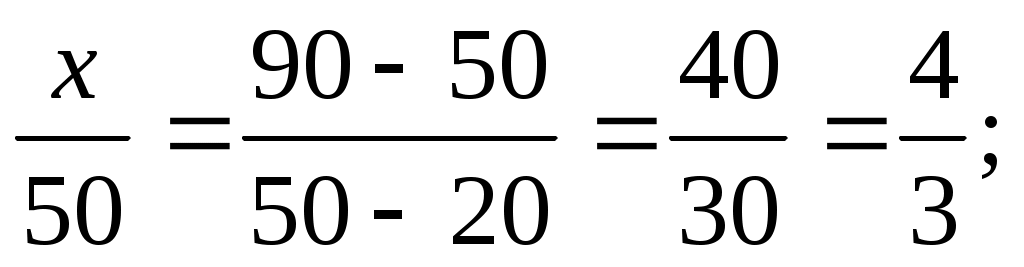3х=1000; х=333,3.

Для получения раствора с массовой долей КОН 50 % необходимо к 250 г раствора КОН с ω=90 % прибавить 333,3 г раствора КОН с 20 %.

Задачи такого типа решают с помощью диагональной схемы или «правила креста»: точкой пересечения двух отрезков прямой обозначают свойства смеси, которую необходимо получить.
20 (90-50)=40



50

90 (50-20)=30

Массы исходных растворов, необходимые для приготовления смеси, обратно пропорциональны разностям между концентрациями заданного и менее концентрированного раствора и более концентрированного и заданного растворов:



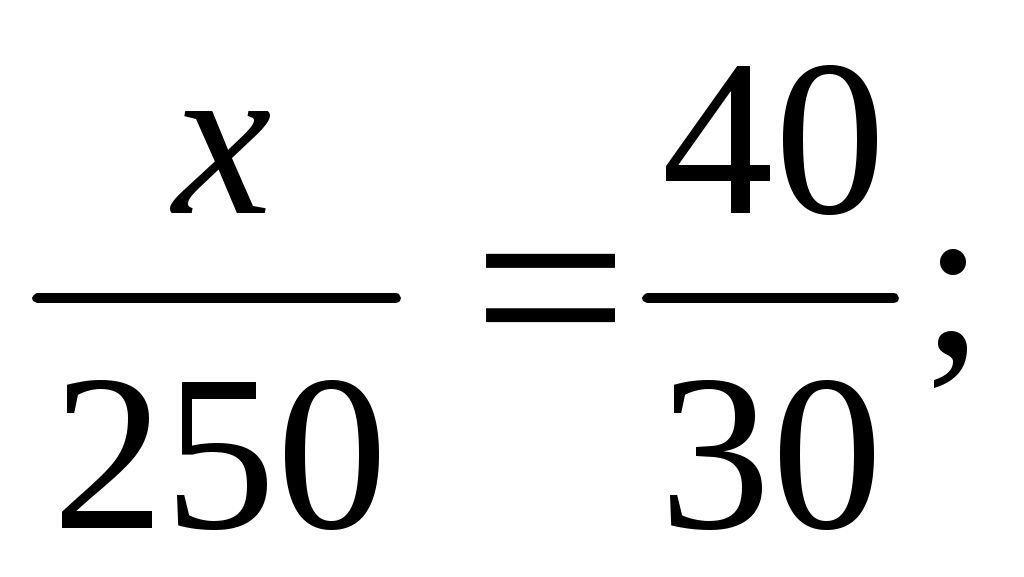
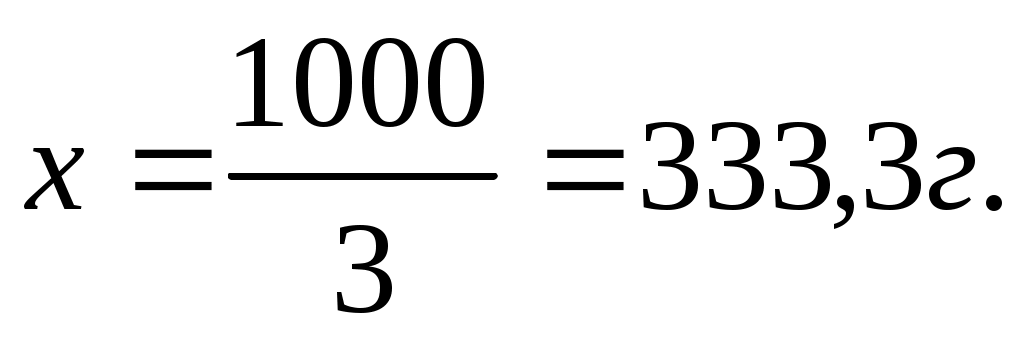
Также эту задачу можно решить, учитывая, что при сливании двух растворов суммируется масса растворенного вещества. Пусть масса 20% раствора х г, тогда масса КОН в нем 0,2 х. Масса КОН во втором растворе 0,9 · 250 = 225 г. Масса вещества в итоговом растворе 0,5 · (250 + х). Таким образом,

0,2х + 225 = 0,5(250+х); х=333,3 г.

2. 
   МОЛЯРНАЯ И ЭКВИВАЛЕНТНАЯ КОНЦЕНТРАЦИИ
   

Пример 1

Какова масса NaOH, содержащегося в 0,2 л раствора, если молярная концентрация раствора 0,2 моль/л?

Решение:

Молярная концентрация С_м или М (молярность) показывает количество растворенного вещества, содержащегося в 1 л раствора.

Молярную концентрацию (моль/л) выражают формулой



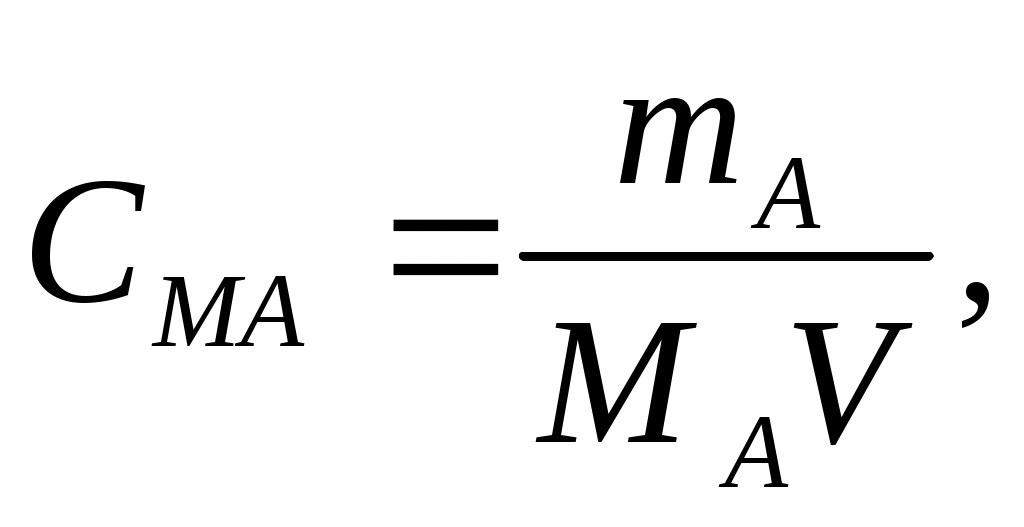
где m₁ - масса растворенного вещества, г;

M - молярная масса растворенного вещества, г/моль;

V - объем раствора, л.
M (NaOН)=40 г/моль. Масса NaOH, содержащегося в растворе, равна

M_NaOH=MV=0,2∙40∙0,2=1,6 г.
Пример 2

Определите молярную концентрацию эквивалента хлорида железа (ІІІ), если в 0,3 л раствора содержится 32,44 г FeCl₃.

Решение:

Молярная концентрация эквивалента вещества (нормальность) показывает число молярных масс эквивалентов растворенного вещества, содержащихся в 1л раствора (моль/л):


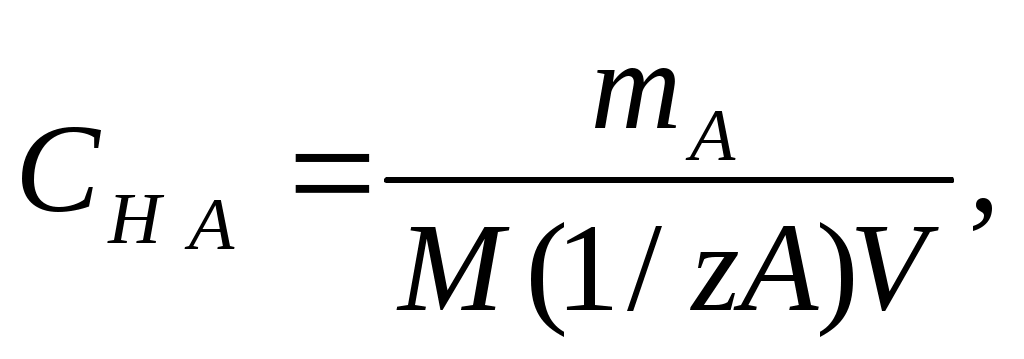
где m_А - масса растворенного вещества, г;

M (1/zА) - молярная масса эквивалента растворенного вещества, г/моль;

V – объем раствора, л.

Молярная масса эквивалента FeCl₃ равна


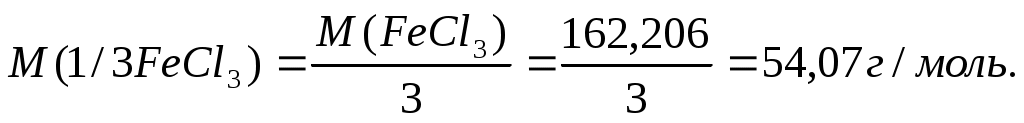
Молярная концентрация эквивалента раствора FeCl₃ равна


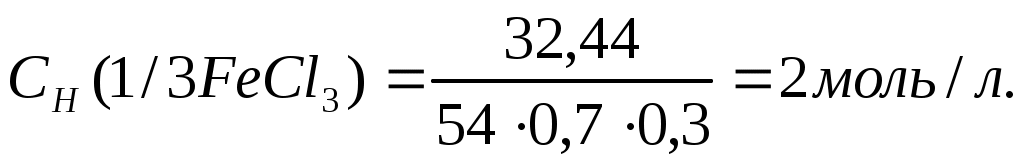
Пример 3

Определите концентрацию раствора КОН, если на нейтрализацию 0,035 л 0,3 н. H₃PO₄ израсходовано 0,02 л раствора КОН.

Решение:

Из закона эквивалентов следует, что количество эквивалентов веществ участвующих в химической реакции одинаково. В реакции участвуют 0,035·0,3=0,0105 эквивалента фосфорной кислоты. Для нейтрализации H₃PO₄

потребуется такое же количество вещества эквивалента КОН, т.е.

V(H₃PO₄)С_Н(H₃PO₄)=V(KOH)С_Н(KOH).

Отсюда



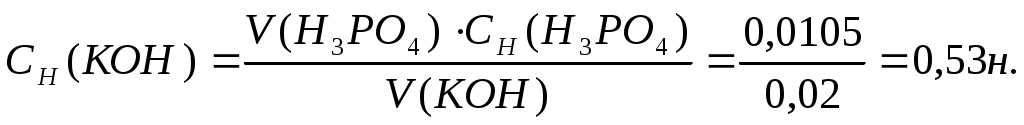
1.3. МОЛЯЛЬНАЯ КОНЦЕНТРАЦИЯ (МОЛЯЛЬНОСТЬ) , МОЛЬНАЯ ДОЛЯ, ТИТР
Пример 1

В какой массе эфира надо растворить 3,04 г анилина C₆H₅NH₂ , чтобы получить раствор, моляльность которого равна 0,3 моль/кг?

Решение:

Моляльность раствора Сm (моль/кг) показывает количество растворенного вещества, находящегося в 1 кг растворителя:



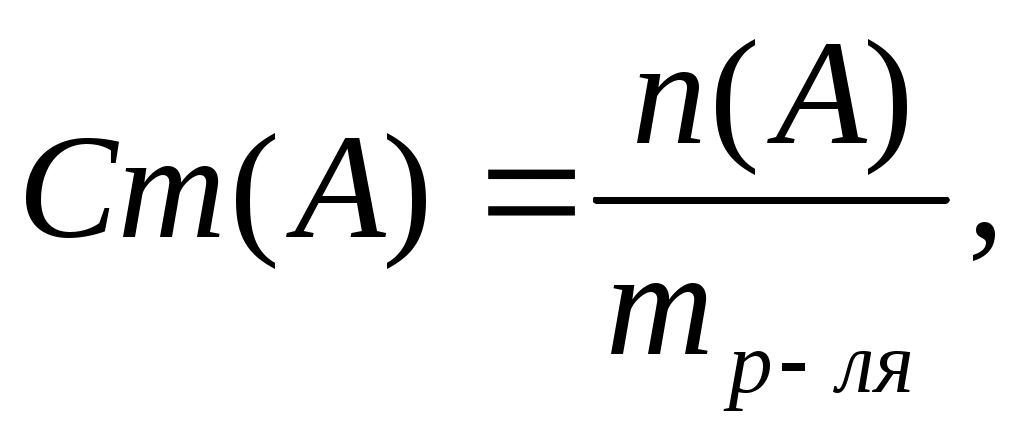
где m_р-ля – масса растворителя, кг;

n (А) – количество растворенного вещества, моль.

M (C₆H₅NH₂ ) - 99,13 г/моль.

Масса растворителя (эфира) равна:

т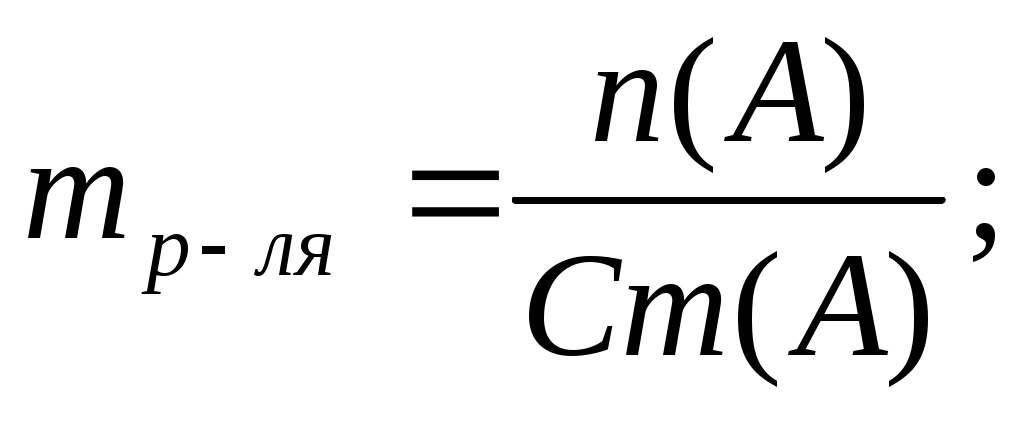 огда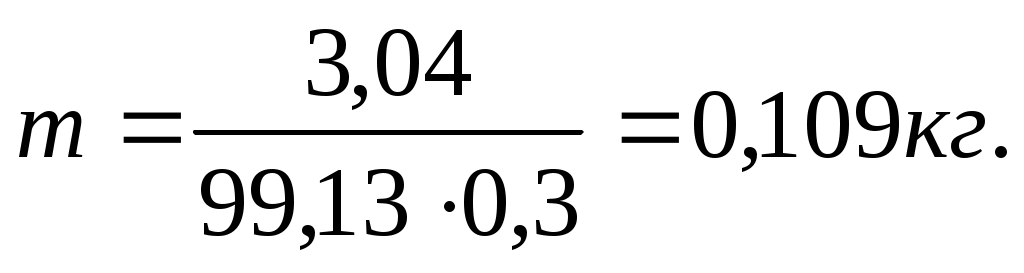
Пример 2

Определите титр 0,01 н. КОН.

Решение:

Титр раствора показывает массу (г) растворенного вещества, содержащегося в 1 мл раствора. В 1 л 0,01 н. КОН содержится 0,564 г КОН. Титр этого раствора равен:

Т= 0,561/1000=0,000561 г/мл.
Пример 3

Рассчитайте молярные доли глюкозы C₆H₁₂O₆ и воды в растворе с массовой долей глюкозы 36 %.

Решение:

Мольная доля вещества А(χ_А) в растворе равна отношению количества данного вещества n_А к общему количеству всех веществ, содержащихся в растворе:



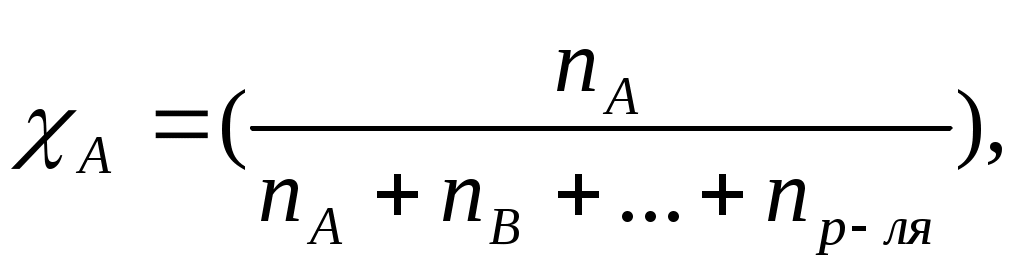
где (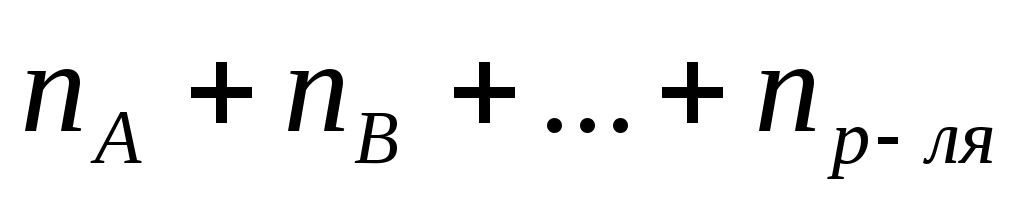 ) количество всех веществ, содержащихся в растворе.

В 100 г раствора с массовой долей глюкозы, равной 36 %, содержится 36 г глюкозы и 64 г воды:

nC₆H₁₂O₆ =36/180=0,20 моль;

nH₂O= 64/18= 3,56 моль;

nC₆H₁₂O₆ + nH₂O= 0,20 + 3,56 =3,76 моль;

χC₆H₁₂O₆= 0,20/3,76= 0,053;

χH₂O= 3,56/3,76= 0,947.

Сумма молярных долей всех компонентов раствора равна 1.
Пример 4

Вычислите молярную концентрацию эквивалента, молярную концентрацию и моляльность раствора, в котором массовая доля CuSO₄ равна 10 %. Плотность раствора 1107 кг/м³.

Решение:

Определим молярную массу и молярную массу эквивалента CuSO₄:

M (CuSO₄)= 159,61 г/моль; M(1/2 CuSO₄)=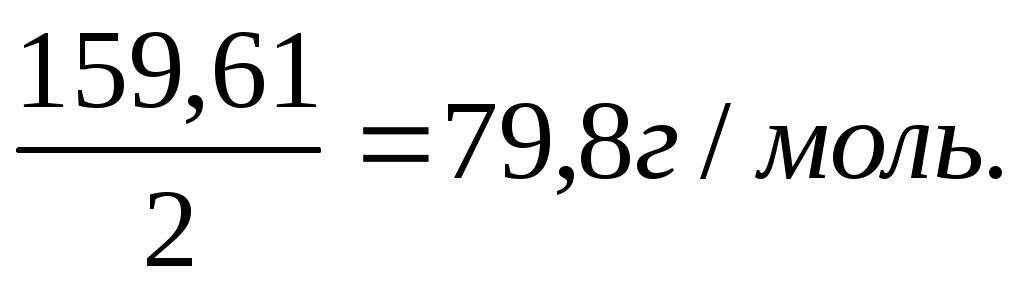

В 100 г раствора с ωCuSO₄=10 % содержится 10,0 г CuSO₄ и 90 г H₂O.

Следовательно, моляльность раствора CuSO₄ равна

Сm(CuSO₄/H₂O)=10/(159,61∙0,09)=0,696 моль/кг.

Молярная концентрация и молярная концентрация эквивалента относятся к 1л раствора:

m_р-ра= ρV= 1107·10^-3=1,107 кг.

В этой массе раствора содержится 1,107·0,1=0,1107 кг CuSO_4, что составляет 110,7/159,61=0,693 моль, или 0,693·2=1,386 экв.

Молярная концентрация и молярная концентрация эквивалента данного раствора соответственно равны 0,693 и 1,386 моль/л.
1.4. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ. ЗАКОН ВАНТ- ГОФФА
Пример 1

Вычисление осмотического давления растворов.

Вычислите осмотическое давление раствора, содержащего в

1,4 л 63 г глюкозы С₆Н₁₂О₆ при 0°С.

Решение:

Осмотическое давление раствора определяют согласно закону Вант-Гоффа:

Pocм = nRT/V,

где п — количество растворенного вещества, моль;

V – объем раствора, м³;

R— молярная газовая постоянная, равная 8,3144 Дж/(моль-К).

В 1,4 л раствора содержится 63 г глюкозы, молярная масса которой равна 180,16 г/моль. Следовательно, в 1,4л раствора содержится

n= 63/180,16=0,35моль глюкозы.

Осмотическое давление этого раствора глюкозы:



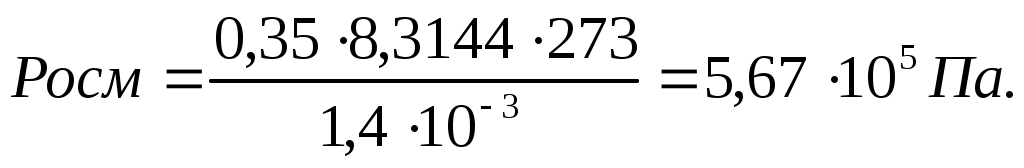
Пример 2

Определение молекулярной массы неэлектролита по осмотическому давлению раствора.

Рассчитайте молекулярную массу неэлектролита, если в 5л раствора содержится 2,5 г неэлектролита. Осмотическое давление этого раствора равно 0,23∙10⁵ Па при 20°С.

Решение:

Заменив п выражением m/M, где т — масса растворенного вещества, а М — его молярная масса, получим

Росм = mRT/(MV).

Отсюда молярная масса растворенного вещества равна



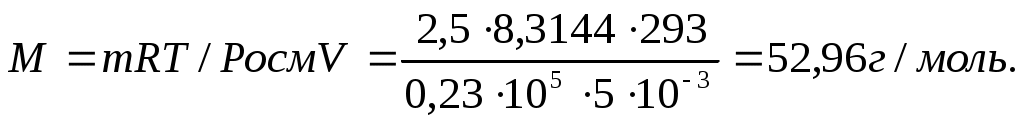
Следовательно, молекулярная масса неэлектролита равна 52,96

Росм кПа: R=8,31 Дж/моль∙К;

Росм мм Hg ст.: R=62,32 л∙мм.рт.ст./град.∙моль;

Росм. атм.: R=0,082 л∙атм../град.∙моль.

1.5. ДАВЛЕНИЕ НАСЫЩЕННОГО ПАРА РАСТВОРОВ. ТОНОМЕТРИЧЕСКИЙ ЗАКОН РАУЛЯ
Пример 1

а) Вычислите давление пара над раствором, содержащим 34,23 г сахара C₁₂H₂₂O₁₁ в 45,05 г воды при 65 ºС, если давление паров воды при этой температуре равно 2,5·10⁴ Па.

Решение:

Давление пара над раствором нелетучего вещества в растворителе всегда ниже давления пара над чистым растворителем при той же температуре. Относительное понижение давления пара растворителя над раствором согласно закону Рауля выражается соотношением



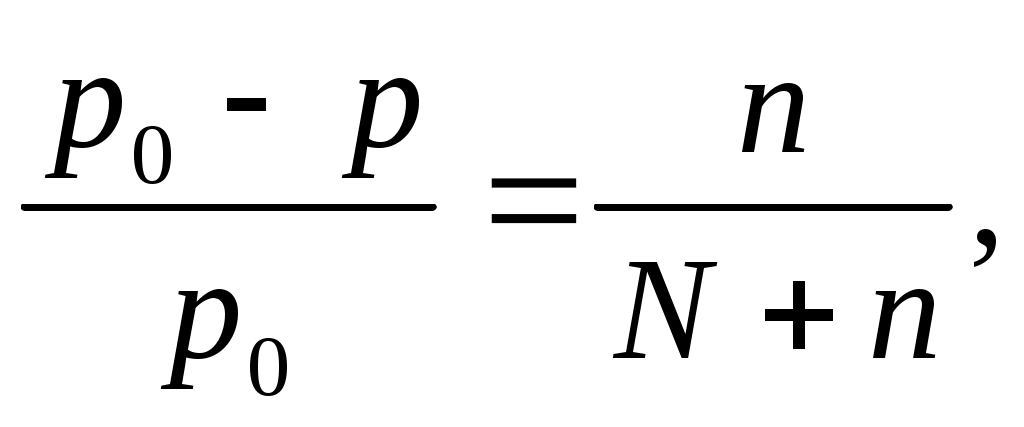
где p₀ – давление пара над чистым растворителем;

p – давление пара растворителя над раствором;

n – количество растворенного вещества, моль;

N – количество растворителя, моль;

M (C₁₂H₂₂O₁₁) = 342,30 г/моль;

M (H₂O) = 18,02 г/моль.

Количество растворенного вещества и растворителя: n=34,23/342,30=0,1 моль; N = 45,05/18,02= 2,5моль.

Давление пара над раствором:



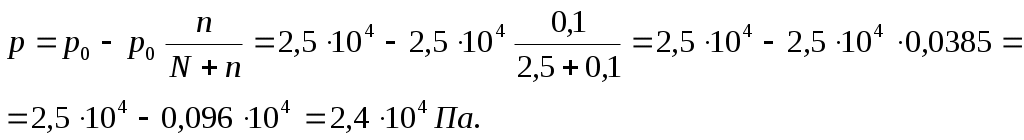
Пример 2

Рассчитайте молекулярную массу неэлектролита, если 28,5 г этого вещества, растворенного в 785 г воды, вызывают понижение давления пара воды над раствором на 52,37 Па при 40°С. Давление водяного пара при этой температуре равно 7375,9 Па.

Решение:

Относительное понижение давления пара растворителя над раствором равно



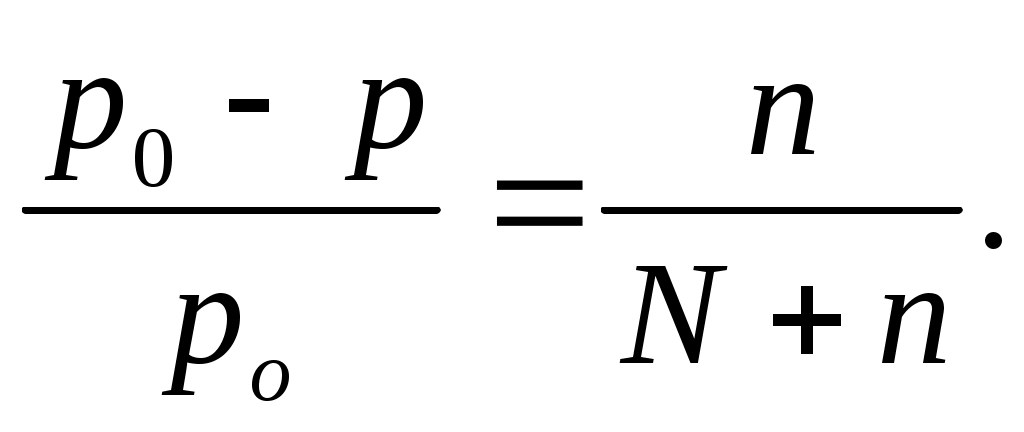
Находим: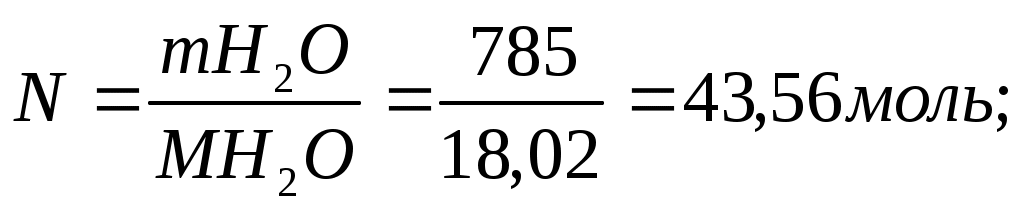

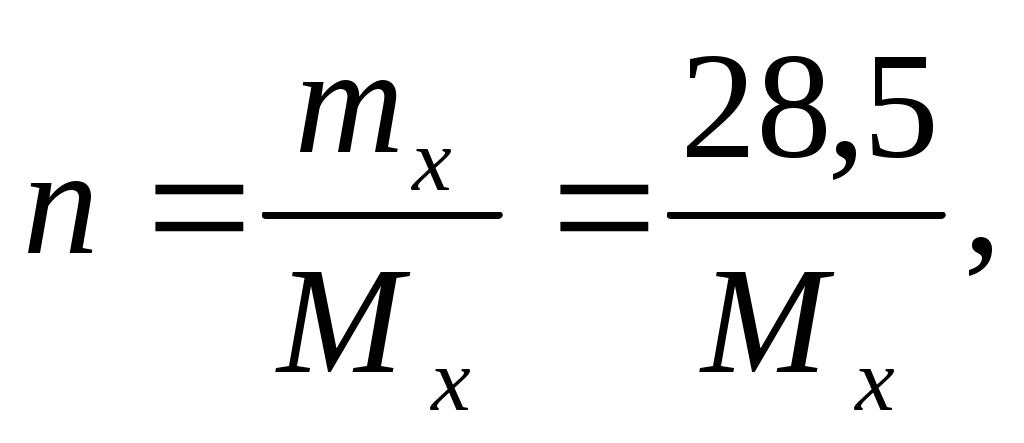здесь m_x – масса неэлектролита, молярная масса которого

M_x г/моль.

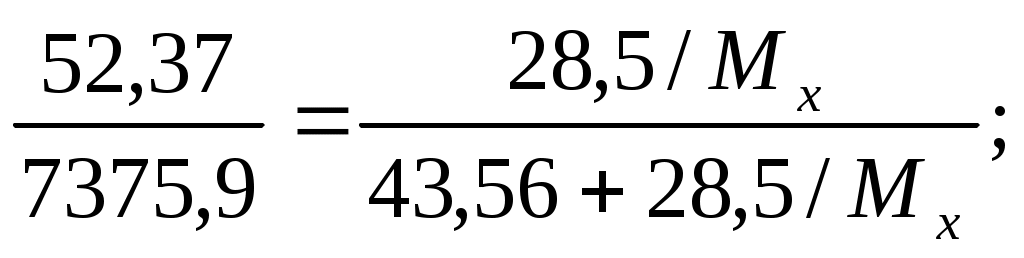0,309M_x + 0,202=28,5;

0,309M_x =28,298;

M_x=91,58 г/моль.

Молекулярная масса неэлектролита равна

92.

---