ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 194
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В методических указаниях представлены краткий материал по описанию метода анализа иерархий, примеры решения экономических задач, задания для самостоятельного выполнения и контрольные задания по тематике лабораторного практикума. Для магистрантов 2 курса, обучающихся по направлению 03.04.01 «Экономика» магистерской программы «Учет, анализ и аудит» (заочная форма обучения).
Введение
При системном исследовании (анализе) сложных социально-экономических систем в их развитии, как известно [6], базовая методика системного анализа включает в себя10 основных этапов:
-
формулировка проблемы;
-
формулировка проблематики;
-
конфигурирование проблемы;
-
постановка задачи;
-
определение глобальной цели и построение дерева целей;
-
выбор критериев для сравнения альтернативных путей достижения цели (далее кратко «альтернатив»);
-
генерирование альтернатив;
-
моделирование;
-
синтез решения;
-
реализация решения.
При этом предпоследний 9-й этап неизбежно связан с многокритериальным выбором оптимальной альтернативы среди нескольких, прогенерированных на седьмом этапе.
При принятии управленческих решений и прогнозировании возможных результатов лицо, принимающее решение (ЛПР), обычно сталкивается со сложной системой взаимозависимых компонент (ресурсы, желаемые исходы, цели, лица и группы лиц и т.д.), которую нужно проанализировать. Чем лучше ЛПР вникает в эту сложность, тем лучше будут его прогнозы и принимаемые решения. И в этом процессе исследования сложной системы большое значение имеет модель поддержки принятия решения ЛПР.
Если удалось связать критерии с альтернативами и ограничениями в соответствующей количественной модели исследуемой системы, то можно применить один из методов многокритериальной оптимизации [2, 8]. Однако для сложных нелинейных многомерных систем часто не удается их формализовать и описать комплексом количественных моделей. В таких случаях при решении задач многокритериального выбора прибегают к методам экспертных оценок при разработке критериев и определении наилучшей альтернативы.
Здесь возникает принципиальное затруднение, связанное с субъективным характером экспертных оценок: они сильно зависят от квалификации каждого члена группы экспертов, суждения разных экспертов могут быть плохо согласованными и алгоритм выбора оптимальной альтернативы плохо формализуем.
Рассматриваемый ниже метод анализа иерархий (МАИ), разработанный американским ученым Томасов Саати в 1968 году, во многом лишен указанных выше недостатков. В МАИ процесс разработки управленческих решений в основном формализован: экспертные оценки используются только на стадии постановки задачи при формировании так называемой «матрицы суждений». Применение метода сводит исследование даже очень сложных систем к последовательности попарных сравнений соответствующим образом определенных компонент.
Отметим основные преимущества МАИ:
-
Теория МАИ отражает естественный ход человеческого мышления. При анализе сложной системы для выработки управленческих решений человеческий разум объединяет их в группы в соответствии с распределением некоторых свойств между элементами. Общие свойства этих групп рассматриваются в качестве элементов следующего (снизу-вверх) уровня иерархии. Эти элементы вышестоящего уровня, в свою очередь, могут быть сгруппированы в соответствии с другим набором свойств, создавая элементы еще одного, более высокого уровня. Итак, до тех пор, пока не будет достигнут единственный элемент – вершина иерархии, который отождествляется с целью процесса принятия решения.
-
В МАИ сочетаются методы количественных и экспертных оценок на основе построения иерархических отношений между альтернативными объектами и критериями, а также использование рассуждений в терминах шкалы отношений. Этот метод позволяет изучать и анализировать отношения между альтернативными объектами на основе интерпретации целей отбора. В данном методе опыт и интуиция играют не менее важную роль, чем расчеты количественных показателей. Может оказаться так, что некоторый фактор с невысокой степенью влияния на величину критерия, будет обладать существенным системным влиянием из-за косвенных взаимодействий с другими важными факторами. Именно многокритериальная логика является тем методом, который позволяет рассмотреть проблему целиком и является полезным и незаменимым инструментом отбора альтернатив по множеству критериев.
-
МАИ сочетает в себе простоту и прозрачную логику алгоритма с общностью в аспекте возможности применения для самых разных систем.
-
Метод хорошо обоснован математически его автором Т. Саати в [1], а также опытом его применения автором и его последователями. Так в [1] приводится пример решения ряда серьезных задач: анализ влияния состояния «ни мир, ни война» на экономической, политической и военный статус Египта летом 1972г.; исследование транспортной системы Судана в 1973г.; анализ терроризма для агентства по контролю над вооружениями в Вашингтоне (США); решение вопроса о размещении ресурсов в соответствии с приоритетами для крупных частных, правительственных и международных концернов и др.
В настоящее время МАИ нашел свое широкое применение в задачах многокритериального принятия решений, стратегического планирования и распределения ресурсов, задачах разрешения конфликтов и других проблемах системных исследований сложных социально-экономических систем, в учебных и научных учреждениях, властных структурах и промышленных корпорациях.
Целью лабораторной работы является развитие у студентов навыков постановки и решения многокритериальных задач выбора, возникающих при решении сложных проблем в социально-экономических системах.
1. Краткие теоретические сведения о собственных векторах и собственных значениях матрицы
Прежде, чем изложить подробно алгоритм МАИ и описать пример его применения, приведем элементарные сведения о понятиях «собственный вектор» (СВ) матрицы и ее «собственное значение» (СЗ), поскольку МАИ основан на использовании этих понятий и математическим аппарате линейной алгебры.
Определение. Число λ называется собственным значением (или характеристическим числом) квадратной матрицы А порядка n, если можно подобрать такой n-мерный ненулевой вектор 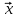 , что выполняется уравнение [10, с. 70]:
, что выполняется уравнение [10, с. 70]:
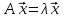 или
или 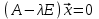 . (1)
. (1)
Множество всех собственных значений 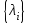 матрицы А находится как корни характеристического или «векового» уравнения
матрицы А находится как корни характеристического или «векового» уравнения
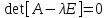 , (2)
, (2)
где λ – рассматривается в качестве независимых переменных; Е – матричная единица; det(·) – определитель матрицы.
Замечание 1. Если выполнить операцию вычисления определителя det(·) в (2), то получим выражение для характеристического полинома относительно собственных чисел:
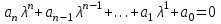 . (3)
. (3)
Решение систем линейных однородных уравнений вида (1) и (2) основано на известной лемме из теории матриц [9, с. 54]: «Для того, чтобы линейная система однородных алгебраических уравнений имела нетривиальное решение, необходимо и достаточно равенство нулю ее определителя».
Пример. Найти собственные значения и собственные векторы матрицы
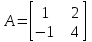 .
.
-
Запишем характеристическое уравнение матрицы
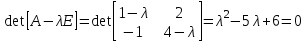 .
.
То есть получилось квадратное уравнение (характеристический многочлен) относительно неизвестных значений λ.
-
Решением этого квадратного уравнения будут корни:
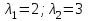 .
.
-
Найдем собственные векторы, принадлежащие собственным значениям. Собственный вектор, принадлежащий собственному значению 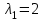 , по определению является ненулевым решением системы
, по определению является ненулевым решением системы
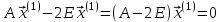 . (4)
. (4)
Верхний индекс в скобках означает принадлежность к собственному значению 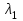 , а нижний индекс – это номер простого (не кратного) корня.
, а нижний индекс – это номер простого (не кратного) корня.
Поучим:
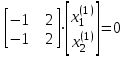 .
.
-
Проверяем условие цитированной выше леммы:
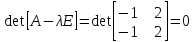 .
.
Условия выполнены, значит нетривиальное решение (3) существует. Тогда в простейшем случае системы двух уравнений [9, с. 336]:
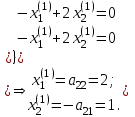
Таким образом, ненулевой собственный вектор, принадлежащий собственному числу 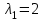 , найден:
, найден:
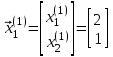 .
.
Аналогично находится второй собственный вектор 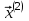 матрицы А, принадлежащий собственному значению
матрицы А, принадлежащий собственному значению 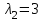 .
.
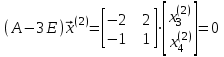 ;
; 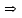
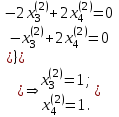
Следовательно, второй собственный вектор, принадлежащий собственному числу 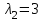 , равен
, равен
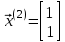 .
.
Замечание. Метод нахождения собственных чисел 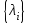 и собственных векторов из [9, с. 336] неэффективен с точки зрения вычислительной математики при высоком порядке матрицы А (n
и собственных векторов из [9, с. 336] неэффективен с точки зрения вычислительной математики при высоком порядке матрицы А (n
сотни и тысячи).
формулировка проблемы;
формулировка проблематики;
конфигурирование проблемы;
постановка задачи;
определение глобальной цели и построение дерева целей;
выбор критериев для сравнения альтернативных путей достижения цели (далее кратко «альтернатив»);
генерирование альтернатив;
моделирование;
синтез решения;
реализация решения.
Теория МАИ отражает естественный ход человеческого мышления. При анализе сложной системы для выработки управленческих решений человеческий разум объединяет их в группы в соответствии с распределением некоторых свойств между элементами. Общие свойства этих групп рассматриваются в качестве элементов следующего (снизу-вверх) уровня иерархии. Эти элементы вышестоящего уровня, в свою очередь, могут быть сгруппированы в соответствии с другим набором свойств, создавая элементы еще одного, более высокого уровня. Итак, до тех пор, пока не будет достигнут единственный элемент – вершина иерархии, который отождествляется с целью процесса принятия решения.
В МАИ сочетаются методы количественных и экспертных оценок на основе построения иерархических отношений между альтернативными объектами и критериями, а также использование рассуждений в терминах шкалы отношений. Этот метод позволяет изучать и анализировать отношения между альтернативными объектами на основе интерпретации целей отбора. В данном методе опыт и интуиция играют не менее важную роль, чем расчеты количественных показателей. Может оказаться так, что некоторый фактор с невысокой степенью влияния на величину критерия, будет обладать существенным системным влиянием из-за косвенных взаимодействий с другими важными факторами. Именно многокритериальная логика является тем методом, который позволяет рассмотреть проблему целиком и является полезным и незаменимым инструментом отбора альтернатив по множеству критериев.
МАИ сочетает в себе простоту и прозрачную логику алгоритма с общностью в аспекте возможности применения для самых разных систем.
Метод хорошо обоснован математически его автором Т. Саати в [1], а также опытом его применения автором и его последователями. Так в [1] приводится пример решения ряда серьезных задач: анализ влияния состояния «ни мир, ни война» на экономической, политической и военный статус Египта летом 1972г.; исследование транспортной системы Судана в 1973г.; анализ терроризма для агентства по контролю над вооружениями в Вашингтоне (США); решение вопроса о размещении ресурсов в соответствии с приоритетами для крупных частных, правительственных и международных концернов и др.
Запишем характеристическое уравнение матрицы
Решением этого квадратного уравнения будут корни:
Найдем собственные векторы, принадлежащие собственным значениям. Собственный вектор, принадлежащий собственному значению
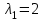 , по определению является ненулевым решением системы
, по определению является ненулевым решением системыПроверяем условие цитированной выше леммы:
В вычислительной математике известны различные вычислительные схемы определения собственных чисел и собственных векторов матрицы, и имеются соответствующие пакеты программ для ЭВМ. Однако до настоящего времени общепринятый стандартный простой метод решения проблемы на собственные значения и собственные векторы матриц большого размера отсутствует.
Если под рукой нет подходящей программы, то можно применить один из простых приближенных методов, описанных в [1, с. 32]. В лабораторной работе применен метод под номером 4, использующий среднегеометрическую оценку компонент собственного вектора (см. ниже таблицу 6).
2. Алгоритм метода анализа иерархий
Изложение алгоритма МАИ приведем, следуя [1] и [5], для наглядности совместив формальное описание с примером.
2.1. Основные положения
Метод анализа иерархий является систематической процедурой для иерархического представления компонентов, определяющих суть любой проблемы. Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решение (ЛПР), по парным сравнениям. В результате может быть выражена относительная степень взаимодействия элементов. Эти суждения затем выражаются численно. Метод анализа иерархии включает процедуры синтеза множественных суждений, выявления приоритетности критериев и нахождения альтернативных решений. Полученные таким образом значения являются оценками в шкале отношений и соответствуют некоторым численным оценкам.
Решение проблемы – это процедура поэтапного установления приоритетов. На первом этапе выявляются наиболее важные компоненты проблемы, на втором – наилучший способ проверки наблюдений, испытания и оценка альтернатив; на следующем этапе вырабатывается решение и оценивается его качество. Процесс может быть проведен также над последовательностью иерархий: в этом случае результаты, полученные в одной из них, используются в качестве входных данных при изучении следующей. Метод многокритериального отбора систематизирует процесс решения такой многоступенчатой задачи.
Основные принципы метода анализа иерархий
1. Принцип идентичности и декомпозиции
. Предусматривает структурирование проблем в виде иерархии или сети.
2. Принцип сравнительный суждений (парных сравнений). Предполагает, что элементы задачи (альтернативы и критерии) сравниваются попарно с позиции их воздействия на общую характеристику.
3. Принцип синтеза приоритетов. Предполагает формирование набора локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня.
2.2. Постановка задачи (пример)
Целью задачи является строительство аэропорта [3]. Необходимо выбрать лучшую площадку для строительства аэропорта с точки зрения выделенных критериев. Комиссия по выбору постройки аэропорта предварительно отобрала из нескольких возможных три альтернативных варианта площадок – А1, А2, А3. Было выявлено три основных критерия, влияющих на принятие решения о выборе площадки для строительства: 1 – стоимость строительства, 2 – время в пути от аэропорта до центра города, 3 – количество жителей, подвергающихся шумовым воздействиям. При решении задачи используется МАИ для поддержки процесса принятия решений.
2.3. Этапы МАИ
Этап 1. Построение иерархической структуры задачи многомерного выбора.
В общем случае простейшей трехуровневой иерархии структура имеет вид Рис.1.
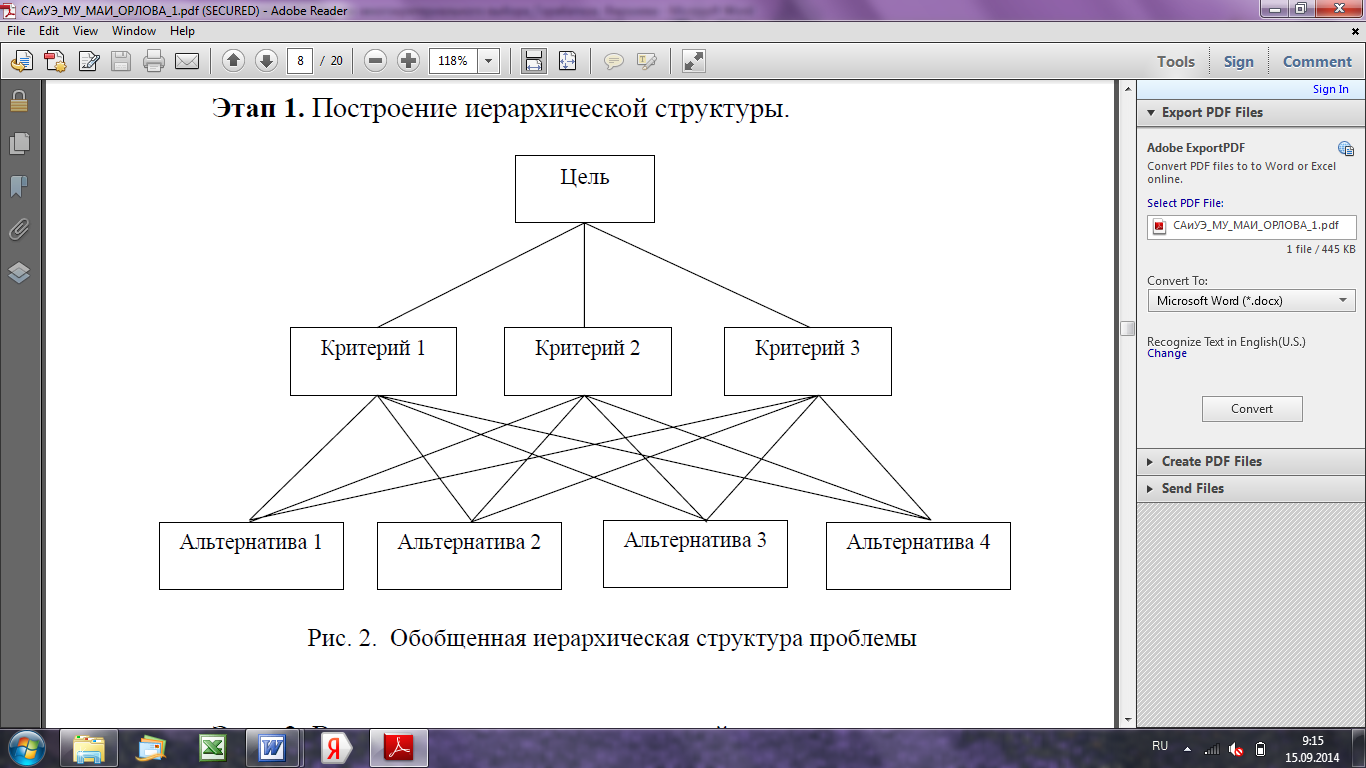
Рис. 1. Обобщенна иерархическая структура проблемы
Этап 1. Структуризация.
Структуру решаемой задачи можно представить в виде иерархической структуры, показанной на Рис. 2.
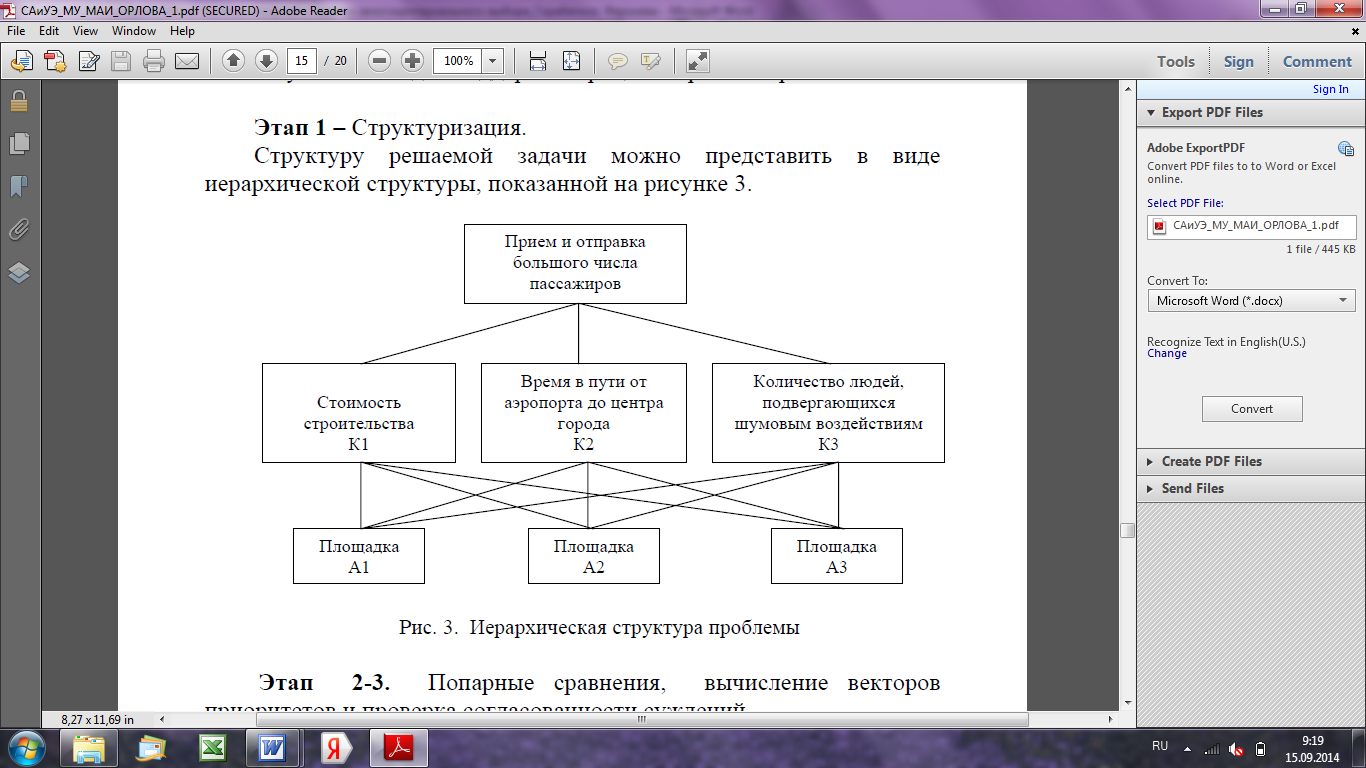
Рис. 2. Иерархическая структура проблемы
Этап 2. Выполнение попарных экспертных сравнений элементов каждого уровня иерархий.
Рассмотрим элементы С1, С2, …, Сnнекоторого зафиксированного уровня иерархи. Мы хотим определить веса ѡ1, ѡ2, …,ѡn влияния этих элементов на некоторый элемент вышестоящего уровня. Основным инструментом оценки влияния является матрица чисел по шкале отношений 1, …, 9 (табл. 1), представляющих суждения о парных сравнениях. Для представления приоритетов в МАИ выбран собственный вектор, принадлежащий наибольшему собственному значению указанной матрицы
А. Обозначим через
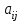 число (бал), соответствующее значимости (предпочтения) элемента Сi по сравнению с элементом Сj данного уровня иерархии по влиянию Сi, Сj на фиксированный элемент вышестоящего уровня (например К1 на Рис. 2):
число (бал), соответствующее значимости (предпочтения) элемента Сi по сравнению с элементом Сj данного уровня иерархии по влиянию Сi, Сj на фиксированный элемент вышестоящего уровня (например К1 на Рис. 2):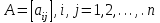 . (5)
. (5)Матрица А с содержательной точки зрения будет согласованной по оценкам при введении условия
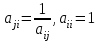 . (6)
. (6)С математической точки зрения это условие наделяет матрицу А свойством обратносимметричной матрицы. На главой диагонали матрицы А стоят 1.
Если оценки попарных сравнений известны точно, т.е. оценки основаны на экспериментальных измерениях, то
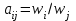 , (7)
, (7)т.е. веса влияния элементов известны.
Например, если взвешиваются два предмета: С1=305,2 и С2=244,2, тогда отношение
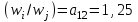 означает, что предмет С1 в 1,25 раз тяжелее предмета С2.
означает, что предмет С1 в 1,25 раз тяжелее предмета С2.Для случая экспериментального измерения весов ѡ1, ѡ2, …,ѡi,…, ѡn сравниваемых элементов на уровне иерархии согласованность считается полной, естественно, с точностью до погрешности измерительных приборов или расчетных методик. При экспертной оценке отношений (7) согласованность суждений и соответственно матрицы А будет не полной. Значит нужно разработать некоторую числовую меру отклонения согласованности матрицы А от идеальной (см. ниже формулу отношения согласованности (9)).
Теперь рассмотрим подробнее содержательный смысл требования согласованности в МАИ.
В МАИ под согласованностью суждений подразумевается не просто традиционное требование транзитивности предпочтений [3]: если например, для индивидуума яблоки предпочтительнее апельсинов, а апельсины предпочтительнее бананов, то яблоки должны быть предпочтительнее бананов.
Схематически это можно записать так:
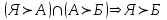 .
.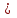 – знак предпочтения элемента в отношении двух элементов; ∩ – знак пересечения множеств (совместности).
– знак предпочтения элемента в отношении двух элементов; ∩ – знак пересечения множеств (совместности). В МАИ транзитивность наделяется количественными отношениями. Например, если яблоки в 2 раза предпочтительнее апельсин ( по цене), а апельсины предпочтительнее бананов в 3 раза, то яблоки должны быть в 6 раз предпочтительнее бананов. Именно это автор МАИ Саати называет числовой (кардинальной) согласованностью предпочтений. Несогласованность означает отсутствие пропорциональности, которое может нарушить транзитивность.
МАИ не только показывает наличие несогласованности отдельных сравнений, но и дает численную оценку того, как сильно нарушена согласованность для всей рассматриваемой задачи.