Файл: Формулировка проблемы.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.12.2023

Просмотров: 197

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



В (8) умножение производится по правилу скалярного произведения векторов.

Например, для матрицы суждений Ас.1 из таблицы 2 получим:
.
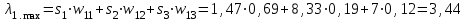Максимальные собственные значения всех матриц суждения 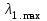, , 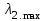, 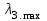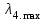приведены соответственно в таблицах 2, 3, 4 и 5.

Этап 5. Определение индексов согласованности и отношений согласованности для матриц суждений.

В общем случае под согласованностью понимается то, что при наличии основного (базового) массива необработанных данных все другие данные логически могут быть получены из них. Или другими словами, отношения элементов всей матрицы А не должны быть противоречивыми.

Из теории МАИ известно, что идеальная согласованность положительной обратносимметричной матрицы эквивалентна требованию

.

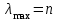Заметим, что 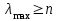всегда верно, поэтому

.

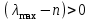Тогда степень согласованности матрицы суждений можно оценить мерой, называемой индексом согласованности (ИС)

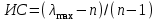. (9)

Знаменатель 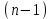– это число всех возможных парных сравнений данного элемента в фиксированной строке i для квадратной матрицы n-го порядка.

Следовательно, ИС имеет смысл отклонения от абсолютной согласованности, приходящегося на одно парное сравнение.

Вводится критерий, называемый отношением согласованности (ОС):
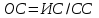, (10)
где СС – индекс случайной согласованности (СС).

СС определяется путем задания оценок по шкале отношений для случайно выбранных суждений 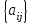при парных сравнениях и соответствующих им обратных величин для матрицы А. Значения СС в теории МАИ заранее вычислены и представлены в таблице 7.
Таблица 7

Случайная согласованность для случайных матриц


Порядок матрицы n
1
2
3
4
5
6
7
8
9
10

Случайная согласованность СС
0
0
0,58
0,9
1,12
1,24
1,32
1,41
1,45
1,49


Приемлемая величина ОС – порядка 10% или менее. Если ОС выходит из этих пределов, то ЛПР должно провести более глубокие исследования задачи и проверить свои суждения, т.е. назначение величин в матрице парных сравнений.

В качестве примера приведем оценки для матрицы суждений Ас.1из таблицы 2:

;

.

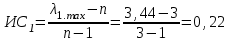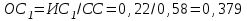Величины значения индекса согласованности и отношений согласованности для матриц суждений Ас.1, Ас.2, Ас.3, Ас.4 показаны соответственно в таблицах 2, 3, 4 и 5.
Замечание. Формально отношения согласованности ОС1=0,378 для матрицы Ас.1, ОС3=0,31 для матрицы Ас.3 и ОС4=0,26 для матрицы Ас.4 являются неприемлемыми, т.е. уровень их согласованности очень мал. Требуется, чтобы ОС было меньше 0,1. Однако исправление указанных матриц суждения, а значит и всей задачи мы делать не будем, поскольку рассматриваемая задача носит учебный характер.
Этап 6. Синтез приоритетов уровней.

В математической теории иерархий разработан метод оценки воздействия уровня на соседний вышестоящий уровень путем композиции соответствующего вклада (приоритетов) элементов данного уровня по отношении к каждому элементу соседнего верхнего уровня. Композиция распространяется снизу-вверх. В принципе, можно рассматривать также распространение композиции сверху-вниз.

Математически «композиция» отображается оператором умножения. Как известно [3], в математической логике операция умножения отображает совместное действие сомножителей.

Приоритеты синтезируются, начиная со второго уровня вниз. Локальные приоритеты (приоритеты альтернатив А1, А2, А3 по каждому критерию) перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии критериями на которые воздействует этот элемент. Процедура продолжается до самого нижнего уровня. В формализованном виде процедура синтеза приоритетов имеет следующий вид.

Общий вектор приоритетов взаимного влияния уровня 3 альтернатив (А1
, А2, А3) и уровня 2 критериев (К1, К2, К3) на общую цель (уровень 1) равен:

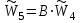, (11)

где В – матрица компонент нормированных векторов приоритетов альтернатив первого снизу уровня (см. таблицы 2, 3 и 4); – нормированный вектор приоритета критериев второго уровня (таблица 5).

В (11) умножение производится по правилам умножения матрицы на вектор:

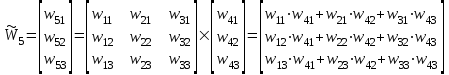. (12)

Для нашего примера:
.
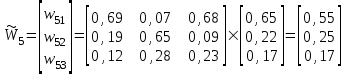Этап 7. Выбор оптимально альтернативы.

Алгоритм оптимального выбора прост:

.

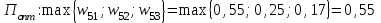Таким образом, алгоритм оптимального многокритериального выбора приводит к выбору площадки А1 для строительства аэропорта, так как ей соответствует наибольшее значение компоненты вектора общего приоритета

.

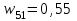Достоинством метода анализа иерархий является направленность на сравнение реальных альтернатив. Метод может применятся в тех случаях, когда эксперты не могут дать абсолютной оценки альтернатив по критериям, а пользуются более слабыми сравнительными измерениями.
3. Ограничения на область применимости метода анализа иерархий
Как и любой метод, даже весьма эффективной, МАИ имеет свои недостатки и ограничения.

Недостатки является возможный неприемлемый уровень согласованности матриц суждений (ОС>0,1), что требует их пересмотра.

Ограничения на область применения содержатся в аксиомах, сформулированных самим автором МАИ Т. Саати:

  1. Обратная симметричность – основная характеристика парных сравнений. Для матрицы парных сравнений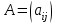 интенсивность предпочтения над 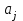обратна интенсивности предпочтения 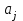над .

  2. Гомогенность (однородность), характеризующая свойство людей сравнивать объекты не слишком отличающиеся друг от друга. Гомогенность существенна для сравнения объектов одного порядка, так как человеческий разум склонен допускать большие ошибки при сравнении несопоставимых элементов.


Пример. Сравнение качества жилья для жителей среднего класса по разным критериям (удаленность от центра, уровень шума, удельная площадь, загрязненность воздуха и др.) соответствует аксиоме гомогенности, а сравнение жилья для жителей разных классов (среднего класса и крупных бизнесменов) – некорректно в смысле гомогенности.

Как быть в этих случаях? Элементы для попарного сравнения в МАИ располагают в отдельные кластеры сравнимых размеров (по числу элементов) и МАИ применяется отдельно к каждому кластеру. Кластерный анализ может быть применен для выявления группы экспертов однородных оценок.


  1. Зависимость нижнего уровня от непосредственно примыкающего к нему высшего уровня.

  2. Результат анализа по МАИ может отражать ожидания экспертов только в том случае, если эти ожидания правильно воспроизведены в иерархи, т.е. все альтернативы и критерий их выбора содержатся в иерархии (их достаточно много) и формализованы в виде согласованной матрицы суждений А. Это не предполагает ни рациональности процесса, ни того, что процесс может приспосабливаться только к рациональной точке зрения. Многие ожидания людей иррациональны.



4. Вопросы для самоподготовки:


  1. Цель метода анализа иерархий (МАИ).

  2. Область применения МАИ.

  3. Ограничения для МАИ.

  4. В чем состоят основные достоинства МАИ?

  5. Как строится иерархия в МАИ (пояснить на конкретном примере)?

  6. Как устроена шкала парных сравнений в МАИ?

  7. Какие условия накладываются на матрицу парных сравнений для различных иерархий в аспекте обеспечения согласованности экспертных оценок?

  8. Какими математическими свойствами обладают матрицы оценок парных сравнений?

  9. Как рассчитываются компоненты вектора приоритетов на анализируемом уровне иерархии?

  10. Как нормируются компоненты вектора приоритетов?

  11. По какому критерию оценивается согласованность матриц суждений по парным сравнениям? Что делать, если уровень согласования недостаточный?

  12. Что такое «идеальное» согласование?

  13. Что такое собственное число λ матрицы и принадлежащий этому собственному числу собственный вектор матрицы?

  14. Как определяется оптимальная альтернатива многокритериального выбора в МАИ?

  15. Как проверить устойчивость полученного решения?


5. Порядок выполнения практического задания

Смотрите также файлы