Замечание. В простейшей версии МАИ считается, что элементы в каждой группе иерархии (называемой уровнем, кластером, стратой) независимы между собой, но все они влияют на каждый элемент другого (вышестоящего) уровня. Таким образом, общая задача многокритериального выбора сводится к задаче оценки влияния уровней иерархи (снизу-вверх либо сверху-вниз).
Теперь обратимся к расчетам для нашего примера.

1. 
   Зафиксируем нижний (третий) уровень иерархи Рис. 2, содержащий элементы А1, А2, А3 альтернативных площадок для строительства аэропорта. Зафиксируем также один элемент К1 – стоимость строительства на уровне 2 иерархии.
   

Примечание: в МАИ можно формировать матрицу парных сравнений на основе любой шкалы отношений, применяемой для измеряемых свойств сравниваемых объектов. В этом случае экспертная оценка заменяется отношением двух соответствующих измерений. Новая шкала (собственный вектор), которая выводится из матрицы парных сравнений, содержащий оценки реальных измерений, будет эквивалентна той, которую можно получить путем нормирования соответствующих измерений.

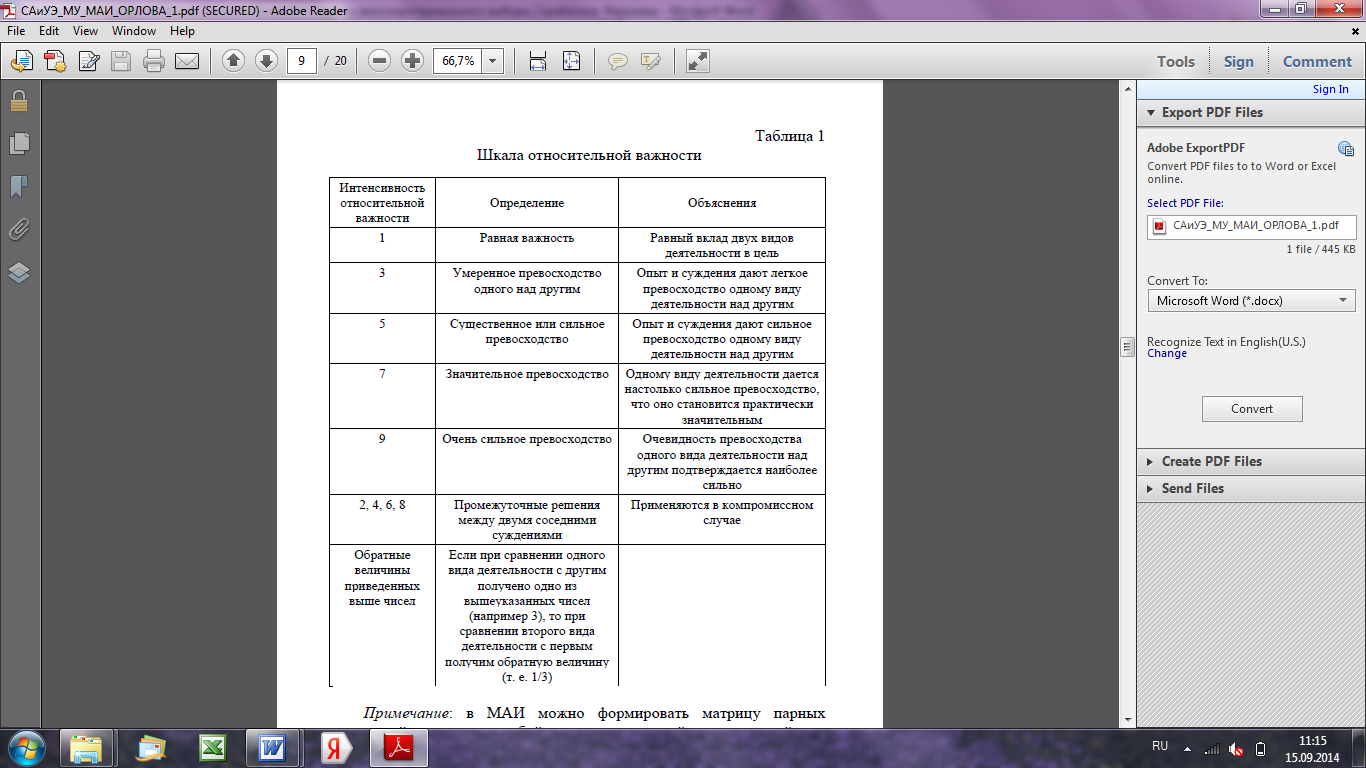
Таблица 1

Шкала относительной важности



Матрица экспертных оценок влияния элементов А1, А2, А3 на элемент К1 второго уровня иерархии показана в таблице 2 (выделено темным цветом). В таблице 2 приведены также расчетные величины для определения максимального собственного значения 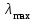и главного собственного вектора 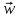полученной матрицы А (алгоритм расчета этих величин описан в этапе 3 алгоритма в таблице 6).

Аналогично получены матрицы парных сравнений элементов А1, А2, А3 относительно критерия К2 (таблица 3) и критерия К3 (таблица 4).


Таблица 2

Матрица А_С.1 парных сравнений альтернатив по первому критерию

Стоимость производства К1	А1	А2	А3	Компоненты собственного вектора W1	Нормализованные компоненты собственного вектора приоритетов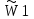
А1	1	7	3	2,76	0,69
А2	1/7	1	3	0,76	0,19
А3	1/3	1/3	1	0,48	0,12
Сумма по столбцу СВ	1,47	8,33	7	4
λmax=3,44; ИС=0,22; ОС=0,379.

---

Таблица 3

Матрица А_С.2 парных сравнений альтернатив по второму критерию

Стоимость производства К2	А1	А2	А3	Компоненты собственного вектора W2	Нормализованные компоненты собственного вектора приоритетов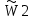
А1	1	1/7	1/5	0,31	0,07
А2	7	1	3	2,76	0,65
А3	5	1/3	1	1,18	0,28
Сумма по столбцу СВ	13	1,47	4,2	4,25
λmax=3,04; ИС=0,22; ОС=0,03.

Таблица 4

Матрица А_С.3 парных сравнений альтернатив по третьему критерию

Стоимость производства К3	А1	А2	А3	Компоненты собственного вектора W3	Нормализованные компоненты собственного вектора приоритетов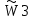
А1	1	5	5	2,93	0,68
А2	1/5	1	1/5	0,34	0,09
А3	1/5	5	1	1	0,23
Сумма по столбцу СВ	1,4	11	6,2	4,27
λmax=3,37; ИС=0,18; ОС=0,31.

---

Аналогично строиться матрица парных сравнений для второго уровня иерархий, элементами которого являются критерии К1, К2, К3. Эта матрица показана в таблице 5 (выделено темным цветом).

Таблица 5

Матрица А_С.4 парных сравнений критериев

	К1	К2	К3	Компоненты собственного вектора W4	Компоненты нормализованного собственного вектора приоритетов элементов второго уровня (критериев)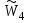
К1	1	5	3	2,47	0,65
К2	1/5	1	3	0,848	0,22
К3	1/3	1/3	1	0,48	0,13
Сумма	1,53	6,33	7	3,8
λmax=3,297; ИС=0,15; ОС=0,26.

Этап 3. Определение вектора приоритетов.

В качестве вектора приоритетов для каждого уровня иерархии принят нормализованный главный собственный вектор матрицы попарных сравнений. Для расчета этих векторов используется приближенный метод 4 из [1] оценки через средние геометрические.

Собственный вектор обеспечивает упорядочение приоритетов. Чем больше i-я компонента СВ, тем больше влияние i-го элемента в комплексе всех элементов анализируемого уровня иерархии на выделенный элемент С вышестоящего уровня.

Для нижнего уровня альтернатив (площадок для строительства А1, А2, А3) алгоритм расчета собственного вектора, относящийся к матрице парных сравнений из таблицы 2, показан в таблице 6. В таблице 2 показан также результат расчета – нормализованный собственный вектор

---

.

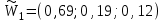
Аналогично рассчитывается нормализованные собственные векторы для матриц парных сравнений А_с.2 и А_с.3 из таблиц 3 и 4.

Получены оценки: 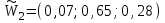; 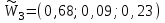, которые отражены в таблицах 3 и 4.

Для второго уровня иерархии, включающего критерии К1, К2 и К3, оценка нормализованного собственного вектора, характеризующие его приоритеты этого уровня по влиянию на единственный элемент верхнего (первого) уровня, т.е. цель выбора, производится по описанному выше алгоритму. Для матрицы парных сравнений А_с.4 из таблицы 5, получены данные расчета: .

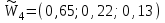Таким образом, все векторы приоритетов для второго и третьего уровней иерархии получены.
Этап 4. Определение максимальных собственных значений и степени согласованности матриц парных сравнений.

Прежде чем перейти к синтезу оптимальной альтернативы с учетом всех элементов второго и третьего уровней иерархии, нужно убедиться в достаточном уровне согласованности всех матриц суждений А_с.1, А_с.2, А_с.2, А_с.4. Для этого нужно вычислить максимальные собственные значения этих матриц. В теории МАИ приводится следующий алгоритм [1] расчета . Сначала суммируется каждый столбец суждений, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца – на вторую компоненту и т.д. Затем полученные числа суммируются: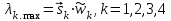
, (8)
где k – номер матрицы парных сравнений (суждений); 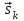– вектор-строка столбцовых сумм матрицы суждений с номером k; 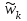– нормализованный собственный главный вектор матрицы суждений А_с.

---

_k, принадлежащий наибольшему собственному значению .


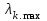Таблица 6

Матрица парных сравнений альтернатив по первому критерию К1

К1	А1	А2	А3	Компоненты собственного вектора	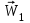Компоненты нормализованного вектора приоритетов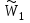
А1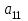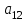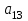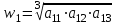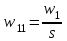
А2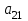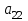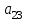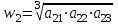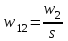
А3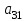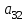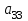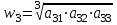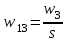
Сумма по столбцам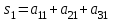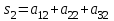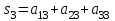

---

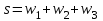Смотрите также файлы

• Загрузите результат Индивидуального практического задания. 45 баллов, слушатель Рыжкова Алина Олеговна Преподаватель Веселко Елизавета Владимировна.rtf

• Учебное пособие по выполнению практических занятий по Основам технологии машиностроения.pdf

• Реферат Профессиональноприкладная физическая подготовка.docx

• Операторов и диспетчеров системы обеспечения вызова экстренных.pdf

• Проектирование редуктора вертолёта.docx