Файл: Курсовая работа термодинамические и кинетические особенности пиролиза углеводородов.docx
Добавлен: 03.12.2023
Просмотров: 133
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
r k
k,обр
gст gст ,
k
где
— стандартная мольная энергия гиббса образования вещества k(справочная величина, 298 K).найти стандартную мольную энергию гиббса реакции при 298 K можно по формуле
r (298) k
k,обр,298
gст
gст .
к
для расчета
при другой, отличной от 298 K темпера- туре Тможно использовать соотношение gcт
hст
T
sст .
r (T)
r (T)
r (T)
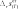
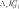
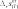при этом значения и должны быть известны. имеются и другие способы расчета . gст go o
r
k k
ksk(T).
T pk T pk
интегрирование уравнения приводит к следующему выраже- нию:
r (T)
r (298)
T
r (298)
T cст (T)
kr r p
T
gcт
gст
-
sст
298
-
k
298
dTdT.
после интегрирования и преобразования полученного выра- жения путем объединения числовых слагаемых, включающих тем- пературу в определенной степени в коэффициенты, получим более простое выражение
r r
298
gст (T) hст
T sст
T aM
bM
cM
cM ],
r
298
r
r
r
r
2
o
1
2
где
lnT 298 1 Mo ;
298 T
T 298 2982 M;
2 2T 1
T2 2982 2983 M;
6 2 3T 2
1 1 2 1 M2 .
2T 2298
298T
коэффициенты
рассчитанные для разных температур, сведены в справочные таблицы. Этот метод расчета стандартной мольной энергии гиббса реакции называется мето- дом темкина — Шварцмана.для проведения курсовой работы разработаны программы, которые позволяют быстро рассчитать величину стандартной мольной энергии гиббса реакции и величину константы равнове- сия при различных температурах. необходимые для расчета спра- вочные материалы приведены в прил. 3.
найденное значение величин стандартных мольных энергий гиббса позволит определить, какая из четырех предложенных реакций наиболее вероятна.
рассмотрим подробнее, от каких факторов и каким образом зависят величина константы равновесия и величина равновесного выхода продукта.
запишем определительное выражение для константы химиче- ского равновесия в логарифмическом виде:
r
ln Kp
gст
r
.
RT
чтобы получить уравнение зависимости логарифма кон- станты равновесия от температуры, удобно использовать уравне- ние гиббса — гельмгольца:
G
T H
T T2 .
p
в этом уравнении связаны между собой изменения энергии гиббса в результате какого-либо процесса и изменение энтальпии в результате этого процесса. запишем данное уравнение в симво- лах мольных величин, рассматривая в качестве процесса химиче- скую реакцию
gст
r hст
T
r.
(2.3)
2
T p T
разделив каждую из частей уравнения (2.3) на −Rи учтя определительное выражение для константы равновесия, получим
ln Kp
r
hст
r .
(2.4)
T p
RT2
дифференциальное уравнение (2.4) исторически называют уравнением изобары вант-гоффа или просто уравнением изобары химической реакции.
проанализируем это уравнение:
-
если стандартная мольная теплота реакции (или стандарт- ное мольное изменение энтальпии в ходе протекания реакции) не равна нулю, то можно утверждать, что константа химического равновесия будет зависеть от температуры. причем она может как увеличиваться с ростом температуры, так и уменьшаться. -
если стандартная мольная теплота реакции равна нулю, то константа химического равновесия данной реакции не зависит от температуры.
r
при интегрировании уравнения (2.4) обычно делают допуще- ние о том, что в небольших обычно исследуемых диапазонах тем- ператур изменение стандартной мольной энтальпии реакции будет несущественным, т. е. можно принять, что Δ hст = const.
интегрирование приводит к уравнению вида
r
dln Kp
p
hст dT
r .
R T2
hст 1
ln Kr
r const.
R T
(2.5)
из анализа уравнения (2.5) видно, что зависимость натураль- ного логарифма константы равновесия от обратной температуры будет линейной, и в этом случае по угловому коэффициенту этой прямой линии можно определить величину стандартной мольной энтальпии реакции.
величины констант равновесия для газовых реакций, записан- ные через мольные доли, а также константы равновесия для жид- ких растворов (через любые концентрационные шкалы) зависят от давления.
воспользуемся логарифмическим видом определительного выражения для константы равновесия
r
ln KN
go
r
.
RT
возьмем частную производную по давлению от этого выраже- ния при постоянной температуре:
ln KN
r
1
go
r
vo
r.
(2.6)
p T RT p T RT
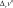
уравнение (2.6) представляет собой зависимость константы равновесия реакции от давления. если то давление не влияет на константу равновесия. если т. е. объем увели- чивается за счет реакции, то из (2.6) следует, что с увеличением давления константа уменьшается. если т. е. объем умень- шается за счет реакции, то с увеличением давления константа увеличивается.знание константы равновесия реакции позволяет рассчитать состав равновесной смеси, т. е. определить максимально возмож- ный, или теоретический, выход желаемого продукта. для этого необходимо решить уравнение закона действия масс (или закона химического равновесия). в предположении идеального поведе- ния газов этот закон запишется
pkr
Kp k ,
(2.7)
k
r [ p]
где под знаком произведения расположены величины, относящи- еся к состоянию равновесия; причем давление выражено как отно- шение парциального давления к единице размерности давления — в виде безразмерной величины.
парциальное давление каждого участника реакции по закону дальтона
n
p pN p nk .
k k
k
k