Файл: Курсовая работа термодинамические и кинетические особенности пиролиза углеводородов.docx

Скачать файл (0,15Мб)

Заказать решение

ВУЗ: Не указан

Категория: Курсовая работа

Дисциплина: Не указана

Добавлен: 03.12.2023

Просмотров: 135

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

если теперь выразить числа молей всех компонентов через начальные количества и глубину реакции, то при известном общем давлении в системе и известной величине константы равновесия получится одно уравнение с одной неизвестной величиной — глу- биной реакции.

__p_^^k^r

^n  

_^vkr

K^p __

__k,о kr __.

(2.8)

^r_[ p] _

^k_ⁿk,о ^^^kr_

Можно также получить уравнения, связывающие величину константы равновесия реакции в другой переменной степенью термической диссоциации.

термическая диссоциация — это распад исходного вещества под действием температуры. рассмотрим, например, реакцию

A ⇄ 2B + C.

степень термической диссоциации — это отношение числа продиссоциировавших молекул исходного вещества к начальному числу молекул этого вещества

__Число продиссоциировавших молекул исходного вещества _n_A_ _.

Начальное число молекул исходного вещества

ⁿA,o ⁿo

отсюда легко найти связь между глубиной химической реак- ции и степенью термической диссоциации:

 n_о,

где n₀ относится к исходному веществу, которое в реакции терми- ческой диссоциации обычно записано с единичным стехиометри- ческим коэффициентом.

для любого реактанта в балансовом соотношении справедливо

n_k n_k_,o _k_r n_k_,o _kn_o.

для исходного вещества в реакции термической диссоциации

n n_o _r n_o(1 ).

запишем данные для расчета равновесного состава:

A	= 2B	+	C
n_k,_о,моль , моль	n_о n_о(1 − )		0 2n_о	0 n₀

о о о о

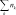= n(1 − ) + 2n  n  n(1 − 2)

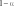
следует обратить внимание на то, что при правильной записи балансовых соотношений введенное нами число молей исходного вещества n₀ должно сократиться. закон химического равновесия имеет вид
2

p² p ^p^N² N

_K^p_ B C ___

_

B C _.

A
^p ^p2

_  ^p _ ^N^A

уравнение для расчета состава равновесной газовой смеси при протекании в ней реакции A ⇄ 2B + C

 _p2

4³

K^p ____

. ^(2.9)

^r ^p

¹^^¹^²^2

степень термической диссоциации можно определить графи- чески по рассчитанной зависимости f () и известному значению константы равновесия или аналитически, если выражение закона химического равновесия не содержит высоких степеней при сте- пени термической диссоциации.

рассмотрим влияние температуры на выход продукта реакции, анализируя уравнение изобары

^ ln K^p^

_r _

__hст

_r _.
(2.10)

 ^^T _p

RT²

повышение температуры ведет к увеличению выхода про- дукта эндотермической реакции (принцип смещения равновесия ле-Шателье). причем чем больше стандартная мольная энтальпия реакции, тем интенсивнее увеличивается выход данного продукта. при введении в систему индифферентного по отношению

к рассматриваемой реакции газа изменятся общее число молей газообразных веществ и, следовательно, мольные доли всех ком- понентов — участников реакции.

k
__n_^

 ⁿk

n_иг.

(2.11)

при этом величина константы равновесия останется неизменной.

k





k

n
^^kⁿ^k

r
K^N

_N^^k

k

k _

___r

k _.

___r

(2.12)

^ⁿk^^^^^^

__k__^ ⁿk^_

_ k  _

если индифферентный газ на влияет на выход продукта.

если введение индифферентного газа увеличивает выход продукта.

если выход продукта уменьшается при введении индифферентного газа.

для определения влияния давления на выход продукта нужно проанализировать уравнение

^ ln K^N^

_r _

  ¹ v^ст.

(2.13)

_p __TRT

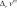если > 0, то с ростом давления равновесный состав системы смещается в сторону уменьшения мольных долей про- дуктов реакции и увеличения мольных долей исходных веществ.

если < 0, то увеличение давления приводит к увеличе- нию выхода продукта.

1 2 3

определение параметров кинетического уравнения

рассмотрим простую реакцию типа

A₁  A₂  продукты.

кинетическое уравнение для такой реакции имеет вид

w kc^¹c^².

(2.14)

V A₁A₂

параметрами кинетического уравнения являются частные

2

1
порядки реакции по компонентам ( и  ), величина константы

скорости реакции (k), величина энергии активации (E_а) и предэк- споненциальный множитель (k_о).

при определении частного порядка реакции по одному из

компонентов необходимо провести реакцию таким образом, чтобы концентрация другого в течение определения не изменялась. Это возможно, если использовать прием, называемый методом изоли-рованияОствальдаили методомизбытков[8].

зададим начальную концентрацию одного из исходных веществ (например, A₁) гораздо большую, чем концентрацию дру- гого: поскольку глубина реакции х одинакова и для первого, и для второго вещества, при сравнении текущих концен- траций первого и второго вещества можно утверждать, что теку- щая концентрация первого вещества практически осталась равной его начальной концентрации и будет и дальше постоянной в тече- ние реакции.

2 2

1 1 1
с_A c_A_,o ₂x; с_A c_A_,o ₁x c_A_,o.
теперь закон скорости можно преобразовать следующим образом:

w k^э^ф (с  x)^²,

V A₂,o 2

где под величиной эффективной константы скорости (k^эф) подра- зумевается произведение константы скорости на начальную кон- центрацию первого компонента в соответствующей степени:

Смотрите также файлы

Факультет Таукен ісі Кафедра г жне Пкоб курсты жмыс.docx

Проект с книгой по жизни Актуальность проектной идеи.docx

Биография Цоя.docx

Занятие 1 Обучающийся Половинкина Екатерина Владимировна Преподаватель Ершова Наталья Николаевна.doc

Программа среднего профессионального образования 44. 02. 02 Преподавание в начальных классах Дисциплина Физическая культура Практическое задание 6.rtf

Файл: Курсовая работа термодинамические и кинетические особенности пиролиза углеводородов.docx

определение параметров кинетического уравнения

Смотрите также файлы

Информация

Списки файлов

Дополнительно