Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Математика.docx
Добавлен: 03.12.2023
Просмотров: 144
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Страховая компания разделяет водителей по трём классам: № 1 (мало рискует), № 2 (рискует средне), № 3 (рискует сильно). Компания предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат классу № 1, 50% - к классу № 2 и 20% - к классу № 3. Вероятность того, что в течение года водитель класса № 1 попадает в одну аварию, равна 0,01, для водителя класса № 2 эта вероятность равна 0,02, а для класса № 3 – 0,08. Найти вероятность того, что водитель, застраховавший свою машину, попадает в аварию в течение года.
Вариант 9. Прибор может собираться из высококачественных деталей и из деталей обычного качества. Известно, что около 40% приборов собирается из высококачественных деталей, при этом вероятность его безотказной работы равна 0,95. Если прибор собран из деталей обычного качества, эта вероятность равна 0,7. Прибор испытывался и работал безотказно. Найти вероятность того, что он собран из высококачественных деталей.
Вариант 10. Пассажир может обратиться за получением билета в одну кассу из трёх. Вероятности обращения в каждую из касс зависят от их месторасположения и равны соответственно 0,2; 0,3; 0,5. Вероятность того, что к моменту прихода пассажира интересующие его билеты будут распроданы, равна для первой кассы 0,3, для второй – 0,4, для третьей – 0,5. Пассажир направился в одну из касс и приобрёл нужный билет. Найти вероятность того, что это была первая касса.
Тема 4. Повторение независимых испытаний. Наивероятнейшее число успехов. Формулы Бернулли, Лапласа, Пуассона.
Вариант 1. Университетом для студенческих общежитий приобретено 5 телевизоров. Для каждого из них вероятность выхода из строя в течение гарантийного рока равна 0,1. Определить вероятность того, что в течение гарантийного срока выйдут из строя: а) ровно один; б) не менее двух; в) не более трех телевизоров.
Вариант 2. В результате систематически проводимого контроля качества изготовляемых предприятием деталей установлено, что брак составляет в среднем 5%. Сколько изготовленных деталей нужно взять, чтобы наиболее вероятное число годных среди них было равно 60 штук?
Вариант 3. Вероятность того, что какой-нибудь абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 300 абонентов. Какова вероятность того, что в течение часа позвонят ровно 4 абонента?
Вариант 4. Вероятность того, что саженец ели прижился и будет расти, равна 0,8. Посажено 400 саженцев. Какова вероятность того, что нормально вырастет: а) ровно 250 деревьев; б) не менее 250 деревьев.
Вариант 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов ровно 5000.
Вариант 6. Вероятность того, что изготовленная рабочим деталь отличного качества, равна 0,8. Найти вероятность того, что среди 100 деталей окажется отличного качества: а) ровно 80 деталей; б) от 70 до 85 деталей; в) не менее 85 деталей.
Вариант 7. В магазине 5 холодильников. Вероятность выхода каждого холодильника из строя в течение года равна 0,2. Найти вероятность того, что в течение года ремонта потребует: а) ровно 4 холодильника; б) не менее 2 холодильников; в) не более 1 холодильника.
Вариант 8. Известно, что в большой партии радиоламп 90% стандартных. Найти вероятности того, что из 300 отобранных радиоламп стандартных окажутся: а)ровно 270; б) от 260 до 275; в) не менее 275.
Вариант 9. Чему равна вероятность наступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 25?
Вариант 10. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятности того, что при 100 выстрелах мишень будет поражена: а) ровно 75 раз; б) от75 до 80 раз; в) не менее 80 раз.
Методические указания к решению задач
Тема 1. Элементы комбинаторики. События и их вероятности,
классический и геометричесий способы подсчета вероятностей
1. При классическом способе подсчета вероятность события А вычисляется по формуле
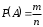, где
все элементарные исходы равновозможны, т.е. ни один из них не является более возможным, чем другой;
n – общее число всех возможных элементарных исходов испытания;
m – число элементарных исходов испытания, благоприятствующих появлению события А.
2. Для подсчета m и n , а также для других целей, часто приходится использовать комбинаторные понятия и формулы.
Пусть имеется n различных объектов (элементов).
а) Расположение их всех в каком-нибудь определенном порядке называется перестановкой из n элементов.
Перестановки, состоящие из одних и тех же элементов, отличаются только порядком их расположения. Число всех возможных перестановок:
,
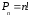где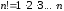
, n=1,2,3,…; 1! = 1, 0! = 1.
б) Расположение некоторых m (m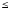
n) из них в определенном порядке называется размещением m элементов из n элементов. Размещения отличаются и составом и порядком элементов. Число всех возможных размещений
.
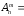
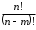
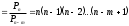Понятно, что при m=n размещение является перестановкой.
в) Если не принимать во внимание порядок элементов в размещении, а учитывать только его состав, то получится сочетание m элементов из n. Сочетания отличаются только составом элементов.
Число всех возможных сочетаний
.
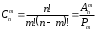3. Геометрические вероятности – вероятности попадания точки в область(отрезок, часть плоскости и т.д.) – применяются, когда элементарные исходы эксперимента могут быть интерпретированы как точки отрезка, фигуры или тела.
Пусть отрезок lсоставляет часть отрезка L. Если предположить, что вероятность попадания точки на отрезок lпропорциональна длине этого отрезка, то вероятность попадания точки на отрезок l определяется равенством
Р = Длина l/ Длина L.
Аналогично определяется вероятность попадания точки в плоскую фигуру g, составляющую часть плоской фигуры G
Р = Площадь g/Площадь G
и вероятность попадания точки в пространственную фигуру
, которая составляет часть фигуры V
Р = Объём /Объём V.
Пример 1. (Варианты 1, 2, 3, 4)
В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение:
Событие А = {извлечены три окрашенных детали}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 3 детали из 15, т.е.
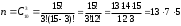
Число исходов, благоприятствующих интересующему нас событию, равно числу способов, которыми можно извлечь 3 детали из 10 окрашенных, т. е.
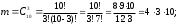
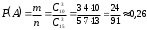
Пример 2. (Варианты 5, 6, 7, 8)
В цехе работают шесть мужчин и четыре женщины. Наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины и четыре мужчины.
Решение:
Событие А= {среди отобранных ровно три женщины}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно выбрать 7 человек из всех работников, цеха, т.е. из 10 человек.
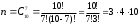
Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди 7 отобранных ровно 3 женщины): трёх женщин можно выбрать из четырёх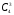
способами; при этом остальные 4 человека должны быть мужчинами. Выбрать же четырех мужчин из шести мужчин можно 
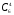способами.
Следовательно,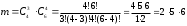
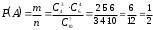
Пример 3. (Варианты 9, 10)
На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадает в кольцо, образованное построенными окружностями.
Р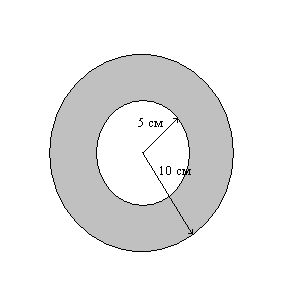
ешение:
Площадь кольца (фигуры g)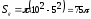
.
Площадь большого круга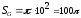
Искомая вероятность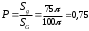
.
Тема 2.Операции над событиями.
Правила сложения и умножения вероятностей
События называются несовместными
, если появление одного из них исключает появление других событий в одном и том же испытании.
Два события называются совместными, если появление одного из них не исключает появление другого события в том же испытании.
Событие В называется независимым от события А, если появление события А не изменяет вероятности события В, т.е.
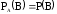, где
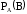- условная вероятность наступления события В, если событие А уже наступило.
1. Сложение вероятностей.
Правило сложения вероятностей совместных событий
Для любых событий А и В
Р(А+В)=Р(А)+Р(В)-Р(АВ), где
Р(А+В) – вероятность появления хотя бы одного из двух событий,
Р(АВ) – вероятность совместного появления двух событий.
Правило сложения вероятностей несовместных событий
Р(А+В)=Р(А)+Р(В).
2. Умножение вероятностей
Правило умножения вероятностей зависимых событий
Для любых событий А и В
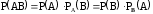, где
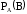- условная вероятность наступления события В, если событие А уже наступило,
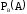- условная вероятность наступления события А, если событие В уже наступило.
Правило умножения вероятностей независимых событий
.
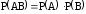Пример 4. (Все варианты)
Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый вопрос, рана 0,9; на второй – 0,7; на третий – 0,8. Найти вероятность того, что студент ответит:
а) только на один вопрос (варианты 1,2,3,7,10)
б) на все вопросы (варианты 7,8)
в) хотя бы на один вопрос (варианты 3,4,6)
г) по крайней мере на два вопроса (варианты 3,9)
д) на два вопроса (варианты 4,5)
Решение:
Пусть событие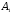
= {студент ответил на первый вопрос},
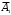= {студент не ответил на первый вопрос},
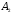={ студент ответил на второй вопрос },
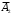={ студент не ответил на второй вопрос },
Вариант 9. Прибор может собираться из высококачественных деталей и из деталей обычного качества. Известно, что около 40% приборов собирается из высококачественных деталей, при этом вероятность его безотказной работы равна 0,95. Если прибор собран из деталей обычного качества, эта вероятность равна 0,7. Прибор испытывался и работал безотказно. Найти вероятность того, что он собран из высококачественных деталей.
Вариант 10. Пассажир может обратиться за получением билета в одну кассу из трёх. Вероятности обращения в каждую из касс зависят от их месторасположения и равны соответственно 0,2; 0,3; 0,5. Вероятность того, что к моменту прихода пассажира интересующие его билеты будут распроданы, равна для первой кассы 0,3, для второй – 0,4, для третьей – 0,5. Пассажир направился в одну из касс и приобрёл нужный билет. Найти вероятность того, что это была первая касса.
Тема 4. Повторение независимых испытаний. Наивероятнейшее число успехов. Формулы Бернулли, Лапласа, Пуассона.
Вариант 1. Университетом для студенческих общежитий приобретено 5 телевизоров. Для каждого из них вероятность выхода из строя в течение гарантийного рока равна 0,1. Определить вероятность того, что в течение гарантийного срока выйдут из строя: а) ровно один; б) не менее двух; в) не более трех телевизоров.
Вариант 2. В результате систематически проводимого контроля качества изготовляемых предприятием деталей установлено, что брак составляет в среднем 5%. Сколько изготовленных деталей нужно взять, чтобы наиболее вероятное число годных среди них было равно 60 штук?
Вариант 3. Вероятность того, что какой-нибудь абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 300 абонентов. Какова вероятность того, что в течение часа позвонят ровно 4 абонента?
Вариант 4. Вероятность того, что саженец ели прижился и будет расти, равна 0,8. Посажено 400 саженцев. Какова вероятность того, что нормально вырастет: а) ровно 250 деревьев; б) не менее 250 деревьев.
Вариант 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух и более пуль, если число выстрелов ровно 5000.
Вариант 6. Вероятность того, что изготовленная рабочим деталь отличного качества, равна 0,8. Найти вероятность того, что среди 100 деталей окажется отличного качества: а) ровно 80 деталей; б) от 70 до 85 деталей; в) не менее 85 деталей.
Вариант 7. В магазине 5 холодильников. Вероятность выхода каждого холодильника из строя в течение года равна 0,2. Найти вероятность того, что в течение года ремонта потребует: а) ровно 4 холодильника; б) не менее 2 холодильников; в) не более 1 холодильника.
Вариант 8. Известно, что в большой партии радиоламп 90% стандартных. Найти вероятности того, что из 300 отобранных радиоламп стандартных окажутся: а)ровно 270; б) от 260 до 275; в) не менее 275.
Вариант 9. Чему равна вероятность наступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 25?
Вариант 10. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятности того, что при 100 выстрелах мишень будет поражена: а) ровно 75 раз; б) от75 до 80 раз; в) не менее 80 раз.
Методические указания к решению задач
Тема 1. Элементы комбинаторики. События и их вероятности,
классический и геометричесий способы подсчета вероятностей
1. При классическом способе подсчета вероятность события А вычисляется по формуле
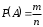, гдевсе элементарные исходы равновозможны, т.е. ни один из них не является более возможным, чем другой;
n – общее число всех возможных элементарных исходов испытания;
m – число элементарных исходов испытания, благоприятствующих появлению события А.
2. Для подсчета m и n , а также для других целей, часто приходится использовать комбинаторные понятия и формулы.
Пусть имеется n различных объектов (элементов).
а) Расположение их всех в каком-нибудь определенном порядке называется перестановкой из n элементов.
Перестановки, состоящие из одних и тех же элементов, отличаются только порядком их расположения. Число всех возможных перестановок:
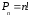,где
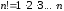, n=1,2,3,…; 1! = 1, 0! = 1.б) Расположение некоторых m (m
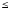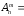
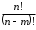
n) из них в определенном порядке называется размещением m элементов из n элементов. Размещения отличаются и составом и порядком элементов. Число всех возможных размещений 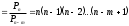.Понятно, что при m=n размещение является перестановкой.
в) Если не принимать во внимание порядок элементов в размещении, а учитывать только его состав, то получится сочетание m элементов из n. Сочетания отличаются только составом элементов.
Число всех возможных сочетаний
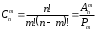.3. Геометрические вероятности – вероятности попадания точки в область(отрезок, часть плоскости и т.д.) – применяются, когда элементарные исходы эксперимента могут быть интерпретированы как точки отрезка, фигуры или тела.
Пусть отрезок lсоставляет часть отрезка L. Если предположить, что вероятность попадания точки на отрезок lпропорциональна длине этого отрезка, то вероятность попадания точки на отрезок l определяется равенством
Р = Длина l/ Длина L.
Аналогично определяется вероятность попадания точки в плоскую фигуру g, составляющую часть плоской фигуры G
Р = Площадь g/Площадь G
и вероятность попадания точки в пространственную фигуру
, которая составляет часть фигуры VР = Объём
/Объём V.Пример 1. (Варианты 1, 2, 3, 4)
В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение:
Событие А = {извлечены три окрашенных детали}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 3 детали из 15, т.е.
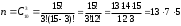
Число исходов, благоприятствующих интересующему нас событию, равно числу способов, которыми можно извлечь 3 детали из 10 окрашенных, т. е.
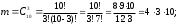
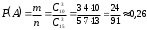
Пример 2. (Варианты 5, 6, 7, 8)
В цехе работают шесть мужчин и четыре женщины. Наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины и четыре мужчины.
Решение:
Событие А= {среди отобранных ровно три женщины}. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно выбрать 7 человек из всех работников, цеха, т.е. из 10 человек.
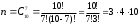
Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди 7 отобранных ровно 3 женщины): трёх женщин можно выбрать из четырёх
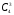способами; при этом остальные 4 человека должны быть мужчинами. Выбрать же четырех мужчин из шести мужчин можно 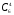способами. Следовательно,
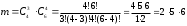
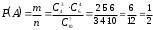
Пример 3. (Варианты 9, 10)
На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадает в кольцо, образованное построенными окружностями.
Р
ешение: Площадь кольца (фигуры g)
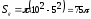.Площадь большого круга
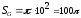
Искомая вероятность
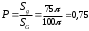. Тема 2.Операции над событиями.
Правила сложения и умножения вероятностей
События называются несовместными
, если появление одного из них исключает появление других событий в одном и том же испытании.
Два события называются совместными, если появление одного из них не исключает появление другого события в том же испытании.
Событие В называется независимым от события А, если появление события А не изменяет вероятности события В, т.е.
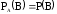, где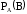 - условная вероятность наступления события В, если событие А уже наступило.1. Сложение вероятностей.
Правило сложения вероятностей совместных событий
Для любых событий А и В
Р(А+В)=Р(А)+Р(В)-Р(АВ), где
Р(А+В) – вероятность появления хотя бы одного из двух событий,
Р(АВ) – вероятность совместного появления двух событий.
Правило сложения вероятностей несовместных событий
Р(А+В)=Р(А)+Р(В).
2. Умножение вероятностей
Правило умножения вероятностей зависимых событий
Для любых событий А и В
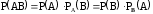, где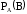 - условная вероятность наступления события В, если событие А уже наступило, 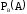- условная вероятность наступления события А, если событие В уже наступило. Правило умножения вероятностей независимых событий
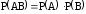.Пример 4. (Все варианты)
Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый вопрос, рана 0,9; на второй – 0,7; на третий – 0,8. Найти вероятность того, что студент ответит:
а) только на один вопрос (варианты 1,2,3,7,10)
б) на все вопросы (варианты 7,8)
в) хотя бы на один вопрос (варианты 3,4,6)
г) по крайней мере на два вопроса (варианты 3,9)
д) на два вопроса (варианты 4,5)
Решение:
Пусть событие
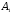= {студент ответил на первый вопрос}, 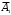= {студент не ответил на первый вопрос}, 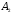={ студент ответил на второй вопрос }, 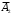={ студент не ответил на второй вопрос },