ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 186
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
слабее вы толкаете качели, тем дольше придётся их раскачивать до заданной амплитуды. Выглядит логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит. Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.
Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна. Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу гипотезу о квантах, высказанную Максом Планком пятью годами ранее.
Электромагнитная энергия излучается и поглощается не непрерывно, а дискретно отдельными порциями — квантами. Энергия кванта пропорциональна частоте излучения:
Cоотношение (3.1) называется формулой Планка, а коэффициент пропорциональности h — постоянной Планка. Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.
Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики. Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией E = hν. Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью c. Каждый фотон монохроматического света, имеющего частоту ν, несёт энергию hν. Фотоны могут обмениваться энергией и импульсом с частицами вещества; в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода. Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и этим объясняется безынерционность фотоэффекта.
Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона hν при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода A по извлечению электрона из вещества и на придание электрону кинетической энергии:
Слагаемое mv2/2 называется максимальной кинетической энергией фотоэлектронов. Почему максимальной? Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине. Ясно, что максимальной кинетическая энергия фотоэлектрона будет в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода. Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности. Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.
Энергия квантовых частиц часто измеряется во внесистемных единицах «электрон-вольтах».
1 электрон-вольт (эВ) = 1.6·10-19 Дж.
Красной границей фотоэффекта называется минимальная частота излучения, при которой всё ещё наблюдается фотоэффект
Таблица 3.1. Значения работы выхода электронов для различных материалов фотокатодов
У большинства чистых металлов «красная граница» лежит в ультрафиолетовой части спектра.
Запирающим (задерживающим) напряжением называется минимальное тормозящее напряжение между анодом вакуумной лампы (фотоэлемента) и фотокатодом, при котором отсутствует ток в цепи этой лампы, т.е. фотоэлектроны не долетают до анода. При таком напряжении кинетическая энергия электронов у катода равна потенциальной энергии электронов у анода
Описание установки
Внешний фотоэффект используется в приборах, которые называются фотоэлементами (ФЭ). В данной работе используется вакуумные фотоэлементы Ф-08 и Ф-13.
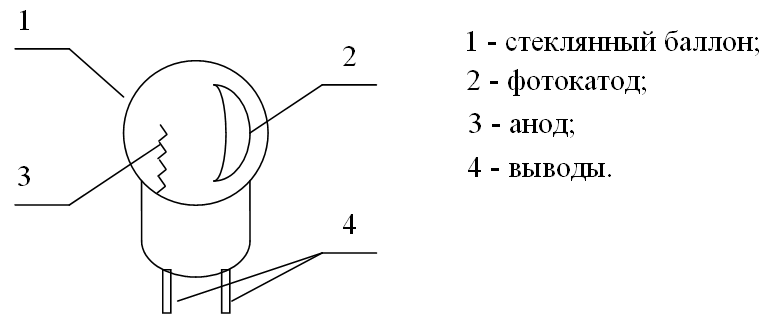
Рис.3.4. Схематичное изображение фотоэлемента
Фотоэлемент Ф-13 измерительный вакуумный с массивным мультищелочным катодом на алюминиевой пластине, с предварительно нанесенным слоем сурьмы.
Оптический вход торцевой
Диаметр катода 27±1 мм
Диаметр колбы без штенгеля, не более 40 мм
Высота фотоэлемента без штырьков 50±2 мм
Область спектральной чувствительности 350 — 700 нм
Спектральная чувствительность на длине волны 600 нм составляет не менее 17 % от максимума, на длине волны 700 нм — не менее 1 % от максимума. Рабочее напряжение 300 В при импульсных потоках излучения и 100 В при постоянном во времени световом потоке. Относительная неравномерность чувствительности катода не превышает ±30 % от его среднего значения. Среднее отклонение фототока от его среднего значения в серии 20 световых импульсов при длительности (3-10) мкс не превышает ±2 % при повторных импульсах, происходящих раз в 60 сек.
Внешний вид экспериментальной установки изображен на рис.3.5.

Рис.3.5. Экспериментальная установка
К корпусу 1, в котором находится источник излучения, прикреплен усилитель фототока, на верхнюю крышку которого устанавливаются сменные фотоприемники с фотоэлементами Ф-8 или Ф-13 (2). При установке фотоприемников их приемное окно совмещают с выходным окном осветителя и закрывают при помощи бленды. 3 - измерительный блок.
Порядок работы
1. Получить у преподавателя или инженера номера фотоэлемента и используемых светофильтров.
Установить на объект исследования фотоприемник с исследуемым фотоэлементом и соединить бленду осветителя с окном фотоэлемента.
2. Включить объект исследования выключателем «СЕТЬ» на его передней панели. Дайте лампе осветителя прогреться в течение 15 минут.
3. Подключите сетевые шнуры измерительного устройства к сети, нажмите тумблер «СЕТЬ» на его задней панели. При этом должен загореться индикатор «ОБРАТНАЯ». На индикаторе вольтметра должны установиться нули (допускается индикация до значения 2 младшего разряда). После пятиминутного прогрева ручками «УСТАНОВКА НОЛЯ» на объекте исследования установить нулевое значение на индикаторе амперметра.
ВНИМАНИЕ! РЕЖИМ РАБОТЫ УСТАНОВКИ ПРЕРЫВИСТЫЙ – ЧЕРЕЗ КАЖДЫЕ 45 МИНУТ РАБОТЫ ПЕРЕРЫВ 15 МИНУТ.
4. Установить необходимый светофильтр.
5. С помощью кнопки «ПРЯМАЯ-ОБРАТНАЯ» выбрать режим измерения обратной вольт-амперной характеристики.
6. Изменяя значения напряжения с помощью кнопок «+» и «-», измерьте вольт-амперную характеристику в обратном направлении. Не забудьте указать знак напряжения и силы тока.
7. Выбрать режим «ПРЯМАЯ» и повторить пп.5,6 для прямой вольтамперной характеристики.
Результаты измерения занести в таблицу 3.2.
Таблица 3.2.
8. Снять прямые и обратные вольт-амперные характеристики с другими светофильтрами и фотоэлементами, согласно Вашему варианту.
По окончании измерений отключить питание установки.
9. Выбрав удобный масштаб, построить на миллиметровой бумаге семейство измеренных вольт-амперных характеристик. Для каждой из них определить токи насыщения и задерживающий потенциал, как показано на рис.3.6. Значения занести в таблицу 3.3. Вычислить работу выхода для каждого фотоэлемента. Используя таблицу 3.1, определить материал катода.
Таблица 3.3.
Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна. Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу гипотезу о квантах, высказанную Максом Планком пятью годами ранее.
Электромагнитная энергия излучается и поглощается не непрерывно, а дискретно отдельными порциями — квантами. Энергия кванта пропорциональна частоте излучения:
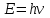 , , 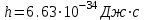 | | (3.1) |
Cоотношение (3.1) называется формулой Планка, а коэффициент пропорциональности h — постоянной Планка. Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.
Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики. Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией E = hν. Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью c. Каждый фотон монохроматического света, имеющего частоту ν, несёт энергию hν. Фотоны могут обмениваться энергией и импульсом с частицами вещества; в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода. Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и этим объясняется безынерционность фотоэффекта.
Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона hν при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода A по извлечению электрона из вещества и на придание электрону кинетической энергии:
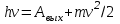 . . | | (3.2) |
Слагаемое mv2/2 называется максимальной кинетической энергией фотоэлектронов. Почему максимальной? Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине. Ясно, что максимальной кинетическая энергия фотоэлектрона будет в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода. Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности. Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.
Энергия квантовых частиц часто измеряется во внесистемных единицах «электрон-вольтах».
1 электрон-вольт (эВ) = 1.6·10-19 Дж.
Красной границей фотоэффекта называется минимальная частота излучения, при которой всё ещё наблюдается фотоэффект
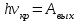 . . | | (3.3) |
Таблица 3.1. Значения работы выхода электронов для различных материалов фотокатодов
| Катод | А вых, эВ | Катод | А вых, эВ |
| Цезий | 1,89 | Серебро | 4,30 |
| Барий | 2,29 | Золото | 4,58 |
| Калий | 2,15 | Платина | 5,30 |
| Алюминий | 4,2 | Медь | 4,46 |
| Сурьма | 4,08-4,56 | Ниобий | 3,99 |
| Натрий | 2,28 | Титан | 3,92 |
| Цинк | 3,74 | Литий | 2,39 |
| | | | |
| | | | |
У большинства чистых металлов «красная граница» лежит в ультрафиолетовой части спектра.
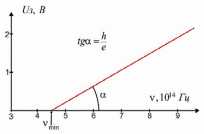 | Когда напряжение на аноде отрицательно, электрическое поле между катодом и анодом тормозит электроны. Анода могут достичь только те электроны, кинетическая энергия которых превышает |eU|. Если напряжение на аноде меньше, чем – Uз, фототок прекращается. Измеряя Uзап, можно графически определить максимальную кинетическую энергию фотоэлектронов, как показано на рис.3.3. |
| Рис.3.3. Зависимость запирающего потенциала Uз от частоты ν падающего света |
Запирающим (задерживающим) напряжением называется минимальное тормозящее напряжение между анодом вакуумной лампы (фотоэлемента) и фотокатодом, при котором отсутствует ток в цепи этой лампы, т.е. фотоэлектроны не долетают до анода. При таком напряжении кинетическая энергия электронов у катода равна потенциальной энергии электронов у анода
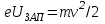 . . | | (3.4) |
Описание установки
Внешний фотоэффект используется в приборах, которые называются фотоэлементами (ФЭ). В данной работе используется вакуумные фотоэлементы Ф-08 и Ф-13.

Рис.3.4. Схематичное изображение фотоэлемента
Фотоэлемент Ф-13 измерительный вакуумный с массивным мультищелочным катодом на алюминиевой пластине, с предварительно нанесенным слоем сурьмы.
Оптический вход торцевой
Диаметр катода 27±1 мм
Диаметр колбы без штенгеля, не более 40 мм
Высота фотоэлемента без штырьков 50±2 мм
Область спектральной чувствительности 350 — 700 нм
Спектральная чувствительность на длине волны 600 нм составляет не менее 17 % от максимума, на длине волны 700 нм — не менее 1 % от максимума. Рабочее напряжение 300 В при импульсных потоках излучения и 100 В при постоянном во времени световом потоке. Относительная неравномерность чувствительности катода не превышает ±30 % от его среднего значения. Среднее отклонение фототока от его среднего значения в серии 20 световых импульсов при длительности (3-10) мкс не превышает ±2 % при повторных импульсах, происходящих раз в 60 сек.
Внешний вид экспериментальной установки изображен на рис.3.5.

Рис.3.5. Экспериментальная установка
К корпусу 1, в котором находится источник излучения, прикреплен усилитель фототока, на верхнюю крышку которого устанавливаются сменные фотоприемники с фотоэлементами Ф-8 или Ф-13 (2). При установке фотоприемников их приемное окно совмещают с выходным окном осветителя и закрывают при помощи бленды. 3 - измерительный блок.
Порядок работы
1. Получить у преподавателя или инженера номера фотоэлемента и используемых светофильтров.
Установить на объект исследования фотоприемник с исследуемым фотоэлементом и соединить бленду осветителя с окном фотоэлемента.
2. Включить объект исследования выключателем «СЕТЬ» на его передней панели. Дайте лампе осветителя прогреться в течение 15 минут.
3. Подключите сетевые шнуры измерительного устройства к сети, нажмите тумблер «СЕТЬ» на его задней панели. При этом должен загореться индикатор «ОБРАТНАЯ». На индикаторе вольтметра должны установиться нули (допускается индикация до значения 2 младшего разряда). После пятиминутного прогрева ручками «УСТАНОВКА НОЛЯ» на объекте исследования установить нулевое значение на индикаторе амперметра.
ВНИМАНИЕ! РЕЖИМ РАБОТЫ УСТАНОВКИ ПРЕРЫВИСТЫЙ – ЧЕРЕЗ КАЖДЫЕ 45 МИНУТ РАБОТЫ ПЕРЕРЫВ 15 МИНУТ.
4. Установить необходимый светофильтр.
5. С помощью кнопки «ПРЯМАЯ-ОБРАТНАЯ» выбрать режим измерения обратной вольт-амперной характеристики.
6. Изменяя значения напряжения с помощью кнопок «+» и «-», измерьте вольт-амперную характеристику в обратном направлении. Не забудьте указать знак напряжения и силы тока.
7. Выбрать режим «ПРЯМАЯ» и повторить пп.5,6 для прямой вольтамперной характеристики.
Результаты измерения занести в таблицу 3.2.
Таблица 3.2.
| фотоэлемент №__, светофильтр № _ | |||||||||
| U, В | | | | | | | | | |
| I, А·10-6 | | | | | | | | | |
8. Снять прямые и обратные вольт-амперные характеристики с другими светофильтрами и фотоэлементами, согласно Вашему варианту.
По окончании измерений отключить питание установки.
9. Выбрав удобный масштаб, построить на миллиметровой бумаге семейство измеренных вольт-амперных характеристик. Для каждой из них определить токи насыщения и задерживающий потенциал, как показано на рис.3.6. Значения занести в таблицу 3.3. Вычислить работу выхода для каждого фотоэлемента. Используя таблицу 3.1, определить материал катода.
Таблица 3.3.
| Светофильтр | 0 | 1 | 2 | 3 | 4 | 5 |
| Фиолетовый | Фиолетовый | синий | Зеленый | желтый | УФ | |
| гр, нм | 380 | 407 | 435 | 546 | 578 | ? |
| σ(гр), м ·10-9 | | | 5,0 | |||
| в, с-1 ·1014 | | | | | | |
| σ(в), с-1 ·1014 | | | | | | |
| Uз, В | | | | | | |
| σП(Uз), В | | | | |||
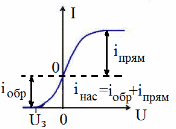 | 10. Для фотоэлемента Ф-13 построить зависимости задерживающего напряжения от частоты падающего света. Считая зависимость линейной, с помощью метода наименьших квадратов вычислить угловой коэффициент и определить значение постоянной Планка h. |
| Рис.3.6. |