Файл: Квантовая оптика.docx

Вопросы и задания для самоконтроля

1. 
   В чём заключается сущность явления фотоэффекта?
   
2. 
   Объясните принцип работы фотоэлемента с внешним фотоэффектом.
   
3. 
   Что такое «красная граница» фотоэффекта? Чем обусловлено её наличие и положение на шкале длин волн?
   
4. 
   Объясните причину различия вольтамперных характеристик в прямом направлении для разных световых потоков.
   

6. 
   При каких условиях возникает ток насыщения? Изобразите вольтамперную характеристику фотоэлемента, включенного в обратном направлении. Объясните ее.
   

ЛАБОРАТОРНАЯ РАБОТА № 4

ИЗУЧЕНИЕ СПЕКТРА АТОМА ВОДОРОДА
И ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ РИДБЕРГА

ЦЕЛЬ РАБОТЫ:

Провести калибровку спектрометра; исследовать спектр атомарного водорода и неона; вычислить постоянную Ридберга.

КРАТКАЯ ТЕОРИЯ

Оптические свойства атомов определяются состоянием валентных электронов. Согласно современным представлениям, электроны в атомах могут находиться лишь в неких стационарных состояниях, которым соответствуют строго определенные дискретные значения энергии, называемые энергетическими уровнями. В простейшем случае, в атоме водорода имеется единственный электрон, который является валентным электроном.

Состояние атома в квантовой механике описывается волновой функцией φ_n, его энергия Е_n. В случае простейшего атома – атома водорода, состоящего из протона и электрона, квантовая механика позволяет получить точные решения уравнения Шредингера

,

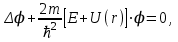(4.1)

где m – масса электрона, Е – полная энергия, 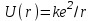- энергия взаимодействия электрона с ядром, е – заряд электрона, 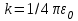, 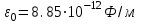- электрическая постоянная. Решения уравнения (4.1) для атома водорода являются набором дискретных уровней энергии. Для связанных состояний (Е_n<0):

,

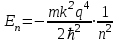(4.2)

где

---

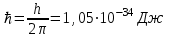
, n =1,2,3,…- главное квантовое число.

С ростом числа n уровни энергии атома сближаются, в пределе при 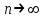дискретный спектр приближается к непрерывному, а квантовая система к классической. Это и есть принцип соответствия Бора, который позволяет выразить энергию электронов в атоме через фундаментальные постоянные. Для простоты Бор принял, что в атоме водорода электроны вращаются вокруг протона по окружности радиусом r с циклической частотой ω:

.

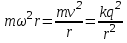(4.3)

Согласно правилу квантования момента импульса электрона в атоме:

.

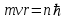(4.4)

Решение уравнений (4.3) и (4.4) дает выражение для радиусов круговых орбит электронов в атоме водорода:

.

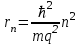(4.5)

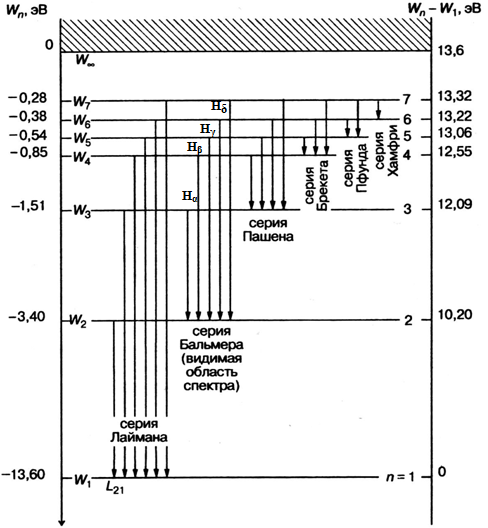
Рис.4.1. Энергетическая диаграмма атома водорода
Таким образом, при переходе атома водорода из состояния n₂ c энергией Е₂ в состояние n₁ с энергией Е₁ действует правило частот Бора:

,

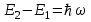(4.6)

то есть испускается фотон с частотой ω и длиной волны λ

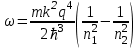,		(4.7)
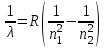.		(4.8)

Здесь введено обозначение 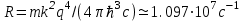- постоянная Ридберга. Формула (4.8) называется формулой Бальмера-Ритца. В этой формуле с увеличением n₂ и n₁ разность между волновыми числами

---

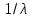уменьшается, стремясь при 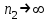к предельному значению 0. При этом линии сближаются, и уменьшается их интенсивность.

Совокупность длин волн (или частот), излучаемых телом, называют спектром излучения этого тела. Как мы видим, вследствие квантования энергетических уровней электронов в атомах атомарные спектры излучения состоят из дискретного набора длин волн (частот). Такие спектры называются линейчатыми. Совокупность спектральных линий, т.е. длин волн или частот, соответствующих переходам на один и тот же энергетический уровень n₁ образует серию линий:

- совокупность переходов в основное состояние (n₁ =1) образует серию Лаймана;

- переходы в состояние с n₁ =2 образуют серию Бальмера;

- переходы в состояние с n₁ =3 образуют серию Пашена.

Визуально мы можем наблюдать только серию Бальмера: для водорода – n₁ = 2, n₂ = 3,4,5…(рис.4.1).

Выполнение работы:

Внешний вид установки для определения спектральных характеристик атомов показан на рис. 4.2. На оптической скамье 1 соосно установлены источник света (поочередно ртутная, неоновая и водородная лампы) и приемник-анализатор 3 с микрометрическим винтом 4, задающим исследуемую длину волны, и окуляром для наблюдения 5.

Измерения с помощью микрометрического винта

Микрометрический винт имеет два отсчетных устройства. Первое отсчетное устройство состоит из шкалы с ценой деления 0,500 мм, нанесенной на стебле 1 , как показано на рис.4.3, и указателя, которым является торец барабана 2. Второе отсчетное устройство состоит из шкалы, с ценой деления 0,010 мм, нанесенной на конусной поверхности барабана 2, и указателя в виде продольного штриха, нанесенного на стебле 1. Шаг микровинта S = 0,500 мм, следовательно, одному обороту микровинта и жестко скрепленного с ним барабана соответствует линейное перемещение торца барабана на одно деление, равное 0,500 мм. Круговая шкала барабана имеет число делений n=50 и следовательно, поворот барабана с микровинтом на одно деление относительно продольного штриха стебля 1 рис.2 будет соответствовать величине 0.500/50 10 мкм. Это цена деления прибора. Для проведения измерений производят отсчеты по двум отсчетным устройствам и суммируют их. Примеры отсчета показаны на рис.4.3.

---

Рис.4.2. Вид установки для измерения постоянной Ридберга

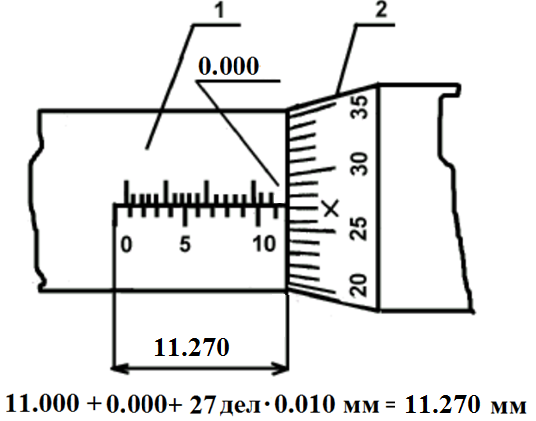Рис.4.3.Измерение с помощью микрометрического винта

---

Для проведения измерений необходимо провести калибровку спектрометра по известному спектру ртутной лампы.

1. 
   Установить на оптической скамье ртутную лампу в качестве источника излучения. С помощью регулировочных винтов добиться одинакового уровня источника излучения и бленды фотоприемника. Установить головку микрометрического винта в ближайшее к корпусу положение (УФ область спектра).
   
2. 
   Осторожно вращая головку винта и наблюдая в окуляр, найти максимум крайней фиолетовой линии спектра, отвечающий 404.7 нм. Записать положение винта в таблицу 4.1.
   

Таблица 4.1. Градуировка спектрометра

№	Цвет линии	Длины волн линий спектра ртути λ, нм	Положение микрометрического винта d, мкм
1	Фиолетовый	404.7
2	Фиолетовый	407.8
3	Сине-фиолетовый	435.8
4	Голубой	491,6
5	Зеленый	546.0
6	Желтый	576.9
7	Желтый	579.0
8	Оранжевый	623.4
9	Красный	671.0
10	красный	690.7

3. 
   Повторить измерения для указанных в таблице линий спектра.
   
4. 
   Считая калибровочную зависимость λ(d) линейной функцией, определить ее угловой коэффициент и свободный член с помощью метода наименьших квадратов. Выбрав достаточно крупный масштаб, построить зависимость λ(d) на миллиметровой бумаге формата А4.
   

Наблюдение спектра неоновой лампы

---