ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 311
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
a 3 составляет 99,73%, т.е. практически все значения нормально распределённой случайной величины находятся в этом интервале. Это свойство нормального распределения называется “правилом 3“.
Для характеристики случайной величины на практике пользуются выборкой. Выборкой называется последовательность независимых одинаково распределённых случайных величин. Выборка, пронумерованная в порядке возрастания, т.е. x1, x2 ... xn, называется вариационным рядом. Сами значения x называются вариантами, а n - объёмом выборки. В табл. 10.1 приведены основные характеристики, используемые для описания выборки.
Табл. 10.1.
Основные характеристики, используемые для описания выборки
Чем меньше число степеней свободы (n-1), тем в большей степени выборочные характеристики отличаются от характеристик случайной величины. Для характеристики выборок малых объёмов (n < 30), взятых из нормально распределённых генеральных совокупностей, используют
распределение Стьюдента (t-распределение), представляющее собой распределение случайной величины t
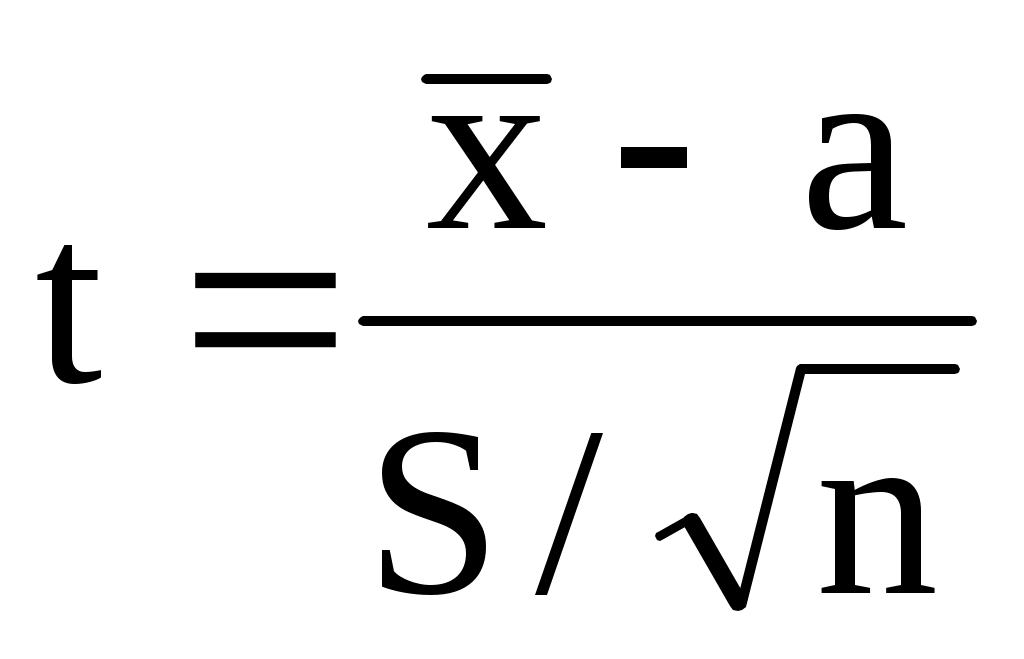(или 
)
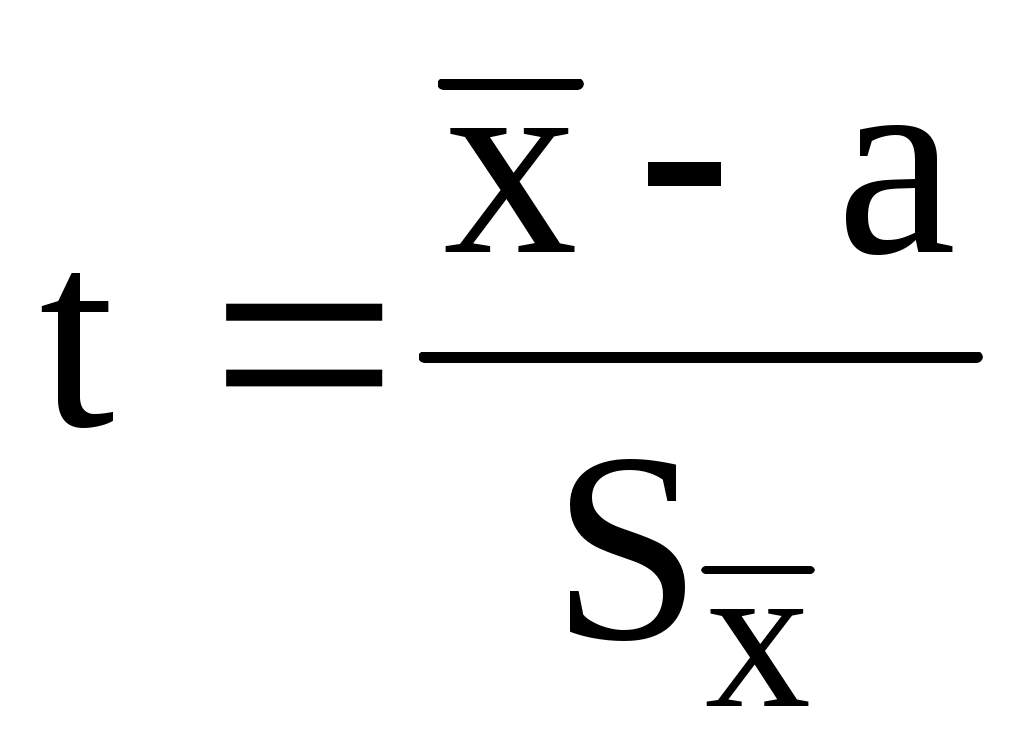Данное распределение зависит только от объёма выборки и не зависит от неизвестных параметров a и . При
распределение Стьюдента переходит в стандартное нормальное распределение.
Распределение Стьюдента можно использовать для расчёта доверительного интервала выборочного среднего (в том случае, если выборка имеет нормальное распределение). Доверительным интервалом называется интервал, вероятность попадания значений случайной величины в который равна принятой нами доверительной вероятности 1-, где - уровень значимости (в аналитической практике = 0,05). Неизвестное математическое ожидание с вероятностью 1- попадёт в интервал:
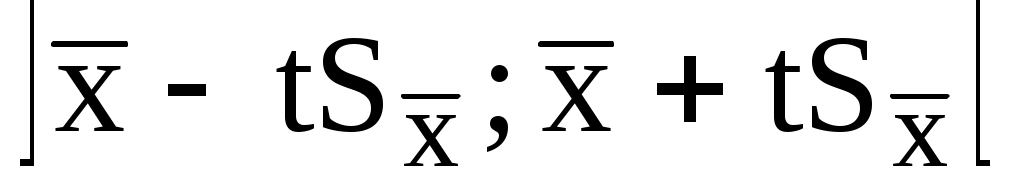
Например, если = 0,05 и f = 5, то доверительный интервал для выборочного среднего равен 2,57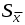
.
10.6. Пример статистической обработки результатов измерений. Исключение промахов
Процесс анализа многостадиен. Каждая стадия вносит определённый вклад в неопределённость окончательного результата. Рассмотрим простейший вариант статистической обработки последней стадии анализа - измерения аналитического сигнала.
Пример 10.4. При измерении рН раствора с помощью рН-метра получены следующие результаты 4,32; 4,35; 4,36; 4,98; 4,38; 4,34. Провести статистическую обработку полученных результатов.
Перед началом статистической обработки необходимо проверить, не содержат ли полученные результаты грубых погрешностей. Измерения, в которых обнаружены такие погрешности, должны быть исключены. Их нельзя использовать при дальнейшей статистической обработке результатов. Существует несколько способов исключения грубых погрешностей. Для исключения промахов при работе с выборками малого объёма (n = 4 - 10) можно воспользоваться величиной Q-критерия. Для выборок больших объёмов можно использовать, например, «правило 3» - если значение отличается от среднего более, чем на 3 стандартных отклонения, то его можно считать промахом.
Экспериментальное значение Q-критерия рассчитывают по следующим формулам:
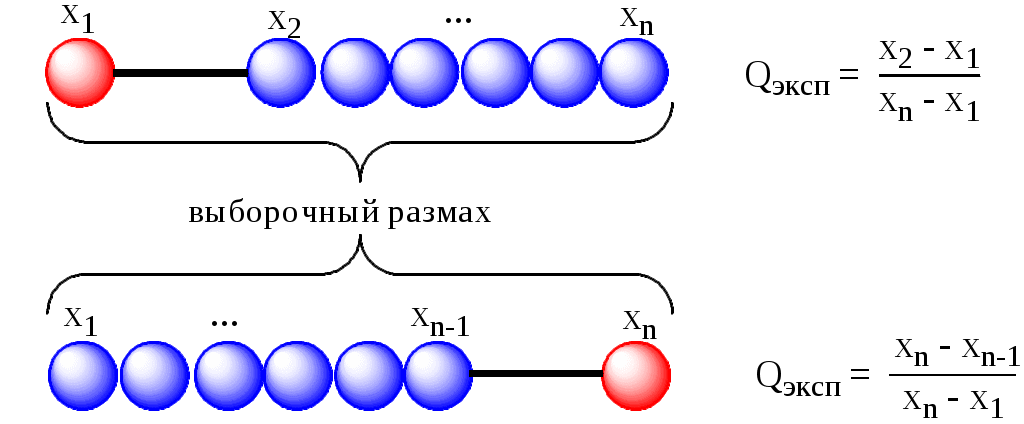
Полученное значение сравнивают с критической (табличной) величиной для Q-критерия. Если оно превышает последнюю, то проверяемый результат является промахом и его необходимо исключить из дальнейших расчётов.
Преобразуем выборку, приведенную в примере 10.4, в вариационный ряд:
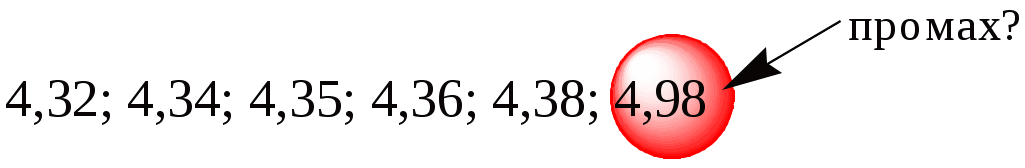
Последнее значение является явно подозрительным. Рассчитаем для него величину Q
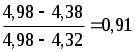
Для n= 6 и P = 0,90 Qкрит = 0,48. Следовательно, результат рН = 4,98 является промахом и его необходимо исключить.
При обработке оставшихся данных с помощью формул, представленных в табл. 10.1, получены следующие результаты: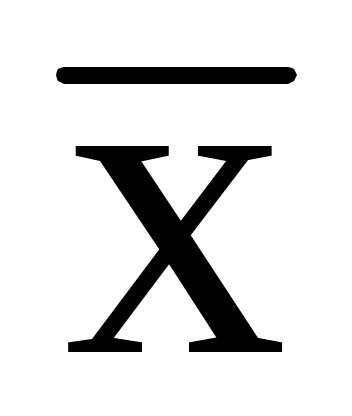
= 4,35; 
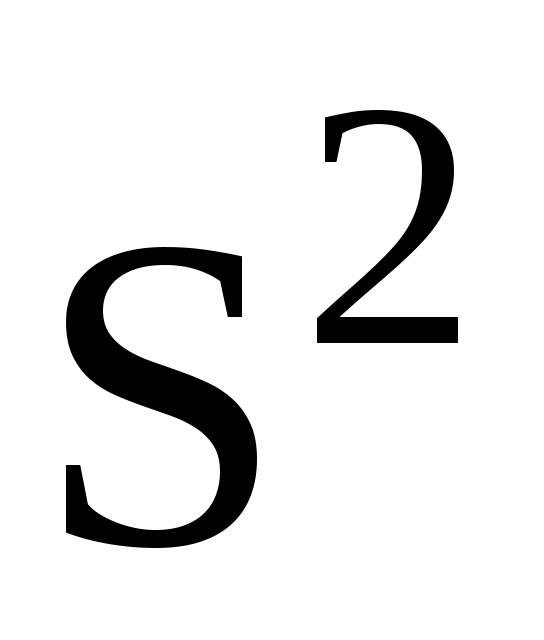= 5,0010-4; 
= 2,2410-2;
= 1,0010-2;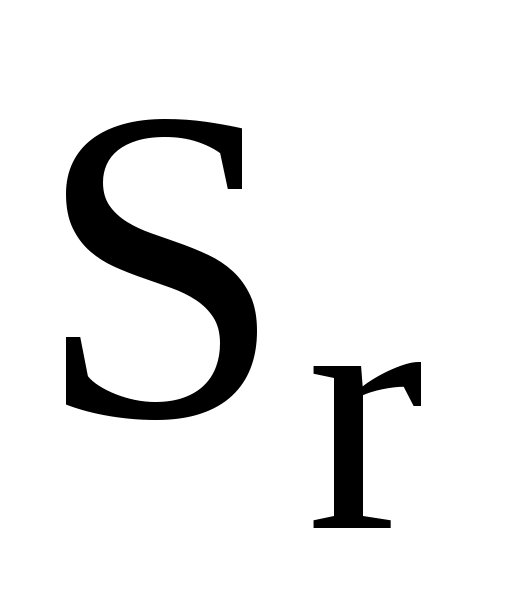 
= 5,1510-3; 
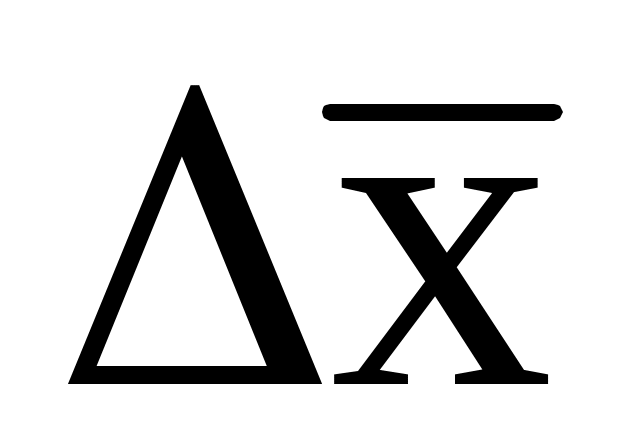(=0,05) = 0,03. Таким образом, рН = 4,350,03.
Обратите внимание, что окончательный результат среднего значения рН содержит столько же значащих цифр (3), сколько их присутствует в исходных данных. Величина, характеризующая доверительный интервал среднего, имеет столько же десятичных знаков (2), сколько и само среднее. Если бы мы привели в качестве результата, что-нибудь вроде 4,35000,028, то это было бы неверно.
10.7. Основные характеристики методики анализа
Основными характеристиками методики анализа являются воспроизводимость и правильность, предел обнаружения, границы определяемых содержаний и чувствительность.
Воспроизводимость(precision) - степень близости друг к другу независимых результатов измерений при оговоренных условиях.
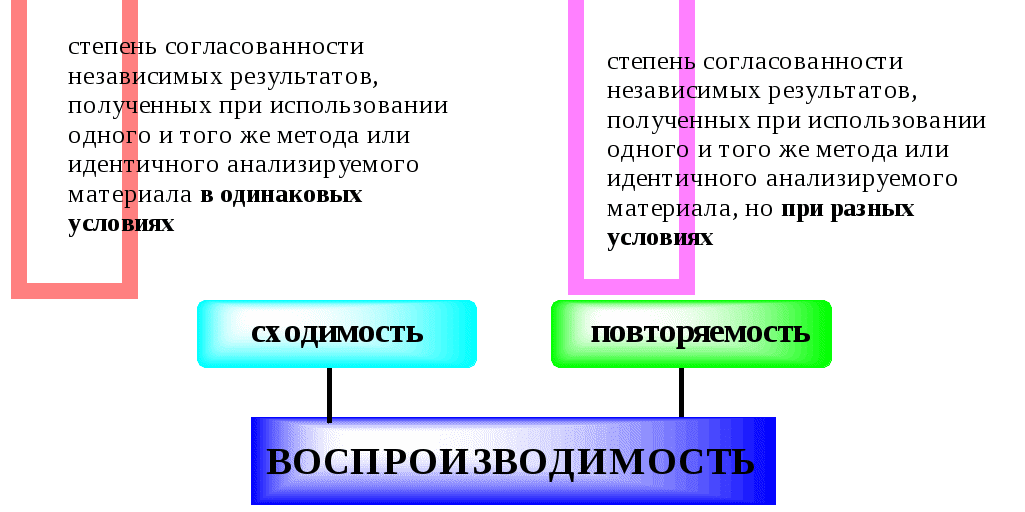
Количественно воспроизводимость (или невоспроизводимость) удобнее всего описывать с помощью относительного стандартного отклонения. Чем больше величина Sr, тем воспроизводимость хуже.
Для сравнения воспроизводимости результатов двух серий анализа используют F-критерий (критерий Фишера).
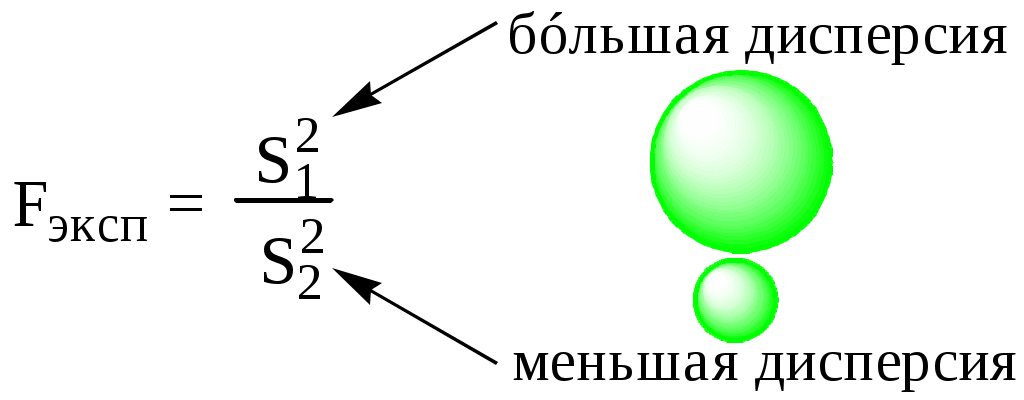
Полученное значение сравнивают с критическим (табличным) при выбранном уровне значимости (обычно 0,05 или 0,01) и числе степеней свободы (f1,f2). При конкурирующей гипотезе «одна из дисперсий больше второй дисперсии» используют уровень значимости (односторонняя постановка задачи), при конкурирующей гипотезе «дисперсии не равны между собой» используется уровень значимости /2 (двухсторонняя постановка задачи). Если Fэксп < Fкрит, то считается, что дисперсии двух серий анализа отличаются незначимо.
Пример 10.5. При измерении рН раствора один студент получил результат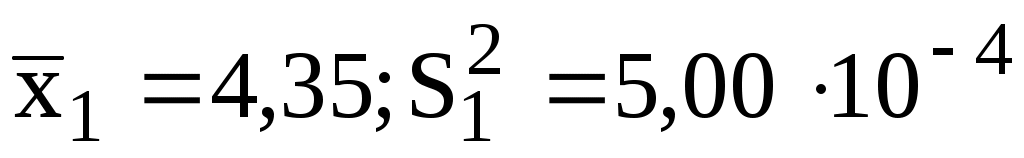
, а второй студент - 
. Определить, различаются ли полученные данные по воспроизводимости, если каждый студент провёл по 5 параллельных измерений.
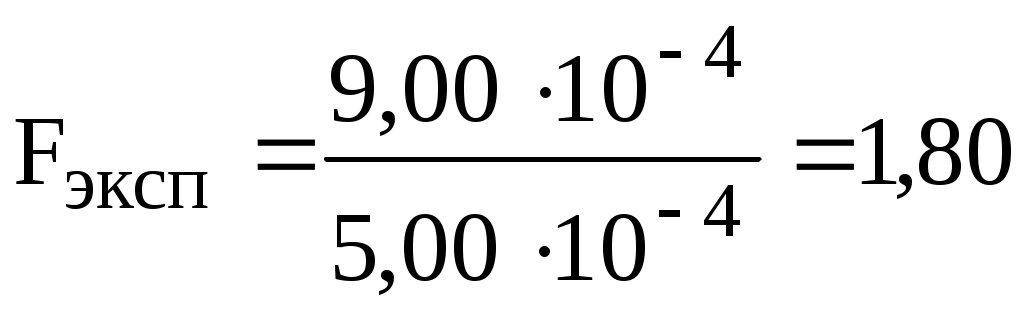
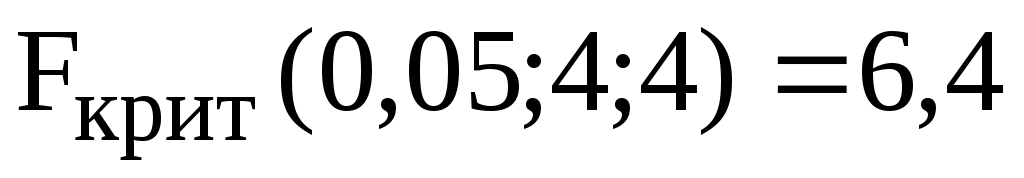
Поскольку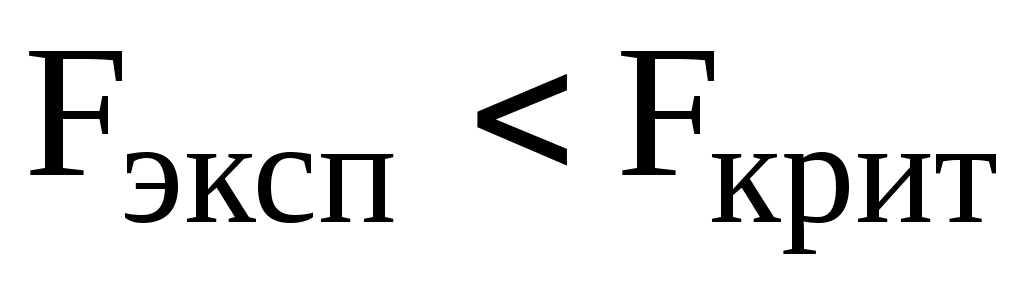
, можно сделать вывод, что полученные результаты имеют одинаковую воспроизводимость.
Правильность (accuracy) - отсутствие систематического смещения результатов от действительного значения, отсутствие систематической погрешности
.
Правильность, в отличие от воспроизводимости, является качественной характеристикой. Результат анализа может быть правильным либо неправильным.
Для проверки правильности используют следующие приёмы:
варьирование величины пробы;
способ «введено-найдено»;
анализ образца различными методами - метод, выбранный для сравнения, должен быть независимым (иметь другой принцип) и давать заведомо правильные результаты;
анализ стандартных образцов.
При проверке правильности результатов анализа приходится сравнивать средние результаты, полученные исследуемым и стандартным методом. Если установлено, что отличия между дисперсиями статистически незначимы, то это можно сделать следующим образом.
Вначале рассчитывают средневзвешенное значение дисперсии:
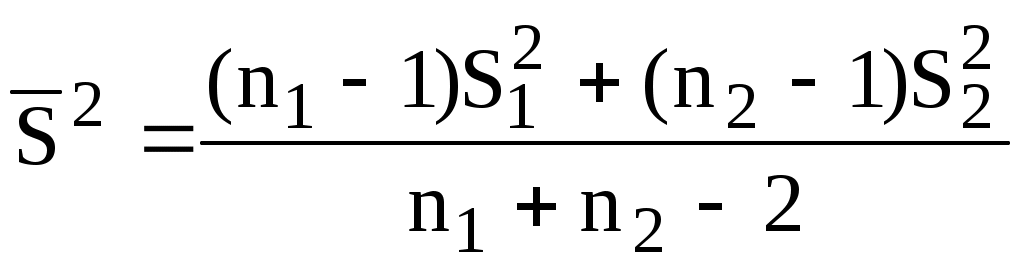
Затем рассчитывают экспериментальное значение t-критерия:
Если число параллельных опытов в каждой серии равно, то
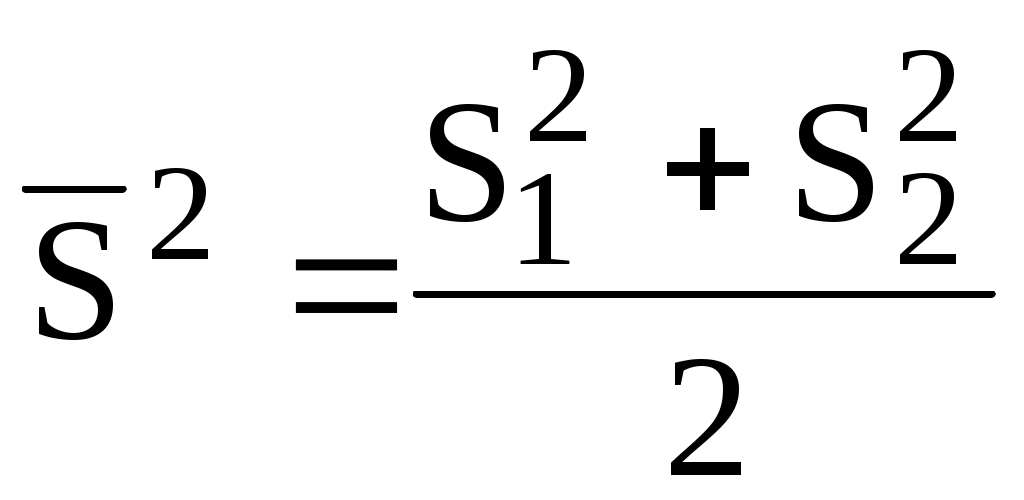
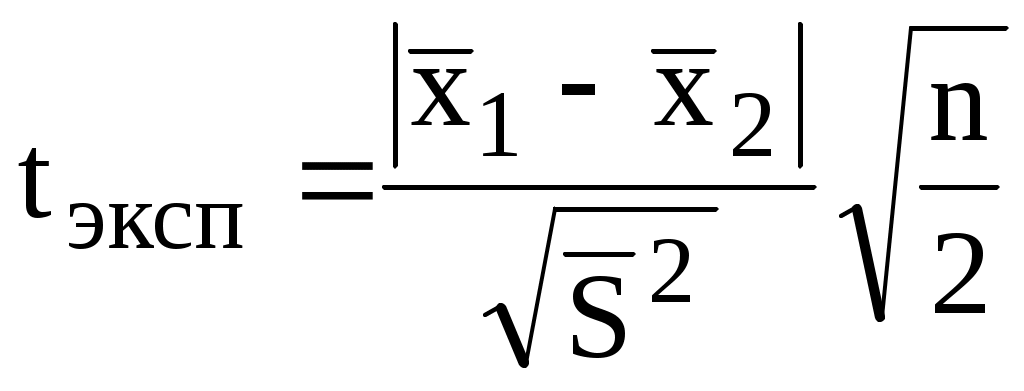
Полученное значение t сравнивают с критическим значением t для выбранного уровня значимости и числа степеней свободы f = n1 + n2 - 2. При односторонней постановке задачи используется уровень значимости , при двусторонней постановке задачи - /2. Если tэксп < tкрит, то средние результаты не имеют значимых различий.
Пример 10.6.Определить отличаются ли средние результаты, полученные в примере 10.5.
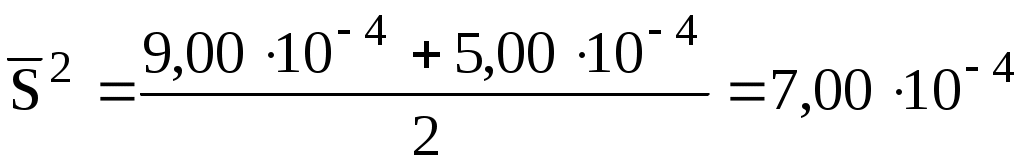
Критическое значение tдля = 0,05 и f = 8 равно 2,31 (табл.2.2). Так как tэксп > tкрит, то различие между средними результатами статистически значимо - среднее значение рН, полученное первым студентом больше, чем полученное вторым студентом.
Для характеристики случайной величины на практике пользуются выборкой. Выборкой называется последовательность независимых одинаково распределённых случайных величин. Выборка, пронумерованная в порядке возрастания, т.е. x1, x2 ... xn, называется вариационным рядом. Сами значения x называются вариантами, а n - объёмом выборки. В табл. 10.1 приведены основные характеристики, используемые для описания выборки.
Табл. 10.1.
Основные характеристики, используемые для описания выборки
| Характеристика | Определение понятия | Расчётная формула |
| выборочное среднее | сумма всех значений серии наблюдений, делённая на число наблюдений |  |
| выборочная дисперсия (исправленная) | сумма квадратов отклонений, делённая на число степеней свободы. Число степеней свободы f = n-1 - число переменных, которые могут быть присвоены произвольно при характеристике данной выборки |  |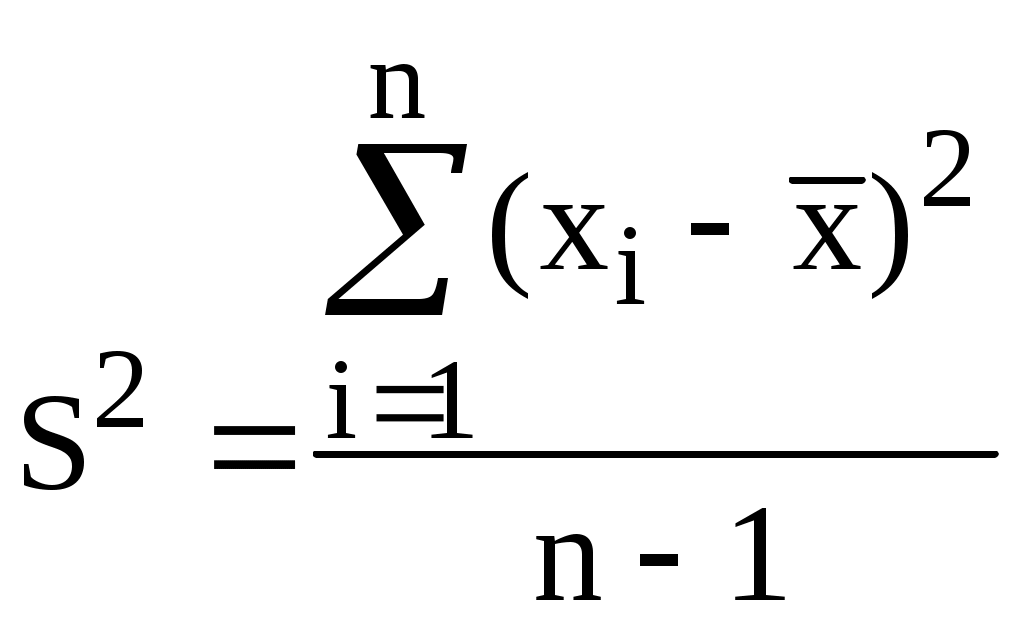
| выборочное стандартное отклонение | положительный квадратный корень из выборочной дисперсии |  |
| стандартное отклонение выборочного среднего | отношение выборочного стандартного отклонения к положительному квадратному корню из числа наблюдений |  |
| относительное стандартное отклонение | отношение выборочного стандартного отклонения к выборочному среднему |  |
Чем меньше число степеней свободы (n-1), тем в большей степени выборочные характеристики отличаются от характеристик случайной величины. Для характеристики выборок малых объёмов (n < 30), взятых из нормально распределённых генеральных совокупностей, используют
распределение Стьюдента (t-распределение), представляющее собой распределение случайной величины t
(или )Данное распределение зависит только от объёма выборки и не зависит от неизвестных параметров a и . При
распределение Стьюдента переходит в стандартное нормальное распределение.Распределение Стьюдента можно использовать для расчёта доверительного интервала выборочного среднего (в том случае, если выборка имеет нормальное распределение). Доверительным интервалом называется интервал, вероятность попадания значений случайной величины в который равна принятой нами доверительной вероятности 1-, где - уровень значимости (в аналитической практике = 0,05). Неизвестное математическое ожидание с вероятностью 1- попадёт в интервал:
Например, если = 0,05 и f = 5, то доверительный интервал для выборочного среднего равен 2,57
.10.6. Пример статистической обработки результатов измерений. Исключение промахов
Процесс анализа многостадиен. Каждая стадия вносит определённый вклад в неопределённость окончательного результата. Рассмотрим простейший вариант статистической обработки последней стадии анализа - измерения аналитического сигнала.
Пример 10.4. При измерении рН раствора с помощью рН-метра получены следующие результаты 4,32; 4,35; 4,36; 4,98; 4,38; 4,34. Провести статистическую обработку полученных результатов.
Перед началом статистической обработки необходимо проверить, не содержат ли полученные результаты грубых погрешностей. Измерения, в которых обнаружены такие погрешности, должны быть исключены. Их нельзя использовать при дальнейшей статистической обработке результатов. Существует несколько способов исключения грубых погрешностей. Для исключения промахов при работе с выборками малого объёма (n = 4 - 10) можно воспользоваться величиной Q-критерия. Для выборок больших объёмов можно использовать, например, «правило 3» - если значение отличается от среднего более, чем на 3 стандартных отклонения, то его можно считать промахом.
Экспериментальное значение Q-критерия рассчитывают по следующим формулам:
Полученное значение сравнивают с критической (табличной) величиной для Q-критерия. Если оно превышает последнюю, то проверяемый результат является промахом и его необходимо исключить из дальнейших расчётов.
Преобразуем выборку, приведенную в примере 10.4, в вариационный ряд:
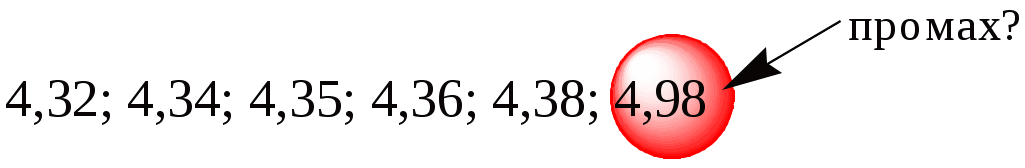
Последнее значение является явно подозрительным. Рассчитаем для него величину Q
Для n= 6 и P = 0,90 Qкрит = 0,48. Следовательно, результат рН = 4,98 является промахом и его необходимо исключить.
При обработке оставшихся данных с помощью формул, представленных в табл. 10.1, получены следующие результаты:
= 4,35; = 5,0010-4; = 2,2410-2; = 1,0010-2; = 5,1510-3; (=0,05) = 0,03. Таким образом, рН = 4,350,03.Обратите внимание, что окончательный результат среднего значения рН содержит столько же значащих цифр (3), сколько их присутствует в исходных данных. Величина, характеризующая доверительный интервал среднего, имеет столько же десятичных знаков (2), сколько и само среднее. Если бы мы привели в качестве результата, что-нибудь вроде 4,35000,028, то это было бы неверно.
10.7. Основные характеристики методики анализа
Основными характеристиками методики анализа являются воспроизводимость и правильность, предел обнаружения, границы определяемых содержаний и чувствительность.
Воспроизводимость
Воспроизводимость(precision) - степень близости друг к другу независимых результатов измерений при оговоренных условиях.
Количественно воспроизводимость (или невоспроизводимость) удобнее всего описывать с помощью относительного стандартного отклонения. Чем больше величина Sr, тем воспроизводимость хуже.
Для сравнения воспроизводимости результатов двух серий анализа используют F-критерий (критерий Фишера).
Полученное значение сравнивают с критическим (табличным) при выбранном уровне значимости (обычно 0,05 или 0,01) и числе степеней свободы (f1,f2). При конкурирующей гипотезе «одна из дисперсий больше второй дисперсии» используют уровень значимости (односторонняя постановка задачи), при конкурирующей гипотезе «дисперсии не равны между собой» используется уровень значимости /2 (двухсторонняя постановка задачи). Если Fэксп < Fкрит, то считается, что дисперсии двух серий анализа отличаются незначимо.
Пример 10.5. При измерении рН раствора один студент получил результат
, а второй студент - . Определить, различаются ли полученные данные по воспроизводимости, если каждый студент провёл по 5 параллельных измерений. Поскольку
, можно сделать вывод, что полученные результаты имеют одинаковую воспроизводимость. Правильность
Правильность (accuracy) - отсутствие систематического смещения результатов от действительного значения, отсутствие систематической погрешности
.
Правильность, в отличие от воспроизводимости, является качественной характеристикой. Результат анализа может быть правильным либо неправильным.
Для проверки правильности используют следующие приёмы:
варьирование величины пробы;
способ «введено-найдено»;
анализ образца различными методами - метод, выбранный для сравнения, должен быть независимым (иметь другой принцип) и давать заведомо правильные результаты;
анализ стандартных образцов.
При проверке правильности результатов анализа приходится сравнивать средние результаты, полученные исследуемым и стандартным методом. Если установлено, что отличия между дисперсиями статистически незначимы, то это можно сделать следующим образом.
Вначале рассчитывают средневзвешенное значение дисперсии:
Затем рассчитывают экспериментальное значение t-критерия:
Если число параллельных опытов в каждой серии равно, то
Полученное значение t сравнивают с критическим значением t для выбранного уровня значимости и числа степеней свободы f = n1 + n2 - 2. При односторонней постановке задачи используется уровень значимости , при двусторонней постановке задачи - /2. Если tэксп < tкрит, то средние результаты не имеют значимых различий.
Пример 10.6.Определить отличаются ли средние результаты, полученные в примере 10.5.
Критическое значение tдля = 0,05 и f = 8 равно 2,31 (табл.2.2). Так как tэксп > tкрит, то различие между средними результатами статистически значимо - среднее значение рН, полученное первым студентом больше, чем полученное вторым студентом.