Файл: Практическая работа в форме практической подготовки 15.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Ответ:
Пример 3
По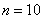 равноточным измерениям найдено исправленное среднее квадратическое отклонение
равноточным измерениям найдено исправленное среднее квадратическое отклонение 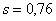 . Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения
. Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения  (генерального стандартного отклонения) с надёжностью
(генерального стандартного отклонения) с надёжностью  .
.
Решение: Доверительный интервал для оценки неизвестной дисперсии нормально распределённой генеральной совокупности определяется следующим образом:
нормально распределённой генеральной совокупности определяется следующим образом:
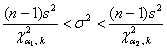 , где
, где 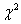 – распределение «хи-квадрат», а
– распределение «хи-квадрат», а 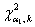 ,
, 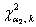 – его критические значения, вычисленные для
– его критические значения, вычисленные для 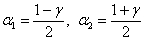 ,
, 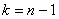
Данный интервал с вероятностью (надёжностью) накрывает истинное значение
(надёжностью) накрывает истинное значение  . И если из всех частей неравенства извлечь корни, то получим соответствующий интервал для оценки генерального стандартного отклонения:
. И если из всех частей неравенства извлечь корни, то получим соответствующий интервал для оценки генерального стандартного отклонения:
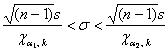
Значения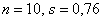 известны, и вычислим:
известны, и вычислим:
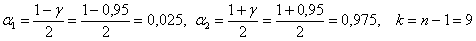
и теперь, по таблице критических значений распределения находим:
находим:
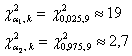
Получены различные значения, и наш доверительный интервал будет асимметричным (ввиду асимметрии распределения «хи-квадрат»):
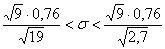 – не забываем извлечь корни из знаменателей!
– не забываем извлечь корни из знаменателей!
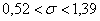 – таким образом, с вероятностью
– таким образом, с вероятностью  можно утверждать, что данный интервал накроет генеральное стандартное отклонение
можно утверждать, что данный интервал накроет генеральное стандартное отклонение  .
.
Ответ: 1)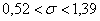 , 2)
, 2) 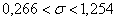 .
.
Пример 4
В результате обработки экспериментальных данных объёма мы получили следующие выборочные характеристики:
мы получили следующие выборочные характеристики: 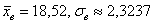 .
.
В предположении о нормальном распределении генеральной совокупности, с надёжностью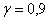 определить доверительные интервалы:
определить доверительные интервалы:
1) для оценки неизвестной генеральной средней ;
;
2) для оценки генерального среднего квадратического отклонения двумя способами – с помощью распределения хи-квадрат:
двумя способами – с помощью распределения хи-квадрат:
 и приближённо, по формуле
и приближённо, по формуле 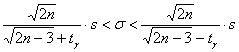 , где
, где  .
.
И заметьте, что здесь «плакал» лёгкий способ построения интервала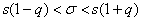 , так как в стандартной таблице отсутствуют значения для
, так как в стандартной таблице отсутствуют значения для  .
.
Решение: вычислим исправленное среднеквадратическое отклонение:
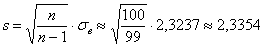
1) Определим доверительный интервал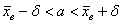 , где
, где 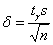 .
.
Для уровня доверительной вероятности и объёма выборки
и объёма выборки  по соответствующей таблице найдём
по соответствующей таблице найдём 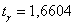 .
.
Вычислим точность оценки:
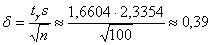
Таким образом:
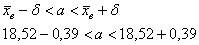
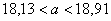 – с вероятностью
– с вероятностью  данный интервал накроет генеральное среднее значение
данный интервал накроет генеральное среднее значение  .
.
2) Найдём доверительный интервал для генерального стандартного отклонения .
.
а) С помощью распределения
:

Вычислим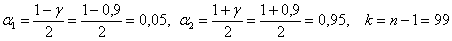 и с помощью соответствующей функции Экселя найдём:
и с помощью соответствующей функции Экселя найдём:
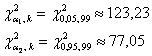
Таким образом:
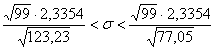
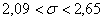 – искомый интервал, накрывающий генеральное значение
– искомый интервал, накрывающий генеральное значение  с вероятностью
с вероятностью  .
.
б) Дадим интервальную оценку приближенно, с помощью формулы:

Коэффициент доверия найдём из соотношения . В данном случае:
. В данном случае:
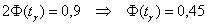 , и с помощью таблицы , выясняем, что
, и с помощью таблицы , выясняем, что 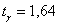 .
.
Таким образом:
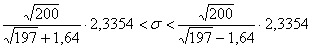
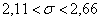 – искомый интервал.
– искомый интервал.
Ответ:
1) ,
,
2)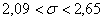 с помощью распределения
с помощью распределения  и
и 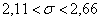 приближённо.
приближённо.
Задание на дом.
По результатам выборочного исследования
 объектов найдена выборочная средняя
объектов найдена выборочная средняя 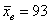 .
.
1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения менее чем на 3, если известно, что генеральная совокупность распределения нормально с дисперсией 400?
2) Определить доверительный интервал, который с надежностью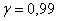 накроет истинное значение генеральной средней.
накроет истинное значение генеральной средней.
Ответ:
Пример 3
По
Решение: Доверительный интервал для оценки неизвестной дисперсии
Данный интервал с вероятностью
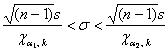
Значения
и теперь, по таблице критических значений распределения
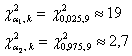
Получены различные значения, и наш доверительный интервал будет асимметричным (ввиду асимметрии распределения «хи-квадрат»):
Ответ: 1)
Пример 4
В результате обработки экспериментальных данных объёма
В предположении о нормальном распределении генеральной совокупности, с надёжностью
1) для оценки неизвестной генеральной средней
2) для оценки генерального среднего квадратического отклонения
 и приближённо, по формуле
и приближённо, по формуле 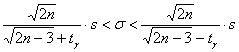 , где
, где И заметьте, что здесь «плакал» лёгкий способ построения интервала
Решение: вычислим исправленное среднеквадратическое отклонение:
1) Определим доверительный интервал
Для уровня доверительной вероятности
Вычислим точность оценки:
Таким образом:
2) Найдём доверительный интервал для генерального стандартного отклонения
а) С помощью распределения
:

Вычислим
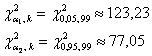
Таким образом:
б) Дадим интервальную оценку приближенно, с помощью формулы:

Коэффициент доверия найдём из соотношения
Таким образом:
Ответ:
1)
2)
Задание на дом.
По результатам выборочного исследования
1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения менее чем на 3, если известно, что генеральная совокупность распределения нормально с дисперсией 400?
2) Определить доверительный интервал, который с надежностью