Файл: Учебнометодическое пособие по экономической теории Микроэкономика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 151
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕСИОНАЛЬНОГО ОБРАЗОВАНИЯ
КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Экономическая теория
(микроэкономика)
Учебно – методическое пособие
Кемерово 2007
Учебно-методическое пособие по экономической теории «Микроэкономика» / составители: д. э. н., профессор Зобова Л. Л., к. э. н., доцент Евдокимова Е. К., к. э. н., доцент Щербакова Л. Н.
Учебно-методическое пособие разработано по курсу Экономическая теория (микроэкономика) для специальностей «Экономика и управление на предприятии», «Маркетинг», «Финансы и кредит», «Налоги и налогообложение» в соответствии с требованиями ГОС ВПО и содержит разные по форме задачи и упражнения с решением, теоретическим обоснованием, словарь основных понятий микроэкономики.
Утверждено
методической комиссией
экономического факультета
Протокол № 7
« 3 » мая 2007 г.
Председатель метод. комиссии
Козлова О. Н. ____________
Утверждено
на заседании кафедры
«Экономическая теория»
Протокол № 13
« 20 » апреля 2007 г.
Зав. кафедрой, профессор
Шабашев В. А. ____________
Содержание
Введение
-
Теория потребительского рынка. -
Спрос и предложение. Рыночное равновесие. Эластичность спроса и предложения. -
Рынки факторов производства. -
Производственная деятельность фирмы. Поведение фирмы в условиях совершенной и несовершенной конкуренции.
Словарь микроэкономических понятий
Введение.
Появление нового наполнения курса экономической теории обусловило необходимость новых навыков у студентов. Экономика включает в себя огромное количество графиков, формул, объяснение тех или иных закономерностей развития экономики чаще всего заменяется математическим иллюстративным материалом. В литературе данного периода нарастает число сборников задач и упражнений, практикумов, однако объяснение задач зачастую осуществляется очень скупо, либо вообще ограничивается одними ответами.
В предлагаемом вам методическом пособии ставятся следующие цели:
1. В качестве объекта исследования взять 4 наиболее объемные и наполненные математическими приемами темы.
2. Максимально подробно рассмотреть решение задач.
3. Научить студентов работать с различными творческими заданиями: тестами, «верно – неверно», вставить пропущенное слово.
4. При объяснении задач ставится цель научить студентов обращать внимание на теоретический аспект в решении задач, а не только осуществлять сам счет.
Теория потребительского поведения.
Основные термины и понятия
Полезность и ценность, величина ценности, эффект дохода, меновая и потребительная ценность, эффект замещения, закон убывающей предельной полезности, полезность, правило максимизации полезности, функция полезность, кривая совокупной полезности, кривая предельной полезности, кривая безразличия, предельная норма замещения, карта безразличия, положение равновесия, потребительский излишек, кривая цена – потребление, кривые Энгеля, законы Госсена, предпочтение, транзитивное предпочтение, принцип равной полезности, угловое равновесие.
Задания тестового характера помогают обратить внимание на те нюансы, которые чаще всего упускаются из виду при общем изучении темы. Рассмотрим разные примеры тестовых заданий.
1. Закон убывающей предельной полезности означает, что:
а) отношение предельных полезностей к ценам на предметы роскоши меньше чем на товары первой необходимости;
б) полезность, приносимая каждой последующей единицей товара, убывает по мере увеличения количества приобретаемых товаров;
в) отношение предельных полезностей к ценам одинаково для всех товаров;
г) полезность приобретаемых товаров убывает по мере увеличения дохода потребителя;
д) ни один из ответов не является верным.
Верен второй ответ. Это задание на закрепление знаний. Для его выполнения нужно точно знать и понимать данный закон.
2. Какое из следующих утверждений является неверным?
а) каждая точка на кривой безразличия означает комбинацию двух товаров;
б) каждая точка на бюджетной линии означает комбинацию двух товаров;
в) все точки на кривой безразличия означают одинаковый уровень полезности;
г) все точки на бюджетной линии означают одинаковый уровень полезности;
д) наклон кривой безразличия характеризует норму, в соответствии с которой одно благо может быть замещено другим благом без изменения уровня полезности для потребителя.
В данном случае нужно выбрать неправильный ответ. В таком случае все остальные ответы правильны. Следовательно, студент может идти двумя путями либо он точно знает, что такое кривая безразличия и бюджетная линия тогда он быстро находит один неправильный ответ (г). Но возможна другая ситуация. Если студент сомневается или имеет не полные знания, то он попробует пойти путем исключения. Ответы «а», «б», «в», – правильны, поэтому «г» – искомое утверждение.
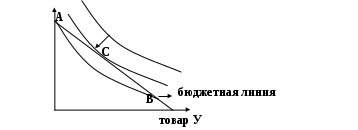
3. Если потребитель выбирает комбинацию, представленную точкой, лежащей на плоскости, ограниченной бюджетной линией, то он:
а) максимизирует полезность;
б) желает купить больше товаров, чем позволяет его бюджет;
в) не полностью использует свой бюджет;
г) находится в положении потребительского равновесия;
д) ни один из ответов не является верным.
В данном задании необходимо воспользоваться умением графических построений. Построим данную комбинацию
По графику мы видим, что точка (С) лежит левее бюджетной линии, по сути дела, находится на другой бюджетной линии, соответствующей меньшему доходу. Поэтому выбираем ответ (в)

4а. Какой из следующих перечней предельной полезности иллюстрирует закон убывающей предельной полезности?
а) 200, 150, 100, 50;
б) 200, 300, 400, 500;
в) 200, 200, 200, 200;
г) 200, 250, 270, 280;
д) 200, 150, 150, 150;
4б. Какой из следующих перечней значений общей полезности иллюстрирует закон убывающей предельной полезности?
а) 200, 300, 400, 500;
б) 200, 450, 750, 1100;
в) 200, 400, 1600, 9600;
г) 200, 250, 270, 280;
д) 200, 350, 450, 600.
Эти задания являются примером тех ситуаций, когда ответ необходимо искать на основе расчетов при знании определенных категорий, в данном случае, предельной и общей полезности, закона убывающей предельной полезности.
Сначала мы рассмотрим тест 4а, так как именно в нем даны задания с предельной полезностью. В случае б) она растет, в случае в) она становится неизменной, в случае г) она растет неравным темпом в отличие от б), в случае д) предельная полезность после разового падения стала неизменной, поэтому верен ответ а), где предельная полезность падает равным темпом.
В случае с заданием 4б, необходимо сначала вести расчеты, а потом искать данные, соответствующие этому закону.
МИn+1=ТИn+1 –ТИn
а) ТИ: 200, 300, 400, 500; МИ: 100, 100, 100;
б) ТИ: 200, 450, 750, 1100; МИ: 250, 300, 350;
в) ТИ: 200, 400, 1600, 9600; МИ: 200, 1200, 8000;
г) ТИ: 200, 250, 270, 280; МИ: 50, 20, 10;
д) ТИ 200, 350, 450, 600. МИ: 150, 100, 150.
Мы рассчитывали предельную полезность, вычитая рядом стоящие цифры, например, в случае а) (300-200); (400-300); (500-400), затем получили ряды предельных полезностей. Убывание, причем постоянное, наличествует в случае г)
Теперь обратимся к решению задач.
Задача №1.
Определить предельную полезность по следующим данным об общей полезности. Общая полезность пяти съеденных порций мороженого равна 14 единицам, шести – 15 единицам, а семи – 10.
Решение. В данной задаче предельная полезность определяется по формуле:
МИn+1=ТИn+1 –ТИn
Условия задачи подсказывают, что предельную полезность можно определить только для шестого и седьмого мороженого:
МИ6=ТИ6-ТИ5=15-14=1
МИ7=ТИ7-ТИ6=10-15=-5
Задача №2.
Маржинальная полезность первого съеденного апельсина равна 5 единицам, второго – 3 единицам, а третьего – 2. Вычислите общую полезность.
Решение. В данной задаче важно знать и понимать два момента. Во-первых, это математическое выражение сути предельной полезности, то есть
МИn+1=ТИn+1 –ТИn
Во-вторых, в задаче дана маржинальная полезность первого товара. Находим её по формуле:
МИ1=ТИ1-ТИ0, получаем, что МИ1=ТИ1
Получаем важный для данной задачи момент: предельная полезность первой единицы равна общей полезности, получаемой при потреблении одной единицы товара.
Теперь решение задачи становится понятным. Общую полезность находим из формулы предельной полезности.
МИn+1=ТИn+1 –ТИn, то есть общая полезность для любой единицы товара будет определяться как общая полезность, полученная для предыдущих единиц плюс добавочная (предельная) полезность, полученная от потребления данной единицы.
ТИ1=МИ1=5 ед.
ТИ2=ТИ1+МИ2=5 ед.+3 ед.=8 ед.
ТИ3=ТИ2+МИ3=8 ед.+2 ед.=10 ед.
Данную задачу можно рассмотреть несколько иным способом. ТИ1=МИ1, тогда ТИ2=МИ1+МИ2, тогда
Задача №3.
Заполните пропуски в таблице.
| Количество товара | Общая полезность | Предельная полезность |
| 1 | | 10 |
| 2 | 18 | |
| 3 | 25 | |
Решение. Данная задача решается, когда студент уже освоил способ расчета и предельной, и общей полезности, однако ему необходимо научиться выбирать, какую из известных ему формул, познанных способов расчета употребить в первую очередь, как в случае с данной таблицей. В первую очередь, студенту надо вспомнить, что МИ1=ТИ1, тогда заполняется первая строка в колонке 2 (общая полезность). ТИ1=10=МИ1. Теперь вторая колонка дает всю информацию об общей полезности. Следовательно МИ2, МИ3 можно определять по известной формуле расчета предельной полезности. Заполненная таблица имеет вид:
| Количество товара | Общая полезность | Предельная полезность |
| 1 | (10) | 10 |
| 2 | 18 | (8) |
| 3 | 25 | (7) |
По аналогии заполняется следующая таблица:
| Количество товара | Общая полезность | Предельная полезность |
| 1 | 51 | (51) |
| 2 | (91) | 40 |
| 3 | 125 | (34) |
Как и в предыдущей задаче решение начинается с того, что МИ1=ТИ1, это дает возможность посчитать общую полезность второй единицы ТИ2=МИ1+МИ2=51+40=91. После этого можно найти МИ3=ТИ3-ТИ2=125-91=34.
Задача №4.
Первое яблоко доставляет Ивану удовлетворение, равное 8. Каждое следующее яблоко доставляет добавочное удовлетворение, на 2 меньше предыдущего. Начиная с какого яблока суммарное удовлетворение от потребления яблок будет уменьшаться?
Решение. В данной задаче необходимо понимать теоретическое различие совокупной полезности и предельной полезности, их математическое значение, а также различие графиков общей полезности и предельной полезности.
Известно, что общая полезность с увеличением количества благ постепенно возрастает, предельная полезность каждой дополнительной единицы блага неуклонно уменьшается. Максимум удовлетворения общей полезности достигается в точке А, когда предельная полезность становится равно 0 (рис.1). Это означает, что благо полностью удовлетворяет потребность.
Если дальнейшее потребление приносит вред (предельная полезность блага отрицательна), то общая полезность снижается (см. отрезок АВ, рис.1).
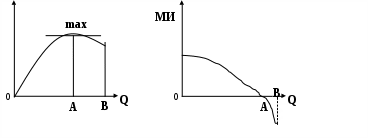
ТИ
рис.1
МИn+1 = МИn-2 МИ3 = 4 ТИ3 = 18
МИ1 = 8 ТИ1 = 8 МИ4 = 2 ТИ4 = 20
МИ2 = 6 ТИ2 = 14 МИ5 = 0 ТИ5 = 20
Из всего вышесказанного следует, что в данной задаче нам надо искать такое яблоко, предельная полезность которого будет равна 0. Можно рассчитать по обычной формуле предельной полезности и получить, что
МИ1=8 – по условию задачи.
(МИn+1=МИn-2) – такой вид примет формула зависимости предельной полезности последующих единиц яблока. Тогда
МИ2=6, МИ3=4, МИ4=2, МИ5=0.
Получается, что пятое яблоко дает максимальную суммарную полезность, а с шестого она начинает убывать. В то же время
эту задачу можно решить по формуле арифметической прогрессии, которая будет иметь вид МИi=10-2i.
Составляем уравнение: 10-2i,<0
i>5,
то есть с шестого яблока полезность уменьшается.
Следующее задан е будет посвящено проблеме потребительского равновесия, суть которого заключается в выборе потребителем такого набора товаров, который будет нести максимальную общую полезность, возможную при данном доходе. При этом информацию о полезности будет нести кривая безразличия, а информацию о доходе – бюджетная линия.
Задача №5.
Докажите, что кривые безразличия одного рационального потребителя друг с другом не пересекаются.
Доказательство.Предположим обратное, т.е. что две кривые безразличия, соответствующие разным уровням полезности, пересекаются. Тогда точка пересечения характеризуется двумя значениями полезности. Чего быть не может. Поэтому две кривые безразличия, соответствующие разным уровням полезности, не могут пересекаться.
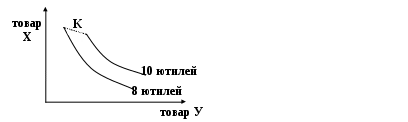
К – предполагаемая точка пересечения.
Задача №6.
Докажите, что оптимум потребителя в точках А и В не достигается.
Доказательство:Бюджет, которым располагает потребитель, достаточен для достижения полезности и выше, чем обладает потребитель на рисунке кривой безразличия. Для достижения того же уровня полезности достаточно уровня дохода меньшего, нежели указывает бюджетная линия, так как можно провести бюджетную линию с меньшим уровнем дохода и пересекающую указанную кривую безразличия. Таким образом, точки А и В не соответствую оптимуму потребителя. В точке С полезность больше, чем по краям: в точках А и В.

Задача № 7.
На рисунке изображена линия движения
точки оптимума некоторого российского потребителя с ростом доходов при выборе между яблоками и апельсинами. Объясните это явление.
Н
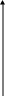
Апельсины, кг
аправление кривой показывает изменение предпочт
Яблоки, кг
ений некоторого потребителя с ростом его дохода.






Яблоки, кг
Объяснение.При увеличении дохода сверх какого-то предела объем потребления яблок начинает сокращаться. Яблоки вытесняются апельсинами. Экономисты говорят, что яблоки служат для нашего потребителя товаром низшего порядка по сравнению с апельсинами. Бюджетные линии ,изображенные на графике, показывают рост дохода, который вызывает эффект замещения яблок апельсинами.
Задача №8.
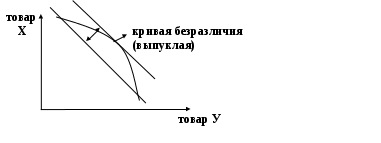
Покажите, что кривая безразличия невыпукла, т.е. что она вогнута или, в крайнем случае, линейна.
Доказательство.Предположим противное, т.е. что кривая безразличия выпукла. Проведем бюджетную линию так, что она касается этой кривой безразличия. Увеличивая бюджет, мы не можем достичь того же уровня полезности, а уменьшая – можем даже в двух точках. Этого не может быть. Поэтому кривая безразличия невыпукла.
Задача №9.
Доказать, что наилучшее использование суммы D достигается в точке касания соответствующего бюджетного ограничения и некоторой кривой безразличия.
Доказательство.В этой задаче показано, что при пересечении в двух точках кривой безразличия оптимума не достигается. Поэтому оптимум может достигаться только в точке касания бюджетного ограничения и кривой безразличия. Такая точка касания существует, поскольку кривая безразличия вогнута.
Другое доказательство таково. Проведем некоторую кривую безразличия, лежащую выше нашей бюджетной линии. Будем снижать уровень полезности до тех пор, пока соответствующая кривая безразличия не коснется нашей бюджетной линии. Это и будет оптимум потребителя.
товар Х
Задача №10.
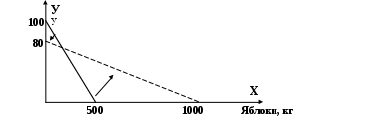
Построить линию бюджетного ограничения для яблок и мяса при доходе потребителя, равном 100 динаров в месяц с учетом цен: яблоки – 2 динара за 1 кг, а мясо – 10 динаров. Как сместится линия при снижении цены яблок до 1 динара и при росте цены мяса на 25%? Выписать уравнения обеих бюджетных прямых.
Решение.На 1000 динаров можно купить 1000/2=500 кг яблок или 1000/10=100 кг мяса. Соединив точки (500, 0) и (0, 100), получим бюджетное ограничение.
Была линия, заданная уравнением
Y=100-0,2 xX? где Х, У – количества яблок и мяса. Стала бюджетная линия ,заданная уравнением У=80-0,08 х Х, так как 1000/1=1000 кг яблок и 1000/(1,25 х 10)=80 кг мяса.
Мясо, кг
В данной задаче имеет значение тот факт, что бюджетная линия графически изображается прямой линией, поэтому для её построения достаточно найти две точки, лежащие на координатных осях. В первом случае мы предположили, что продаются только яблоки, получили ответ 500 кг; во втором случае – только мясо, получили 100 кг мяса.
Уравнение бюджетной линии мы строим, исходя из формулы I=PxX+PyУ, где I – доход потребителя,
Px и X – цена и количество одного товара, Py и Y – цена и количество второго товара. Из вышеуказанного уравнения выделим У.
Следовательно в нашей задаче 0,2 =
Задача №11.
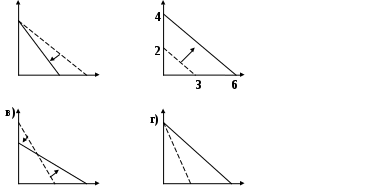
Как изменились цены, если прямая бюджетного ограничения сдвинулась таким образом, как это изображено на рисунке?
а)
б)
а) Цена одного товара увеличилась.
б) Цены обоих товаров снизились в два раза.
в) Цена одного товара выросла, а другого снизилась.
г) Цена одного товара снизилась.
Решение. В данной задаче важно понимать, что снижение цен ведёт к росту покупательной способности того же дохода, а рост цен – к снижению его покупательной способности, поэтому в первом случае бюджетная линия смещается вправо и вверх, во втором случае – влево и вниз. Если цена меняется только на один товар, то смещается только соответствующая часть бюджетной линии.
Далее мы рассмотрим задачи на построение кривых безразличия для различных благ. В случае со взаимодополняемыми благами существует 2 варианта. Взаимодополняемость бывает жесткой, абсолютной, когда одному благу соответствует определенное количество другого блага, например, лыжи и крепления к ним, относительной, например, чай и сахар, автомобиль и бензин. Для абсолютно взаимозаменяемых благ предельная норма замещения равна нулю:
Взаимозаменяемость тоже бывает совершенной, когда одно благо может полностью заменить другое, например, красные и розовые гвоздики, а может быть относительной, например, чай и кофе ,сливочное масло и маргарин. Графически совершенная взаимозаменяемость изображается параллельными кривыми безразличия. Предельная норма замещения в этом случае постоянна:
Задача №12.
Кто из девочек, скорей всего, отличница, если их кривые безразличия таковы:
К

Решение. Варвара не любит танцевать и предпочитает делать уроки. Ксения – наоборот. Поэтому более вероятно, что Варвара является отличницей.
Задача №13.
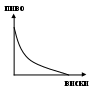
Что можно сказать о взаимозаменяемости и взаимодополняемости этих товаров для Джона?
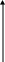
хлеб
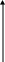

мясо


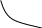

масло
рыба
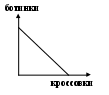
Решение. Обратите внимание на то, что частично взаимозаменяемые пары продуктов пиво – виски и рыба – мясо по-разному ценны для Джона. Видимо, он пьет весьма умеренно. Но ест много: при относительном недостатке мяса он может съесть очень много рыбы, и наоборот. Джону все равно – носить ли ботинки или кроссовки. Это определяется только отношением их цен. Джон ест только хлеб с маслом. Один хлеб или масло сверх того, что можно намазать на бутерброд, для него ценности не представляют.
Задача№14.
О
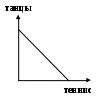
конфеты
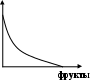 пишите вкусы Людмилы по известным кривым безразличия:
пишите вкусы Людмилы по известным кривым безразличия: 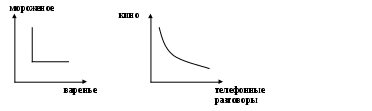
Решение. Танцы и теннис абсолютно взаимозаменяемы и любимы. Кино и телефонные разговоры взаимозаменяемы и дополняют друг друга, точно так же как и фрукты, и конфеты. Обратите внимание на то, что кривая безразличия конфет и фруктов касается осей. Это означает, что при увеличении потребления одного из продуктов сверх количества, соответствующего точке касания ,увеличения полезности не происходит. Поэтому для Людмилы наступает насыщение конфет и фруктов. А вот мороженое она предпочитает дополнять вареньем, и наоборот. Эти продукты для Людмилы являются абсолютно взаимодополняемыми.
Для закрепления материала выполним задание «верно-неверно» и вставить пропущенное слово.
-
Кардиналистский подход отрицает измеримость полезности (неверно). -
Кардиналистский подход не допускает суммирования полезностей потребителей (неверно). -
Полезность измеряется в единицах продукта (неверно). -
Полезность может быть отрицательной (неверно). -
Предельная полезность не убывает (неверно). -
Кривые безразличия не пересекаются (верно). -
Бюджетная линия – это изображение наборов, имеющих равную стоимость (неверно). -
Равновесный набор находится на бюджетной линии (верно). -
При равновесии потребителя цена каждого товара равна соответствующему значению предельной полезности (верно).
-
Полезность зависит от объемов потребляемых продуктов. -
Экономическая школа, широко использующая понятие предела, называется маржинализм. -
Прирост полезности, вызванный увеличением объема потребления продукта на единицу, называется предельной полезностью. -
Полезность называется также совокупной полезностью.
Спрос и предложение. Рыночное равновесие. Эластичность спроса и предложения.
Основные термины и понятия
Спрос, объем спроса, кривая спроса, сдвиг кривой спроса, предложение, объем предложения, кривая предложения, сдвиг кривой предложения, равновесный объем, равновесная цена, дефицит, излишек, товары – субституты, комплементарные товары, нормальные товары, низшие товары, цена продавца, цена покупателя.
Эластичность, точечная эластичность, дуговая эластичность, ценовая эластичность спроса, гибкий (эластичный) спрос, жесткий (неэластичный) спрос, спрос с нулевой эластичностью, спрос с бесконечной эластичностью, спрос с единичной эластичностью, факторы ценовой эластичности спроса, перекрестная ценовая эластичность, эластичность взаимозаменяемых товаров, эластичность взаимодополняемых товаров, эластичность спроса по доходу, товары первой необходимости, предметы роскоши, эластичность предложения, факторы эластичности предложения, выручка при жестком спросе, выручка при гибком спросе.