ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 53
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Блочное прогр.doc
Блочное программирование
Итак, мы достаточно подробно изучили симплекс-метод, двойственный симплекс-метод, а также модифицированный симплекс-метод.
Что можно сказать об этих методах? Прежде всего, это - универсальные, конечные методы.
Конечность - это гарантия решения задачи ЛП за конечное количество шагов (пусть и очень большое).
Универсальность. Это означает, что данные методы практически не учитывают особенности строения матрицы коэффициентов ограничений. Главное, что задача относится к классу задач ЛП:
<c,x> max ,
AX=A0 ,
x 0 .
И вот здесь мы сталкиваемся с фундаментальным "законом" математического программирования: за универсальность нужно платить. Иными словами, конкретную задачу лучше, эффективнее решать методом, ориентированным на особенности именно этой задачи, чем методом, полностью игнорирующим любые особенности.
Например, в нелинейном программировании вообще нет универсальных методов. Практически каждый метод (за исключением, разве что, полного перебора) предъявляет определенные требования, как к целевой функции, так и к функциям, определяющим множество допустимых решений1.
Но вернемся к линейному программированию.
Многие классы широко распространенных задач ЛП обладают специфическим строением матрицы ограничений (A) . Эти особенности позволяют существенно снизить трудоемкость решения данных задач.
Первый из рассматриваемых нами классов представляют задачи так называемого "блочного программирования".
Задачи блочного программирования
Некоторые задачи ЛП большой размерности имеют такие структурные особенности, которые позволяют найти их оптимальное решение путем т.н. декомпозиции (или разложения) исходной задачи на ряд подзадач меньшей размерности. Причем эти подзадачи решаются практически независимо друг от друга. Основной эффект при таком подходе связан с тем, что существенно легче решить много "маленьких" задач, чем одну, но "большую". В математическом программировании это связано с полиномиальной и, даже, экспоненциальной зависимостью трудоемкости решения задач от их размерности.
Преимущество методов, использующих "декомпозицию" исходной задачи на подзадачи меньшей размерности заключается в том, что с помощью этих методов оказывается возможным решение задач такой размерности, которые не удается решить другими методами из-за практически невыполнимого объема вычислений.
Ситуации, приводящие к постановке подобных задач, встречаются довольно часто.
Например, это - задачи планирования производственной деятельности предприятий, входящих в объединение. Хотя каждое из таких предприятий может иметь свои независимые ограничения, производственные программы отдельных предприятий обычно согласовывают на верхнем уровне управления из-за объективно существующих ограничений (связанных, например, с общим объемом финансовых ресурсов, которыми располагает объединение).
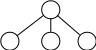
При этом возникает задача ЛП, обладающая структурой, которую в схематичной форме можно представить следующим образом.
| Целевая функция | | extr | |||||
| | | | | | | | |
| Общие ограничения | | | |||||
Независимые ограничения
| п/п 1 | | | | | | | |
| | | | | | | | |
| | п/п 2 | | | | | | |
| | | | | | | | |
| | | | | | п/п L | | |
Что здесь интересно? Независимые ограничения имеют блочно-диагональную структуру. При отсутствии общих ограничений различные виды производств могут рассматриваться, как совершенно независимые.
Поэтому нет проблем, если общие ограничения, образующие т.н. БЛОК-СВЯЗКУ, отсутствуют:
| Целевая функция | | extr |
Независимые ограничения
| п/п 1 | | | | | | | |
| | | | | | | | |
| | п/п 2 | | | | | | |
| | | | | | | | |
| | | | | | п/п L | | |
Решить подобную задачу - это просто "разрезать" ее на L независимых задач, решить каждую из этих задач и объединить полученные оптимальные решения.
При этом:
Наличие же блока-связки, в общем случае, приводит к тому, что
Теория блочного программирования ориентирована на решение методом декомпозиции задач, имеющих как общие, так и независимые ограничения.
Класс задач с подобной структурой достаточно широк. В частности, к этому классу очень просто сводятся задачи, имеющие матрицу ограничений вида:
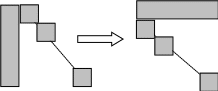
Ясно, что двойственная задача имеет блочно-диагональную структуру с блоком-связкой.
Более того, при сильной разреженности матрицы ограничений можно (небезуспешно) попытаться путем перестановки строк и столбцов придать произвольной задаче подобную структуру.
Метод декомпозиции Данцига-Вулфа: построение координирующей задачи
Рассмотрим некоторую задачу ЛП, имеющую блочно-диагональную структуру.
Пусть задача имеет n переменных, пронумерованных числами натурального ряда: {1,2,...,n}.
Множество индексов (номеров) переменных разобьем на L подмножеств по принципу принадлежности соответствующих переменных к 1-му, 2-му, ... , L-му диагональному блоку.
1={1, 2, ... ,q1},
2={ q1+1, q1+2, ... ,q2},
................................
={ q - 1+1, q - 1+2, ... ,q},
................................
L={ qL - 1+1, qL - 1+2, ... ,qL}.
Здесь qL=n , q0=0.
Такое разбиение позволяет записать задачу с блочно-диагональной структурой в следующем виде.
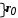 ,
,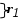 ,
,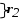 =
=.
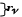 ...........................................................................................
............................................................................................
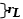 ...........................................................................................
...........................................................................................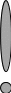
Здесь:
Aj-
-мерный вектор-столбец коэффициентов при переменной xj из блока-связки;
Dj - вектор-столбец коэффициентов при переменной xj , принадлежащий диагональному блоку (если j ). Его размерность -
Размерность этой задачи
А теперь, запомнив формальную запись этой задачи, приступим к изложению общей идеи метода декомпозиции Данцига-Вулфа.
Будем считать, что в задаче имеется один блок-связка AX=B0 и один-единственный диагональный блок DX=B*.
Здесь B*=
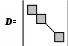
Теперь задачу можно записать следующим образом:
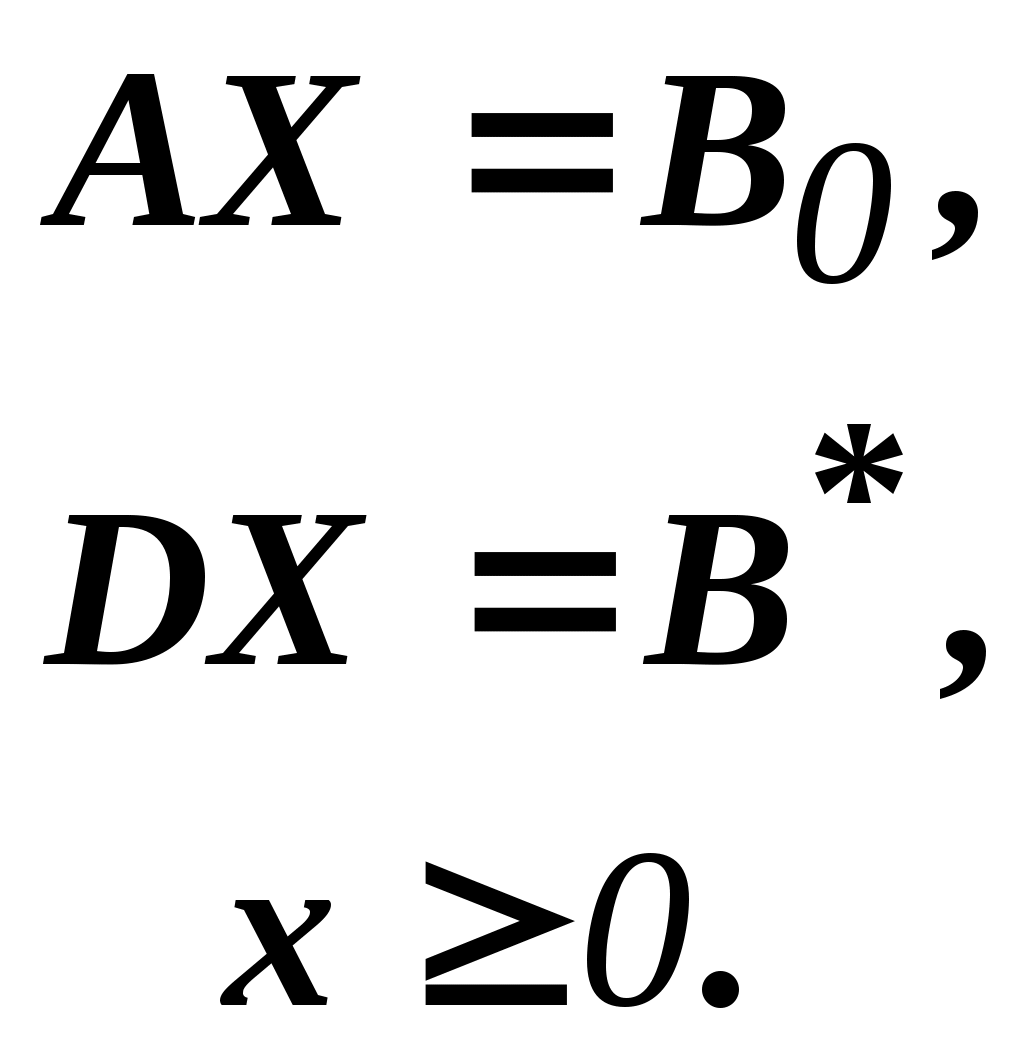
Казалось бы, здесь потеряна специфика блочно-диагональной структуры задачи. Позже будет показано, что это не так.
Будем, для простоты, считать, что
Как известно, любую точку ограниченного выпуклого множества можно представить, как выпуклую линейную комбинацию экстремальных точек (вершин).
То есть, если