ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 60
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- координаты вершин множества  , то это множество состоит из всех возможных точек вида:
, то это множество состоит из всех возможных точек вида:
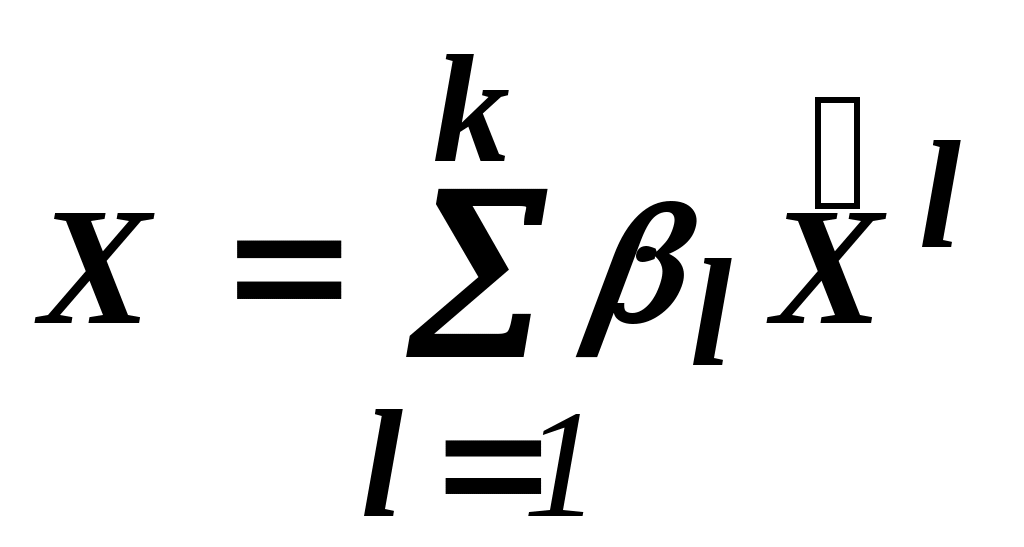 , где
, где 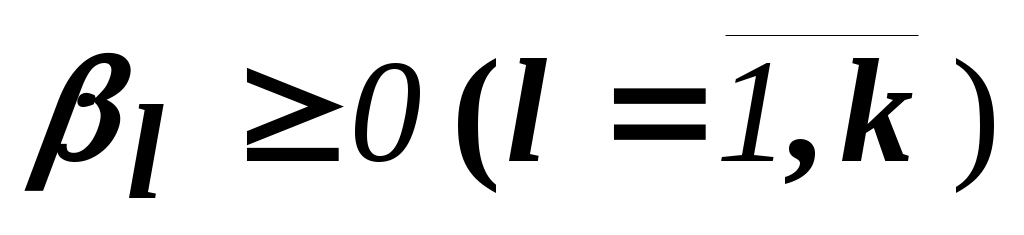 и
и 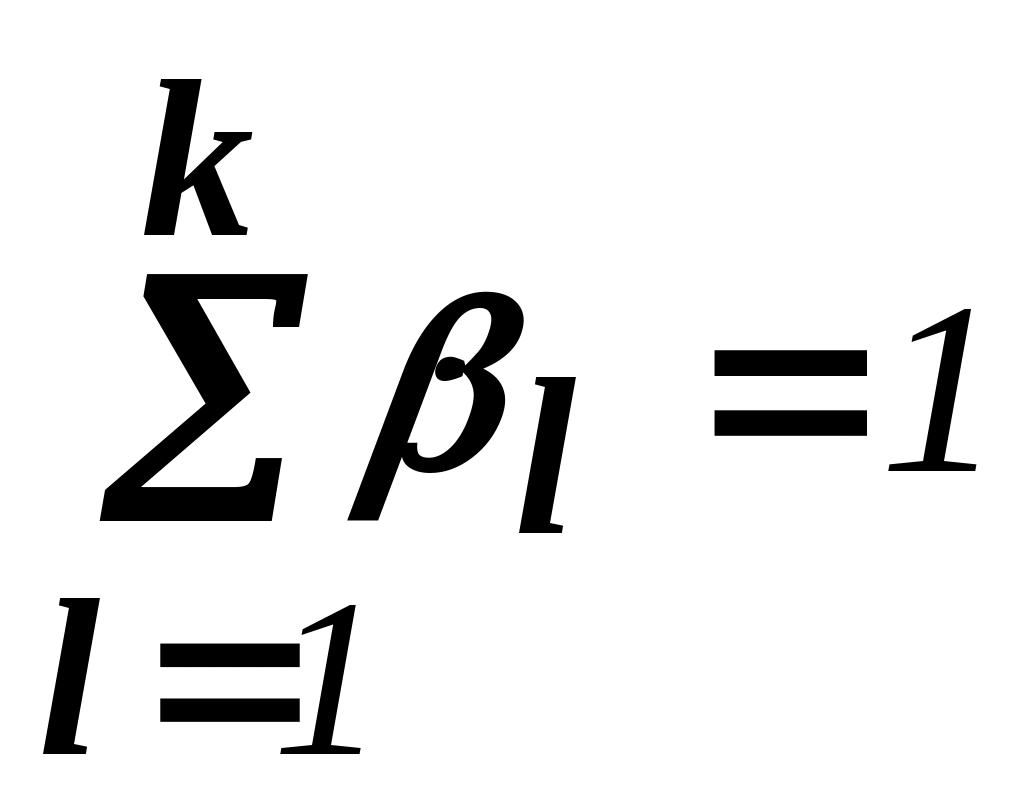 . ()
. ()
Очевидно, что любая точка, представленная в виде (), удовлетворяет всем ограничениям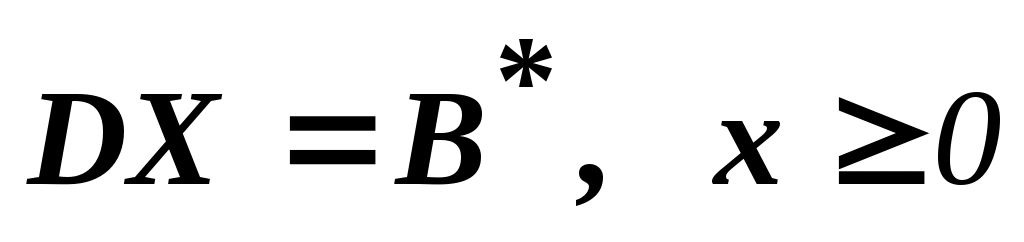 .
.
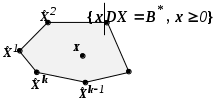
Здесь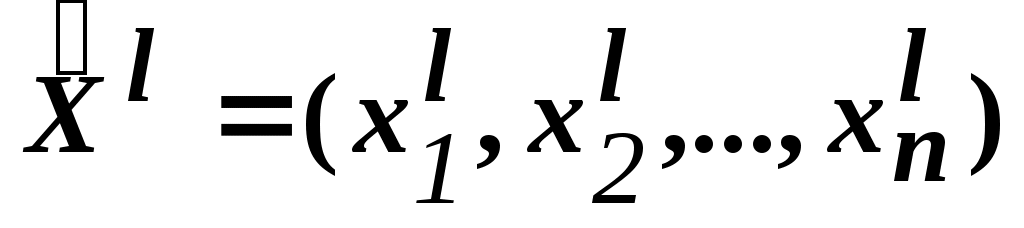 .
.
Это обстоятельство позволяет видоизменить исходную задачу таким образом, что из рассмотрения будут исключены все ограничения диагонального блока.
Примем обозначения:
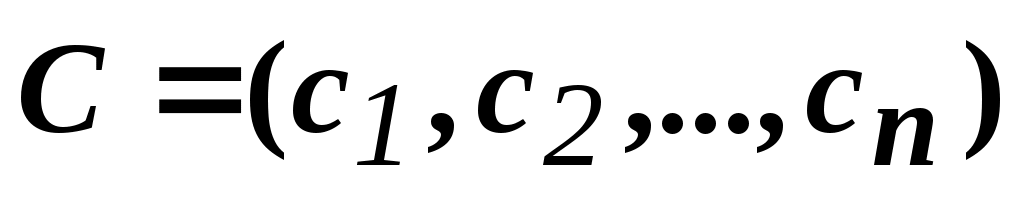 - вектор коэффициентов ЦФ;
- вектор коэффициентов ЦФ;
А=(А1,А2, ... ,Аn) - матрица, составленная из векторов блока-связки.
Теперь задача приобретает следующий вид:
()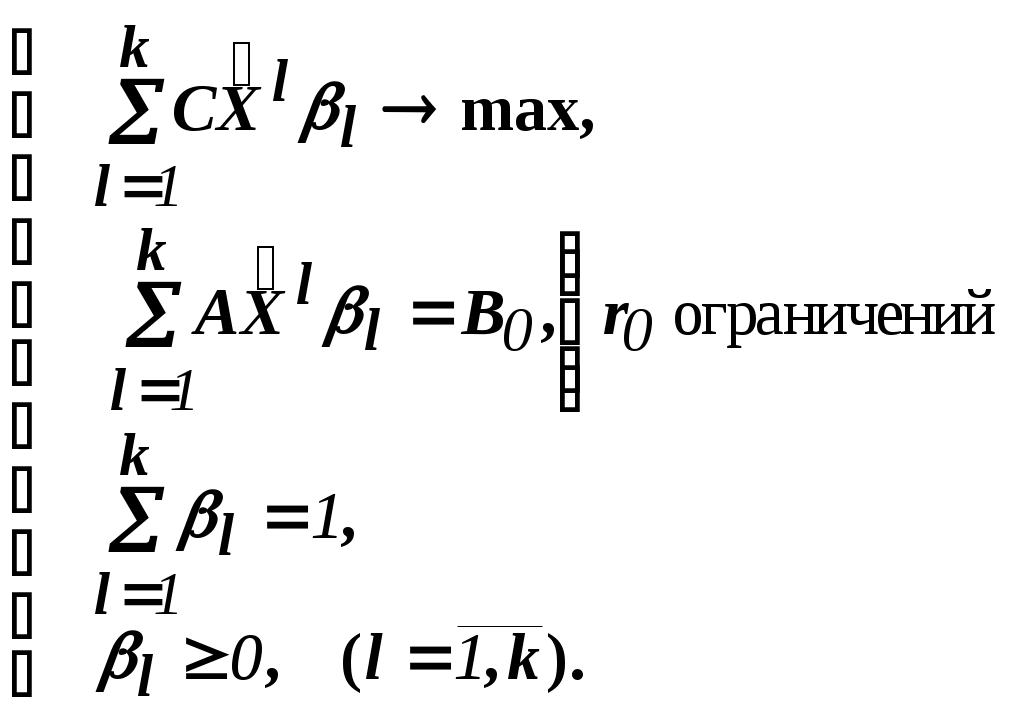

Как видно, все ограничения, составляющие диагональный блок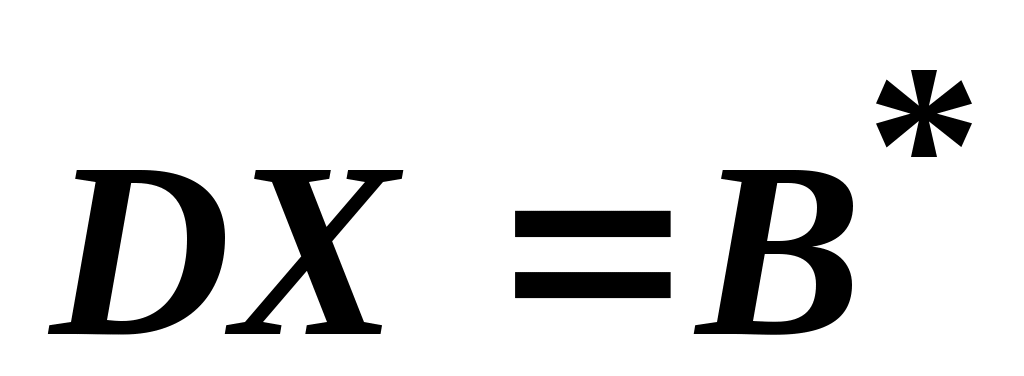 , "исчезли". А таких ограничений
, "исчезли". А таких ограничений 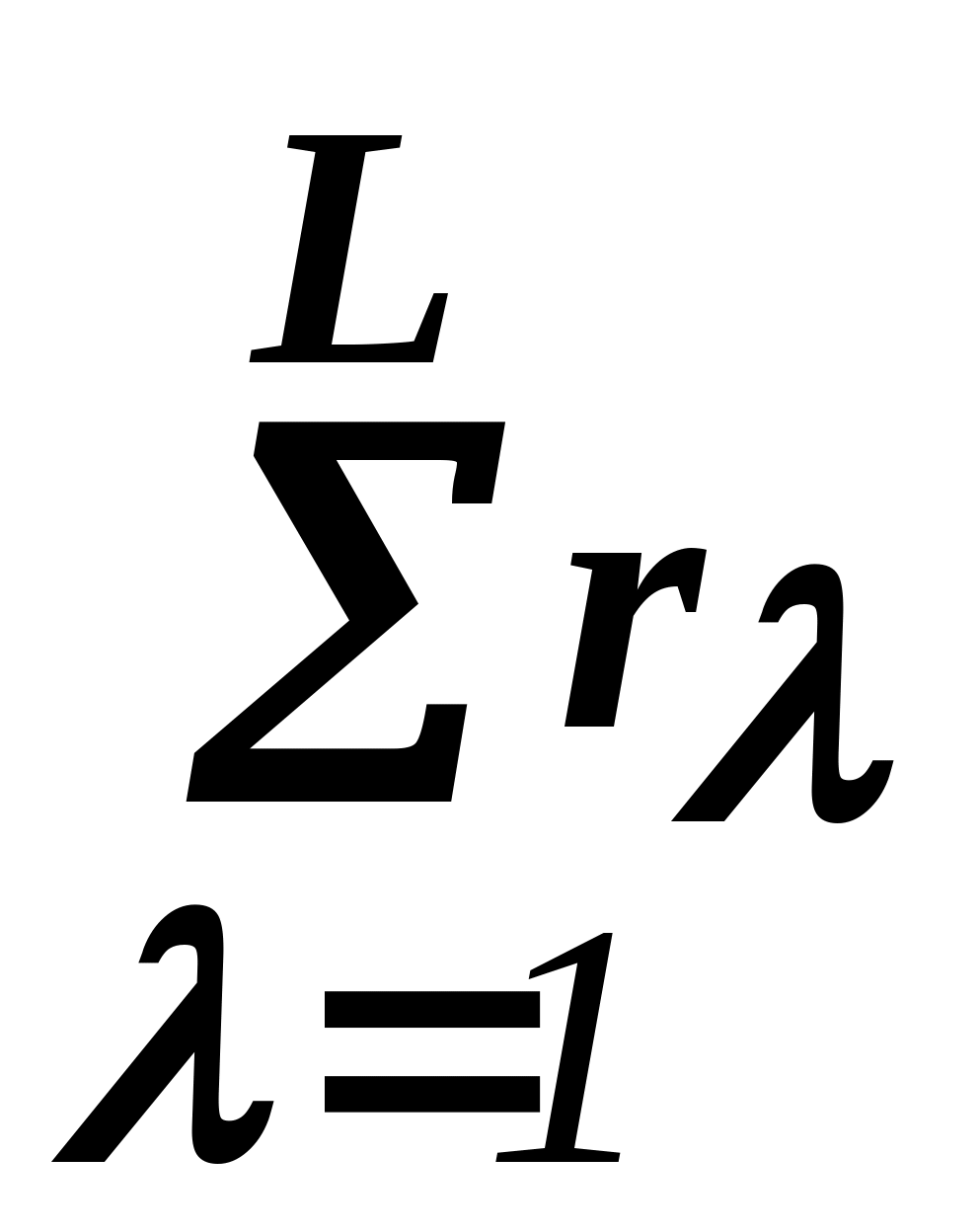 !
!
Добавилось же только одно -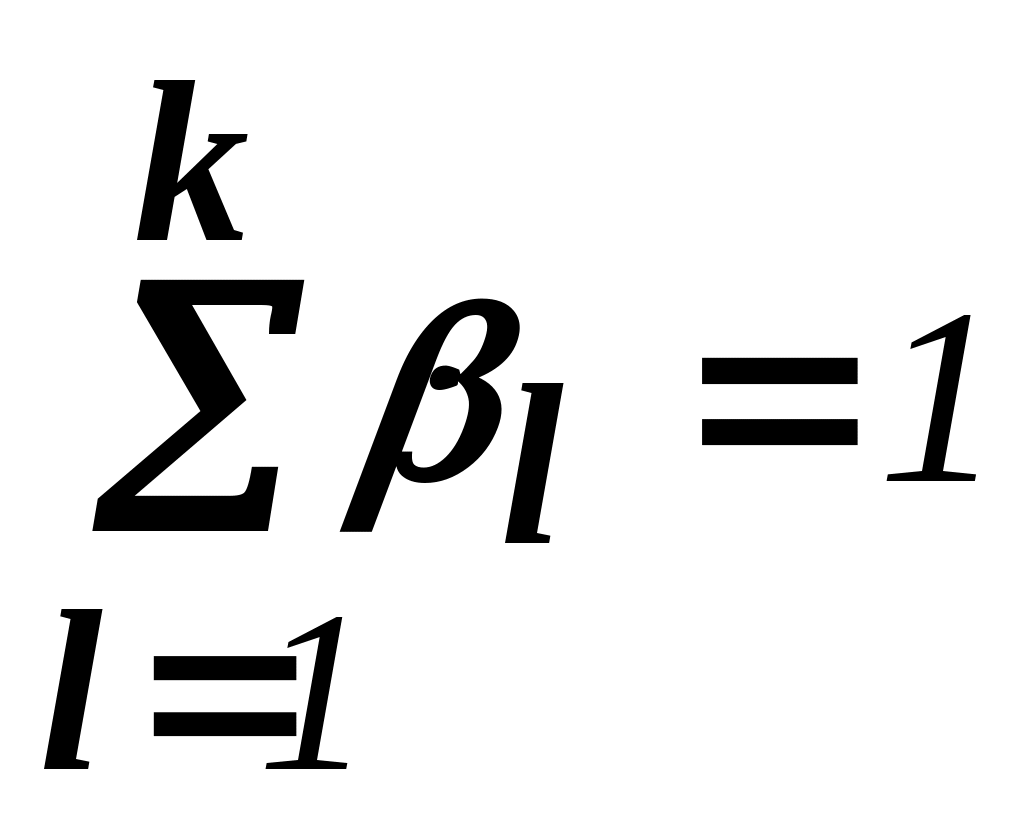 .
.
Но в новой задаче появились новые переменные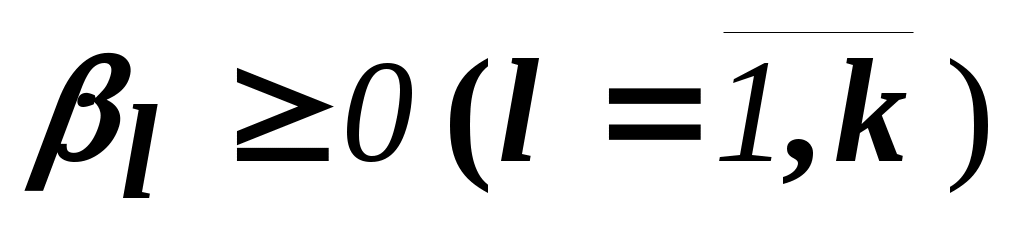 . Их количество - количество всех вершин!!!
. Их количество - количество всех вершин!!!
Там не менее ясно, что найдя значения этих переменных, можно найти и решение исходной задачи:
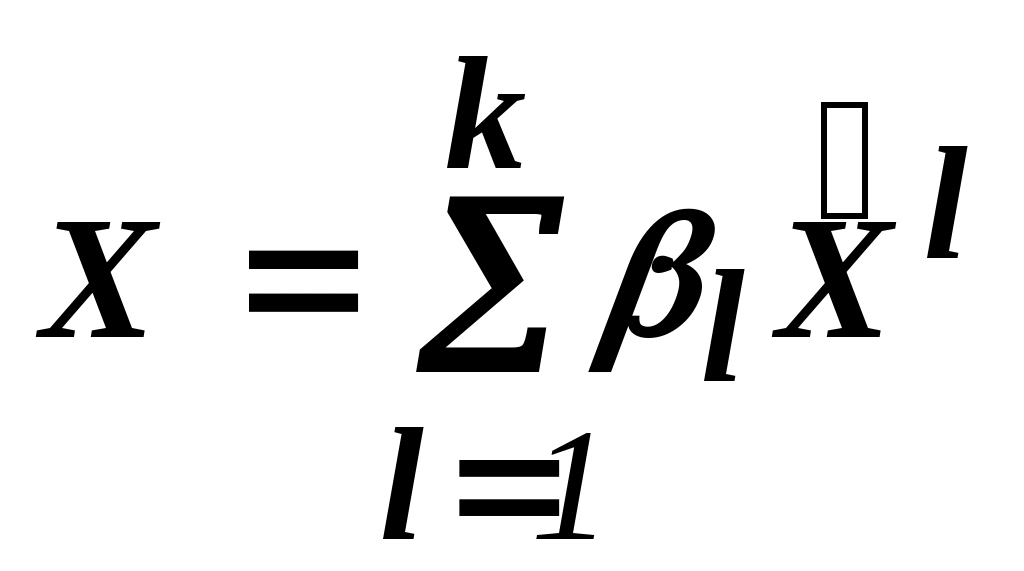 .
.
Определение. Задачу, соответствующую этой новой формулировке () будем называть главной, или, что то же самое, координирующей задачей.
Упростим обозначения:
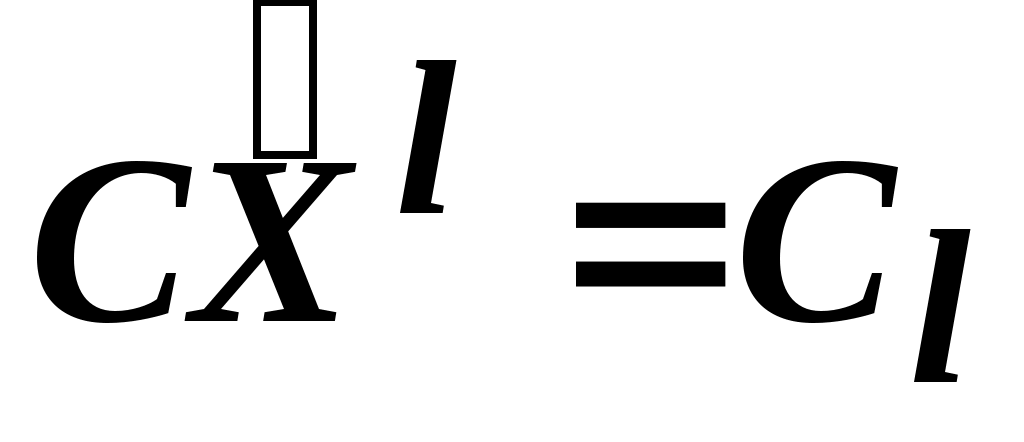
;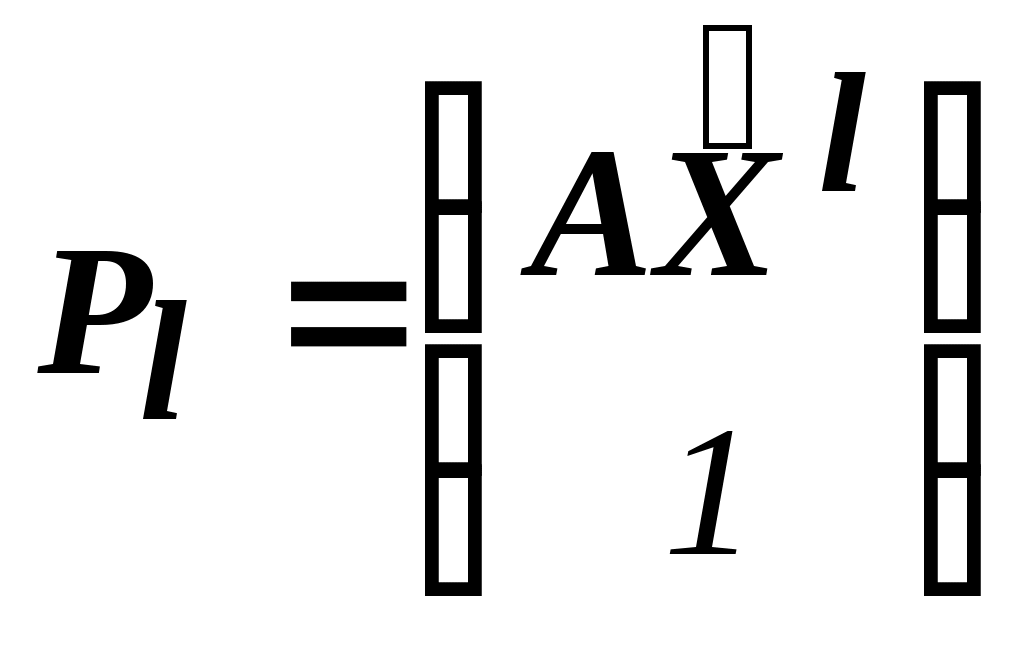 ;
; 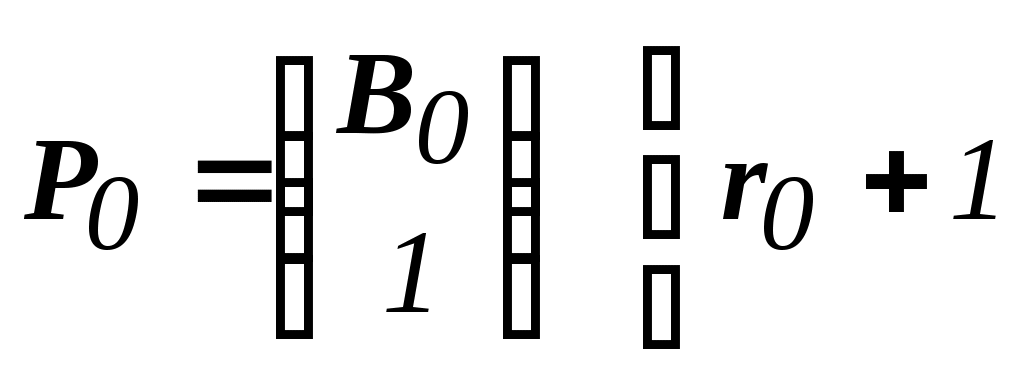
Пришли к следующей задаче:
()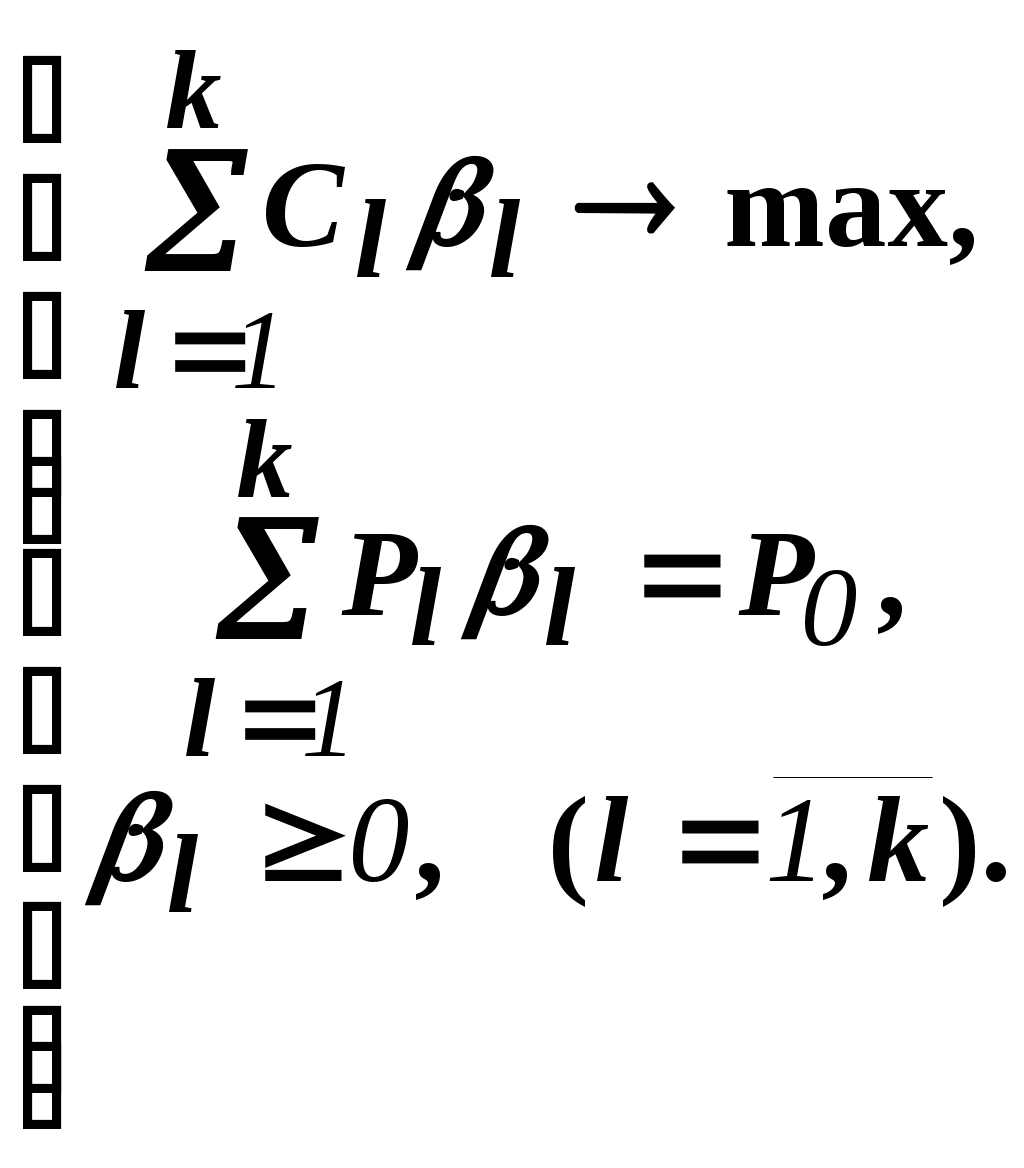
Несмотря на то, что вроде бы уже давно созрел "протест" против такой замены исходной задачи (блочно-диагональной структуры) координирующей задачей, рассмотрим конкретный пример построения координирующей задачи.
Пример.
2x1+3x2max,
x1+x2 15,
-3x1+x2 9,
4x1 +x2 8,
x1,2 0.
Будем считать, что блок-связка в этой задаче представлен единственным (первым) ограничением. Диагональный блок - вторым и третьим ограничениями. Т.е.:
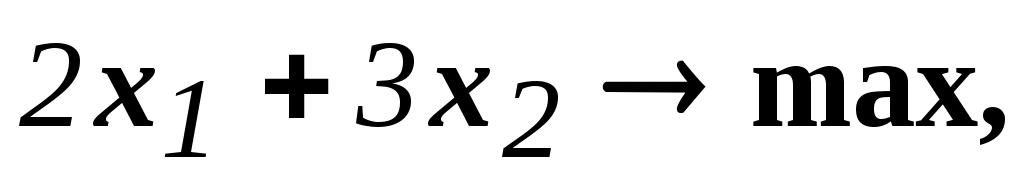 <c,x> max : C=(2,3)
<c,x> max : C=(2,3)
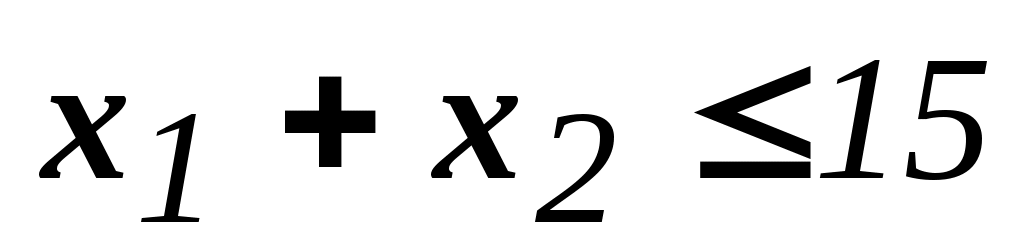
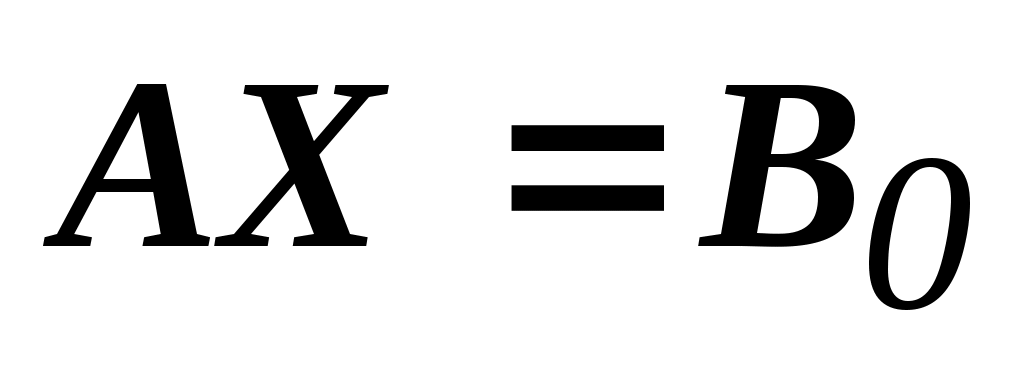 : A=(1,1); B0=(15)
: A=(1,1); B0=(15)
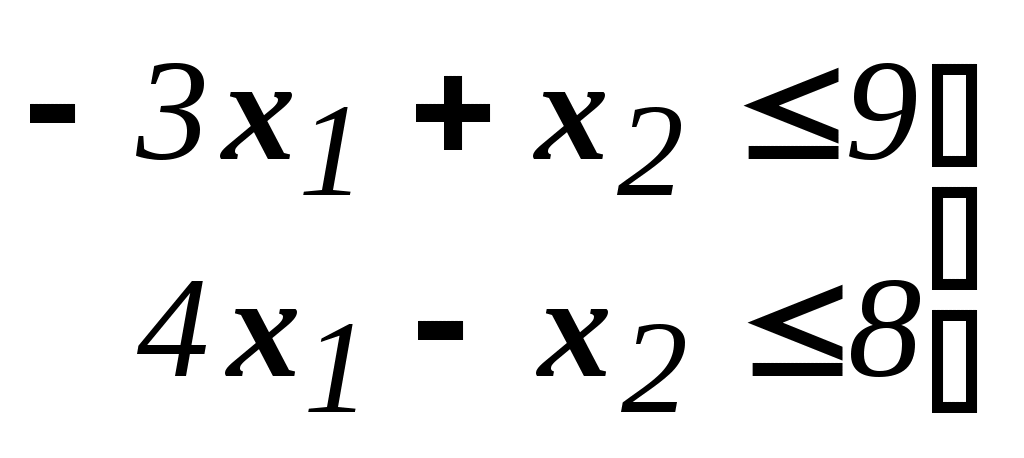
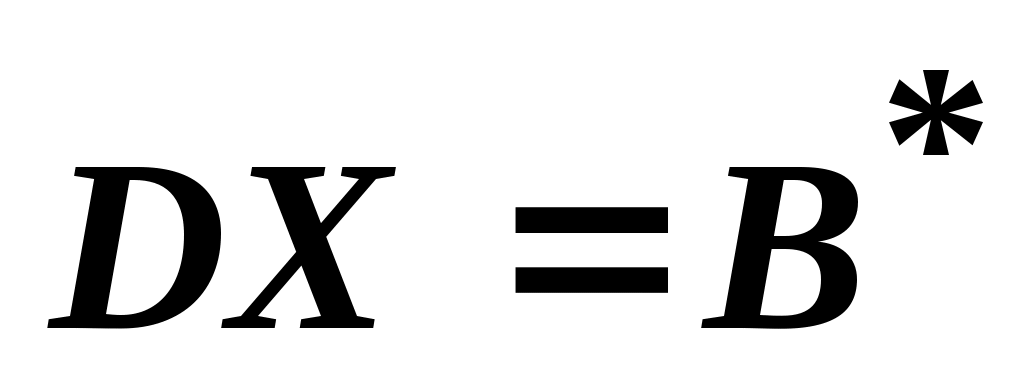 :
: 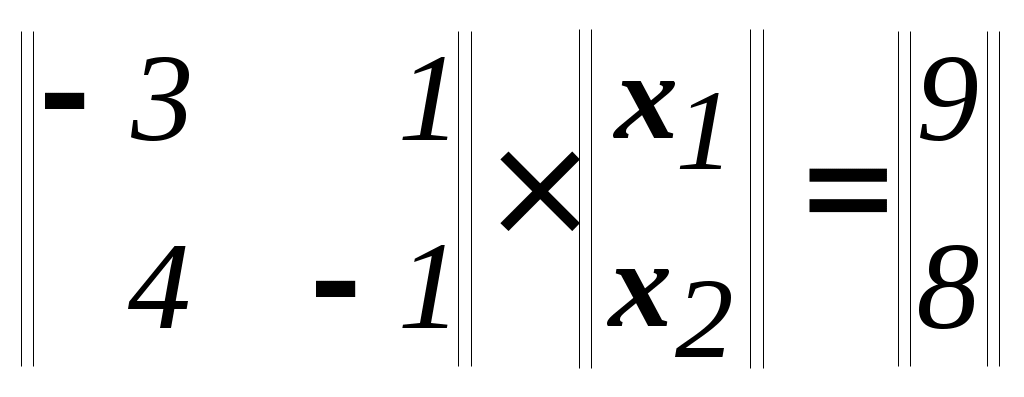
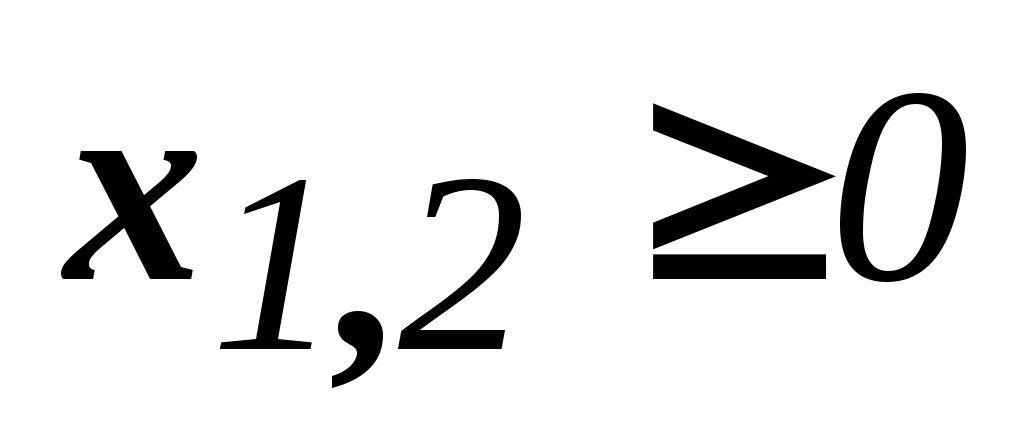 x 0
x 0
Множество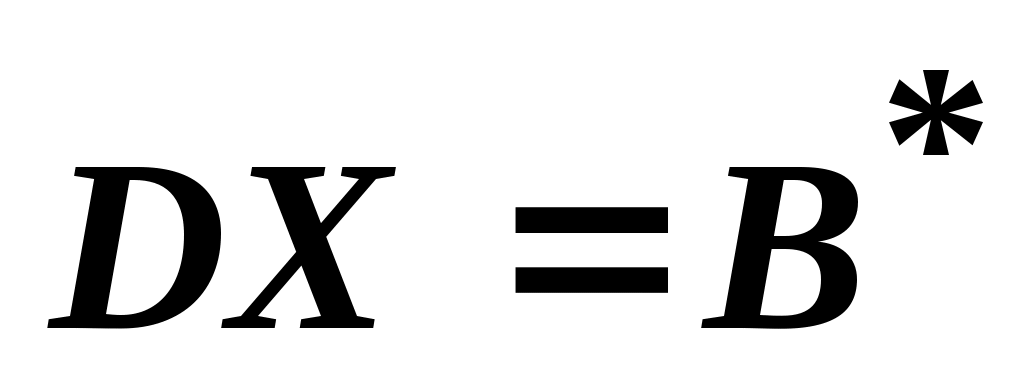 , x 0 имеет 4 вершины:
, x 0 имеет 4 вершины:
 =(0,0) C1=((2,3),(0,0))=0 //
=(0,0) C1=((2,3),(0,0))=0 // 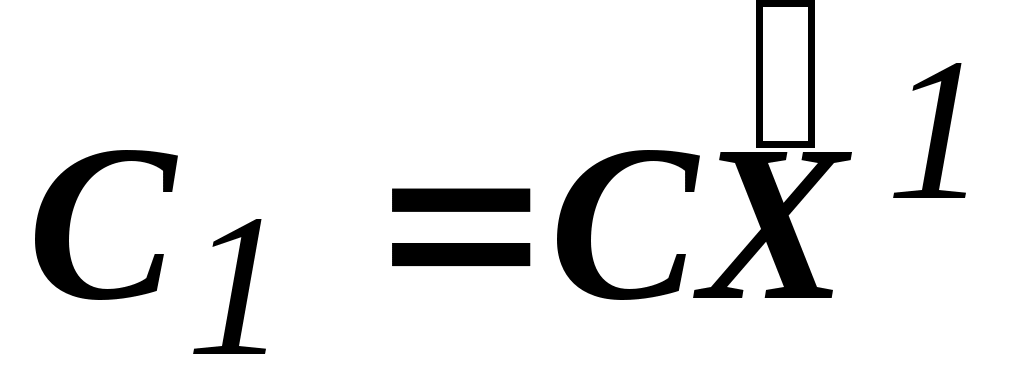 =0
=0
 =(0,9) C2=((2,3),(0,9))=27 //
=(0,9) C2=((2,3),(0,9))=27 // 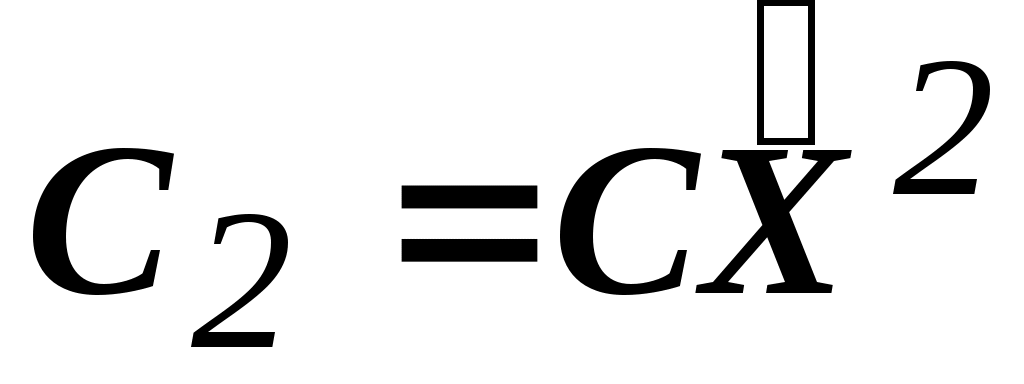 =27
=27
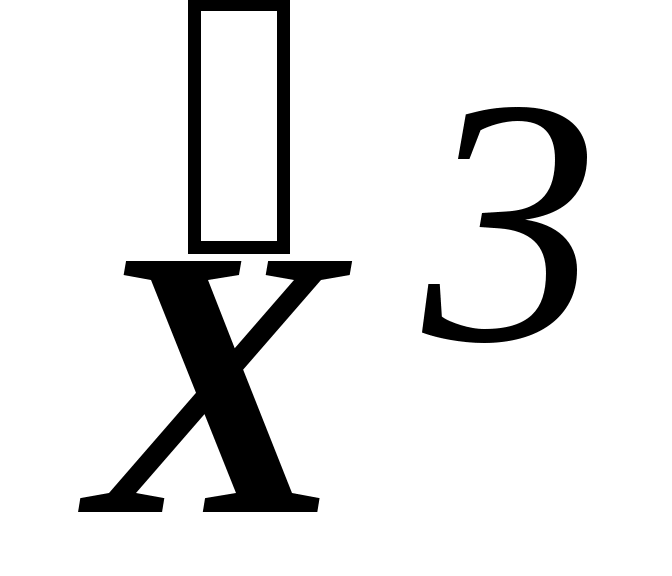 =(17,60) C3=((2,3),(17,60))=214 //
=(17,60) C3=((2,3),(17,60))=214 // 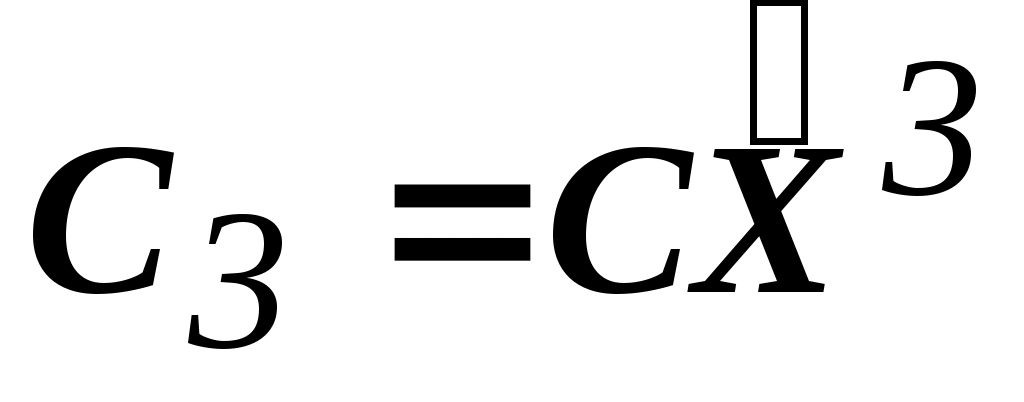 =214
=214
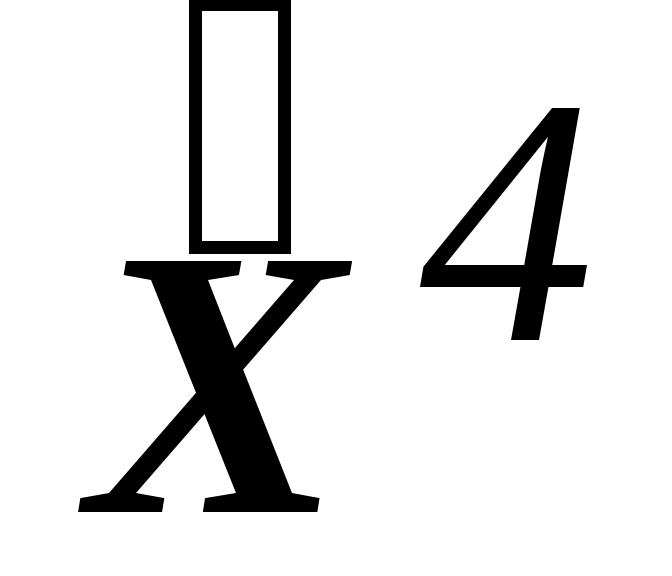
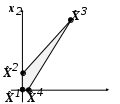 =(2,0) C4=((2,3),(2,0))=4 //
=(2,0) C4=((2,3),(2,0))=4 // 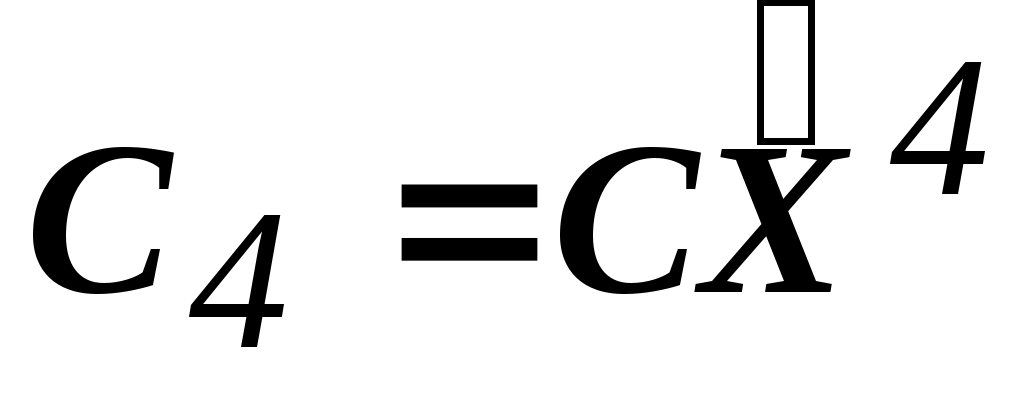 =4
=4
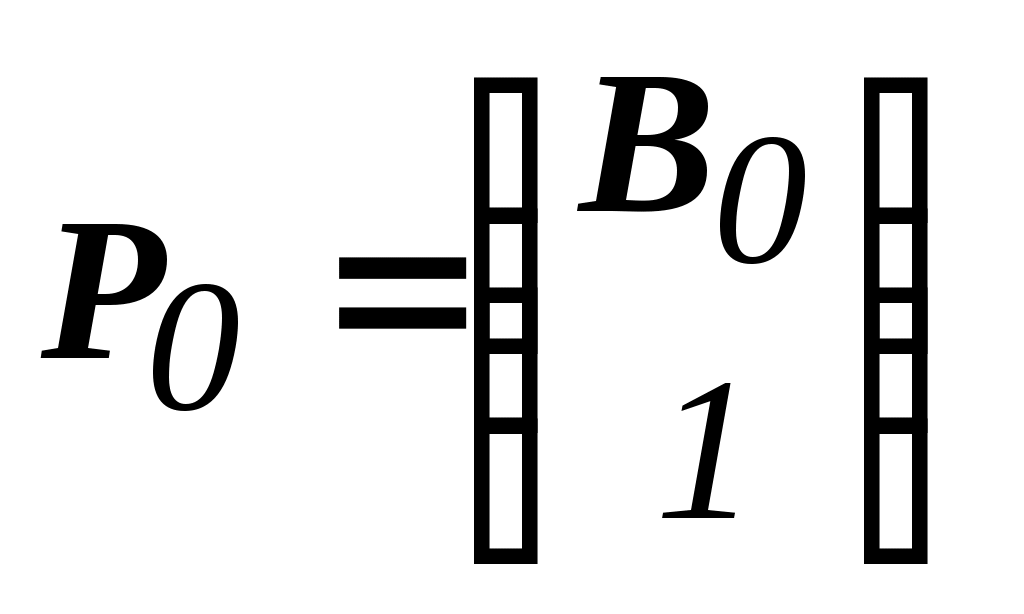 =
= .
.
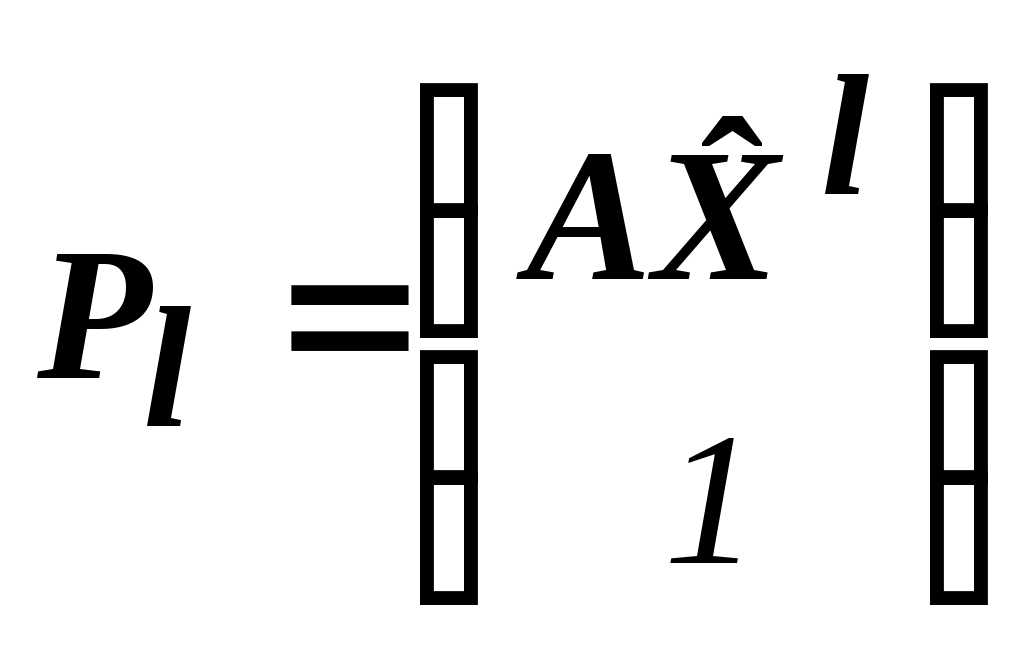 :
: 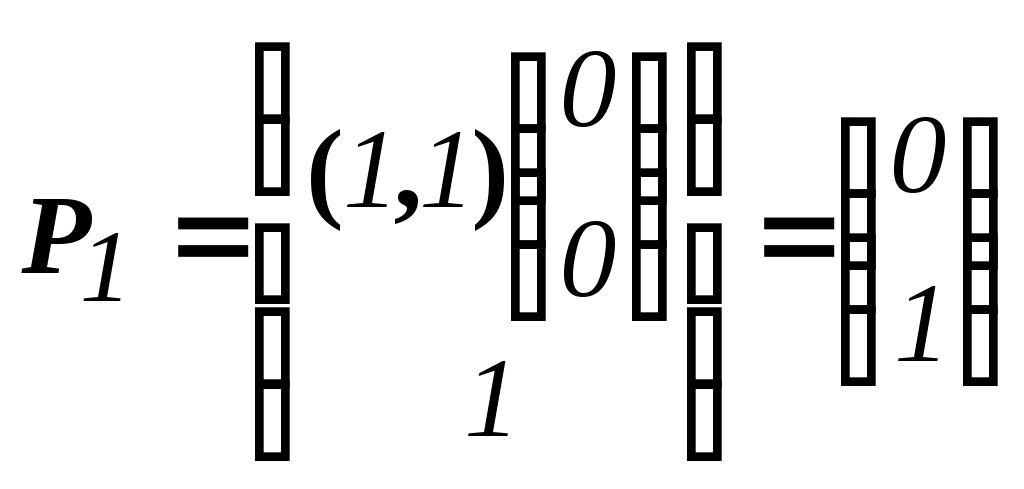 ;
; 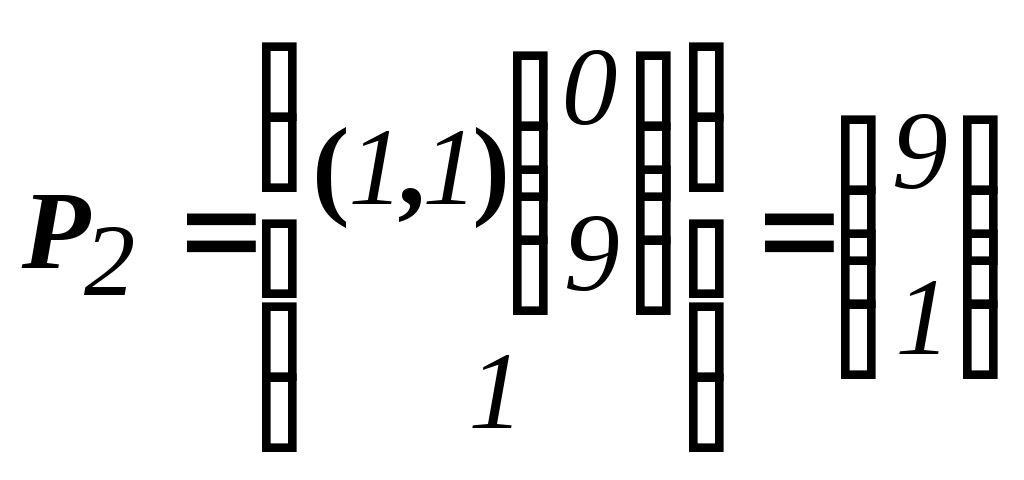 ;
;
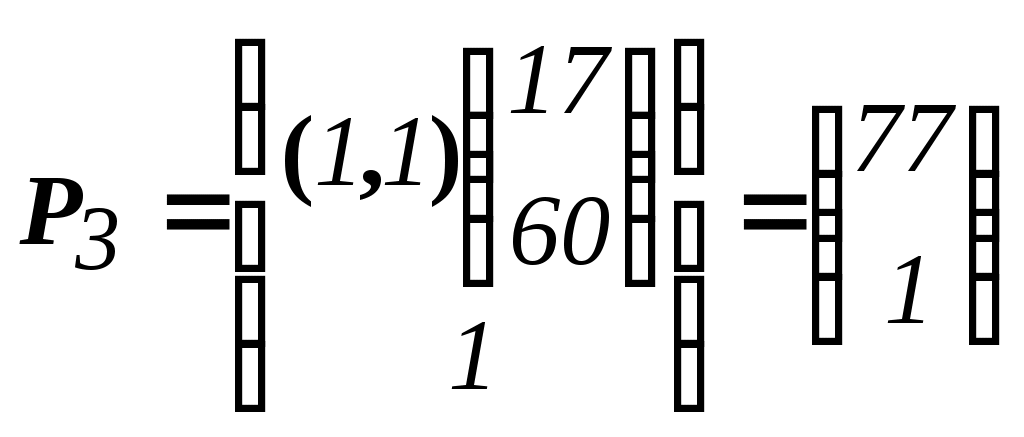 ;
; 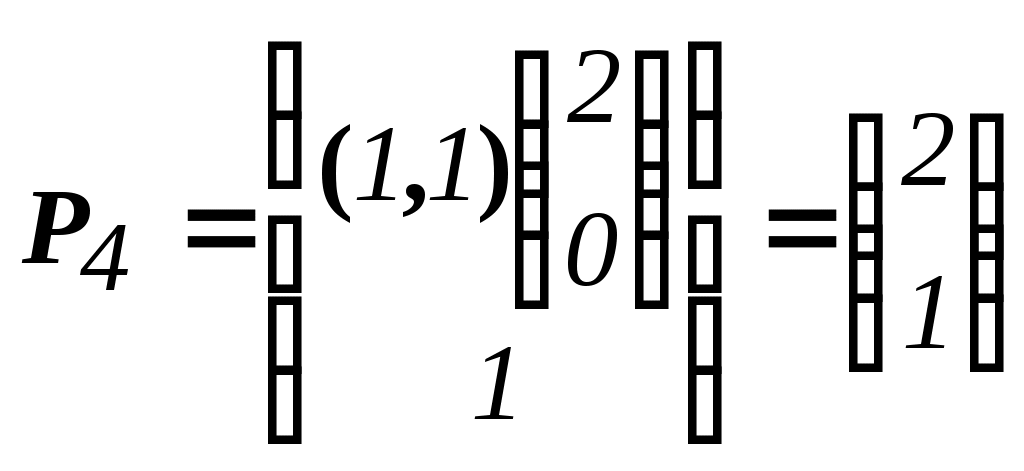 .
.
Координирующая задача имеет вид:
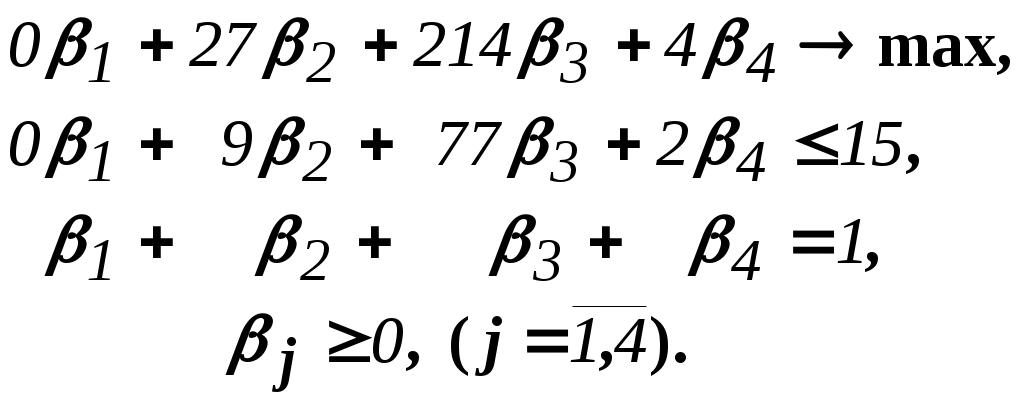
Какие можно сделать выводы?
Если сравнить исходную и главную задачи, можно заметить, что исходная задача имеет 3 ограничения и 2 переменные, а главная - 2 ограничения и 4 переменные. В принципе, уменьшение количества ограничений - это хорошо, так как не раз подчеркивалось, что методы ЛП весьма чувствительны к именно к количеству ограничений.
Но количество переменных возросло. Нам потребовалось вычислить координаты всех (!) вершин многоугольника, соответствующего диагональному блоку.
Мы уже говорили о том, что рассматриваемый метод декомпозиции2 ориентирован на решение задач очень большой размерности.
Естественно, что для вычисления координат всех вершин требуется не реализуемая мощность ЭВМ. Короче - это "безнадежное" дело. Так стоит ли игра свеч?
Вулф и Данциг - авторы метода декомпозиции - доказали, что решение главной задачи можно искать не зная ни всех вершин многогранника, определенного диагональным блоком, ни (даже!) количества этих вершин.
Достаточно знать лишь один (любой) опорный план главной задачи, а также базисную и обратную к ней матрицы соответствующего опорного решения.
При этом (что самое важное в методе), координирующая задача в явном виде нигде не записывается3.
Остановимся на этом методе подробнее.
Итак, представим себе главную задачу:
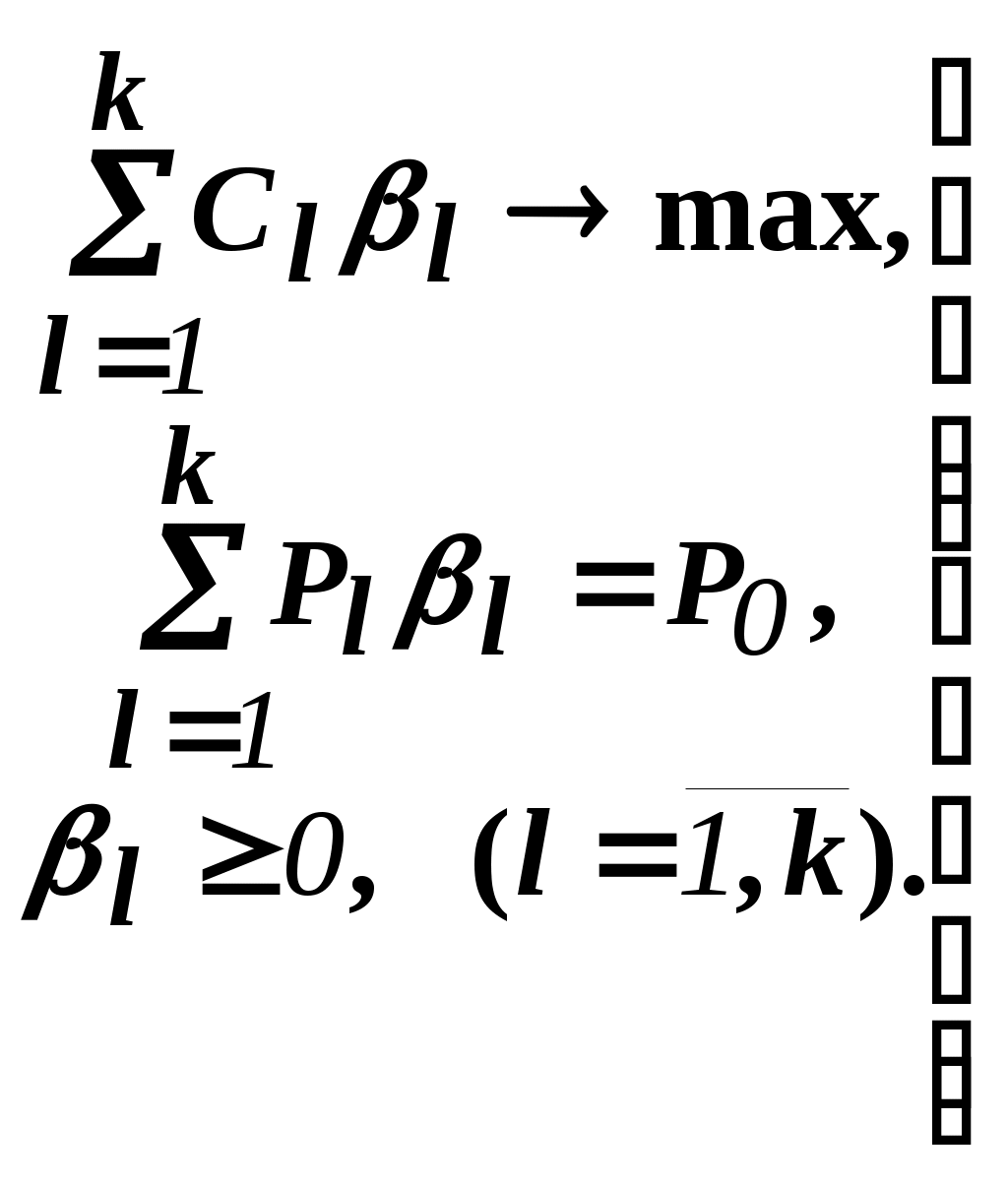 Здесь
Здесь 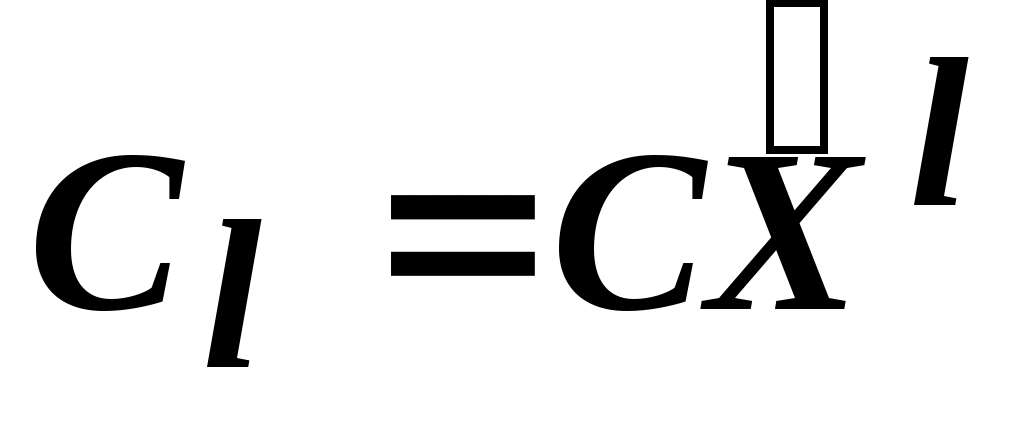 ;
;  ;
; 
Пусть:
B - базисная матрица некоторого опорного решения этой задачи;
B-1 - обратная матрица;
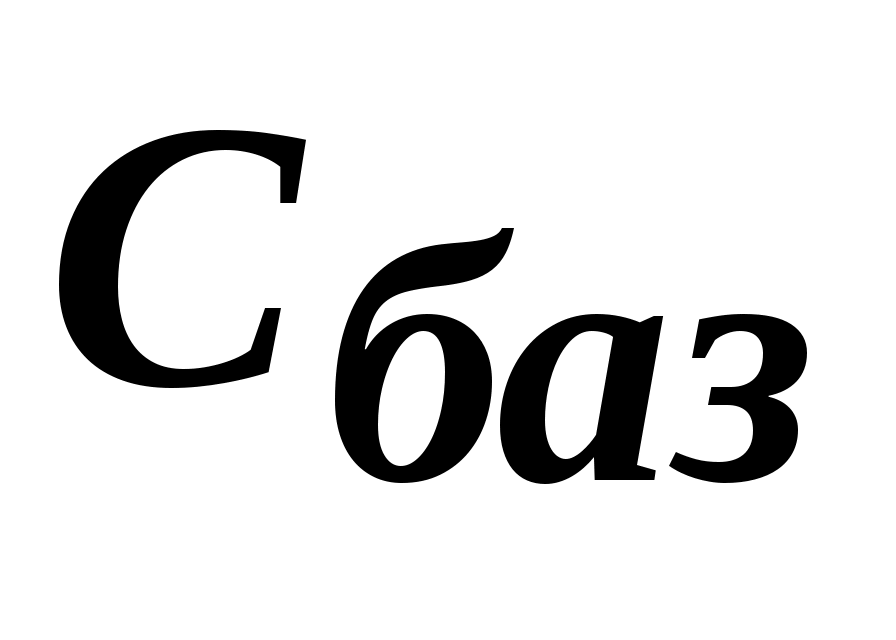 - вектор коэффициентов ЦФ при базисных переменных.
- вектор коэффициентов ЦФ при базисных переменных.
В соответствии с вычислительной схемой модифицированного симплекс-метода4 (МСМ) текущее решение является оптимальным, если для всех небазисных векторов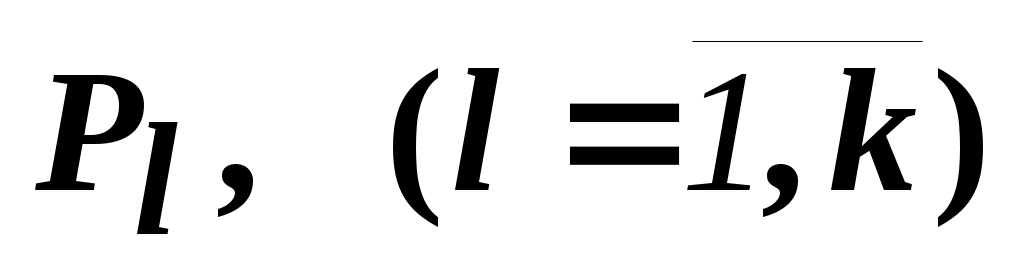 оценки этих векторов не отрицательны:
оценки этих векторов не отрицательны:
Начнем анализ этого выражения на предмет исследования возможности его практического использования.
Прежде всего "разберемся" с произведением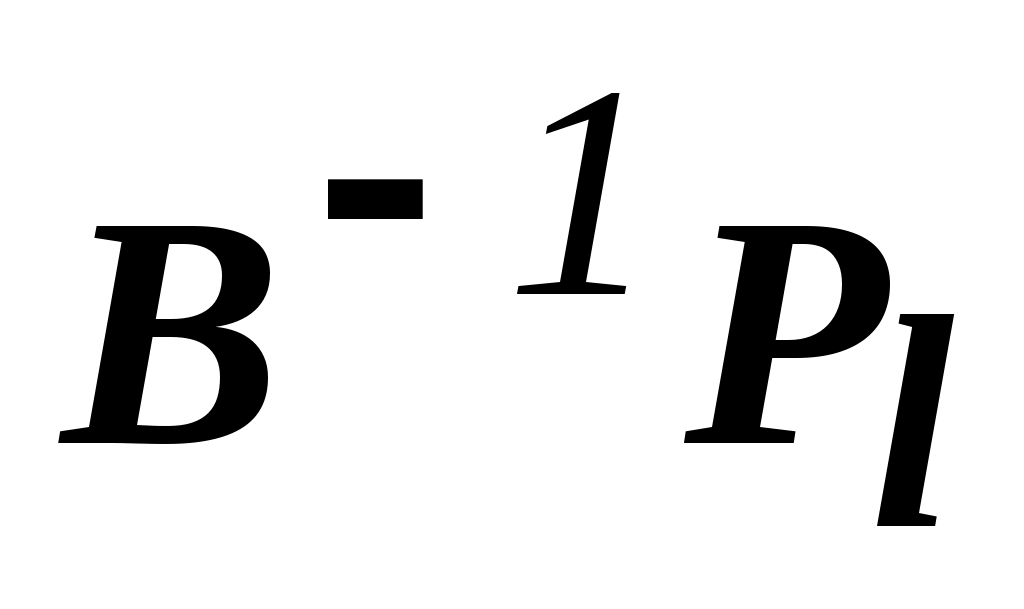 5
5
Подставим (2) в (1):
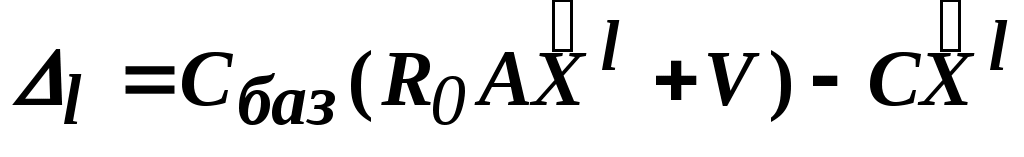 -оценка вектора
-оценка вектора 
или
(3)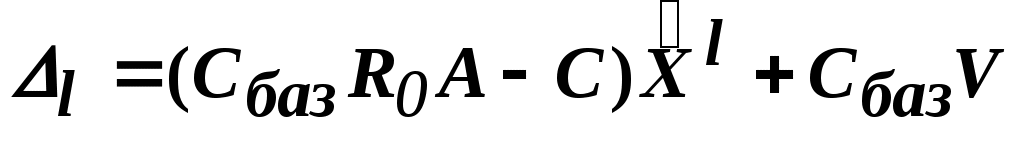
Самое интересное начинается здесь!
Известно, что если решение не оптимальное, вектор Pl , которому соответствует отрицательная оценка (желательно, максимальная по абсолютной величине), должен быть включен в состав базисных векторов.
Проблема же в том, что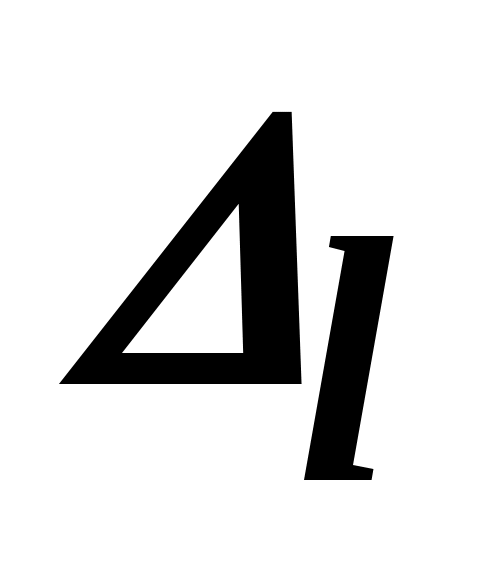 нельзя вычислить до тех пор, пока не известны все элементы вектора
нельзя вычислить до тех пор, пока не известны все элементы вектора 
.
В свою очередь, численное определение этих элементов невозможно до тех пор, пока не известна соответствующая экстремальная точка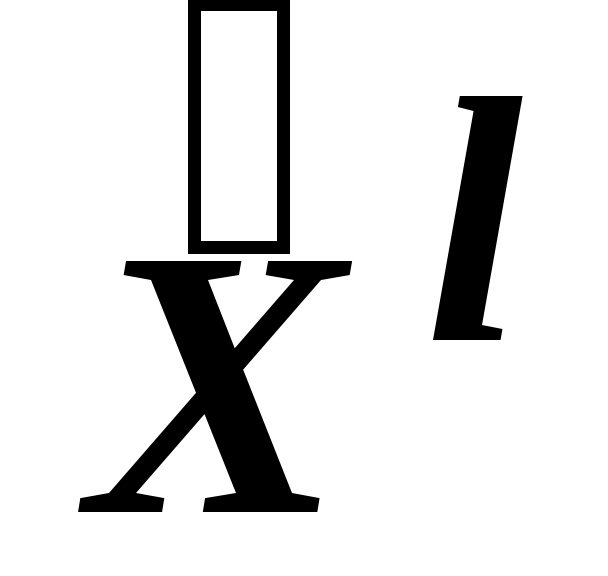 .
.
То есть, нужно сначала определить эту экстремальную точку. А как ее определить, если мы знаем только обратную матрицу главной задачи B-1 и Сбаз. Сама же задача задана неявно. Ее просто нет!
Идея метода Данцига - Вулфа заключается в том, чтобы заменить поиск отрицательной оценки путем последовательного перебора свободных векторов текущего опорного решения направленным поиском только одной экстремальной точки, которой соответствует минимальная оценка связанного с этой точкой вектора главной задачи.
Если окажется, что найденная таким образом минимальная оценка неотрицательна, задача решена. Точнее, решена главная задача, а следовательно - и исходная.
В противном случае ясно, какой вектор следует вводить в базис: этот вектор будет полностью определен координатами найденной экстремальной точки.
Итак, нужно найти экстремальную точку, которой соответствует вектор главной задачи, имеющий минимальную оценку.
Это можно сделать, решив следующую задачу:
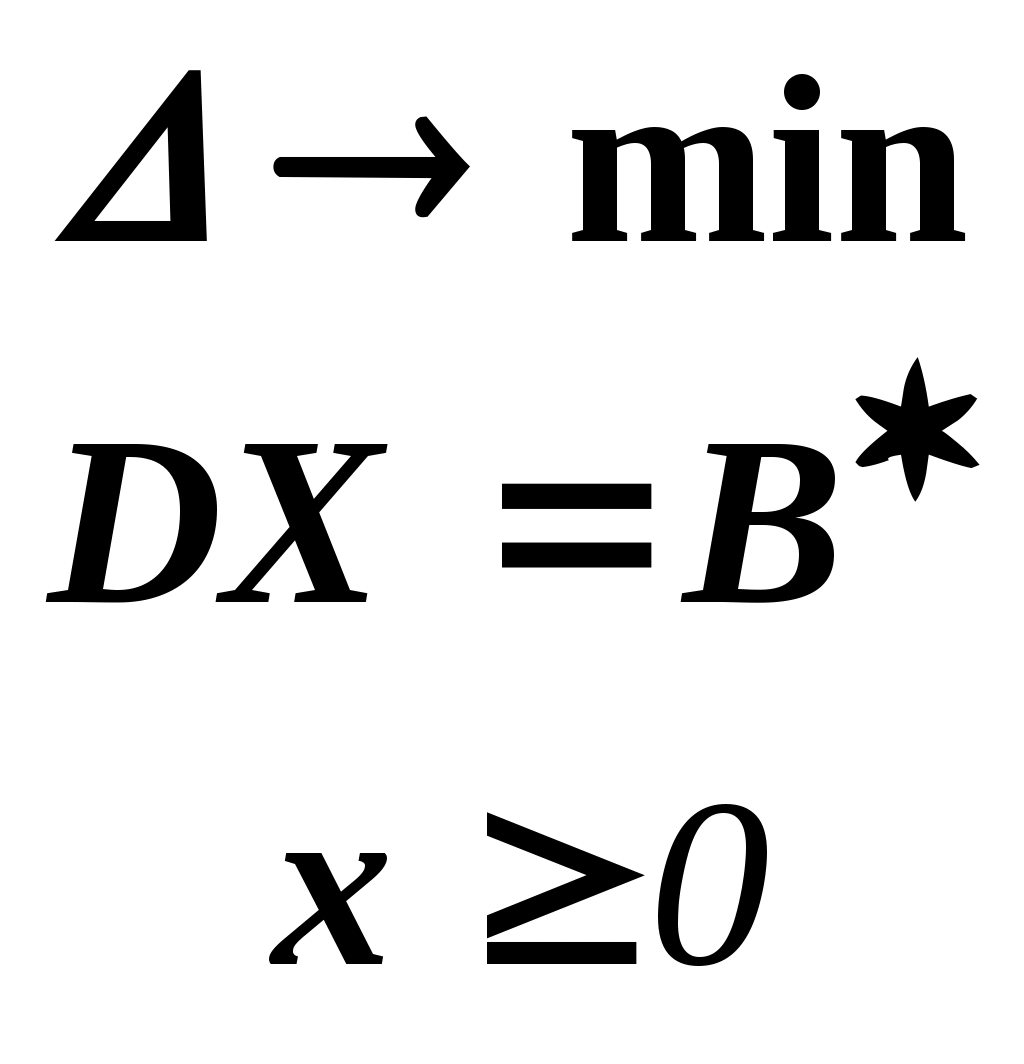
Здесь следует обратить внимание на то, что индекс номера вершины отсутствует. Этот индекс просто неизвестен, т.к. соответствующую вершину еще нужно найти.
В качестве переменных этой задачи выступают координаты искомой вершины.
Мы предположили, что множество, определенное ограничениями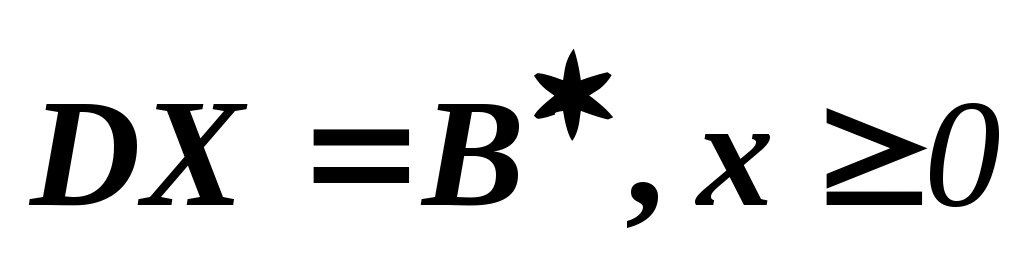 , ограничено. Следовательно, минимальное значение также ограничено и должно соответствовать некоторой экстремальной точке. Ее то и нужно найти.
, ограничено. Следовательно, минимальное значение также ограничено и должно соответствовать некоторой экстремальной точке. Ее то и нужно найти.
Уже было показано, что:
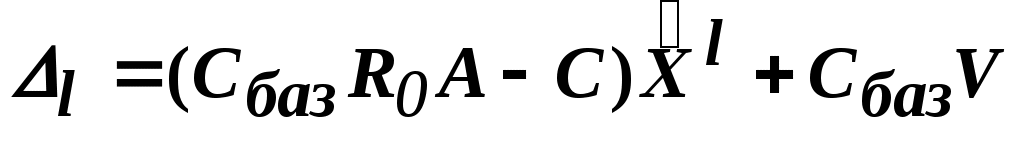 . (3)
. (3)
Теперь, опустив индекс l, имеем:
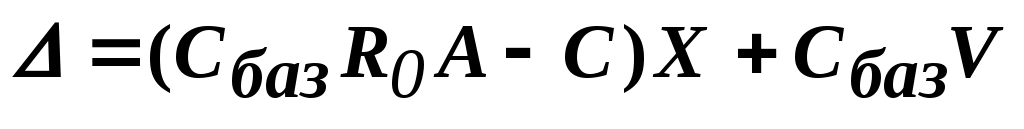 . (4)
. (4)
Ввиду того, что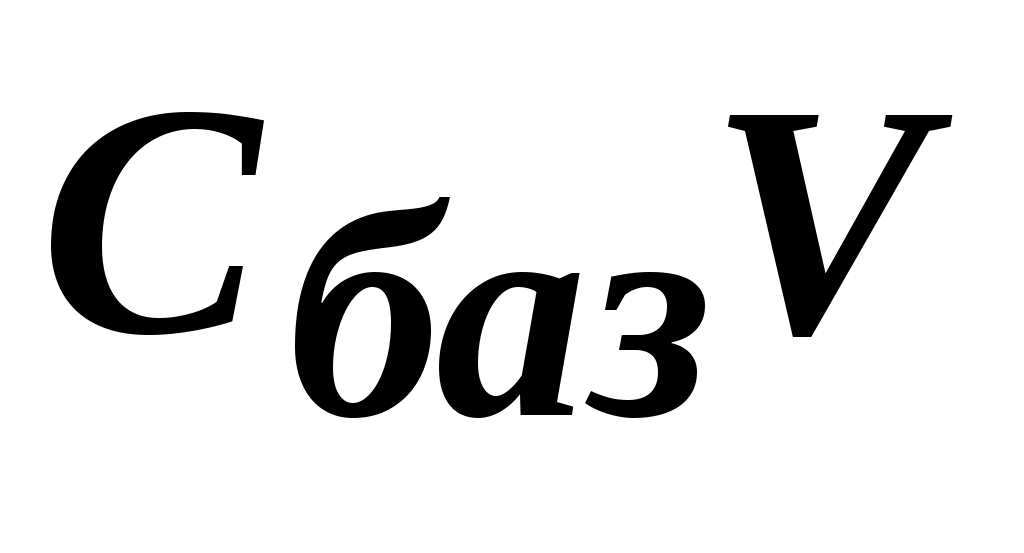 - постоянная величина, не зависящая от X , задаче ЛП можно придать следующий вид:
- постоянная величина, не зависящая от X , задаче ЛП можно придать следующий вид:
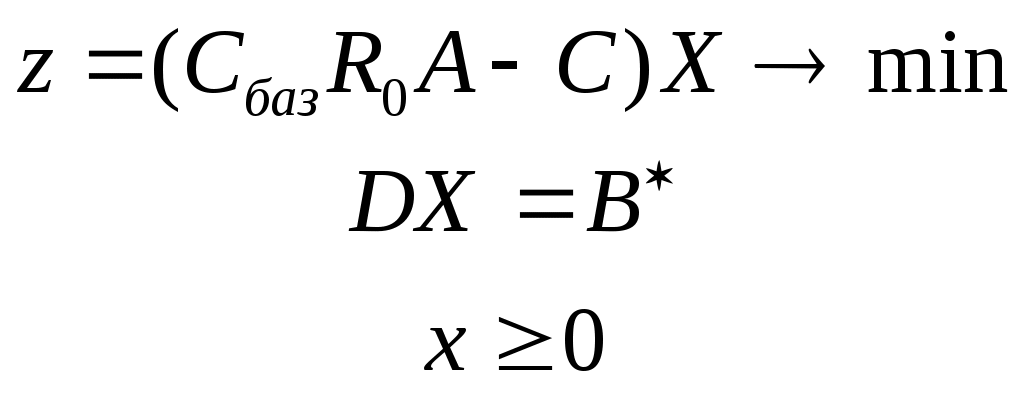
Очевидно, что любая точка, представленная в виде (), удовлетворяет всем ограничениям
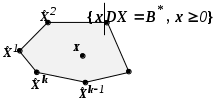
Здесь
Это обстоятельство позволяет видоизменить исходную задачу таким образом, что из рассмотрения будут исключены все ограничения диагонального блока.
Примем обозначения:
А=(А1,А2, ... ,Аn) - матрица, составленная из векторов блока-связки.
Теперь задача приобретает следующий вид:
()
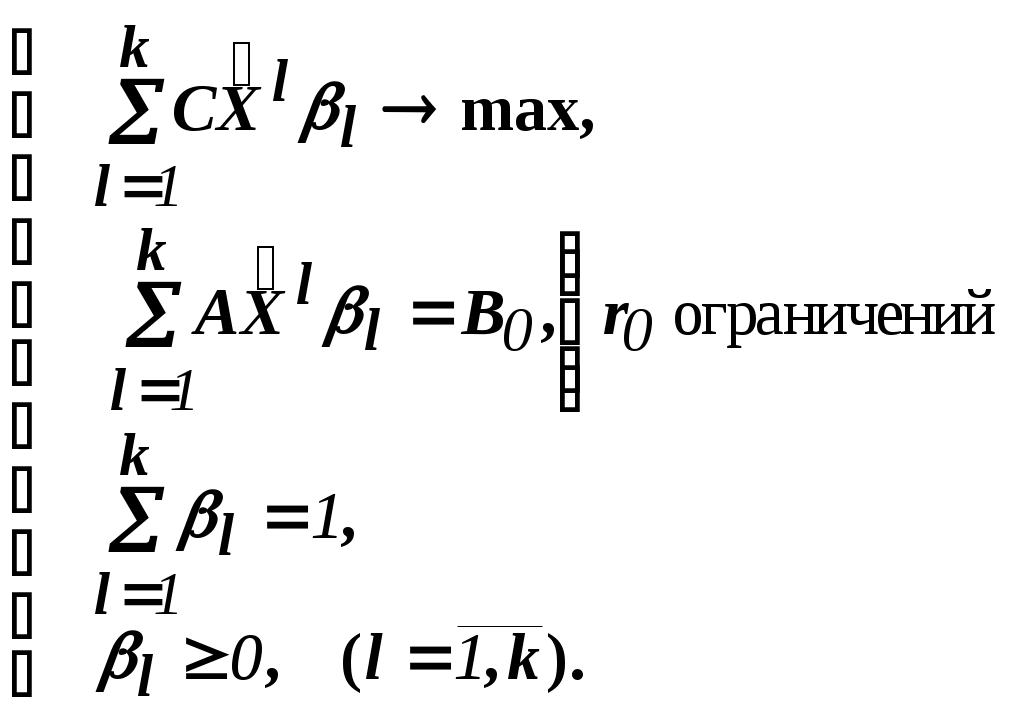

Как видно, все ограничения, составляющие диагональный блок
Добавилось же только одно -
Но в новой задаче появились новые переменные
Там не менее ясно, что найдя значения этих переменных, можно найти и решение исходной задачи:
Определение. Задачу, соответствующую этой новой формулировке () будем называть главной, или, что то же самое, координирующей задачей.
Упростим обозначения:
;
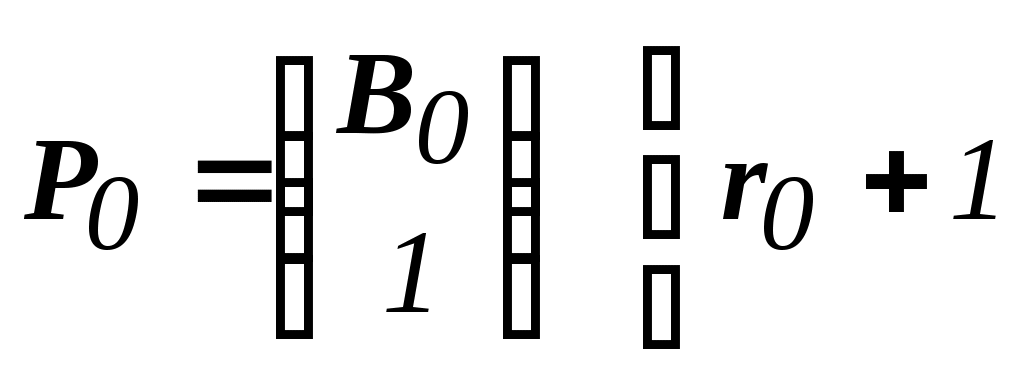
Пришли к следующей задаче:
()
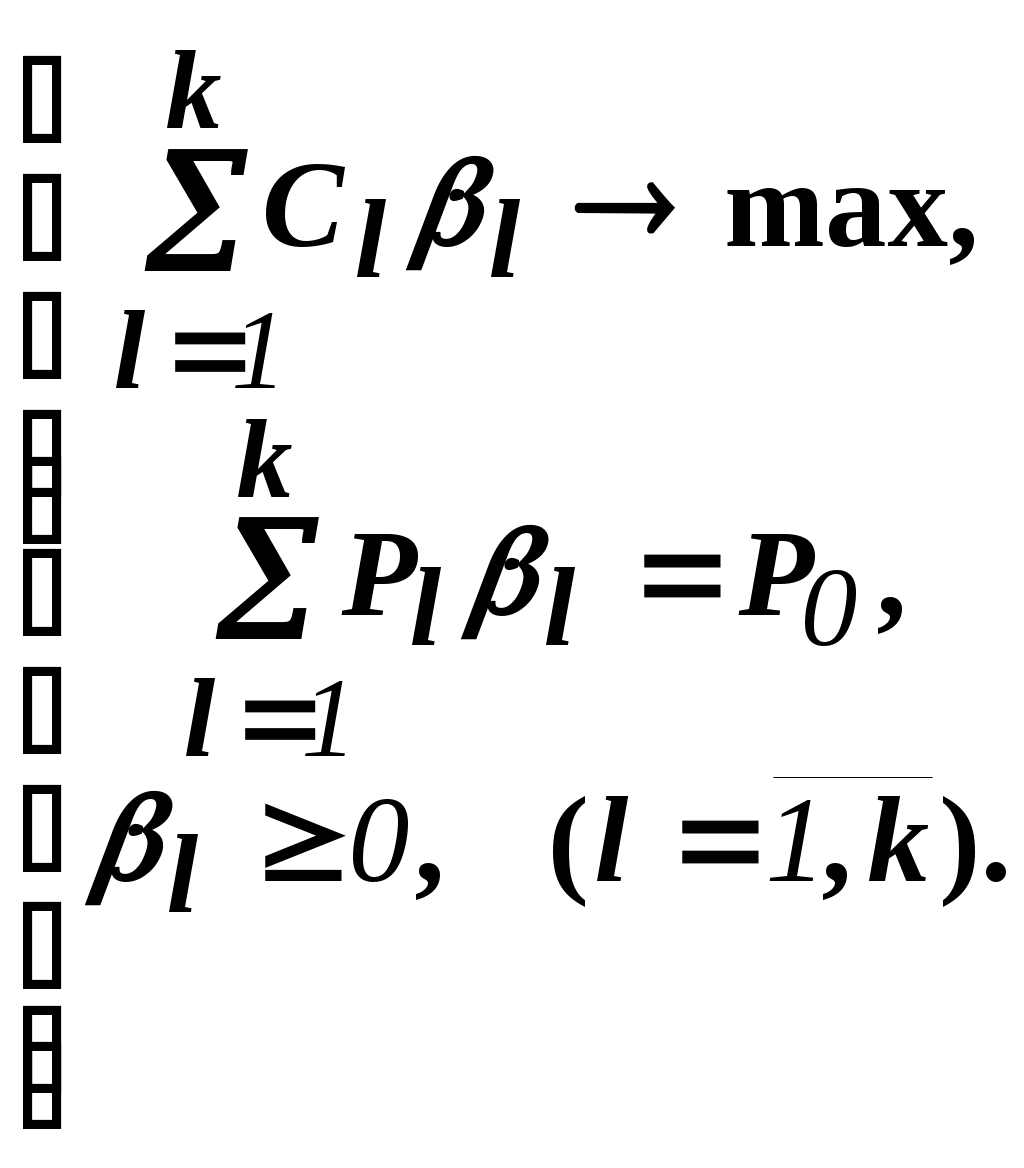
Несмотря на то, что вроде бы уже давно созрел "протест" против такой замены исходной задачи (блочно-диагональной структуры) координирующей задачей, рассмотрим конкретный пример построения координирующей задачи.
Пример.
2x1+3x2max,
x1+x2 15,
-3x1+x2 9,
4x1 +x2 8,
x1,2 0.
Будем считать, что блок-связка в этой задаче представлен единственным (первым) ограничением. Диагональный блок - вторым и третьим ограничениями. Т.е.:
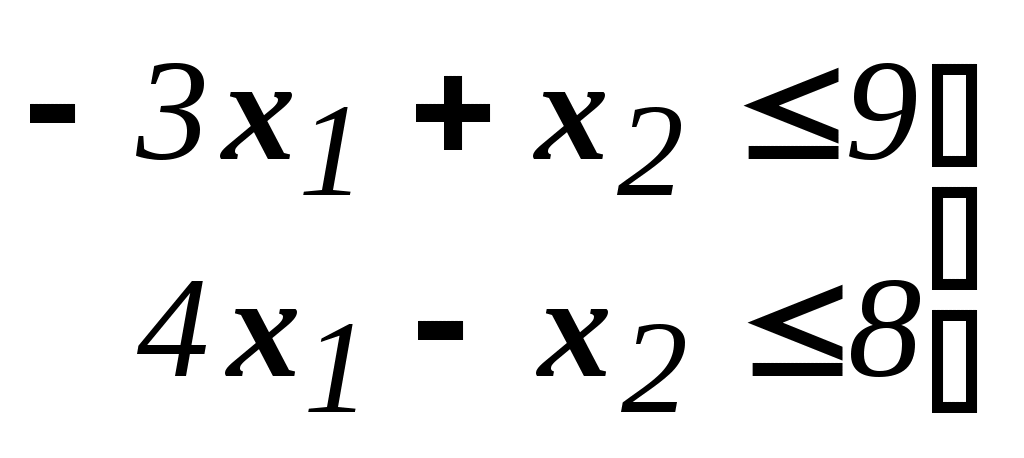
Множество
 =(2,0) C4=((2,3),(2,0))=4 //
=(2,0) C4=((2,3),(2,0))=4 // 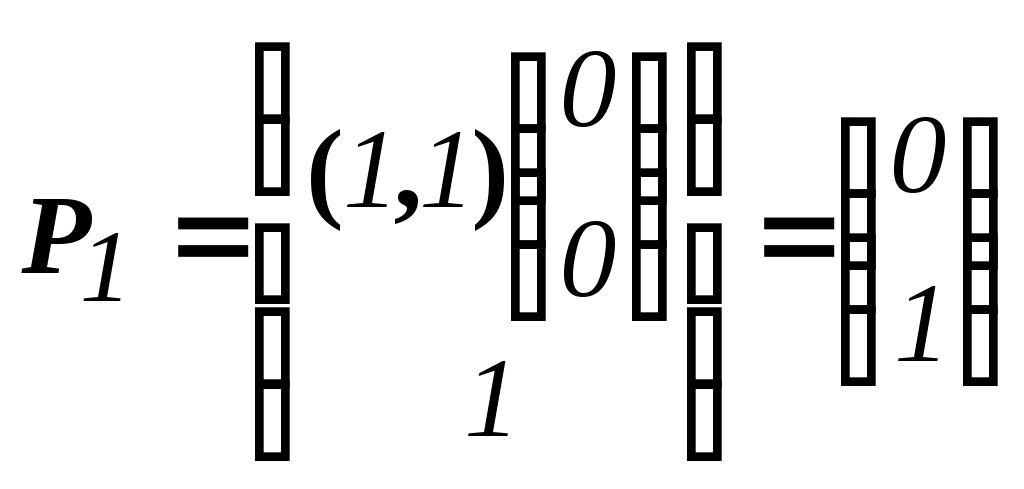 ;
; 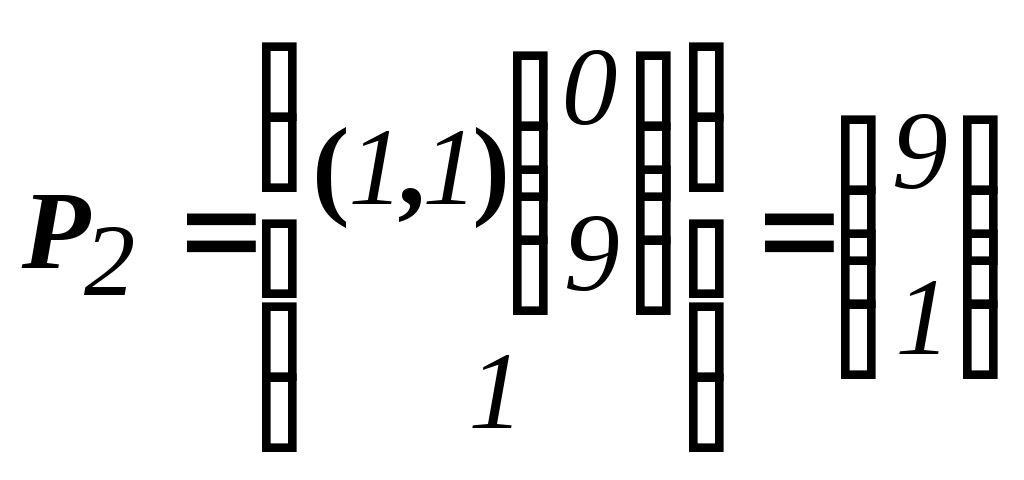 ;
;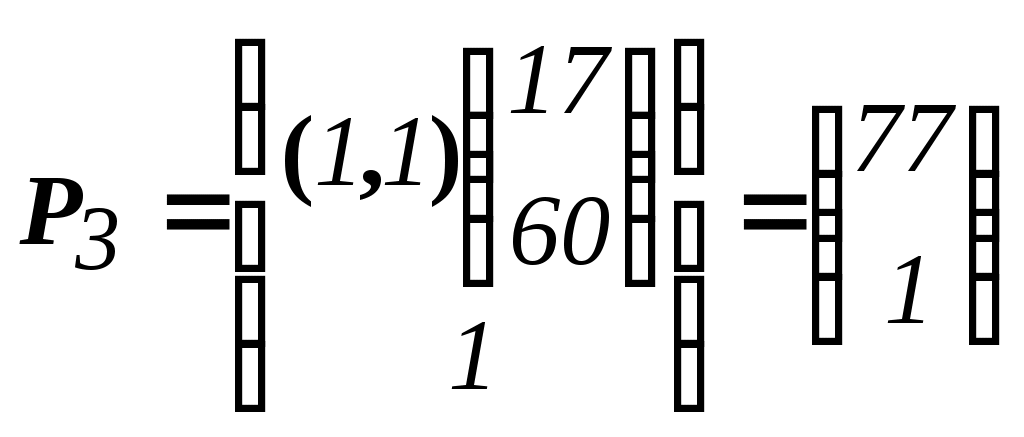 ;
; 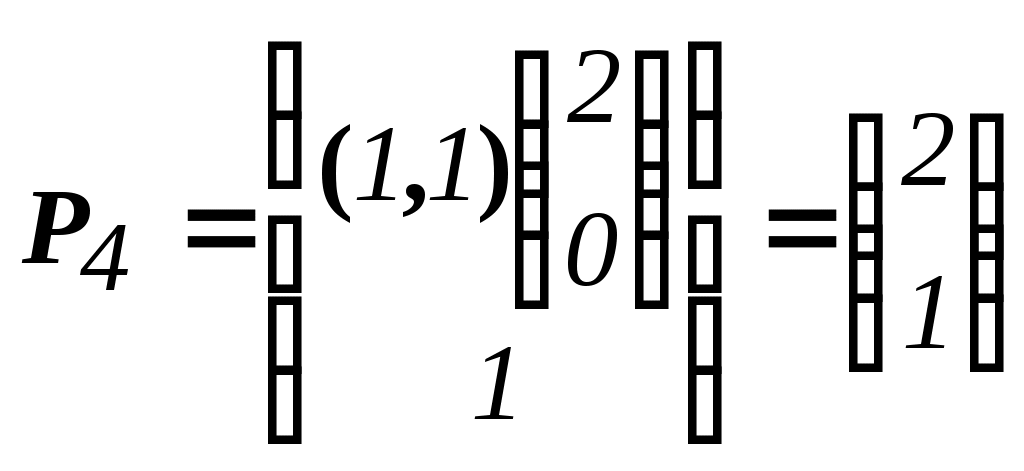 .
.Координирующая задача имеет вид:
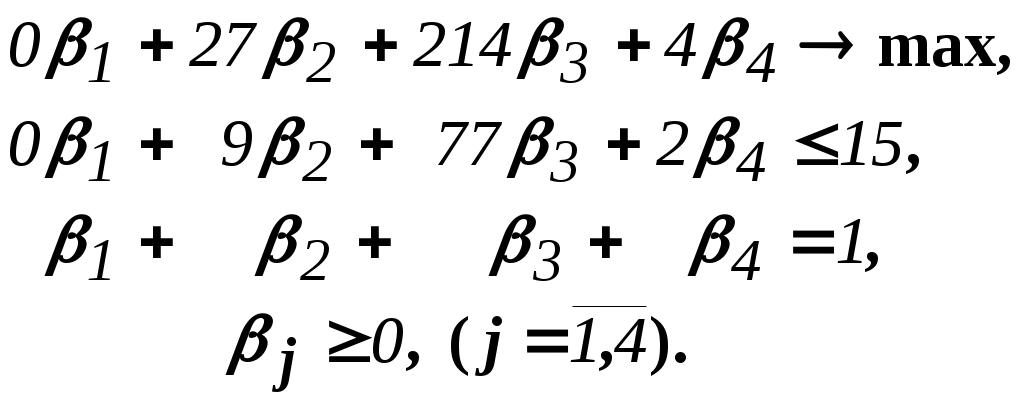
Какие можно сделать выводы?
Если сравнить исходную и главную задачи, можно заметить, что исходная задача имеет 3 ограничения и 2 переменные, а главная - 2 ограничения и 4 переменные. В принципе, уменьшение количества ограничений - это хорошо, так как не раз подчеркивалось, что методы ЛП весьма чувствительны к именно к количеству ограничений.
Но количество переменных возросло. Нам потребовалось вычислить координаты всех (!) вершин многоугольника, соответствующего диагональному блоку.
Мы уже говорили о том, что рассматриваемый метод декомпозиции2 ориентирован на решение задач очень большой размерности.
Естественно, что для вычисления координат всех вершин требуется не реализуемая мощность ЭВМ. Короче - это "безнадежное" дело. Так стоит ли игра свеч?
Вулф и Данциг - авторы метода декомпозиции - доказали, что решение главной задачи можно искать не зная ни всех вершин многогранника, определенного диагональным блоком, ни (даже!) количества этих вершин.
Достаточно знать лишь один (любой) опорный план главной задачи, а также базисную и обратную к ней матрицы соответствующего опорного решения.
При этом (что самое важное в методе), координирующая задача в явном виде нигде не записывается3.
Остановимся на этом методе подробнее.
Идея метода декомпозиции
Итак, представим себе главную задачу:
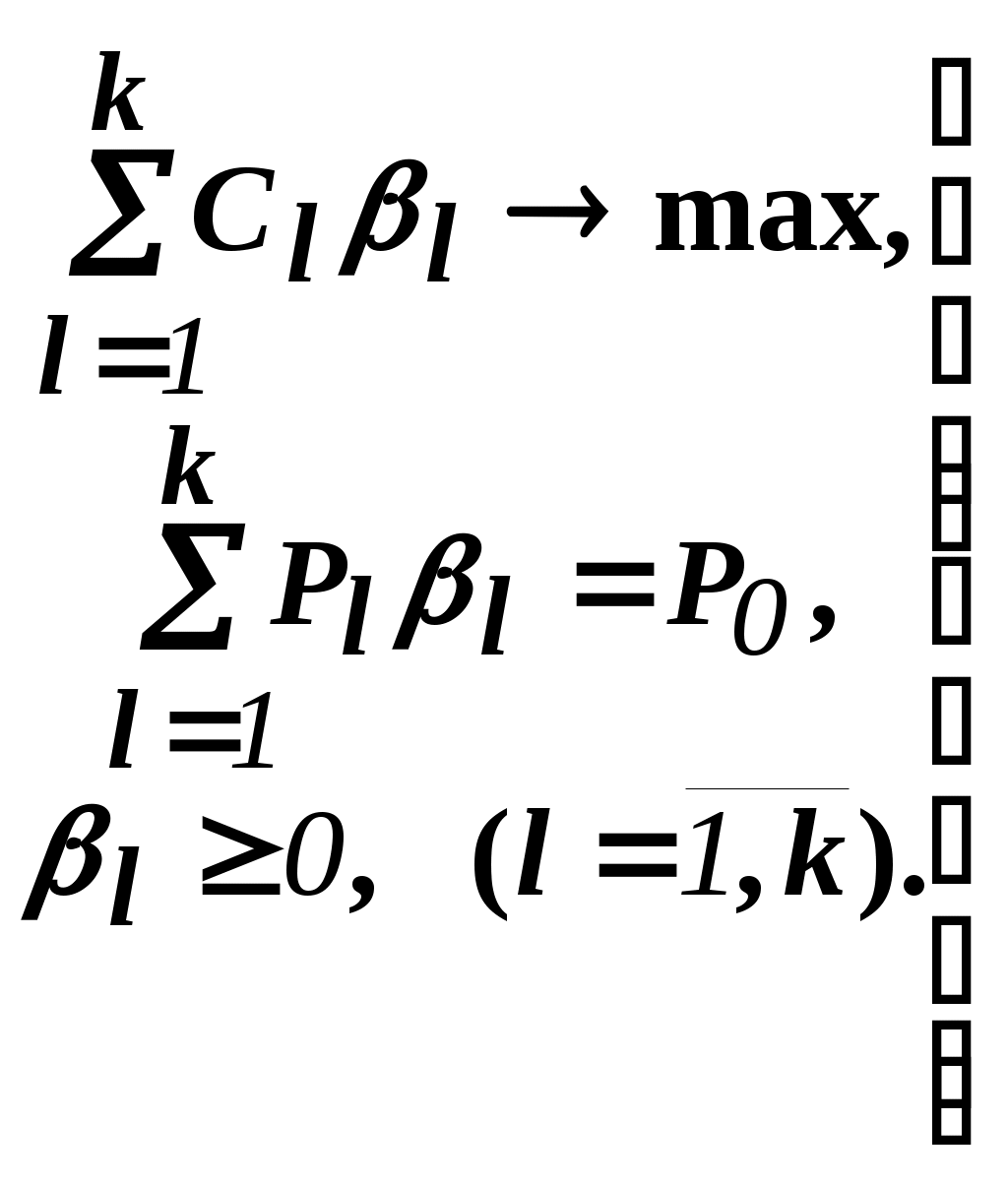 Здесь
Здесь 
Пусть:
B - базисная матрица некоторого опорного решения этой задачи;
B-1 - обратная матрица;
В соответствии с вычислительной схемой модифицированного симплекс-метода4 (МСМ) текущее решение является оптимальным, если для всех небазисных векторов
-
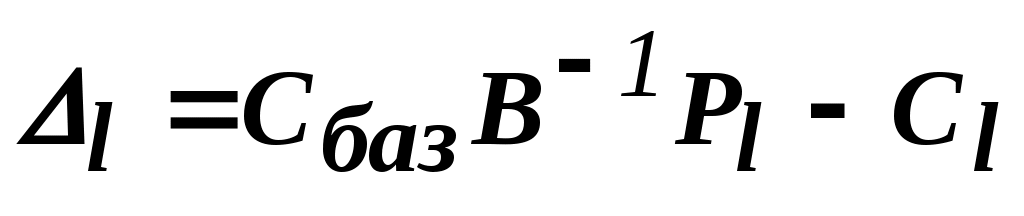 =
=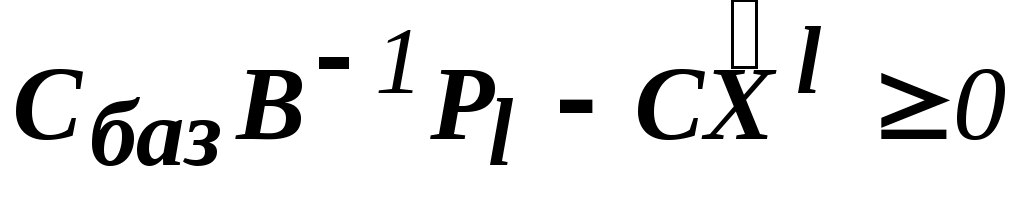 .
.
Начнем анализ этого выражения на предмет исследования возможности его практического использования.
Прежде всего "разберемся" с произведением
-
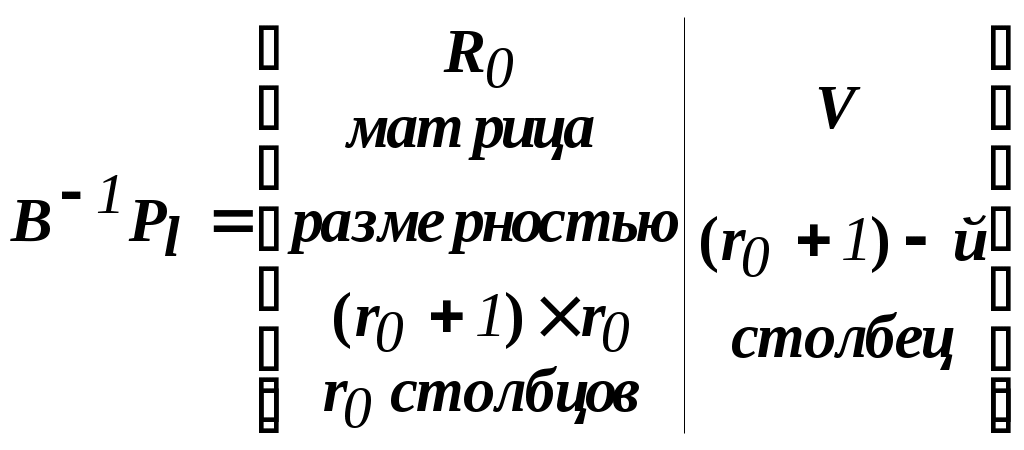
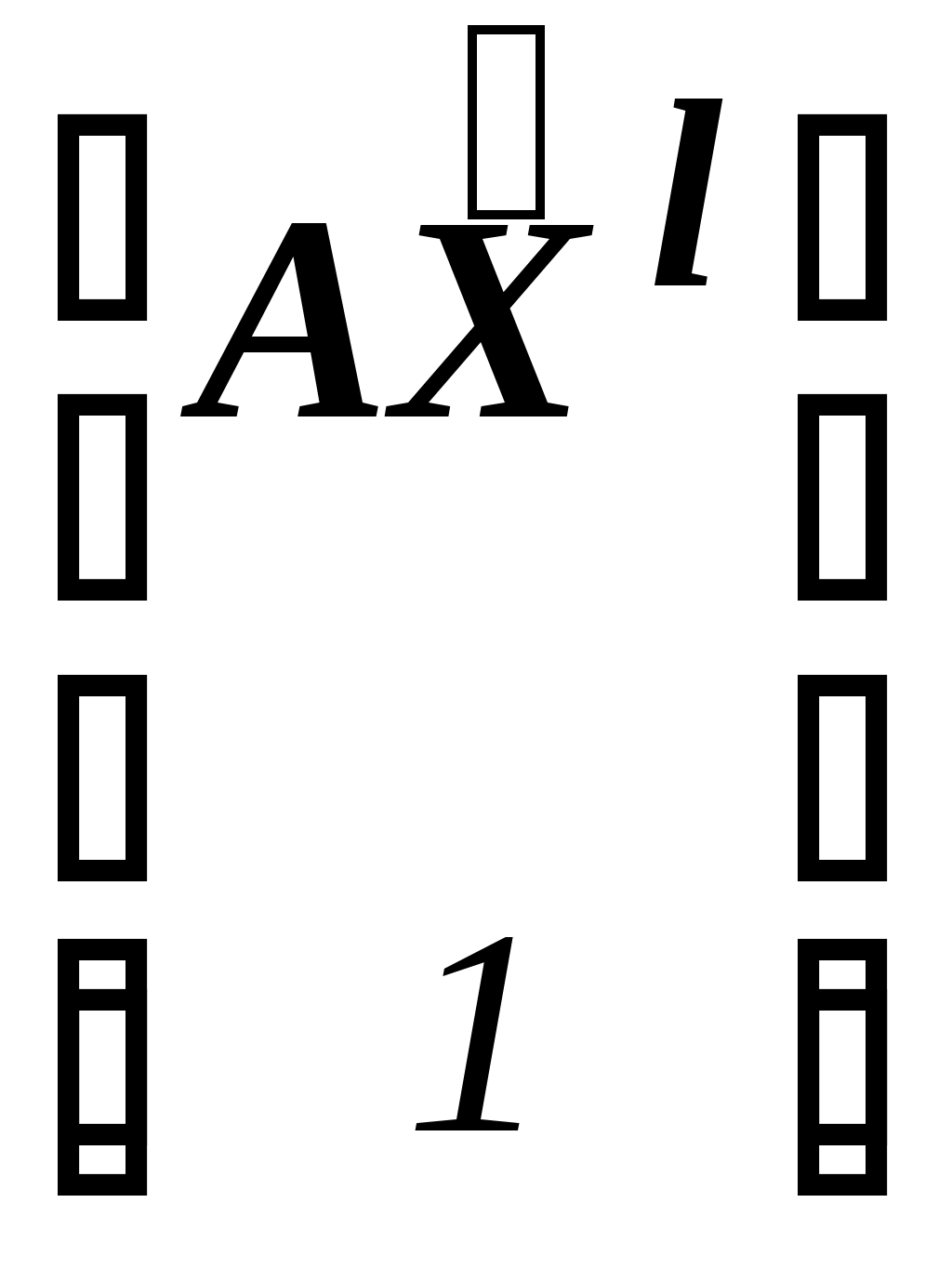 =
=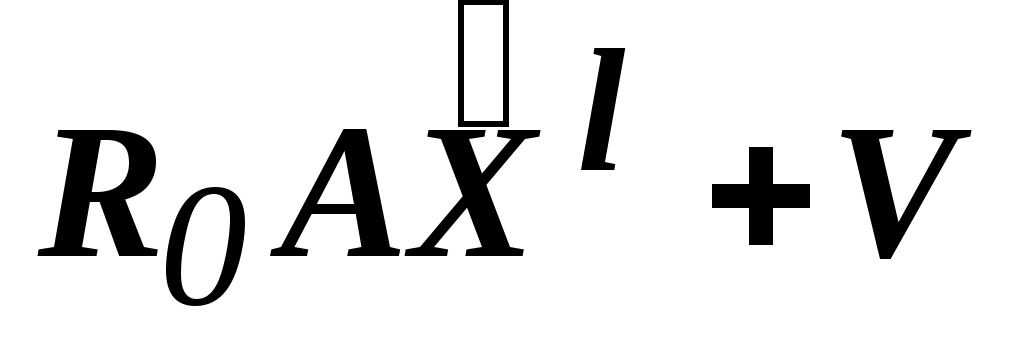 .
.
Подставим (2) в (1):
или
(3)
Самое интересное начинается здесь!
Известно, что если решение не оптимальное, вектор Pl , которому соответствует отрицательная оценка (желательно, максимальная по абсолютной величине), должен быть включен в состав базисных векторов.
Проблема же в том, что
.
В свою очередь, численное определение этих элементов невозможно до тех пор, пока не известна соответствующая экстремальная точка
То есть, нужно сначала определить эту экстремальную точку. А как ее определить, если мы знаем только обратную матрицу главной задачи B-1 и Сбаз. Сама же задача задана неявно. Ее просто нет!
Идея метода Данцига - Вулфа заключается в том, чтобы заменить поиск отрицательной оценки путем последовательного перебора свободных векторов текущего опорного решения направленным поиском только одной экстремальной точки, которой соответствует минимальная оценка связанного с этой точкой вектора главной задачи.
Если окажется, что найденная таким образом минимальная оценка неотрицательна, задача решена. Точнее, решена главная задача, а следовательно - и исходная.
В противном случае ясно, какой вектор следует вводить в базис: этот вектор будет полностью определен координатами найденной экстремальной точки.
Итак, нужно найти экстремальную точку, которой соответствует вектор главной задачи, имеющий минимальную оценку.
Это можно сделать, решив следующую задачу:
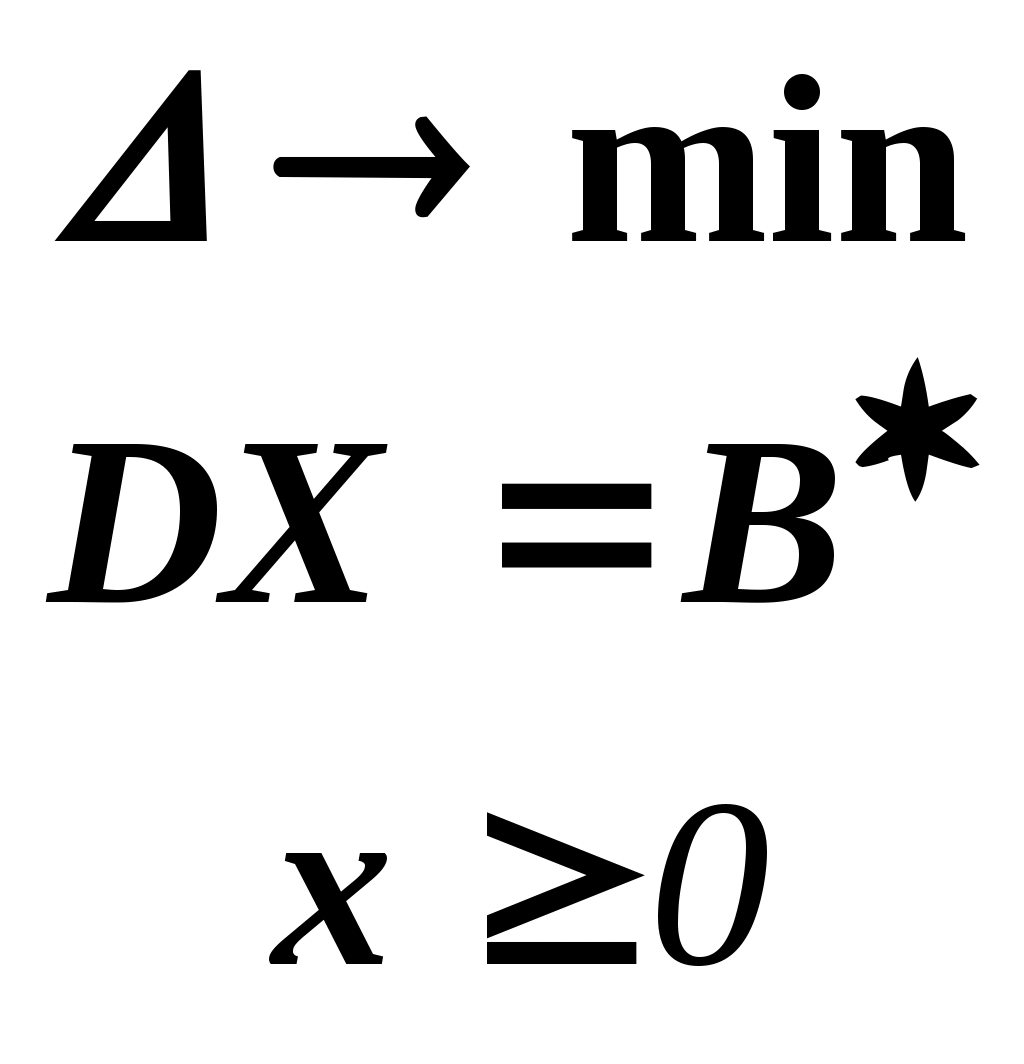
Здесь следует обратить внимание на то, что индекс номера вершины отсутствует. Этот индекс просто неизвестен, т.к. соответствующую вершину еще нужно найти.
В качестве переменных этой задачи выступают координаты искомой вершины.
Мы предположили, что множество, определенное ограничениями
Уже было показано, что:
Теперь, опустив индекс l, имеем:
Ввиду того, что