ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 59
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(5)
Назовем эту задачу частной (или локальной).
Допустим, мы решили эту задачу6 и z* - оптимальное значение ЦФ. Отсюда узнаем и минимальную оценку:
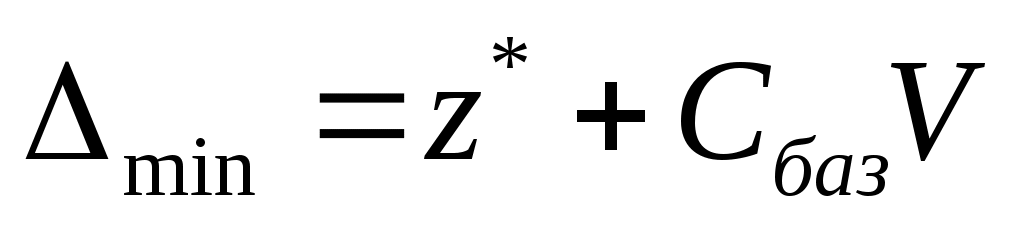
и, что самое главное, и сам свободный вектор, который обладает данной оценкой. Действительно, мы знаем координаты экстремальной точки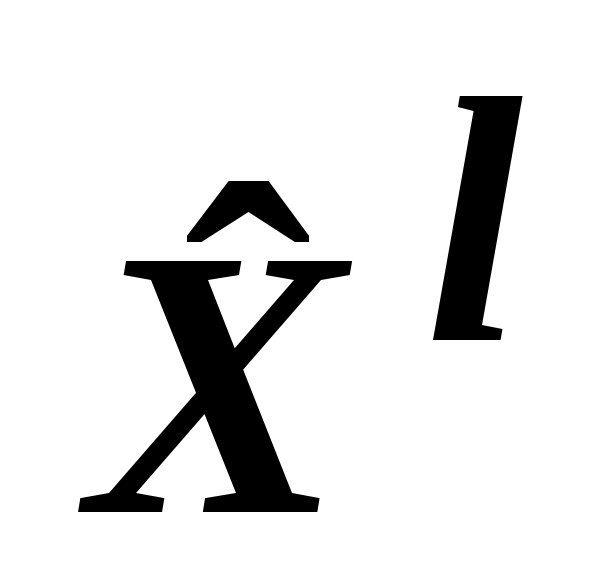 , на которой ЦФ локальной задачи имеет значение z*. Следовательно, можно сформировать вектор главной задачи, соответствующий этой точке:
, на которой ЦФ локальной задачи имеет значение z*. Следовательно, можно сформировать вектор главной задачи, соответствующий этой точке:

Внимание! Здесь l - это не номер вершины, а номер итерации, на которой данная вершина найдена.
Теперь, если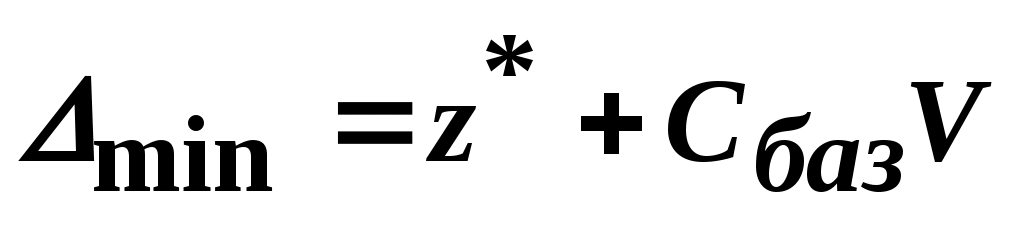 0, то главная задача решена. Исследуемое на текущей итерации решение - оптимальное. Можно восстановить решение исходной задачи. Делается это следующим образом.
0, то главная задача решена. Исследуемое на текущей итерации решение - оптимальное. Можно восстановить решение исходной задачи. Делается это следующим образом.
Пусть *- множество номеров базисных переменных главной задачи.
Тогда, по найденным координатам соответствующих экстремальных точек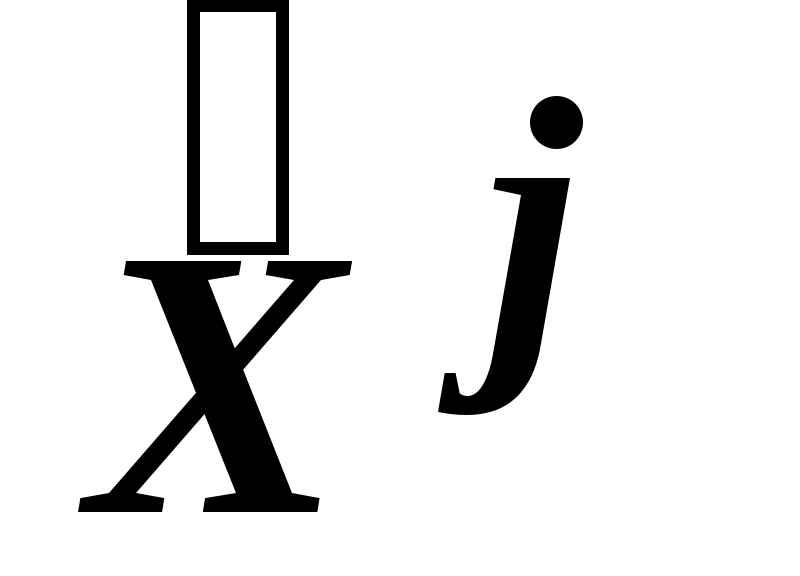 (j*) можно восстановить решение исходной задачи:
(j*) можно восстановить решение исходной задачи:
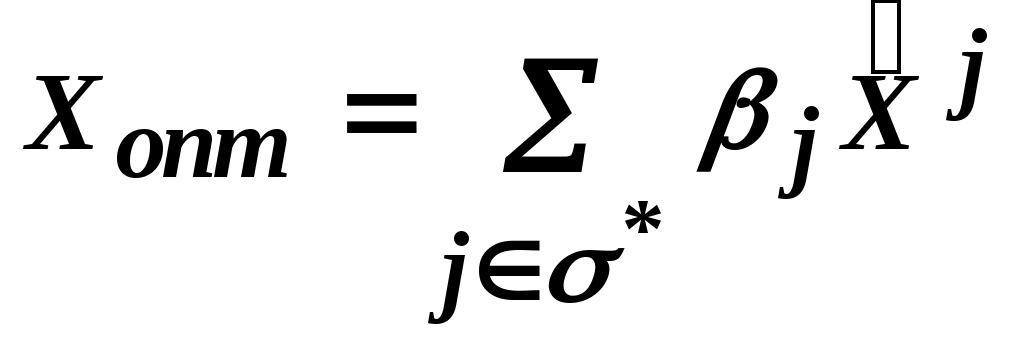
Если , то вектор
, то вектор  нужно ввести в базис нового опорного решения главной задачи. Делается это по правилам МСМ.
нужно ввести в базис нового опорного решения главной задачи. Делается это по правилам МСМ.
На что здесь следует обратить внимание. Мы используем общие принципы обычного симплекс-метода: последовательно переходим от одного опорного решения координирующей задачи к другому, лучшему. Но при каждом таком переходе мы решаем локальную задачу для поиска вектора с минимальной оценкой. При этом, на каждой итерации формируется "своя" ЦФ локальной задачи7.
До сих пор ничего не было сказано о декомпозиции - термине, который фигурирует в названии метода. Более того, мы предположили, что задача имеет один диагональный блок, тем самым, вроде бы "похоронив" саму идею декомпозиции. Это не так.
Дело в том, что при решении каждой локальной задачи:
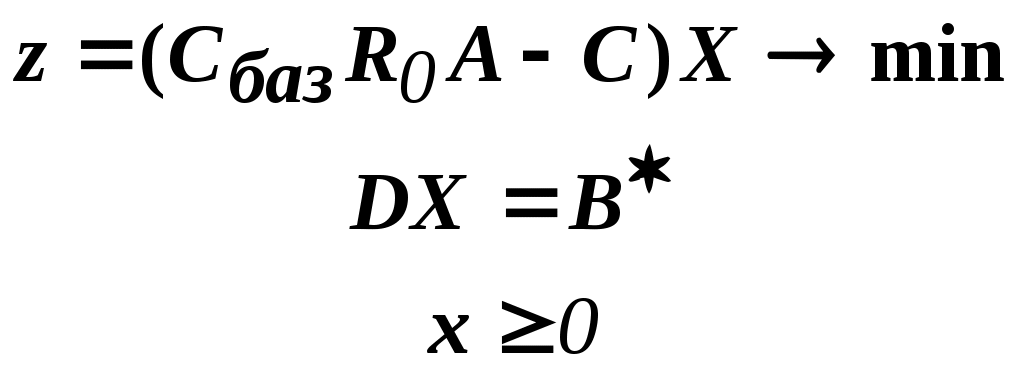
мы сталкиваемся с "чисто" диагональной структурой ее матрицы ограничений (без блока-связки)8.
Дело в том, что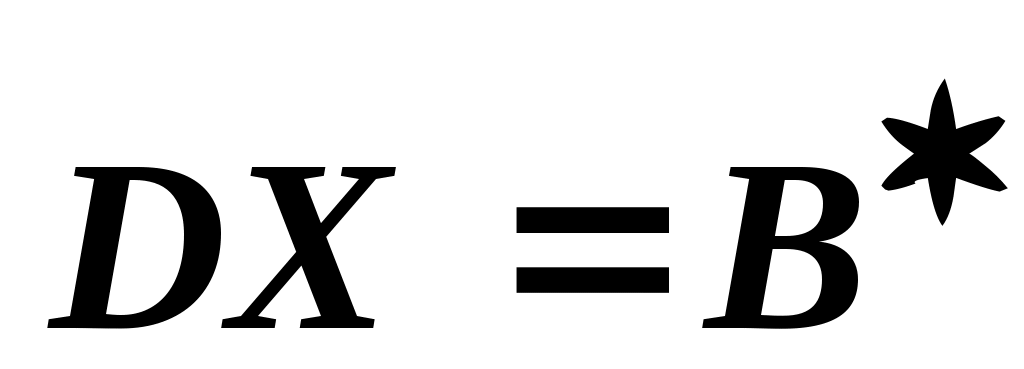 - это сокращенная запись следующей системы ограничений:
- это сокращенная запись следующей системы ограничений:
 =
= ,
,
 =
= ,
,
............................................................................................
 =
= ,
,
............................................................................................
 =
= ,
,
Такая структура допускает простое "разрезание" задачи на Lподзадач меньшей размерности. "Сборка" же решения осуществляется следующим образом.
Пусть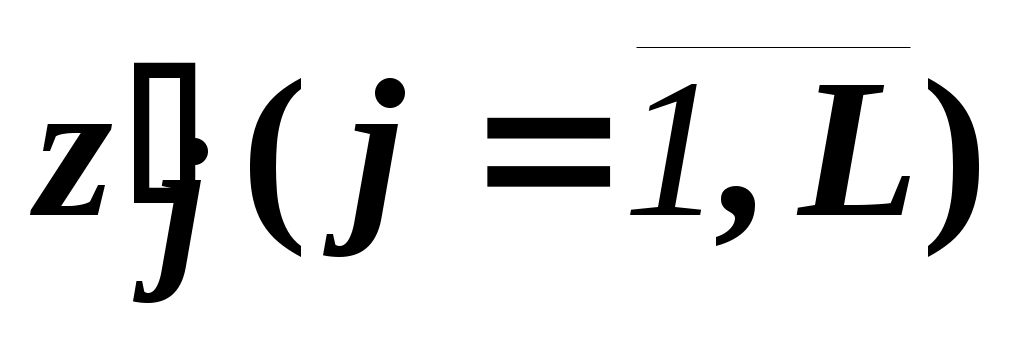 - оптимальное значение ЦФ j-й подзадачи, а
- оптимальное значение ЦФ j-й подзадачи, а 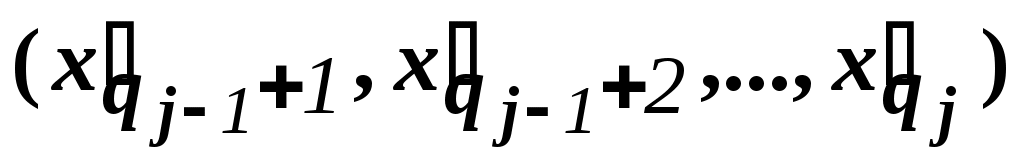 - ее оптимальное решение.
- ее оптимальное решение.
Тогда оптимальное решение локальной задачи определяется:
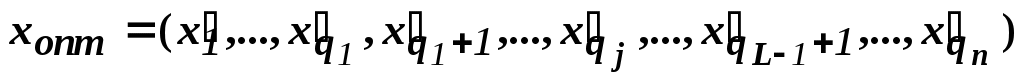 ,
,
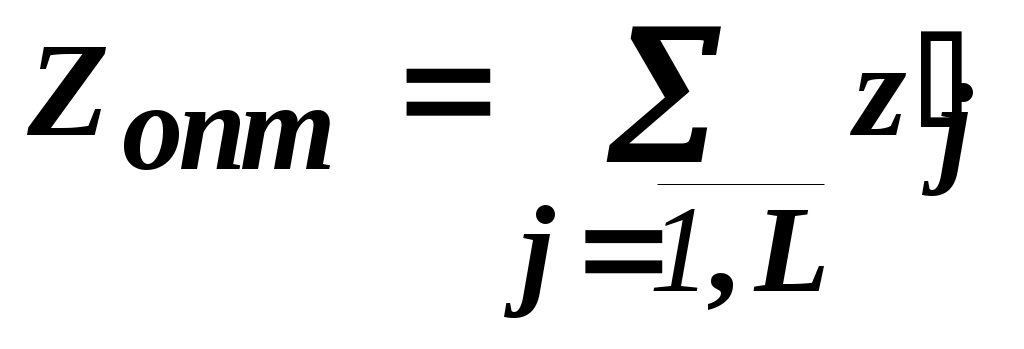 .
.
Дана задача ЛП, ограничения которой составляют блок-связку и ряд диагональных блоков.
При решении координирующей задачи будем считать, что имеем один диагональный блок. При решении же частных задач этот блок будет "распадаться" на соответствующие диагональные блоки.
Т.е. задача имеет вид:
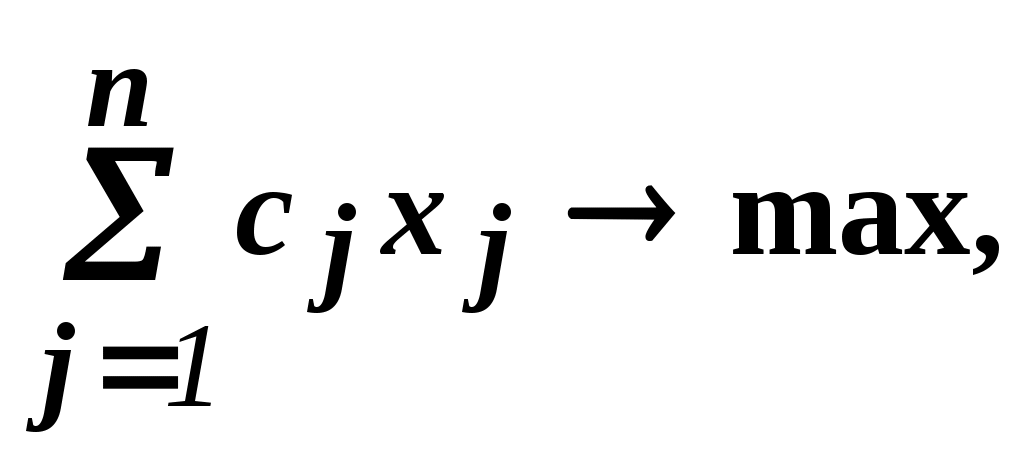

- сохраняем предположение, что допустимое множество задачи не пусто и ЦФ на нем ограничена сверху.
Шаг 1. "Построить" координирующую задачу. Конечно же, - условно: мы не в состоянии этого сделать. Однако, структуру этой задачи мы можем представить следующим образом:
(1)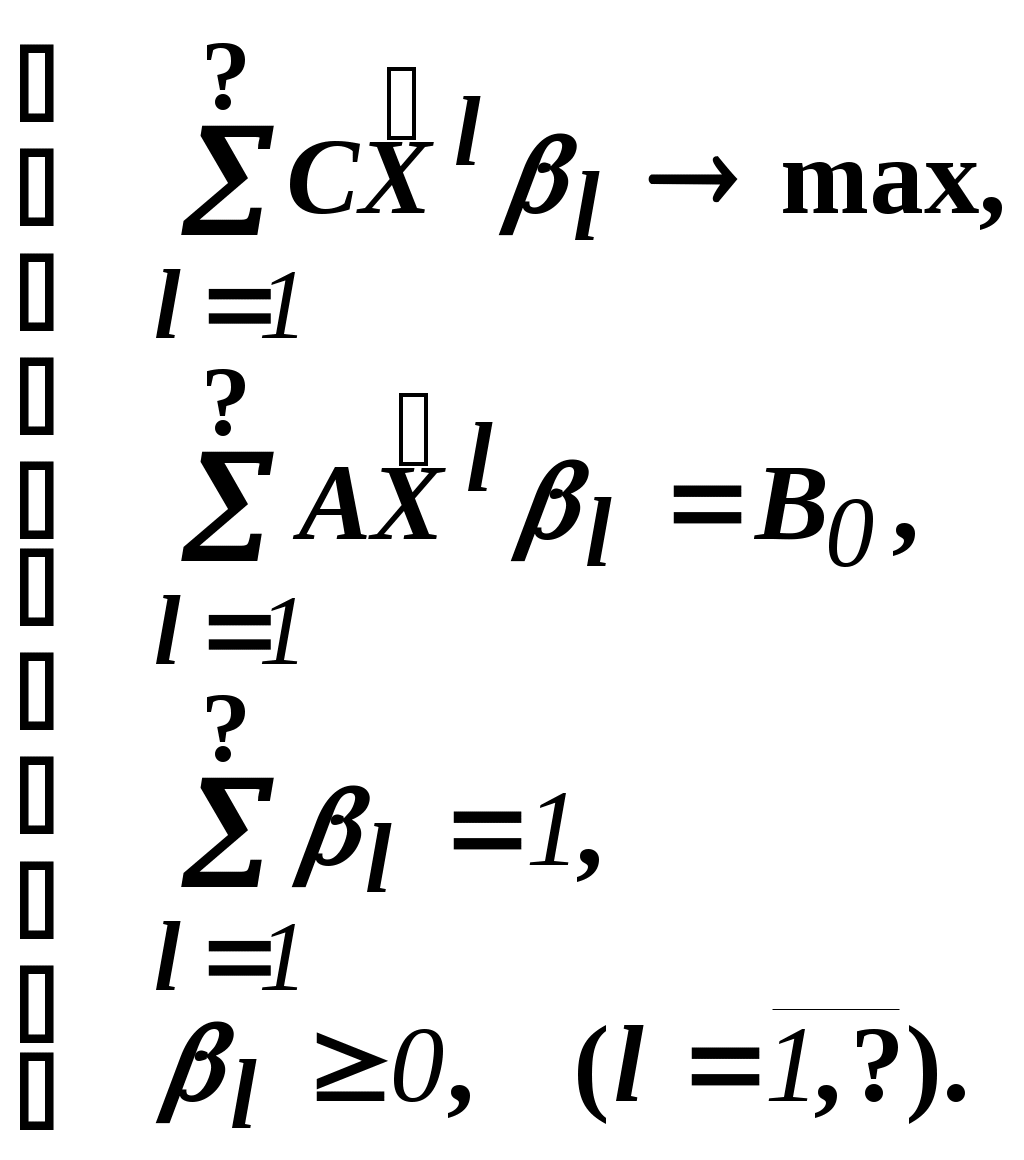
Замечание. Условность этой записи связана еще с одним обстоятельством. Дело в том, что в исходной формулировке ограничения задачи могут быть представлены и уравнениями-ограничениями и нестрогими неравенствами любого направления. Работа же по методу декомпозиции начинается с известного опорного решения координирующей задачи, имеющего, как правило, единичный базис. Для того, чтобы получить такое решение, при сведении координирующей задачи к каноническому виду (с полным набором единичных векторов) в нее вводятся дополнительные и/или искусственные переменные. Это привносит некоторую специфику при реализации метода декомпозиции. При этом координирующую задачу схематически можно представить так:

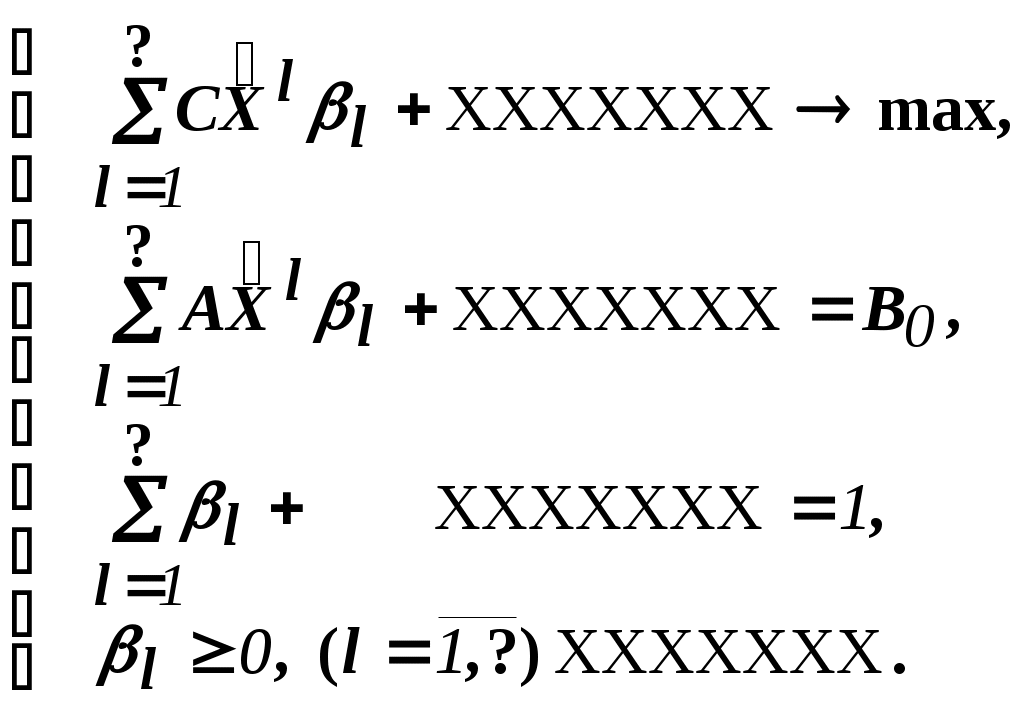
"Область" системы ограничений, по которой строится исходное опорное решение.
Переменные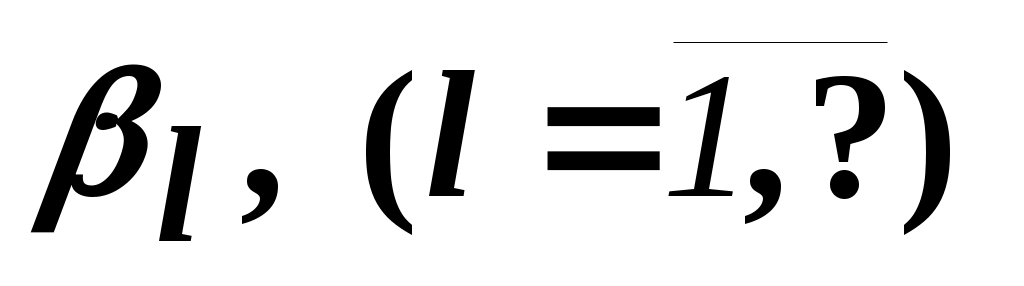 будем называть основными переменными задачи. Все остальные - дополнительные и/или искусственные - вспомогательными.
будем называть основными переменными задачи. Все остальные - дополнительные и/или искусственные - вспомогательными.
Шаг 2. Найти исходное опорное решение координирующей задачи. Обычно для этого используется метод М-задачи: в выделенной области ограничений соответствующие векторы составляют полный единичный базис. Самое интересное, что теперь методом декомпозиции будет решаться координирующая задача, имеющая вид М-задачи! То есть, исходное опорное решение, а также некоторые промежуточные решения будут содержать искусственные переменные в составе базисных.
Замечание.
Для каждого опорного решения координирующей задачи необходимо будет запоминать не только значения базисных переменных, но и координаты вершин, связанных с основными переменными , если эти переменные входят в состав базисных. Проблема в том, что номеров у этих номеров переменных просто нет и быть не может. Поэтому при обозначении этих переменных будем указывать номер итерации, на которой соответствующая переменная вошла в базис.
Чисто технически, мы будем использовать следующий прием.
Допустим имеется базис некоторого опорного решения:
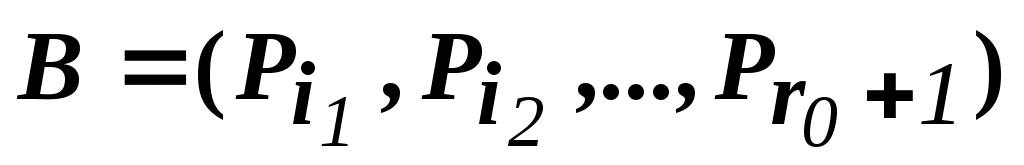 , где
, где
r0+1 - количество ограничений-уравнений в координирующей задаче.
Как уже отмечалось, среди базисных векторов могут быть как основные, так и вспомогательные.
Опорному решению поставим в соответствие массив из r0+1 элементов: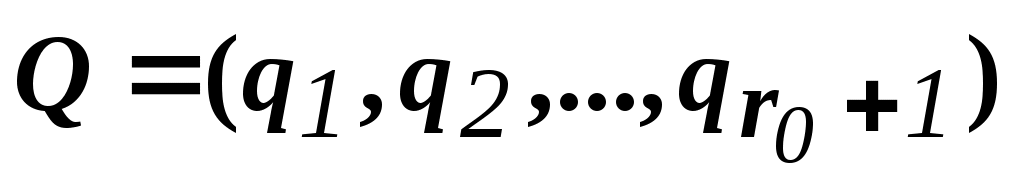 таких, что:
таких, что:

Здесь 0=(0,0,...,0)- n-мерный вектор.
Итак, имеем: опорное решение,
B - базисная матрица опорного решения;
B-1 - обратная матрица;
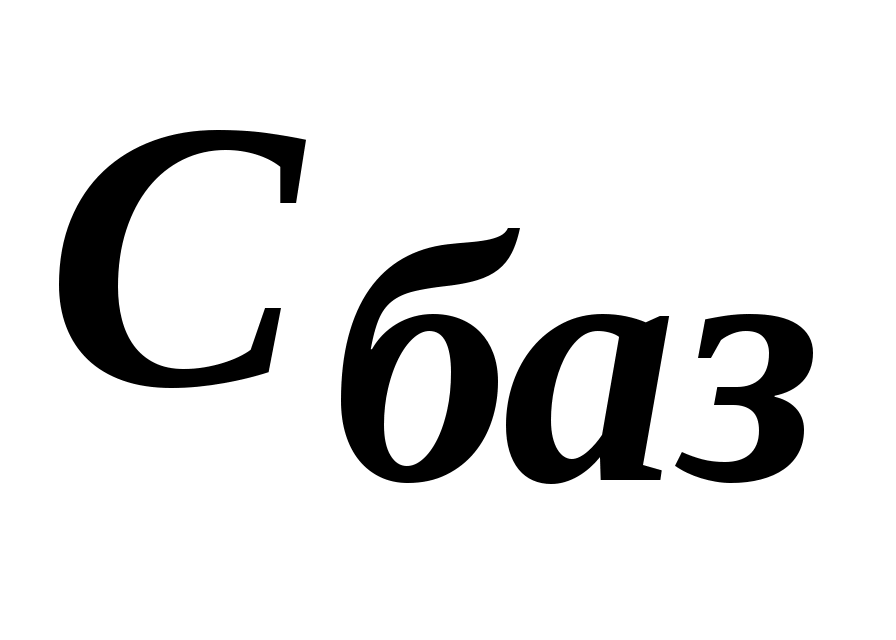 - вектор коэффициентов ЦФ при базисных переменных.
- вектор коэффициентов ЦФ при базисных переменных.
Вычисляем X(P0)=B-1P0 и элементы массива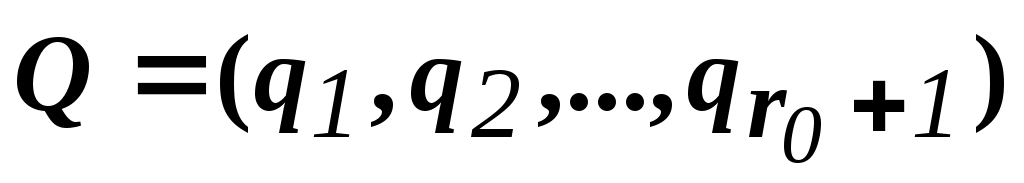
. Заметим, что для исходного опорного решения все элементы этого массива - нулевые, т.к. мы еще не знаем ни одной вершины и базисная матрица состоит из одних вспомогательных векторов.
Полагаем l=1 (номер первой итерации).
шаг 3 Формируем частную задачу:
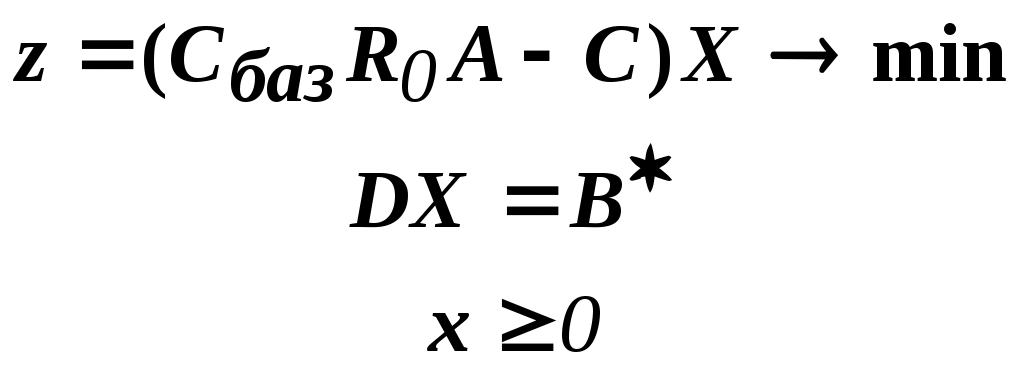
Решаем эту задачу (если D имеет блочно-диагональную структуру, эта задача "распадается" на подзадачи). Собираем решение.
z* - оптимальное значение ЦФ;
 - вектор координат экстремальной точки.
- вектор координат экстремальной точки.
Вычисляем оценку: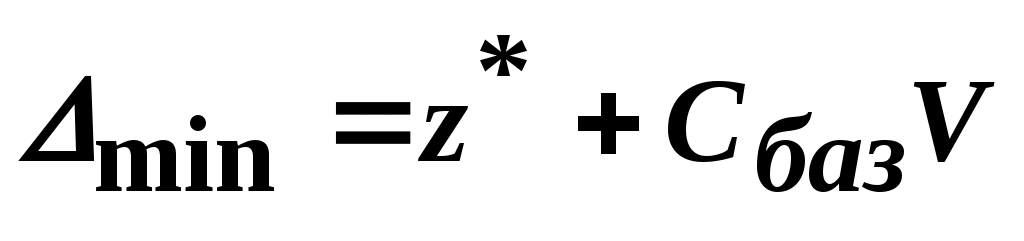 =
=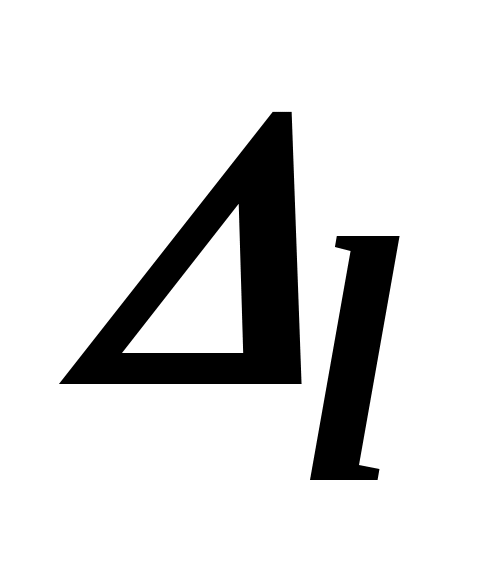 .
.
Если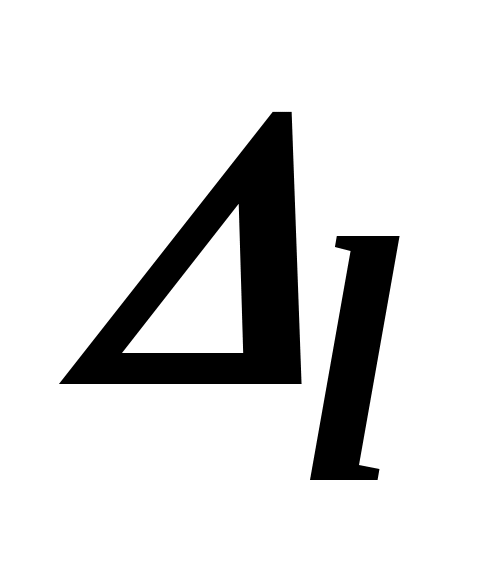 0 , переходим к шагу 6. В противном случае выполняем следующий шаг.
0 , переходим к шагу 6. В противном случае выполняем следующий шаг.
шаг 4. Находим вектор Pl , которому соответствует найденная отрицательная оценка:
 .
.
шаг 5.
X(Pl)=B-1Pl .
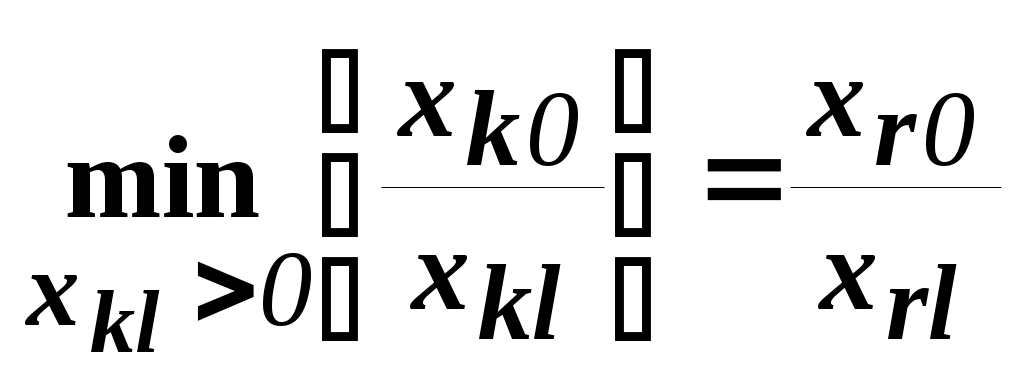
Назовем эту задачу частной (или локальной).
Допустим, мы решили эту задачу6 и z* - оптимальное значение ЦФ. Отсюда узнаем и минимальную оценку:
и, что самое главное, и сам свободный вектор, который обладает данной оценкой. Действительно, мы знаем координаты экстремальной точки
Внимание! Здесь l - это не номер вершины, а номер итерации, на которой данная вершина найдена.
Теперь, если
Пусть *- множество номеров базисных переменных главной задачи.
Тогда, по найденным координатам соответствующих экстремальных точек
Если
На что здесь следует обратить внимание. Мы используем общие принципы обычного симплекс-метода: последовательно переходим от одного опорного решения координирующей задачи к другому, лучшему. Но при каждом таком переходе мы решаем локальную задачу для поиска вектора с минимальной оценкой. При этом, на каждой итерации формируется "своя" ЦФ локальной задачи7.
Декомпозиция в методе Данцига-Вулфа
До сих пор ничего не было сказано о декомпозиции - термине, который фигурирует в названии метода. Более того, мы предположили, что задача имеет один диагональный блок, тем самым, вроде бы "похоронив" саму идею декомпозиции. Это не так.
Дело в том, что при решении каждой локальной задачи:
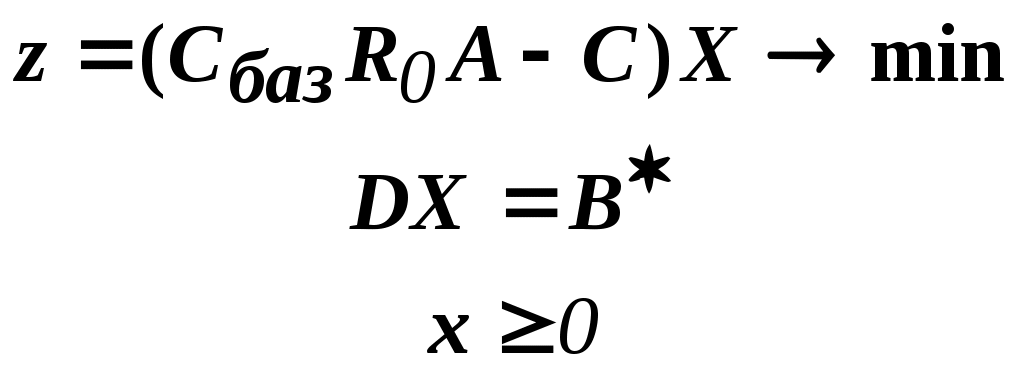
мы сталкиваемся с "чисто" диагональной структурой ее матрицы ограничений (без блока-связки)8.
Дело в том, что
............................................................................................
............................................................................................
Такая структура допускает простое "разрезание" задачи на Lподзадач меньшей размерности. "Сборка" же решения осуществляется следующим образом.
Пусть
Тогда оптимальное решение локальной задачи определяется:
Алгоритм метода декомпозиции
Дана задача ЛП, ограничения которой составляют блок-связку и ряд диагональных блоков.
При решении координирующей задачи будем считать, что имеем один диагональный блок. При решении же частных задач этот блок будет "распадаться" на соответствующие диагональные блоки.
Т.е. задача имеет вид:

- сохраняем предположение, что допустимое множество задачи не пусто и ЦФ на нем ограничена сверху.
Шаг 1. "Построить" координирующую задачу. Конечно же, - условно: мы не в состоянии этого сделать. Однако, структуру этой задачи мы можем представить следующим образом:
(1)
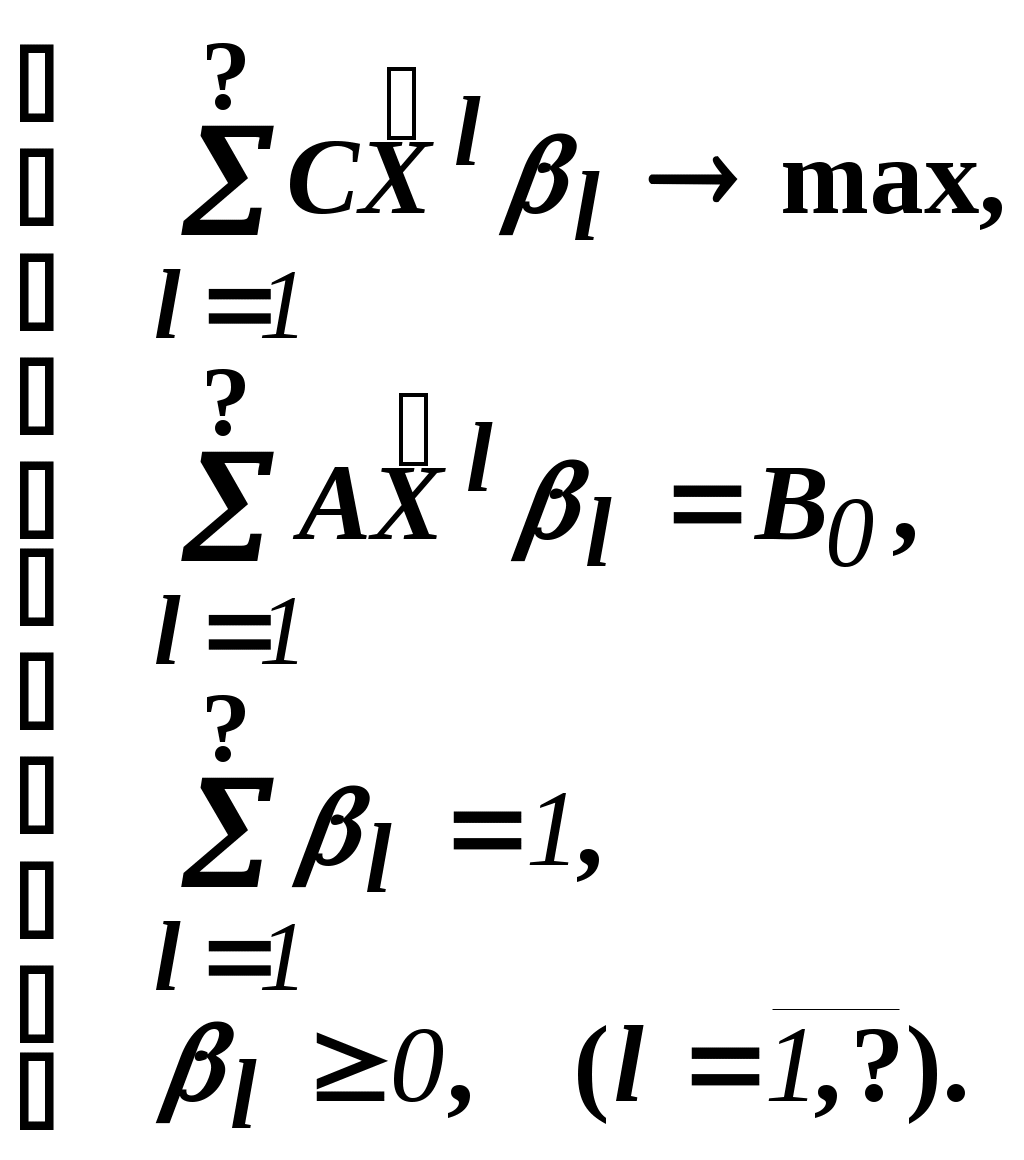
Замечание. Условность этой записи связана еще с одним обстоятельством. Дело в том, что в исходной формулировке ограничения задачи могут быть представлены и уравнениями-ограничениями и нестрогими неравенствами любого направления. Работа же по методу декомпозиции начинается с известного опорного решения координирующей задачи, имеющего, как правило, единичный базис. Для того, чтобы получить такое решение, при сведении координирующей задачи к каноническому виду (с полным набором единичных векторов) в нее вводятся дополнительные и/или искусственные переменные. Это привносит некоторую специфику при реализации метода декомпозиции. При этом координирующую задачу схематически можно представить так:

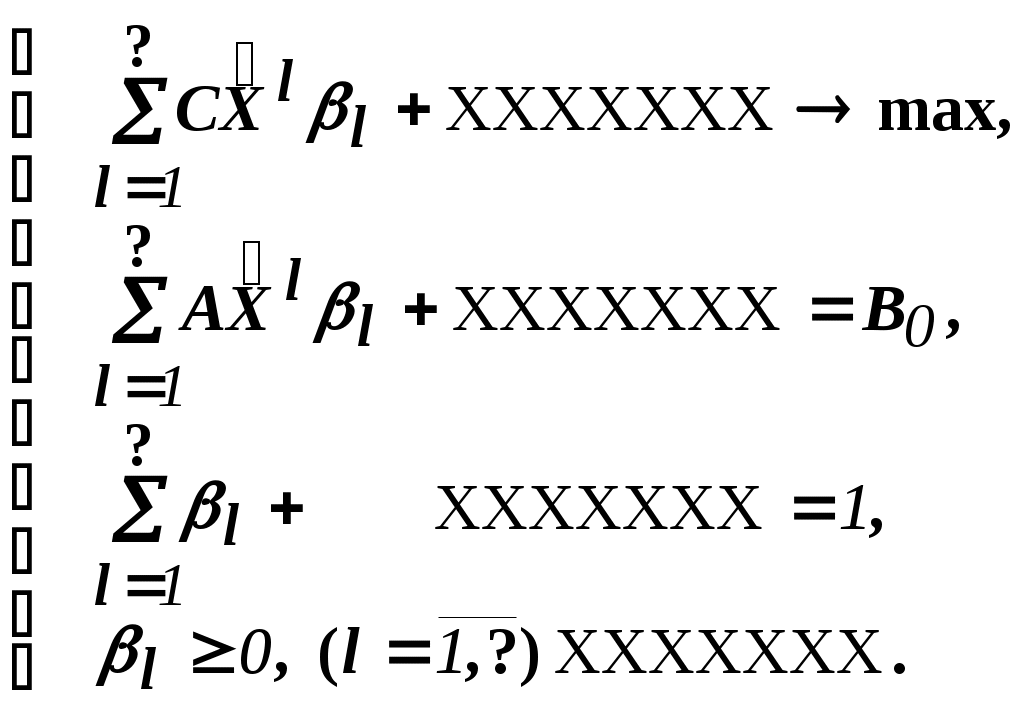
"Область" системы ограничений, по которой строится исходное опорное решение.
Переменные
Шаг 2. Найти исходное опорное решение координирующей задачи. Обычно для этого используется метод М-задачи: в выделенной области ограничений соответствующие векторы составляют полный единичный базис. Самое интересное, что теперь методом декомпозиции будет решаться координирующая задача, имеющая вид М-задачи! То есть, исходное опорное решение, а также некоторые промежуточные решения будут содержать искусственные переменные в составе базисных.
Замечание.
Для каждого опорного решения координирующей задачи необходимо будет запоминать не только значения базисных переменных, но и координаты вершин, связанных с основными переменными , если эти переменные входят в состав базисных. Проблема в том, что номеров у этих номеров переменных просто нет и быть не может. Поэтому при обозначении этих переменных будем указывать номер итерации, на которой соответствующая переменная вошла в базис.
Чисто технически, мы будем использовать следующий прием.
Допустим имеется базис некоторого опорного решения:
r0+1 - количество ограничений-уравнений в координирующей задаче.
Как уже отмечалось, среди базисных векторов могут быть как основные, так и вспомогательные.
Опорному решению поставим в соответствие массив из r0+1 элементов:

| БАЗ. | Q | |||
| | 1 | 2 | ... | n |
| | | |||
| | | |||
| | ||||
| | | |||
| | ||||
| | | |||
Здесь 0=(0,0,...,0)- n-мерный вектор.
Итак, имеем: опорное решение,
B - базисная матрица опорного решения;
B-1 - обратная матрица;
Вычисляем X(P0)=B-1P0 и элементы массива
. Заметим, что для исходного опорного решения все элементы этого массива - нулевые, т.к. мы еще не знаем ни одной вершины и базисная матрица состоит из одних вспомогательных векторов.
Полагаем l=1 (номер первой итерации).
шаг 3 Формируем частную задачу:
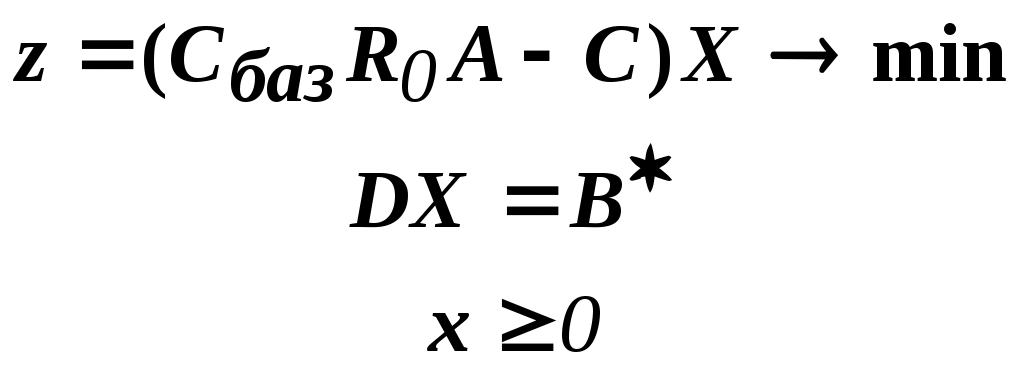
Решаем эту задачу (если D имеет блочно-диагональную структуру, эта задача "распадается" на подзадачи). Собираем решение.
z* - оптимальное значение ЦФ;
Вычисляем оценку:
Если
шаг 4. Находим вектор Pl , которому соответствует найденная отрицательная оценка:
шаг 5.
-
Ищем разложение этого вектора:
X(Pl)=B-1Pl .
-
По обычному для симплекс-метода правилу находим вектор, который нужно вывести из базиса:
-
Корректируем вектор . Если вводимый вектор - основной, принимаем
. Если вводимый вектор - основной, принимаем 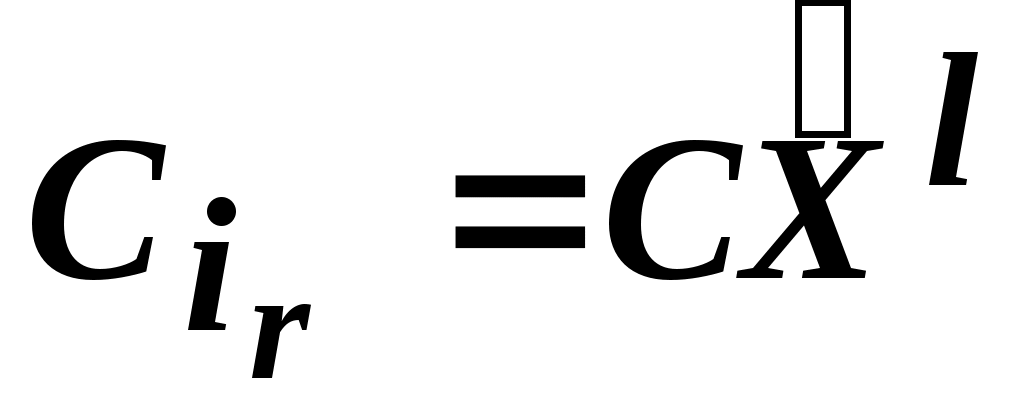 .
. -
Корректируем массив : r-му элементу
: r-му элементу 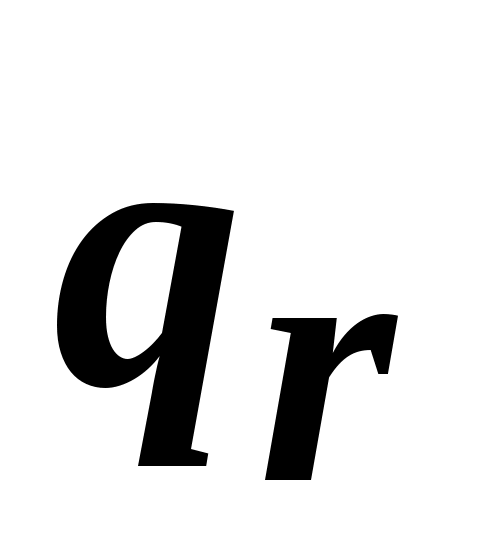 ставим в соответствие вектор координат найденной вершины
ставим в соответствие вектор координат найденной вершины  или (0,0,...,0) в зависимости от того, является ли вводимая в состав базисных переменная основной или вспомогательной.
или (0,0,...,0) в зависимости от того, является ли вводимая в состав базисных переменная основной или вспомогательной. -
Формируем новую обратную матрицу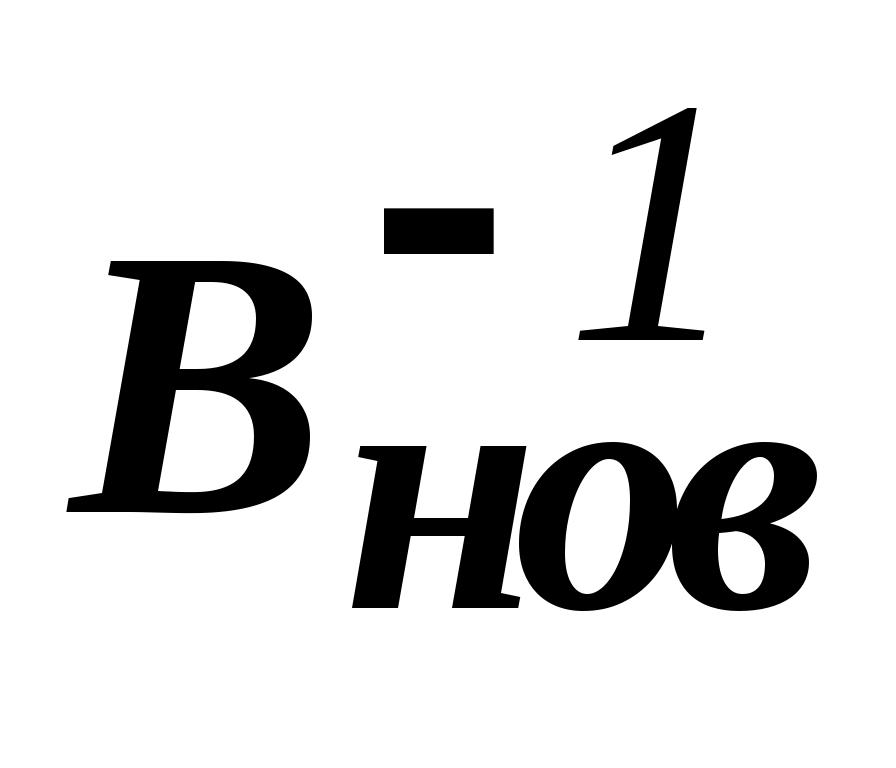 (известно разложение вектора Pl по старому базису, известен ведущий элемент):
(известно разложение вектора Pl по старому базису, известен ведущий элемент):