ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 55
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=
, где 
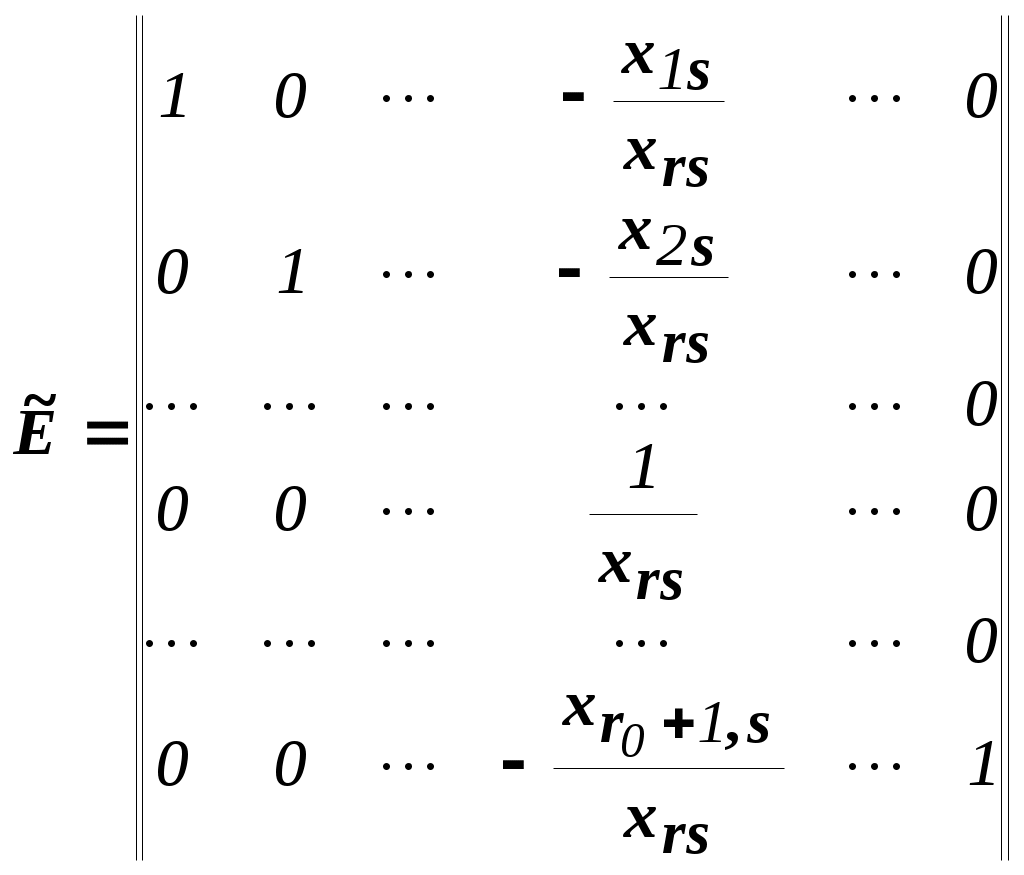- "почти единичная матрица-
Находим новое разложение вектора P0 по базису:
X(P0)=
P0 .-
Положив l=l+1, переходим к шагу 3.
шаг 6. Все оценки у основных векторов неотрицательны. Необходимо проверить оценки вспомогательных векторов.
Вычисление этих оценок проводим по обычным правилам:
.Если обнаруживается вспомогательный вектор с отрицательной оценкой (As) , переходим к шагу 5. При этом, в качестве Pl принимаем As . В противном случае выполняем следующий шаг.
Шаг 7. Получено оптимальное решение координирующей задачи:
- значения базисных переменных.Известен массив
. Восстанавливается решение исходной задачи:
. Это соответствует 
. Конец.1 В этой связи следует отметить, что важнейшая составляющая процесса решения произвольной задачи нелинейного программирования - это анализ задачи на предмет определения возможности использования той или иной группы методов (например, выпуклый анализ)
2 Непосредственно о декомпозиции речь пока не идет.
3 Достаточно представить (мысленно), что эта задача ЕСТЬ(есть не в памяти ЭВМ, а вообще есть!).
4 Почему МСМ? Дело в том, что именно в рамках схемы МСМ можно не знать коэффициентов разложения тех векторов, чьи оценки нужно вычислить.
5
-это вектор коэффициентов разложения вектора 
по базису.6 Другого, в предположении, что допустимое множество ограничено, не может быть.
7 Коэффициенты ЦФ локальной задачи определяются через обратную матрицу очередного опорного решения главной задачи.
8 Вспомним задачу, помеченную большим восклицательным знаком.