Задание 5.13.Найти корни кубического уравнения (полинома)с одним неизвестным 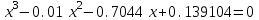с помощью средства Подбор параметра.

Выполнение.

Сначала находим интервалы, на которых существуют корни полинома. Такими интервалами, являются промежутки, на концах которых функция меняет знак. С этой целью построим таблицу значений полинома на интервале (-1,1) с шагом 0.2 и построим график. Для этого:

1. Введем в ячейку A2 значение –1 , а в A3 – значение: – 0.8.

2. Используя маркер заполнения, заполним ячейки до А12.

3. В ячейку B2 вводим формулу: = A2^3 – 0,01*A2^2 – 0,7044*A2 + 0,139104.

4. Заполняем диапазон B3:B12.

5. По полученным значениям строим график заданного полинома.



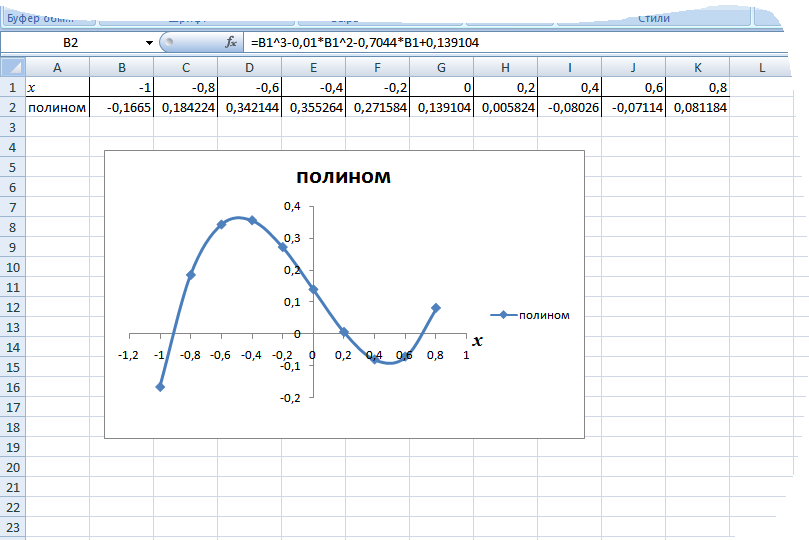
Мы увидим, что для нашего случая полином меняет знакна интервалах [-1,-0.8], [0.2, 0.4] и [0.6, 0.8],т.е. пересекается с осью x.Интервалов три – столько корней имеет уравнение третьей степени. Корни локализованы.

Теперь зададим точность нахождения значений корней. На вкладке Office → Параметры Excel → Формулы → Параметры вычислений задаем относительную погрешность 0,00001 и предельное число итераций 1000 (число последовательных приближений).

Отводим на новом рабочем листе ячейку С2под первый корень, соответственноячейки C3 и C4 под второй и третий корниполинома.

Корни будем находим методом последовательных приближений. Поэтому в ячейку С2 вводим сначала значение, являющееся первым приближением к искомому корню. В нашем случае возьмем первый отрезок и в нем среднее значение, т.е. – 0,9. Соответственно в ячейки С3 и С4 вводим приближенные значения для второго и третьего корней: +0,3 и +0,7.

Для нахождения корня с помощью Подбора параметра уравнение надо представить в таком виде, чтобы его правая часть не содержала переменную. В нашем примере этого не требуется. Отводим ячейку D2под функцию, для которой ведется поиск первого корня. Причем вместо неизвестной x у этой функции должна указываться ссылка на ячейку, отведенную под искомый корень. Таким образом, в ячейку D2вводится формула:

= C2^3 – 0,01*C2^2 – 0,7044*C2 + 0.139104.

Копируем эту формулу в ячейки D3 и D4для второго и третьего корнейполинома. С помощью инструмента Подбор параметра

---

находим первый корень:

1. Выбираем команду Данные → Работа с данными→ Анализ «что-если» →Подбор параметра. На экране появится диалоговое окно.



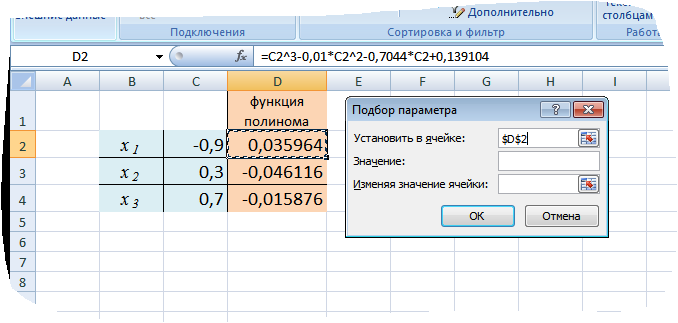
2. В поле Установить в ячейке введем ссылку на ячейку D2, в которой введена формула, вычисляющая значение левой части полинома.

3. В поле Значение вводим 0 – значение из правой части уравнения.

4. В поле Изменяя значение ячейки введем С2 – ссылка на ячейку, отведенную под первый корень.

5. Нажимаем ОК.

Получим окно с результатами:



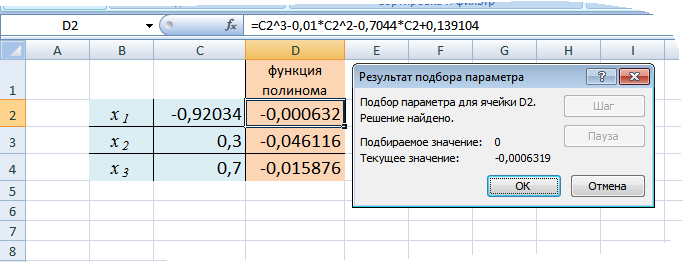
Закрыв окно, найденное приближенное значение корня помещается в ячейку D2. В данном случае оно равно –0,92034.

Аналогично, повторив действия 1–5 для каждого из оставшихся корней, в ячейках D3 и D4 находим их значения. Соответственно, они равны0,21021 и 0,72071.

Содержание отчета

Отчет должен содержать тему, ответы на контрольные вопросы, выполненные задания своего варианта с промежуточными вычислениями.

Контрольные вопросы

1. Что такое Надстройки и где они находятсяв Excel 2007?

2. Для чего используется Пакет анализа?

3. Как подключить пакет Поиск решения?

4. Рассказать о структуре окна Поиск решения.

6. Как выбираются границы интервалов значений х и у при нахождении корней уравнений используя Поиск решения?

7. Как выбрать начальное приближение неизвестных х и у?

8. Почему в окне Поиск решения нужно установить параметр Минимальное значение?

9. Для какой цели вводится Целевая ячейка?

10. Что находят с помощью средства Подбор параметра.

11. Как задать точность вычислений?

12. Как отделить интервалы, в которых находятся корни кубического уравнения, с помощью построения графика?

Варианты заданий

1. Найти корни системы нелинейных уравнений, используя Поиск решений, согласно своему варианту.

Вариант 1.	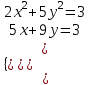Вариант 2.	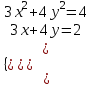Вариант 3.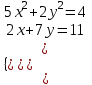
Вариант 4.	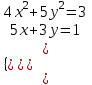Вариант 5.	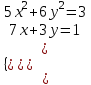Вариант 6.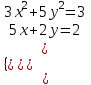
Вариант 7.	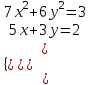Вариант 8.	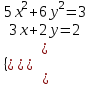Вариант 9.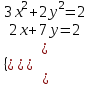
Вариант 10.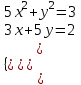

---

2. Найти с помощью инструментаПодбор параметра корни кубического уравнения с одной переменной согласно своему варианту.

Вариант 1.	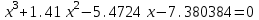Вариант 2.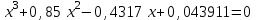
Вариант 3.	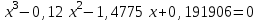Вариант 4.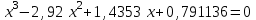
Вариант 5.	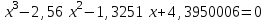Вариант 6.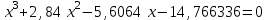
Вариант 7.	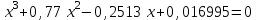Вариант 8.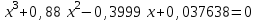
Вариант 9.	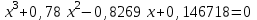Вариант 10.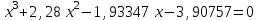

---

Смотрите также файлы

• Тема История возникновения, понятие и виды налогов.docx

• Финансовый учет является учетом Выберите один ответ а инструментальным.pdf

• Министерство науки и образования российской федерации.doc

• Федеральное агентство.docx

• Тема Выпуклые и вогнутые функции. Их основные свойства. Выпуклые и вогнутые функции.doc