ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 229
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Таким образом, получено уравнение параболы с вершиной в начале координат, проходящей через точку А, принадлежащую кривой и имеющую координаты
и имеющую координаты  и
и  .
.
Парабола ОАi – A2 – A1 – A представляет собой геометрическое место точек, определяющих режимы насоса, подобных режиму в точке А, и называется параболой подобных режимов.
Пересчет координат точки А по закону пропорциональности для любой другой частоты вращения приведет к точкам на параболе подобных режимов.
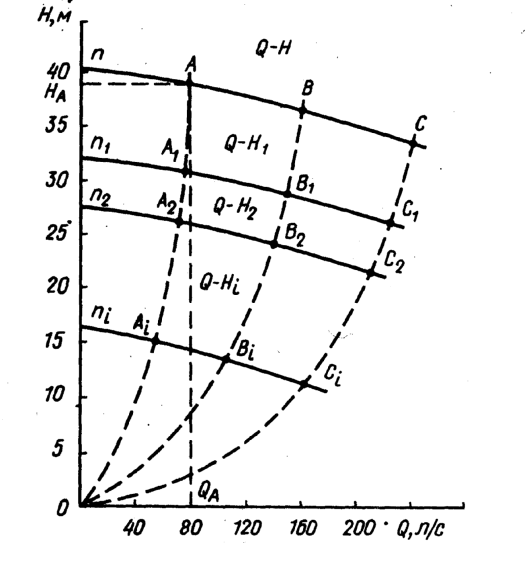
Пересчет всякой другой точки В, С, … характеристики построенной при частоте вращения
построенной при частоте вращения  на частоту
на частоту  ,
,  , …
, …  даст точки
даст точки  ,
,  , …
, … 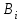 ;
; 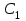 ,
, 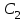 , …
, … 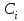 и так далее, которые расположатся соответственно на параболах
и так далее, которые расположатся соответственно на параболах 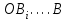 ;
; 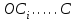 .
.
Соединяя точки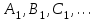 плавной кривой, получаем характеристику
плавной кривой, получаем характеристику 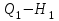 насоса для частоты вращения
насоса для частоты вращения  .
.
Для характеристик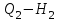 …
… 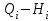 построения будут аналогичными.
построения будут аналогичными.
Теоретически параболы подобных режимов являются линиями постоянного КПД.
В действительности насос не сохраняет постоянство КПД. Это связано с тем, что при изменении частоты вращения в разной степени и с разной интенсивностью проявляются потери мощности насоса (механические, объемные, гидравлические).
Отмечая на полученных характеристиках ,
,  …
…  точки с равными значениями КПД и соединяя их плавными кривыми, получаем так называемую универсальную характеристику.
точки с равными значениями КПД и соединяя их плавными кривыми, получаем так называемую универсальную характеристику.
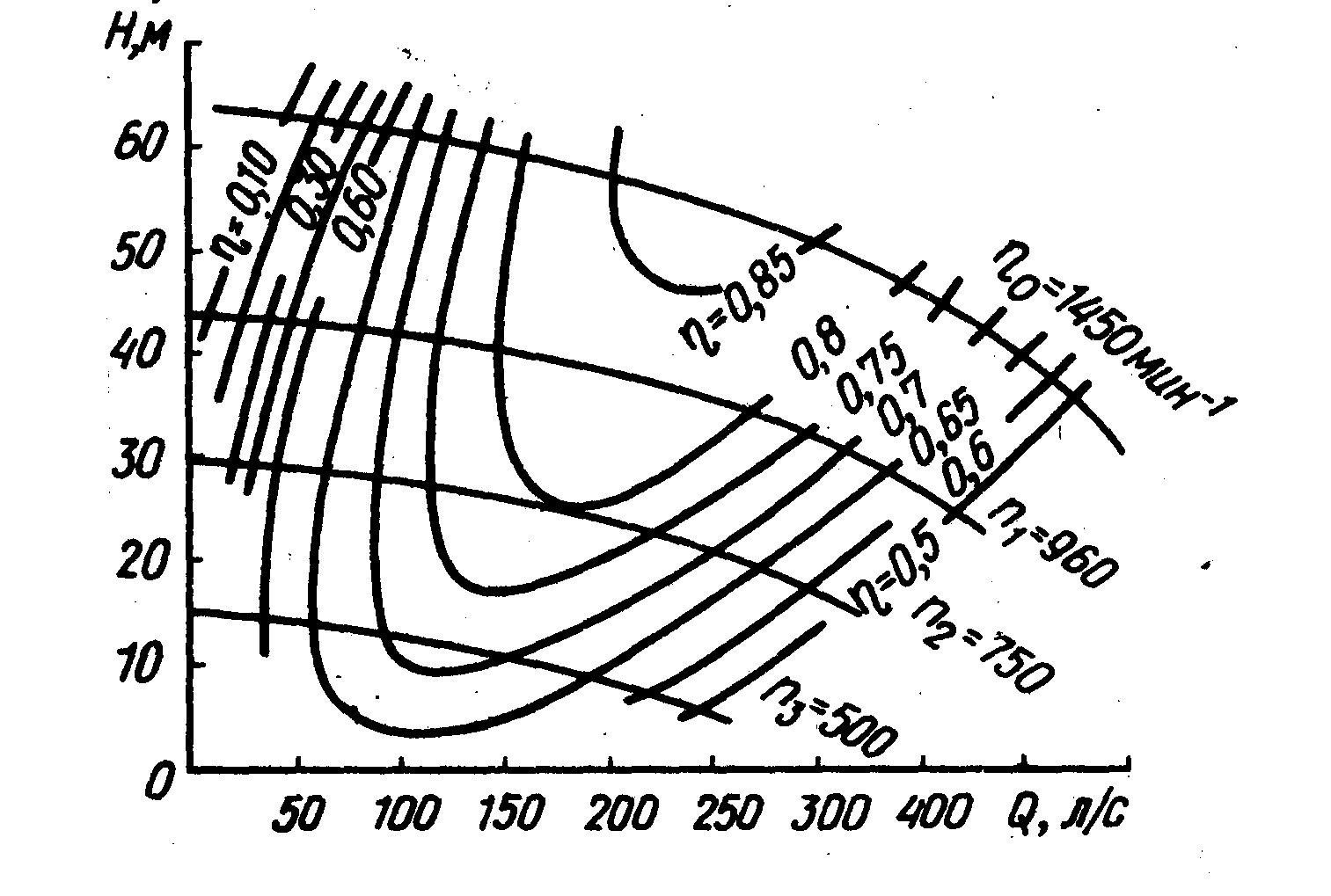
Из которой видно, что максимальное значение КПД обеспечивают двигатели с частотой вращения 1450 мин-1.
Требования потребителей по подаче и напору чрезвычайно разнообразны, поэтому экономически нецелесообразно изготовлять насосы для каждого расчетного случая.
Для увеличения области применения насоса в практике проектирования и эксплуатации насосных станций применяют срезку рабочего колеса насоса, т. е. уменьшают диаметр рабочего колеса по внешнему обводу , сохраняя
, сохраняя 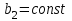 .
.
Подачу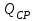 и напор
и напор 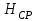 насоса, имеющего срезанное рабочее колесо диаметром
насоса, имеющего срезанное рабочее колесо диаметром 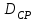 , можно определить по уравнениям закона подобия центробежных насосов:
, можно определить по уравнениям закона подобия центробежных насосов:
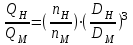 ;
; 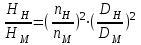 ;
; 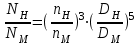 ,
,
зная подачу и напор
и напор  насоса при номинальном (не срезанном) рабочем колесе диаметром
насоса при номинальном (не срезанном) рабочем колесе диаметром  .
.
Из закона подобия при условии, что частота вращения и ширина колеса
и ширина колеса 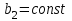
, получим:
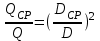 , (20.1)
, (20.1)
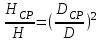 . (20.1)
. (20.1)
Экспериментальная проверка полученных равенств показывает, что для центробежных насосов, имеющих коэффициент быстроходности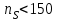 , лучшее соответствие расчетных величин
, лучшее соответствие расчетных величин  и
и  опытным данным получается при расчете величины срезки колеса по формулам:
опытным данным получается при расчете величины срезки колеса по формулам:
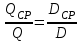 , (20.2)
, (20.2)
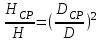 , (20.2)
, (20.2)
откуда: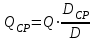 ,
, 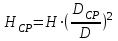 .
.
Для исследования положения режимных точек работы насоса при срезке рабочего колеса насоса рассмотрим уравнения (20.1).
Из уравнений следует, что:
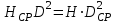 ,
, 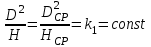

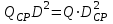 ,
,

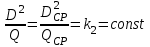
Откуда: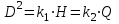 , или
, или 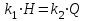 .
.
Выражая отношение коэффициентов через: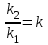 , получим:
, получим:
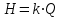 .
.
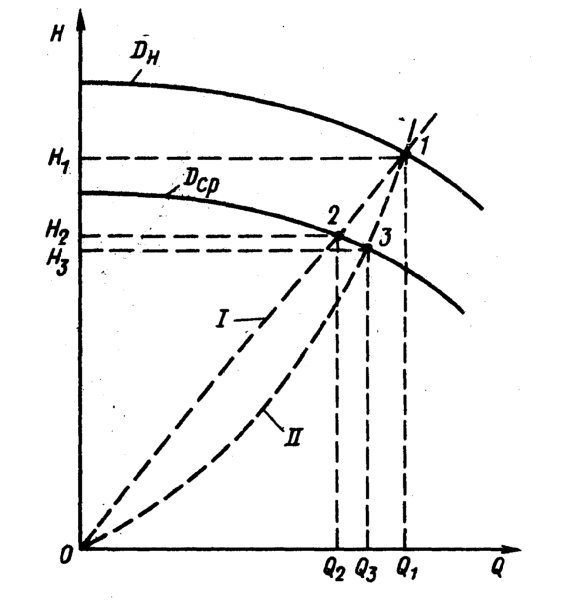
Следовательно, перемещение режимных точек в координатах при уменьшении диаметра рабочего колеса насоса происходит по прямым линиям (I), проходящим через начало координат. Таким образом точка 1 с параметрами
при уменьшении диаметра рабочего колеса насоса происходит по прямым линиям (I), проходящим через начало координат. Таким образом точка 1 с параметрами  и
и 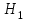 перемещается в положение 2 с параметрами
перемещается в положение 2 с параметрами 
и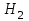 .
.
Проведем аналогичные исследования равенств (20.2):
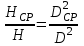
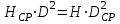
 .
.
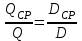
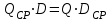
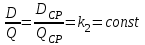
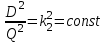 .
.
Откуда: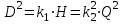 , или
, или 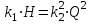
Выражая отношение коэффициентов через: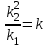 , получим:
, получим:
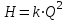 .
.
Таким образом, при расчете срезки рабочего колеса по уравнениям (20.2) режимные точки перемещаются по квадратичным параболам (II) с вершинами в начале координат, т. е. точка 1 при срезке колеса перемещается в положение 3.
Изменение КПД насоса можно рассчитать по формуле Муди:
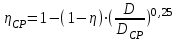 .
.
Экспериментальное исследование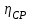 показывает, что при срезке колеса КПД изменяется незначительно в зависимости от коэффициента быстроходности.
показывает, что при срезке колеса КПД изменяется незначительно в зависимости от коэффициента быстроходности.
С достаточной степенью точности можно принять, что КПД насоса уменьшается на 1% на каждые 10% срезки колеса с коэффициентом быстроходности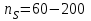 и на 1% на каждые 4% срезки при
и на 1% на каждые 4% срезки при 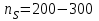 .
.
В зависимости от коэффициента быстроходности рекомендуются следующие пределы срезки колес:
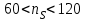 . . . . . . 20 – 15%
. . . . . . 20 – 15%
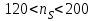 . . . . . 15 – 11%
. . . . . 15 – 11%
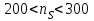 . . . . . 11 – 7 %
. . . . . 11 – 7 %
Оптимальный КПД насоса соответствует его расчетным подаче и напору
и напору 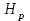 , поэтому насос следует подбирать таким образом, чтобы рабочая подача соответствовала максимальному или близкому к максимальному значению КПД. Желательно, чтобы отклонения КПД насоса, выбранного для заданного режима работы, составляли не более 5 – 10% от максимального КПД.
, поэтому насос следует подбирать таким образом, чтобы рабочая подача соответствовала максимальному или близкому к максимальному значению КПД. Желательно, чтобы отклонения КПД насоса, выбранного для заданного режима работы, составляли не более 5 – 10% от максимального КПД.
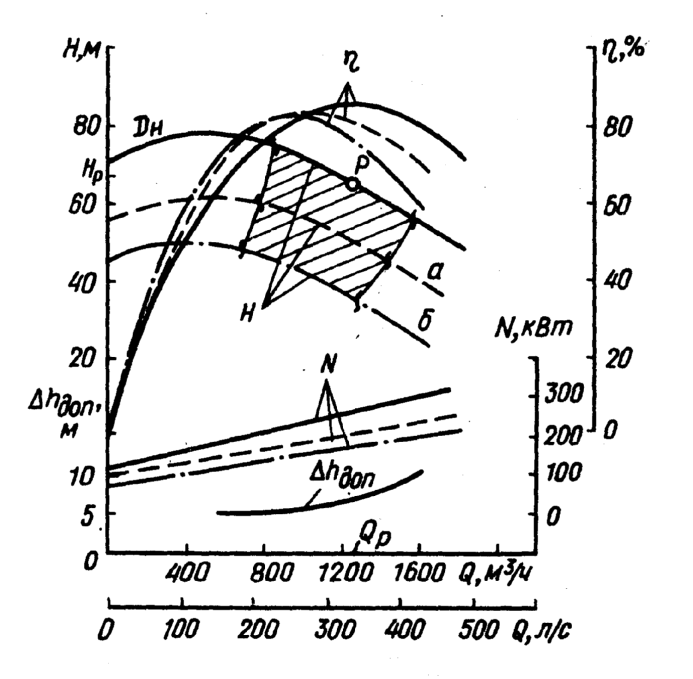
Пространство, заключенное между характеристиками при номинальном размере колеса и
при номинальном размере колеса и 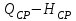 при максимально допустимой срезке колеса (линия б) и извилистыми линиями, соответствующими подачам в пределах рекомендуемых отклонений КПД, называется полем насоса – рекомендуемой областью применения насоса.
при максимально допустимой срезке колеса (линия б) и извилистыми линиями, соответствующими подачам в пределах рекомендуемых отклонений КПД, называется полем насоса – рекомендуемой областью применения насоса.
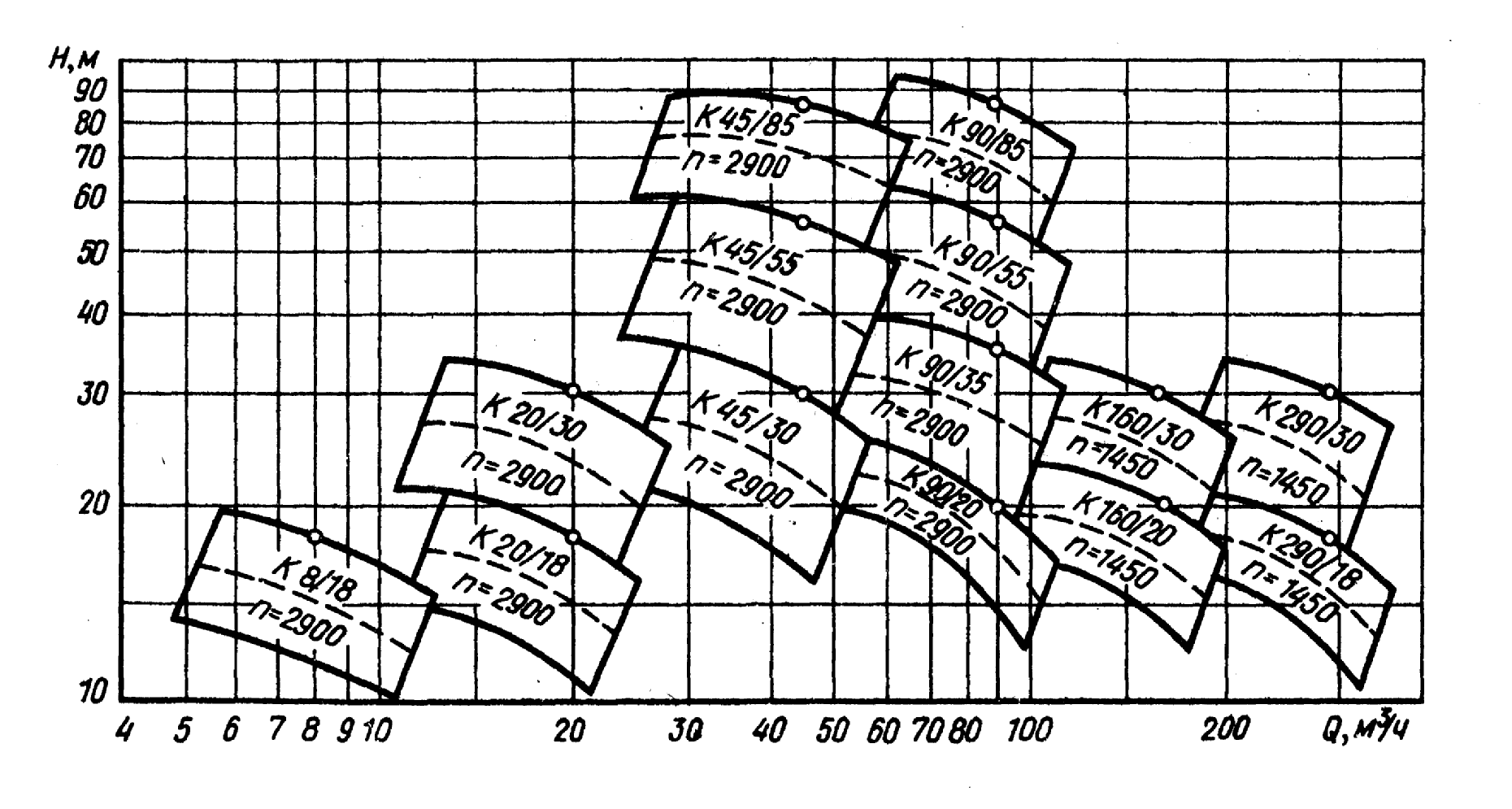
В каталогах-справочниках приводятся сводные графики полей насосов. По этим графикам удобно подбирать насос на заданный режим работы.
Сводный график полей насосов типа К приведен на рисунке:
Рассмотрим пример.
Дано:
- Технический паспорт насоса Д 320 – 50 с характеристикой и
и 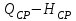 ;
;
- Номинальный диаметр рабочего колеса -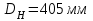 ;
;
- Рекомендуемый диаметр срезки -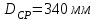 ;
;
- Режимная точка А (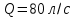 ;
; 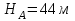 );
);
-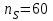 .
.
Найти:
Решение:
Воспользуемся формулами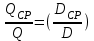 и
и  , чтобы построить параболу подобных режимов, проходящую через точку А:
, чтобы построить параболу подобных режимов, проходящую через точку А:
перепишем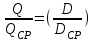 и
и 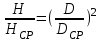 , (20.1-1)
, (20.1-1)
подставляем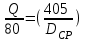 и
и 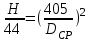 ,
,
откуда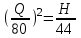 ,
,
Таким образом, получено уравнение параболы с вершиной в начале координат, проходящей через точку А, принадлежащую кривой
 и имеющую координаты
и имеющую координаты  и
и  .
.Парабола ОАi – A2 – A1 – A представляет собой геометрическое место точек, определяющих режимы насоса, подобных режиму в точке А, и называется параболой подобных режимов.
Пересчет координат точки А по закону пропорциональности для любой другой частоты вращения приведет к точкам на параболе подобных режимов.

Пересчет всякой другой точки В, С, … характеристики
 построенной при частоте вращения
построенной при частоте вращения  на частоту
на частоту  ,
,  , …
, … 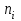 даст точки
даст точки 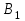 ,
, 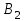 , …
, … 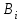 ;
; 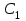 ,
, 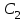 , …
, … 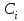 и так далее, которые расположатся соответственно на параболах
и так далее, которые расположатся соответственно на параболах 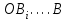 ;
; 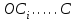 .
.Соединяя точки
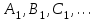 плавной кривой, получаем характеристику
плавной кривой, получаем характеристику 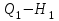 насоса для частоты вращения
насоса для частоты вращения  .
.Для характеристик
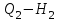 …
… 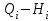 построения будут аналогичными.
построения будут аналогичными.Теоретически параболы подобных режимов являются линиями постоянного КПД.
В действительности насос не сохраняет постоянство КПД. Это связано с тем, что при изменении частоты вращения в разной степени и с разной интенсивностью проявляются потери мощности насоса (механические, объемные, гидравлические).
Отмечая на полученных характеристиках
 ,
,  …
…  точки с равными значениями КПД и соединяя их плавными кривыми, получаем так называемую универсальную характеристику.
точки с равными значениями КПД и соединяя их плавными кривыми, получаем так называемую универсальную характеристику.
Из которой видно, что максимальное значение КПД обеспечивают двигатели с частотой вращения 1450 мин-1.
-
ИЗМЕНЕНИЕ ХАРАКТЕРИСТИК НАСОСОВ ПРИ ИЗМЕНЕНИИ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ РАБОЧЕГО КОЛЕСА
Требования потребителей по подаче и напору чрезвычайно разнообразны, поэтому экономически нецелесообразно изготовлять насосы для каждого расчетного случая.
Для увеличения области применения насоса в практике проектирования и эксплуатации насосных станций применяют срезку рабочего колеса насоса, т. е. уменьшают диаметр рабочего колеса по внешнему обводу
 , сохраняя
, сохраняя 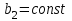 .
. Подачу
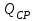 и напор
и напор 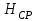 насоса, имеющего срезанное рабочее колесо диаметром
насоса, имеющего срезанное рабочее колесо диаметром 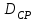 , можно определить по уравнениям закона подобия центробежных насосов:
, можно определить по уравнениям закона подобия центробежных насосов: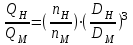 ;
; 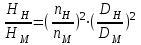 ;
; 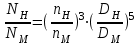 ,
,зная подачу
 и напор
и напор  насоса при номинальном (не срезанном) рабочем колесе диаметром
насоса при номинальном (не срезанном) рабочем колесе диаметром  .
.Из закона подобия при условии, что частота вращения
 и ширина колеса
и ширина колеса 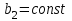
, получим:
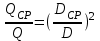 , (20.1)
, (20.1)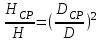 . (20.1)
. (20.1)Экспериментальная проверка полученных равенств показывает, что для центробежных насосов, имеющих коэффициент быстроходности
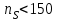 , лучшее соответствие расчетных величин
, лучшее соответствие расчетных величин  и
и  опытным данным получается при расчете величины срезки колеса по формулам:
опытным данным получается при расчете величины срезки колеса по формулам: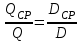 , (20.2)
, (20.2)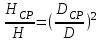 , (20.2)
, (20.2)откуда:
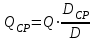 ,
, 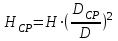 .
.Для исследования положения режимных точек работы насоса при срезке рабочего колеса насоса рассмотрим уравнения (20.1).
Из уравнений следует, что:
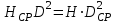 ,
, 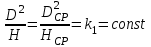

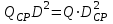 ,
,
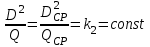
Откуда:
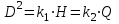 , или
, или 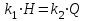 .
.Выражая отношение коэффициентов через:
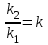 , получим:
, получим: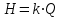 .
.
Следовательно, перемещение режимных точек в координатах
 при уменьшении диаметра рабочего колеса насоса происходит по прямым линиям (I), проходящим через начало координат. Таким образом точка 1 с параметрами
при уменьшении диаметра рабочего колеса насоса происходит по прямым линиям (I), проходящим через начало координат. Таким образом точка 1 с параметрами  и
и 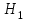 перемещается в положение 2 с параметрами
перемещается в положение 2 с параметрами 
и
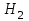 .
.Проведем аналогичные исследования равенств (20.2):
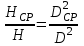
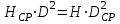
 .
.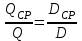
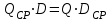
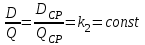
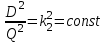 .
.Откуда:
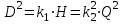 , или
, или 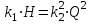
Выражая отношение коэффициентов через:
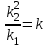 , получим:
, получим: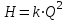 .
.Таким образом, при расчете срезки рабочего колеса по уравнениям (20.2) режимные точки перемещаются по квадратичным параболам (II) с вершинами в начале координат, т. е. точка 1 при срезке колеса перемещается в положение 3.
Изменение КПД насоса можно рассчитать по формуле Муди:
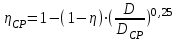 .
.Экспериментальное исследование
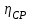 показывает, что при срезке колеса КПД изменяется незначительно в зависимости от коэффициента быстроходности.
показывает, что при срезке колеса КПД изменяется незначительно в зависимости от коэффициента быстроходности. С достаточной степенью точности можно принять, что КПД насоса уменьшается на 1% на каждые 10% срезки колеса с коэффициентом быстроходности
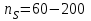 и на 1% на каждые 4% срезки при
и на 1% на каждые 4% срезки при 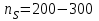 .
.В зависимости от коэффициента быстроходности рекомендуются следующие пределы срезки колес:
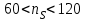 . . . . . . 20 – 15%
. . . . . . 20 – 15%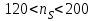 . . . . . 15 – 11%
. . . . . 15 – 11%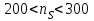 . . . . . 11 – 7 %
. . . . . 11 – 7 %Оптимальный КПД насоса соответствует его расчетным подаче
 и напору
и напору 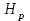 , поэтому насос следует подбирать таким образом, чтобы рабочая подача соответствовала максимальному или близкому к максимальному значению КПД. Желательно, чтобы отклонения КПД насоса, выбранного для заданного режима работы, составляли не более 5 – 10% от максимального КПД.
, поэтому насос следует подбирать таким образом, чтобы рабочая подача соответствовала максимальному или близкому к максимальному значению КПД. Желательно, чтобы отклонения КПД насоса, выбранного для заданного режима работы, составляли не более 5 – 10% от максимального КПД.
Пространство, заключенное между характеристиками
 при номинальном размере колеса и
при номинальном размере колеса и 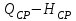 при максимально допустимой срезке колеса (линия б) и извилистыми линиями, соответствующими подачам в пределах рекомендуемых отклонений КПД, называется полем насоса – рекомендуемой областью применения насоса.
при максимально допустимой срезке колеса (линия б) и извилистыми линиями, соответствующими подачам в пределах рекомендуемых отклонений КПД, называется полем насоса – рекомендуемой областью применения насоса.
В каталогах-справочниках приводятся сводные графики полей насосов. По этим графикам удобно подбирать насос на заданный режим работы.
Сводный график полей насосов типа К приведен на рисунке:

-
РАСЧЕТ СРЕЗКИ РАБОЧЕГО КОЛЕСА ЦЕНТРОБЕЖНОГО НАСОСА
Рассмотрим пример.
Дано:
- Технический паспорт насоса Д 320 – 50 с характеристикой
 и
и 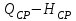 ;
;- Номинальный диаметр рабочего колеса -
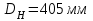 ;
;- Рекомендуемый диаметр срезки -
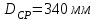 ;
;- Режимная точка А (
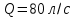 ;
; 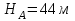 );
);-
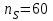 .
.Найти:
Решение:
Воспользуемся формулами
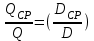 и
и  , чтобы построить параболу подобных режимов, проходящую через точку А:
, чтобы построить параболу подобных режимов, проходящую через точку А:перепишем
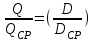 и
и 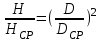 , (20.1-1)
, (20.1-1)подставляем
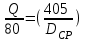 и
и 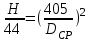 ,
,откуда
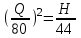 ,
,