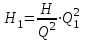ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 240
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таким образом, для более общего случая с учетом отметки установки насоса и температуры перекачиваемой жидкости высота всасывания может определяться по формуле:
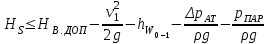 .
.Если значение величины
 в результате расчета оказывается меньше нуля, то насос должен быть установлен ниже уровня воды в приемном резервуаре, т. е. с подпором.
в результате расчета оказывается меньше нуля, то насос должен быть установлен ниже уровня воды в приемном резервуаре, т. е. с подпором.Высота всасывания насоса, являясь одним из основных параметров, определяющих компоновочное решение насосной станции или установки, в то же время не дает возможности численно оценить степень развития кавитации, а следовательно, и сравнить между собой кавитационные характеристики насосов, постоянно изменяющиеся в процессе эксплуатации.
В насосостроении для сравнения кавитационных качеств насосов, количественной оценки степени развития кавитации и анализа вопроса о выборе допустимых значений высоты всасывания пользуются критерием (параметром), который называется кавитационным запасом
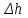 .
.Кавитационный запас представляет собой превышение механической энергии в потоке на входе в насос над давлением насыщенного пара:
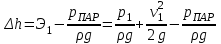 . (*)
. (*)Иногда этот параметр называется избыточным напором всасывания.
Приведем уравнение (*) к следующему виду:
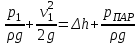 . (1*)
. (1*)Снова запишем выражение для геометрической высоты всасывания:
 (2*)
(2*)Подставим сумму
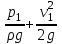 , выраженную через сумму
, выраженную через сумму 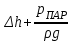 в (2*):
в (2*):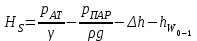 ,
,таким образом, установлена связь между геометрической высотой всасывания и кавитационным запасом.
Для каждого насоса существует некоторое минимальное значение
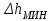 . При уменьшении кавитационного запаса ниже этого значения в насосе начинает развиваться кавитация.
. При уменьшении кавитационного запаса ниже этого значения в насосе начинает развиваться кавитация.Наименьшему значению
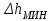 соответствует наибольшее значение геометрической высоты всасывания:
соответствует наибольшее значение геометрической высоты всасывания:
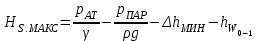 ,
,которое иногда называют критической высотой всасывания.
Для обеспечения надежной работы насоса допускаемая при эксплуатации высота всасывания
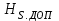 должна иметь некоторый запас, что учитывается введением коэффициента запаса:
должна иметь некоторый запас, что учитывается введением коэффициента запаса: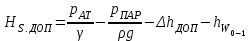 ,
,где
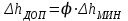 .
.В зависимости от условий работы насоса коэффициент запаса принимается равным 1,1 – 1,5.
Для определения минимального кавитационного запаса используется формула С.С. Руднева:
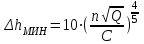 ,
,где С - постоянная, зависящая от конструктивных особенностей насоса и называемая кавитационным коэффициентом быстроходности.
-
ТЕОРЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦЕНТРОБЕЖНЫХ НАСОСОВ
Характеристикой насоса называется графически выраженная зависимость основных энергетических показателей от подачи при постоянной частоте вращения вала рабочего колеса, а также при постоянной вязкости и плотности жидкой среды на входе в насос.
Основные параметры лопастных насосов: подача, напор, мощность, КПД и частота вращения вала рабочего колеса находятся в определенной зависимости, которая лучше всего уясняется из рассмотрения характеристических кривых.
Значения напора, мощности и КПД для ряда значений подачи могут быть представлены в виде системы точек в координатах:
-
 ;
;-
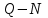 ;
;-
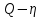 .
.Соединяя точки плавными кривыми, получаем непрерывную графическую характеристику зависимости рассматриваемых параметров от подачи насоса при постоянной частоте вращения
 .
.Основной характеристической кривой насоса является график, выражающий зависимость развиваемого насосом напора от подачи:
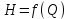 при
при 
-
СПОСОБЫ ПОЛУЧЕНИЯ ХАРАКТЕРИСТИК НАСОСОВ
При расчете режима насоса, как правило, пользуются опытными характеристиками, которые получают при испытании насосов.
При проведении опытных испытаний осуществляют измерения:
-
подачи насоса; -
напора насоса на входе и выходе из него; -
потребляемой мощности насоса; -
вакуумметрической высоты всасывания насоса.
По результатам измерений вычисляют:
-
напор, приведенный к оси насоса; -
полезную мощность при постоянной частоте вращения; -
КПД при постоянной частоте вращения.
Полученные значения напора, мощности, КПД и допустимого кавитационного запаса для ряда значений подачи представляют в виде системы точек в координатах: H, N, , hДОПи Q.
Соединяя соответствующие точки плавными линиями, получают графически выраженные зависимости рассматриваемых параметров от подачи насоса при постоянной частоте вращения для данного диаметра рабочего колеса.
Полученные кривые:
 ,
,  ,
,  ,
, 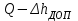 называются энергетическими характеристиками центробежного насоса и вписываются в паспорт насоса.
называются энергетическими характеристиками центробежного насоса и вписываются в паспорт насоса.Рабочие характеристики центробежного насоса представлены на рисунке:
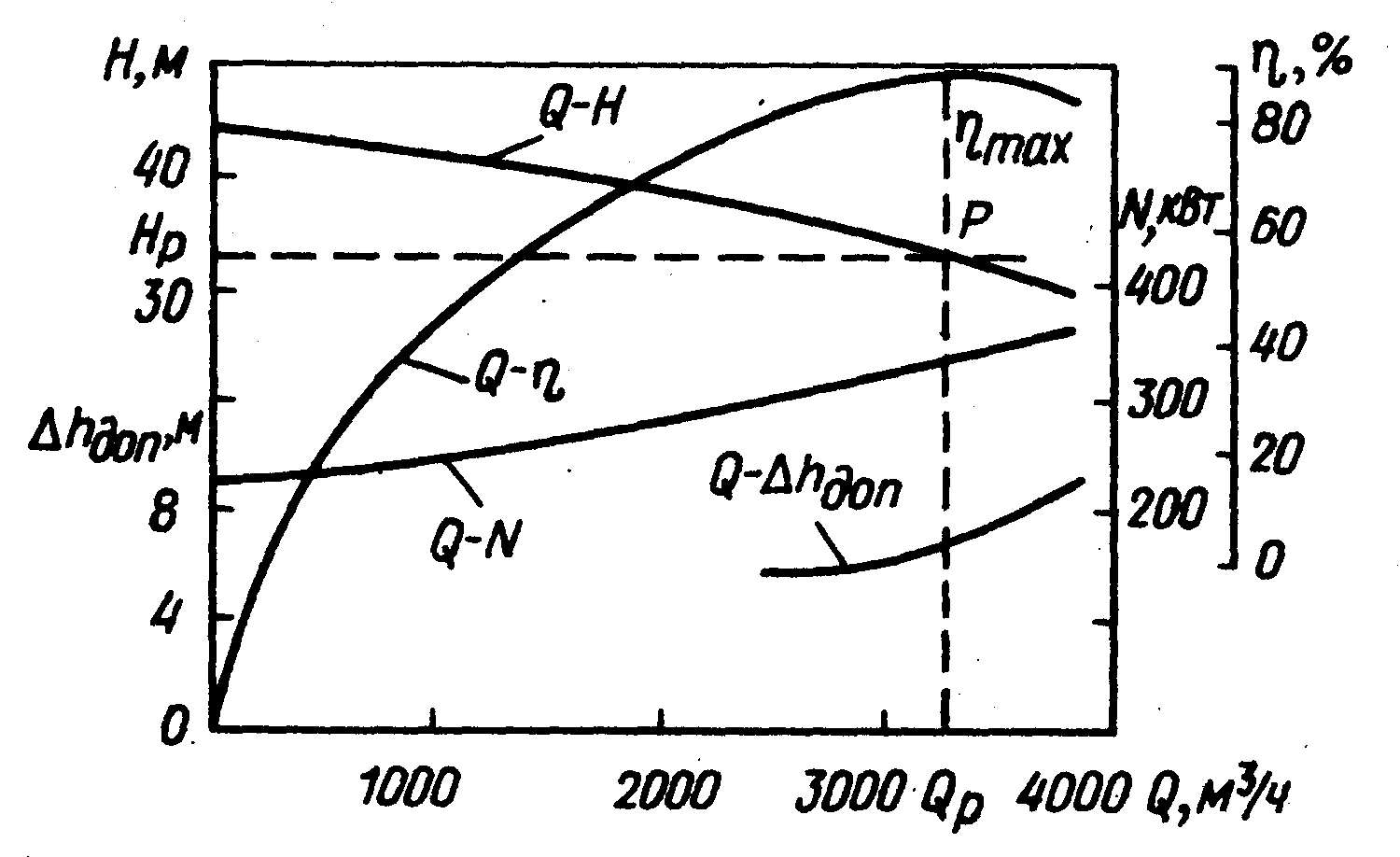
Максимальному значению КПД соответствует подача
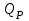 и напор
и напор 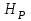 (расчетные параметры).
(расчетные параметры).Точка Р характеристики
 , отвечающая максимальному значению КПД, называется оптимальной режимной точкой.
, отвечающая максимальному значению КПД, называется оптимальной режимной точкой. Характеристика
 показывает, что с уменьшением подачи напор возрастает и при подаче, равной нулю, т. е. при закрытой задвижке на напорном трубопроводе, достигает максимального значения. Данная характеристика
показывает, что с уменьшением подачи напор возрастает и при подаче, равной нулю, т. е. при закрытой задвижке на напорном трубопроводе, достигает максимального значения. Данная характеристика 
называется стабильной (характеристика, не имеющая возрастающей ветви).
Режим работы насоса, имеющего стабильную рабочую характеристику
 , протекает устойчиво во всех точках кривой.
, протекает устойчиво во всех точках кривой.Характеристика
 насоса, в соответствии с которой, напор возрастает при начальном увеличении подачи, а затем падает, называется восходящей.
насоса, в соответствии с которой, напор возрастает при начальном увеличении подачи, а затем падает, называется восходящей. Восходящая характеристика
 представлена на рисунке:
представлена на рисунке: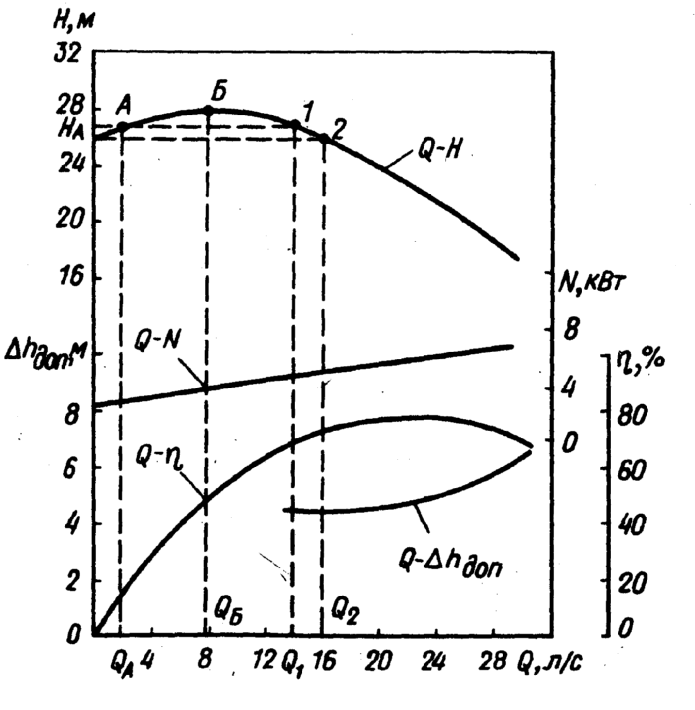
Графическая характеристика имеет восходящую ветвь от
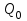 до
до 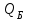 .
.Напору
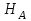 соответствуют две подачи
соответствуют две подачи 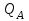 и
и 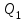 . Изменение подачи насоса наступает внезапно, сопровождается сильным шумом и гидравлическими ударами.
. Изменение подачи насоса наступает внезапно, сопровождается сильным шумом и гидравлическими ударами.Работа насоса в пределах подачи от нуля до
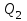 называется областью неустойчивой работы.
называется областью неустойчивой работы. Форма характеристики
 зависит от коэффициента быстроходности насоса
зависит от коэффициента быстроходности насоса  . Чем больше коэффициент быстроходности, тем круче кривая
. Чем больше коэффициент быстроходности, тем круче кривая  .
.Насосы со стабильными пологими характеристиками целесообразно применять в системах, где при постоянном напоре требуется регулирование подачи в широких пределах.
Насосы со стабильными крутопадающими характеристиками целесообразно применять в системах со значительными колебаниями напора при необходимости сохранения по возможности постоянной подачи.
Насосы с восходящими характеристиками рекомендуется применять в системах, где подача не снижается до
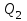 (до подачи, соответствующей напору при закрытой задвижке).
(до подачи, соответствующей напору при закрытой задвижке). -
ИЗМЕНЕНИЕ ХАРАКТЕРИСТИК НАСОСОВ ПРИ ИЗМЕНЕНИИ ЧАСТОТЫ ВРАЩЕНИЯ РАБОЧЕГО КОЛЕСА
При необходимости пересчета паспортных характеристик, установленных при частоте вращения
 на другую частоту вращения рабочего колеса
на другую частоту вращения рабочего колеса  при
при 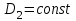 , то можно воспользоваться следующими выражениями, полученные из закона подобия центробежных насосов:
, то можно воспользоваться следующими выражениями, полученные из закона подобия центробежных насосов: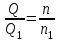 ; (19-1)
; (19-1)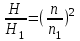 ; (19-2)
; (19-2)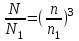 . (19-3)
. (19-3)Приведенные выше выражения называются законом пропорциональности.
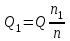 ;
;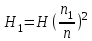 ;
;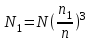 .
.Высота всасывания насоса при работе его с частотой вращения
 определяется по уравнению:
определяется по уравнению: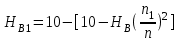 ,
,где
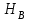 и
и 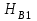 - допускаемая вакуумметрическая высота всасывания при частотах вращения
- допускаемая вакуумметрическая высота всасывания при частотах вращения  и
и  .
. Установленный закон пропорциональности позволяет по одной опытной характеристике
 построить ряд характеристик насоса в широком диапазоне изменения частоты вращения.
построить ряд характеристик насоса в широком диапазоне изменения частоты вращения.Необходимо отметить, что режим работы насоса с пониженной частотой вращения допускается всегда, но повышение частоты вращения больше чем на 10 – 15 % должно быть согласовано с заводом-изготовителем.
Исключая из уравнений (19-1) и (19-2) частоту вращения, получим:
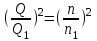 и
и 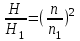 ,
,откуда:
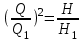 , откуда:
, откуда: