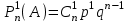
#20

*!Белгiлi бiр жағдайларда микроорганизмдер колониясының пайда болу ықтималдығы 0,7. 6 рет сынау нәтижесiнде микроорганизмдердiң 4 рет пайда болу ықтималдығын табыңыз



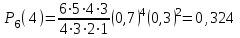
#21

*!Кездейсоқ алынған бес детальдің ішінде екеуі стандартты, әрбір детальдің стандартты болу ықтималдығы 0,9 болса, ықтималдығын табыңыз.

#22

*!Жанұяда бес бала бар. Ұл бала тууының ықтималдығы 0,5ке тең. Солардың ішінде үшеуі ұл бала болуының ықтималдығын табыңыз.

0,313 или 0,0315

#23

*! Тиын 2 рет лақтырылды. Герб және сан жағының түсу ықтималдығы неге тең? 0,25

#24

*! Тиын 2 ретлақтырылды. 2 реттедегербжағыныңтүсуықтималдығынегетең?0,25

#25

*! Тиын 2 ретлақтырылды. 2 реттедесанжағыныңтүсуықтималдығынегетең?0,25

#26

*!Пернені басқан кезде ДК-дің істен шығу ықтималдығы-0.0002 тең. 5000 таңбадан тұратын мәтінді тергенде, бірде-бір рет ақауға әкелмеу ықтималдығын табыңыз.

#27

*!Конвейер бір ауысымда 300 дана өнім қабылдайды. Конвейерде алынған өнімнің стандартты болуы ықтималдығы - 0,75. Бір ауысымдағы конвейерге стандартты өнімдердің тура 240 алу ықтималдығын табыңыз.

#28

*!Ойын сүйегі 500 рет лақтырылды. 1 санының 50 рет түсуінің ықтималдығын табыңыз.

50

#29

*!Тиынды 200 рет лақтырғанда, герб жағы 90-нан 110 ға ретке дейін түсуінің ықтималдығын табыңыз.

#30

*!Пуассонның таралу заңы деп, ықтималдығы... формуласымен анықталатын таралуды айтамыз



#31

*!Қалыпты таралғанкездейсоқшаманыңберiлгенаралыққа түсуықтималдығынесептеуформуласы



#32

*!Қалыпты таралу заңы деп, таралу тығыздығы ... формуласымен анықталатын таралуды айтамыз.



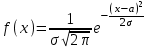
#33

*!Белгiлi бiр жағдайларда микроорганизмдер колониясының пайда болу ықтималдығы 0,7. 5рет сынау нәтижесiнде микроорганизмдердiң 3 рет пайда болу ықтималдығын табыңыз

P₅(3)=5!/3!(5-3)!*(0.7)³*(0.3)^20,3

#34

*!Егер А оқиғасы 5 сынауда 0,25 ықтималдығымен орындалса, онда осы оқиғаның 2 рет қандай пайда болу ықтималдығын табыңыз: +0,25

#35

*!Егер А оқиғасы 4 сынауда 0,25 ықтималдығымен орындалса, онда осы оқиғаның 3 рет қандай пайда болу ықтималдығын табыңыз:

---

+0,04
#36*!Нысанаға 3рет оқ атылды. Оқтың бiр рет атқандағы нысанаға тию ықтималдығы 0,25. Нысанаға бiрнеше рет атқандағы оқ тию ықтималдығын есептеу формуласын көрсетiңiз

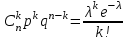;Pn(k)= 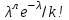мұндағы λ=np
#37

*!Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,25 тең

болса, онда А оқиғасы 1000 сынауда 250ден 300ге дейін болу ықтималдығын табу үшін қандай формулаға саласыз Муавр-Лаплас

+ ; ; ;
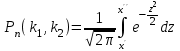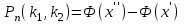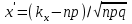
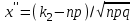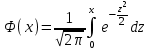
#38

*!Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,002 тең

болса, онда А оқиғасы 1000 сынауда 3 рет пайда болу ықтималдығын табу үшін қандай формулаға саласыз: : Пуассон

+
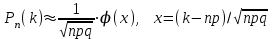
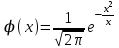
#39

*!Сапасыз өнімді шығару ықтималдығы 0,02. Шығарылған 2500 өнімнің ішінде 100 өнімнің сапасыз болу ықтималдығы табу үшін, қандай формулаға саласыз: +Pn(k)= 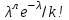; мұндағы λ=np
#40

*!Сапасыз өнімді шығару ықтималдығы 0,02. Шығарылған 2500 өнімнің ішінде 50 өнімнің сапасыз болу ықтималдығы табу үшін, қандай формулаға саласыз: +Pn(k)= 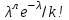мұндағы λ=np.
#41

*! Егер А оқиғасының пайда болу ықтималдығы әрбір сынауда 0,25 тең

болса, онда А оқиғасы 1000 сынауда 250ден 300ге дейін болу ықтималдығын табу үшін қандай формулаға саласыз: + ; ; ;
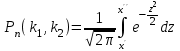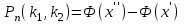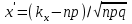
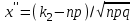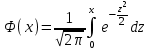
#42

*! Машинаның бір сағат ішінде жұмысшының назарын аудару ықтималдығы - 0,6 тең. Машиналардағы ақауларға байланысты, бір сағат ішінде жұмысшы өзі басқаратын төрт машинаның кез-келгенін талап етеді деген ықтималдығын табу үшін қандай формулаға саласыз:

---

;
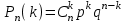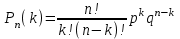
#43

*!10 теледидардан тұратын топтамада 3 істен шыққан теледидар бар. Осы партиядан 2 теледидар кездейсоқ таңдалады. Таңдалған екеуінің де ақауы болуының ықтималдығын табыңыз +1.89 немесе 1/15

#44

*!Біреу екі билетті сатып алды. Ең болмағанда бір билетті ұтып алу мүмкіндігі - 0,19. Бір лотерея билетін ұтып алу ықтималдығы қандай?

#45

*!Студенттер 6 күнде 4 емтихан тапсыруы керек. Емтихандарды тапсыру кестесін неше әдіспен құруға болады?30
#46

*!Бөлшекті қысқартыңыз:

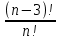
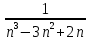немесе n!(n-3)/n!=n-3

#47

*!Үздiксiз кездейсоқ шаманың берiлген аралыққа түсу ықтималдығын есептеу формуласы: +

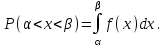
47. Бірінші студенттің сабаққа кешігіп келу ықтималдығы 0,2-ге, ал екінші студент үшін 0,4. Екі студенттің бірге сабаққа кешігіп келу ықтималдығы нешеге тең: 0,08
#48»

*!Пуассон формуласы ... ықтималдығын есептейдi:

+Сынаулар саны жеткiлiктi көп болған жағдайдағы және оқиғаның пайда болу ықтималдығының жеткiлiктi аз болған жағдайдағы оқиғаның k рет пайда болу
#49

_{*!Бернулли формуласы қандай ықтималдықтарды есептейдi}:Сызықтық біртекті емес дифференциалдық теңдеуді шешудің тұрақтыны вариациялау әдісі

+n рет сынау жасағандағы оқиғаның k рет пайда болу ықтималдығын
#50

*!Мерген 10 жағдайдың 8-де орташа нысанаға дәл тигізеді, 3 рет атқанда 2 рет дәл тигізуінің ықтималдығы: 0,384

#51

*!Лотереядан ұту ықтималдығы - 0,3. Сатып алынған 100 билеттің 30-ында ұтысқа ие болу ықтималдығы:

#52

*! Лаплас формуласын қолдану ...негізделген:

Егер әрбір тәжірибеде А оқиғасының пайда болу р ықтималдығы тұрақты және нөл мен бірден өзгеше болса, онда ықтималдығы n тәжірибе жүргізгенде А оқиғасы k рет пайда болады, (n үлкен болған сайын нақты) жуық түрде функцияның мәні
#53

*!Бернулли формуласының орнына Лаплас формуласын қолданудың артықшылығы

: егер n тым улкен болса, р аз болганда накты жауапка жакын Лаплас формуласымен аныктай аламыз

---

#54

*! Лапластың интегралдық теремасын қолдану ...негізделген:

---

+оқиғаның n сынауда k1-ден k2-ге дейiн пайда болуын. Немесе Егер әрбір тәжірибеде А оқиғасының пайда болу р ықтималдығы тұрақты және нөл мен бірден өзгеше болса, онда ықтималдығы n тәжірибе жүргізгенде А оқиғасы k1 - ден k2-ге дейін пайда болады, жуық түрде анықталған интегралға тең:
#55

*!Пуассонның таралу заңы деп таралу деп аталады, оның ықтималдығы формуламен анықталатын таралуды айтамыз

Бұл формула (n үлкен) және (р аз) сирек оқиғалар үшін Пуассонның таралу заңы деп аталады

#56

*!Таралудың қалыпты заңы деп - ықтималдылық тығыздығымн анықталатын таралуды айтамыз.


#1

*!Х кездейсоқ шамасы (0,1) аралығында f(х)=2х+1 тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 7/6

#2

Орта квадраттық ауытқуды есептеу формуласы:

#3

*! Х үзiлiссiз кездейсоқ шаманың қабылдайтын мүмкін мәндері Ох осінің бойында жатса, математикалық күтімнің формуласы: +M(x)=

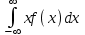
3.

#4

*! Х кездейсоқ шамасы (0,1) аралығында f(х)=3х² тығыздығымен берiлген, аралықтың сыртында f(х)=0 . Х кездейсоқ шамасының математикалық күтiмiн табыңыз: 3/4

#5

*! М(С)=С нені білдіреді:

Тұрақты шаманың математикалық күтімі өзіне тең, яғни С тұрақты болса: М(С)=C.

#6

*!М(СХ)=СМ(Х) нені білдіреді: Тұрақты шаманы математикалық күтімнің алдына шығаруға болады:

#7

*! М(ХУ)=М(Х)М(У) нені білдіреді: Екі тәуелсіз кездейсоқ шама көбейтіндісінің математикалық күтімі олардың математикалық күтімдерінің көбейтіндісіне тең

#8

*! М(Х+У)=М(Х)+М(У) нені білдіреді: Екі тәуелсіз кездейсоқ шаманың қосындысының математикалық күтімі, қосылғаштардың математикалық күтімдерінің қосындысына тең

#9*! М(Х+У+Z)=М(Х)+М(У)+M(Z) нені білдіреді: + Бірнеше кездейсоқ шамалардың қосындысын математикалық өңдеу олардың математикалық өңдеу жиынтығына тең.

---

Смотрите также файлы

• Е. Е. Складнова, Г. А. Воробьёва ккоон.pdf

• Темы рефератов по дисциплине Социальная политика государства.docx

• Литература физика количество и доля сдававших егэ по предмету.docx

• Обобщающее повторение Дальний Восток Какой субъект рф не входит в состав Дальневосточного района.docx

• Тематическое планирование 2 класс 34 час Тематические блоки, темы Номер и тема урока Количество часов Основное содержание Методы и формы организации обучения.doc