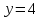Файл: Сені олынан брі келеді, тек зіе сен (кейбір сратарды жауабын таба алмадым, барымша істедім) жне матрицалары берілген.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 105
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
:
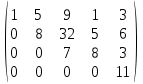 , демек, берілген жүйенің анықтауышы нольге тең
, демек, берілген жүйенің анықтауышы нольге тең
#74. теңдеулер жүйесінің анықтауышы
теңдеулер жүйесінің анықтауышы
* =3+0-8-6-0+10= -1
=3+0-8-6-0+10= -1
#75.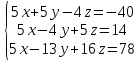 Теңдеулер жүйесін Гаусс әдісімен шешіңіз. x(y+z) өрнегінің мәні
Теңдеулер жүйесін Гаусс әдісімен шешіңіз. x(y+z) өрнегінің мәні
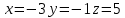 -12
-12
#76.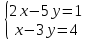 теңдеулер жүйесінің матрицасына кері матица:
теңдеулер жүйесінің матрицасына кері матица:
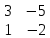
#77.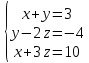 теңдеулер жүйесін Крамер әдісімен шешіңіз. x+y+z өрнегінің мәні:
теңдеулер жүйесін Крамер әдісімен шешіңіз. x+y+z өрнегінің мәні:
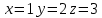 1+2+3= 6
1+2+3= 6
#78. Сызықты теңдеулер жүйесін шешудің Гаусс әдісі екі жолдан тұрады:
тура және кері
#79. Сызықты теңдеулерді шешудің Гаусс әдісі бойынша тура жолдың нәтижесінде:
#80. Сызықты теңдеулерді шешудің Гаусс әдісі бойынша кері жолдың нәтижесінде:
#81. Гаусс әдісі келесі жүйелерді шешуге қолданылады:
Сызыктық теңдеулер жүйесін
#82. Сызықты теңдеулер жүйесін шешудің Гаусс әдісінің басқаша атауы
Жордан-Гаусс әдісі, Баспалдақ түрге келтіру әдісі
#83. i-ші түрдегі бактерия күніне орта есеппен сij j-ші субстратпен тағамданады. i-ші түр үшін сi=(ci1,ci2,ci3) тағамдану векторын анықтаңыз. Мұндағы с1=(1,1,1), с2=(1,2,3) и с3=(1,3,5).
Вектор өткен жоқпыз
#84. анықтауышы
анықтауышы 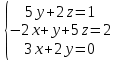
detA= 0+75-8-6-0-0= 61
Анықталған интеграл. 28 тест
#1.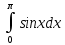 интегралы қандай әдiспен есептеледi: Тікелей интегралдау әдісімен
интегралы қандай әдiспен есептеледi: Тікелей интегралдау әдісімен
#2.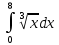 интегралы қандай әдiспен есептеледi:
интегралы қандай әдiспен есептеледi:
12, Тікелей интегралдау әдісімен
#3.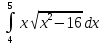 интегралы қандай әдiспен есептеледi:
интегралы қандай әдiспен есептеледi:
9, Жаңа айнымалы енгізу әдісімен
#4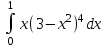 интегралы қандай әдiспен есептеледi:
интегралы қандай әдiспен есептеледi:
211/10 н/е 21,1; Жаңа айнымалы енгізу әдісімен
#5.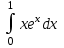 интегралы қандай әдiспен есептеледi: Бөліктеп интегралдау әдісімен.
интегралы қандай әдiспен есептеледi: Бөліктеп интегралдау әдісімен.
#6.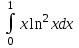 интегралы қандай әдiспен есептеледi:Бөліктеп интегралдау әдісімен.
интегралы қандай әдiспен есептеледi:Бөліктеп интегралдау әдісімен.
#7. Анықталған интегралды есептеуде қолданылатын формула
Жауабы: Ньютон-Лейбниц формуласы: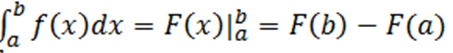
#8. Анықталған интегралдың шектерін алмастырғанда интегралдың таңбасы ... өзгереді
Қарама-қарсы таңбаға
#9. Интегралдың шектері бірдей болса, онда анықталған интеграл тең болады.
∫_a^a▒〖f(x)dx=0〗нөлге тең болады
#10.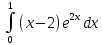 интегралындағы u мен dv дұрыс таңдаңыз:U=
интегралындағы u мен dv дұрыс таңдаңыз:U=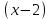 , dv=e²ˣdx
, dv=e²ˣdx
#11.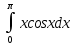 интегралындағы u мен dv дұрыс таңдаңыз
интегралындағы u мен dv дұрыс таңдаңыз
U=x, dv=cos(x)*dx. Есеп мәні=-2.
#12. Анықталған интегралдың қасиеті
1)
4)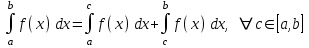 , 5)
, 5)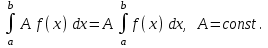
6)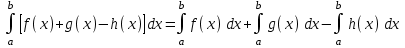 . 7)
. 7)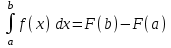
8)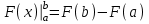
#13. Анықталған интегралдың қасиеті
#14. Анықталған интегралдың қасиеті
#15. Анықталған интегралдың қасиеті
#16. Егер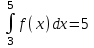 және
және 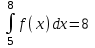 болса, онда мына интегралды
болса, онда мына интегралды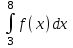 есептеңіз: 13
есептеңіз: 13
#17. Егер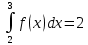 және
және 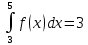 болса, онда мына интегралды
болса, онда мына интегралды 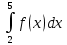 есептеңіз: 5
есептеңіз: 5
#18. Анықталған интегралда бөліктепинтегралдау әдісінің формуласы
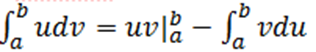
#19. Интегралды есептеңіз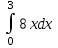 :
:
36
#20. Интегралды есептеңіз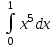
1/6
#21. Интегралды есептеңіз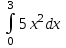
45
#22. Интегралды есептеңіз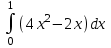
1/3
#23. Интегралды есептеңіз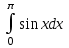
2
#24. Интегралды есептеңіз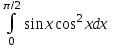
cos²
#25. Интегралды есептеңіз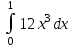 :
:
3
#26.Интегралды есептеңіз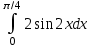
1
#27.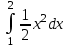 .Интегралды есептеңіз
.Интегралды есептеңіз
7/6
#28.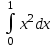 Интегралды есептеңіз
Интегралды есептеңіз
1/3
Анықталған интегралдың қолданылуы. 36 тест
#1
*! Меншіксіз интегралды есептеу формуласы
#2
*! Меншіксіз интегралды көрсетіңіз
#3
*!y=f(x),a≤х≤b теңдеуі арқылы берілген қисықтың доғасының ұзындығының формуласы
#4
*! 0≤y≤f(x),a≤x≤b қисық сызықты трапециясын Ох осінің айналасында айналдыру арқылы алынған дененің көлемі
#5
*! 0≤x≤φ(y),c≤y≤d қисық сызықты трапециясын Оу осінің айналасында айналдыру арқылы алынған дененің көлемі
118.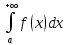 меншіксіз интегралы жинақты болады, егер
меншіксіз интегралы жинақты болады, егер
+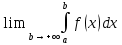 шегі бар және ақырлы
шегі бар және ақырлы
119.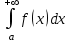 меншіксіз интегралы жинақсыз, егер
меншіксіз интегралы жинақсыз, егер
*+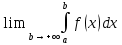 ақырсыз
ақырсыз
120. Айналу дененің көлемі

121.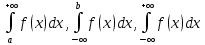 түрінде берілген интегралдың аталуы
түрінде берілген интегралдың аталуы
*+меншіксіз интеграл
122.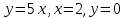 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы
+10
123. y=3x-1, x=2, x=4, y=0 түзумен шектелген фигураның ауданы
+16
124.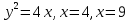 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы
+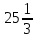
125.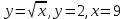 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы
+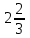
126.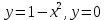 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы
+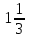
127.y=sinx,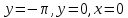 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы
+2
128. у=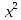 , у=2х, y=x түзумен шектелген фигураның ауданы
, у=2х, y=x түзумен шектелген фигураның ауданы
+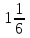
129. y=x3, x=0, y=8 түзулерімен шектелген фигураны Ох осінен айналдырғаннан шыққан дене көлемі
+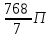
130. xy=6, x=1, x=4, y= түзулерімен шектелген фигураны Oyосінен айналдырғаннан шыққан дене көлемі
+36П
131. xy=6, x=1, x=4, y=0 түзулерімен шектелген фигураны Ох осінен айналдырғаннан шыққан дене көлемі
+27П
132. x=0 және x=3 түзулерімен шектелген y=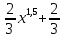 қисық доғасының ұзындығы
қисық доғасының ұзындығы
+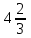
133.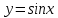 Ох осінен айналдырғаннан шыққан дене көлемі
Ох осінен айналдырғаннан шыққан дене көлемі
+
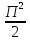
134. Меншіксіз интегралды есептеңіз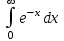
+1
135. Қисықтармен шектелген фигураның ауданы: *+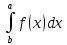
136. Қисық доғасының ұзындығы: *+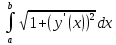
137.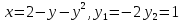 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы
+4,5
138.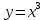 ,
, 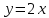 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы
+2
139.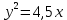 ,
, 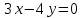 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы
+8
140.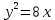 , 2
, 2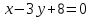 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы
+
141.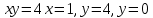 түзулерімен шектелген айналу денесінің көлемі
түзулерімен шектелген айналу денесінің көлемі
+12П
142. Меншіксіз интегралды есептеңіз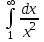
+1
143. y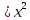 ,
, 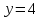
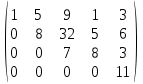 , демек, берілген жүйенің анықтауышы нольге тең
, демек, берілген жүйенің анықтауышы нольге тең#74.
 теңдеулер жүйесінің анықтауышы
теңдеулер жүйесінің анықтауышы*
 =3+0-8-6-0+10= -1
=3+0-8-6-0+10= -1#75.
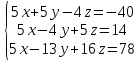 Теңдеулер жүйесін Гаусс әдісімен шешіңіз. x(y+z) өрнегінің мәні
Теңдеулер жүйесін Гаусс әдісімен шешіңіз. x(y+z) өрнегінің мәні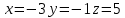 -12
-12#76.
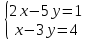 теңдеулер жүйесінің матрицасына кері матица:
теңдеулер жүйесінің матрицасына кері матица: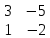
#77.
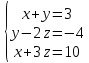 теңдеулер жүйесін Крамер әдісімен шешіңіз. x+y+z өрнегінің мәні:
теңдеулер жүйесін Крамер әдісімен шешіңіз. x+y+z өрнегінің мәні: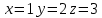 1+2+3= 6
1+2+3= 6#78. Сызықты теңдеулер жүйесін шешудің Гаусс әдісі екі жолдан тұрады:
тура және кері
#79. Сызықты теңдеулерді шешудің Гаусс әдісі бойынша тура жолдың нәтижесінде:
#80. Сызықты теңдеулерді шешудің Гаусс әдісі бойынша кері жолдың нәтижесінде:
#81. Гаусс әдісі келесі жүйелерді шешуге қолданылады:
Сызыктық теңдеулер жүйесін
#82. Сызықты теңдеулер жүйесін шешудің Гаусс әдісінің басқаша атауы
Жордан-Гаусс әдісі, Баспалдақ түрге келтіру әдісі
#83. i-ші түрдегі бактерия күніне орта есеппен сij j-ші субстратпен тағамданады. i-ші түр үшін сi=(ci1,ci2,ci3) тағамдану векторын анықтаңыз. Мұндағы с1=(1,1,1), с2=(1,2,3) и с3=(1,3,5).
Вектор өткен жоқпыз
#84.
 анықтауышы
анықтауышы 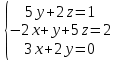
detA= 0+75-8-6-0-0= 61
Анықталған интеграл. 28 тест
#1.
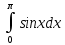 интегралы қандай әдiспен есептеледi: Тікелей интегралдау әдісімен
интегралы қандай әдiспен есептеледi: Тікелей интегралдау әдісімен#2.
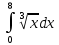 интегралы қандай әдiспен есептеледi:
интегралы қандай әдiспен есептеледi:12, Тікелей интегралдау әдісімен
#3.
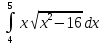 интегралы қандай әдiспен есептеледi:
интегралы қандай әдiспен есептеледi:
9, Жаңа айнымалы енгізу әдісімен
#4
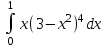 интегралы қандай әдiспен есептеледi:
интегралы қандай әдiспен есептеледi: 211/10 н/е 21,1; Жаңа айнымалы енгізу әдісімен
#5.
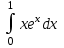 интегралы қандай әдiспен есептеледi: Бөліктеп интегралдау әдісімен.
интегралы қандай әдiспен есептеледi: Бөліктеп интегралдау әдісімен.#6.
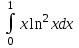 интегралы қандай әдiспен есептеледi:Бөліктеп интегралдау әдісімен.
интегралы қандай әдiспен есептеледi:Бөліктеп интегралдау әдісімен.#7. Анықталған интегралды есептеуде қолданылатын формула
Жауабы: Ньютон-Лейбниц формуласы:
#8. Анықталған интегралдың шектерін алмастырғанда интегралдың таңбасы ... өзгереді
Қарама-қарсы таңбаға
#9. Интегралдың шектері бірдей болса, онда анықталған интеграл тең болады.
∫_a^a▒〖f(x)dx=0〗нөлге тең болады
#10.
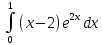 интегралындағы u мен dv дұрыс таңдаңыз:U=
интегралындағы u мен dv дұрыс таңдаңыз:U=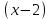 , dv=e²ˣdx
, dv=e²ˣdx #11.
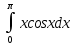 интегралындағы u мен dv дұрыс таңдаңыз
интегралындағы u мен dv дұрыс таңдаңыз U=x, dv=cos(x)*dx. Есеп мәні=-2.
#12. Анықталған интегралдың қасиеті
1)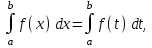 2)
2)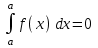 , 3)
, 3)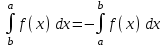 ,
,
4)
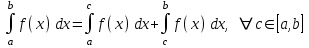 , 5)
, 5)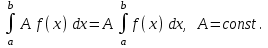
6)
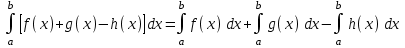 . 7)
. 7)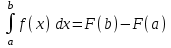
8)
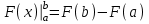
#13. Анықталған интегралдың қасиеті
#14. Анықталған интегралдың қасиеті
#15. Анықталған интегралдың қасиеті
#16. Егер
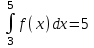 және
және 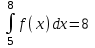 болса, онда мына интегралды
болса, онда мына интегралды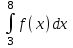 есептеңіз: 13
есептеңіз: 13#17. Егер
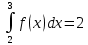 және
және 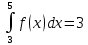 болса, онда мына интегралды
болса, онда мына интегралды 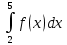 есептеңіз: 5
есептеңіз: 5#18. Анықталған интегралда бөліктепинтегралдау әдісінің формуласы
#19. Интегралды есептеңіз
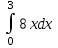 :
:36
#20. Интегралды есептеңіз
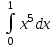
1/6
#21. Интегралды есептеңіз
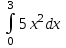
45
#22. Интегралды есептеңіз
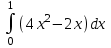
1/3
#23. Интегралды есептеңіз
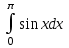
2
#24. Интегралды есептеңіз
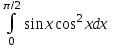
cos²
#25. Интегралды есептеңіз
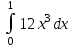 :
:3
#26.Интегралды есептеңіз
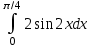
1
#27.
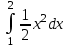 .Интегралды есептеңіз
.Интегралды есептеңіз7/6
#28.
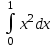 Интегралды есептеңіз
Интегралды есептеңіз1/3
Анықталған интегралдың қолданылуы. 36 тест
#1
*! Меншіксіз интегралды есептеу формуласы
#2
*! Меншіксіз интегралды көрсетіңіз
#3
*!y=f(x),a≤х≤b теңдеуі арқылы берілген қисықтың доғасының ұзындығының формуласы
#4
*! 0≤y≤f(x),a≤x≤b қисық сызықты трапециясын Ох осінің айналасында айналдыру арқылы алынған дененің көлемі
#5
*! 0≤x≤φ(y),c≤y≤d қисық сызықты трапециясын Оу осінің айналасында айналдыру арқылы алынған дененің көлемі
118.
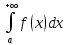 меншіксіз интегралы жинақты болады, егер
меншіксіз интегралы жинақты болады, егер+
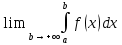 шегі бар және ақырлы
шегі бар және ақырлы119.
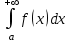 меншіксіз интегралы жинақсыз, егер
меншіксіз интегралы жинақсыз, егер*+
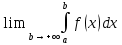 ақырсыз
ақырсыз120. Айналу дененің көлемі
121.
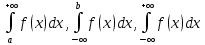 түрінде берілген интегралдың аталуы
түрінде берілген интегралдың аталуы*+меншіксіз интеграл
122.
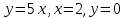 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы+10
123. y=3x-1, x=2, x=4, y=0 түзумен шектелген фигураның ауданы
+16
124.
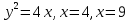 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы+
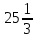
125.
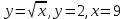 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы+
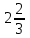
126.
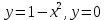 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы+
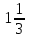
127.y=sinx,
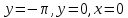 түзумен шектелген фигураның ауданы
түзумен шектелген фигураның ауданы+2
128. у=
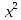 , у=2х, y=x түзумен шектелген фигураның ауданы
, у=2х, y=x түзумен шектелген фигураның ауданы
+
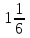
129. y=x3, x=0, y=8 түзулерімен шектелген фигураны Ох осінен айналдырғаннан шыққан дене көлемі
+
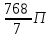
130. xy=6, x=1, x=4, y= түзулерімен шектелген фигураны Oyосінен айналдырғаннан шыққан дене көлемі
+36П
131. xy=6, x=1, x=4, y=0 түзулерімен шектелген фигураны Ох осінен айналдырғаннан шыққан дене көлемі
+27П
132. x=0 және x=3 түзулерімен шектелген y=
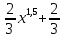 қисық доғасының ұзындығы
қисық доғасының ұзындығы +
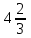
133.
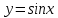 Ох осінен айналдырғаннан шыққан дене көлемі
Ох осінен айналдырғаннан шыққан дене көлемі+

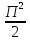
134. Меншіксіз интегралды есептеңіз
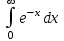
+1
135. Қисықтармен шектелген фигураның ауданы: *+
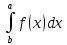
136. Қисық доғасының ұзындығы: *+
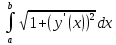
137.
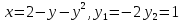 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы +4,5
138.
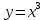 ,
, 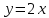 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы +2
139.
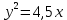 ,
, 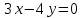 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы +8
140.
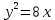 , 2
, 2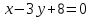 түзулерімен шектелген фигураның ауданы
түзулерімен шектелген фигураның ауданы +

141.
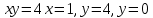 түзулерімен шектелген айналу денесінің көлемі
түзулерімен шектелген айналу денесінің көлемі +12П
142. Меншіксіз интегралды есептеңіз
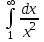
+1
143. y
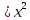 ,
,